【CCF-CSP】 202309-3 梯度求解

思路:
将表达式整理成只有目标求导变量的无括号加法表达式,其他变量均代入其值,然后利用最简单的求导公式,求出最终值。
样例1
x1 x1 x1 * x2 + *转换成 x1*x1*x1+x1*x2
若求导x1,则只留下x1,变为 x1*x1*x1+x1*3
求导完就是 3*x1*x1+3更一般的,我们可以只记录表达式的系数和指数,那么我们要将每个运算数转换为一元表达式
x1*x1*x1+x1*3转换为
指数1 系数3
指数3 系数1求导之后为
指数0 系数3*1
指数2 系数1*3对于+运算和-运算,对最终表达式就是直接相加和相减就好了,对*运算,我们要将两个表达式进行乘法运算,指数相加,系数相乘
样例1x1*x1
转换为(指数1 系数1)*(指数1 系数1)=(指数2 系数1)
x1*x1+x2
转换为(指数2 系数1)+(指数0 系数x2)=(指数0 系数x2 指数2 系数1)
代码:
#include <bits/stdc++.h>
#define N 105
using namespace std;
typedef long long ll;
const int mod=1e9+7;int n,m;
ll a[N],k;
string str,s;
vector<string> ve;
stack<map<ll,ll> > st;//记录运算数的一元表达式的系数和指数int main(){cin>>n>>m;getchar();getline(cin,str);stringstream ss(str);while(ss>>s){//所有的运算符和运算数ve.push_back(s);}for(int t=0;t<m;t++){cin>>k;str="x"+to_string(k);//求导变量for(int i=1;i<=n;i++) cin>>a[i];for(int i=0;i<ve.size();i++){s=ve[i];if(s=="+"||s=="-"||s=="*"){//运算符map<ll,ll> mp2=st.top(); st.pop();map<ll,ll> mp1=st.top(); st.pop();map<ll,ll> mp;if(s=="+"){//加法mp=mp1;for(map<ll,ll>::iterator it=mp2.begin();it!=mp2.end();it++){mp[it->first]+=it->second;mp[it->first]%=mod;}}else if(s=="-"){//减法mp=mp1;for(map<ll,ll>::iterator it=mp2.begin();it!=mp2.end();it++){mp[it->first]-=it->second;mp[it->first]%=mod;}}else{//乘法for(map<ll,ll>::iterator it1=mp1.begin();it1!=mp1.end();it1++){for(map<ll,ll>::iterator it2=mp2.begin();it2!=mp2.end();it2++){mp[it1->first+it2->first]+=it1->second*it2->second;mp[it1->first+it2->first]%=mod;}}}mp1.clear(); mp2.clear();st.push(mp);}else if(s==str){//是求导变量,保留map<ll,ll> mp;mp[1]=1;st.push(mp);}else if(s[0]=='x'){//是其他变量,则代入其值int d=stod(s.substr(1));map<ll,ll> mp;mp[0]=a[d]%mod;st.push(mp);}else{//是数字ll d=stol(s);map<ll,ll> mp;mp[0]=d%mod;st.push(mp);}}map<ll,ll> mp=st.top(); st.pop();//获得结果的一元表达式ll ans=0,fac=1,pree=0;for(map<ll,ll>::iterator it=mp.begin();it!=mp.end();it++){ll e=it->first,c=it->second;for(int i=pree+1;i<e;i++) fac=fac*a[k]%mod; pree=e==0?0:e-1;ans=(ans+c*e*fac)%mod;//简单求导公式}cout<<(ans+mod)%mod<<endl;mp.clear();}return 0;
}相关文章:

【CCF-CSP】 202309-3 梯度求解
思路: 将表达式整理成只有目标求导变量的无括号加法表达式,其他变量均代入其值,然后利用最简单的求导公式,求出最终值。 样例1 x1 x1 x1 * x2 *转换成 x1*x1*x1x1*x2 若求导x1,则只留下x1,变为 x1*x1*x1…...
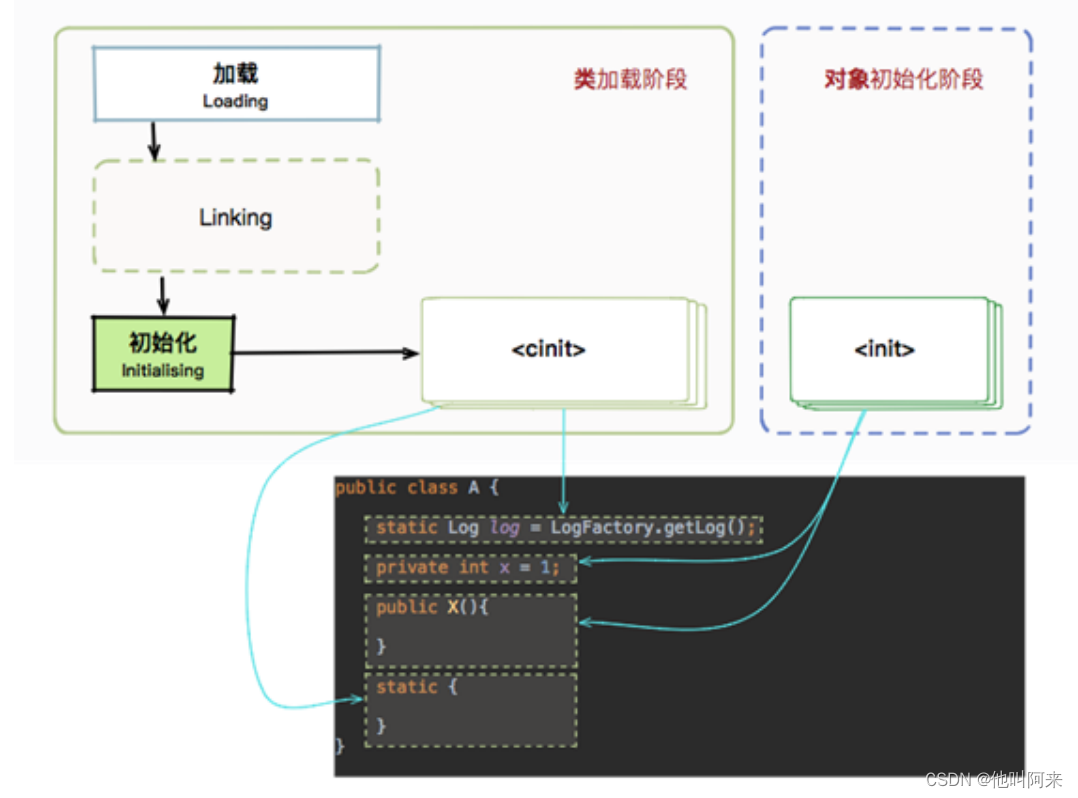
jvm的类加载
文章目录 概要加载类加载器分类双亲委派模型自定义加载器 验证准备解析初始化<cinit>与<init> 概要 jvm运行时的整体结构如下 一个Car类,类跟Car对象的转换过程如下: 加载后的class类信息存放于方法区;ClassLoader只负责clas…...

2024年汉字小达人活动4个多月开赛:18道历年选择题和答案、解析
根据近年的安排,2024年第11届汉字小达人比赛还有4个多月就启动,那么孩子们如何利用这段时间有条不紊地备考呢?我的建议是两手准备:①把小学1-5年级的语文课本上的知识点熟悉,重点是字、词、成语、古诗。②把历年真题刷…...

群晖安装青龙脚本
青龙定时任务管理面板,支持 Python3、JavaScript、Shell、Typescript 这几种环境,通过它可以方便的管理和运行定时任务(在某个时间执行一段代码),并且只需简单的配置,就可以在各个平台收到任务执行的结果通…...

【机器学习系列】使用高斯贝叶斯模型进行数据分类的完整流程
目录 一、导入数据 二、选择特征 三、十折交叉验证 四、划分训练集和测试集 五、训练高斯贝叶斯模型 六、预测测试集 七、查看训练集和测试集上的分数 八、查看混合矩阵 九、输出评估指标 一、导入数据 # 根据商户数据预测其是否续约案例 import pandas #读取数据到 da…...

Python中的单例模式:原理、实现与应用
Python中的单例模式:原理、实现与应用 一、引言 在软件开发中,设计模式是一种用于解决常见问题的最佳实践。单例模式(Singleton Pattern)是这些设计模式中的一种,它确保一个类仅有一个实例,并提供一个全局…...

Linux基础(六):Linux 系统上 C 程序的编译与调试
本篇博客详细分析,Linux平台上C程序的编译过程与调试方法,这也是我们后续程序开发的基础。 目录 一、第一个hello world程序 1.1 创建.c文件 1.2 编译链接 运行可执行程序 二、编译链接过程 2.1 预编译阶段 2.2 编译阶段 2.3 汇编阶段 2.4 链…...

移动硬盘难题:不显示容量与无法访问的解决策略
在使用移动硬盘的过程中,有时会遇到一些棘手的问题,比如移动硬盘不显示容量且无法访问。这种情况让人十分头疼,因为它不仅影响了数据的正常使用,还可能导致重要数据的丢失。接下来,我们就来详细探讨一下这个问题及其解…...
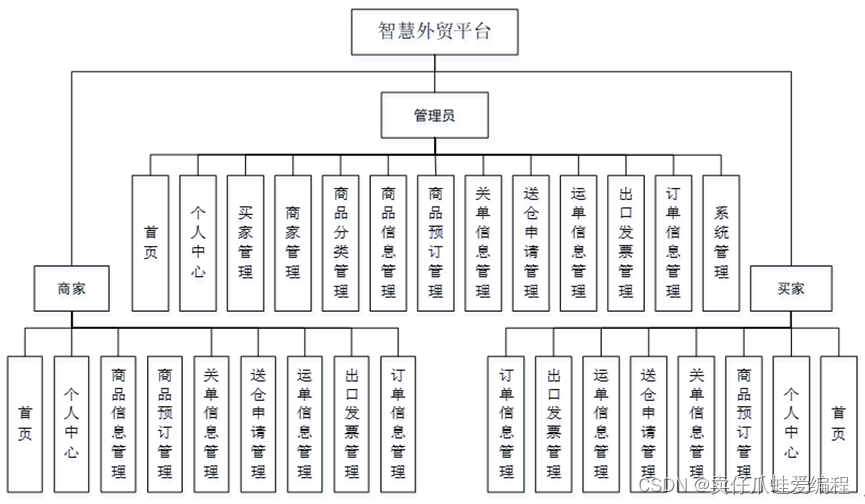
基于springboot+vue的智慧外贸平台
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
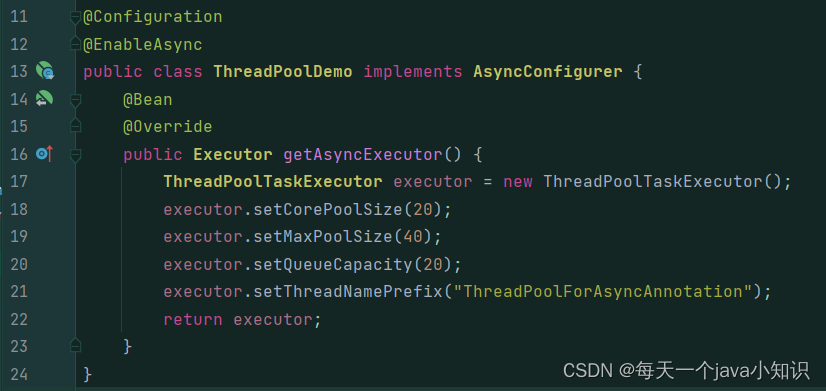
@Async详解,为什么生产环境不推荐直接使用@Async?
一、Async 注解介绍: Async 注解用于声明一个方法是异步的。当在方法上加上这个注解时,Spring 将会在一个新的线程中执行该方法,而不会阻塞原始线程。这对于需要进行一些异步操作的场景非常有用,比如在后台执行一些耗时的任务而不…...

LaTeX 2022软件安装教程(附软件下载地址)
软件简介: 软件【下载地址】获取方式见文末。注:推荐使用,更贴合此安装方法! LaTeX 2022是基于ΤΕΧ的一种排版系统,特别适用于生成科技和数学文档的高质量打印。它可用于各种文档类型,从简单信函到完整…...

纯干货分享 机器学习7大方面,30个硬核数据集
在刚刚开始学习算法的时候,大家有没有过这种感觉,最最重要的那必须是算法本身! 其实在一定程度上忽略了数据的重要性。 而事实上一定是,质量高的数据集可能是最重要的! 数据集在机器学习算法项目中具有非常关键的重…...

算法训练营day46
一、单词拆分 元素无重可复选 base case is.length return true,遍历到了最后, 因为ilen s.length,len初始值为1,那么i1 s.length,那么i s.lenth -1 也就是最后一个字符位置 dp(s,i)函数定义:返回 s[i…] 是否能够…...

推荐五个线上兼职,在家也能轻松日入百元,适合上班族和全职宝妈
在这个瞬息万变的时代,你是否也曾考虑过在繁忙的工作之外,寻找一份兼职副业来补贴家用,同时保持生活的多样性?别急,现在就让我为你揭秘五个可靠的日结线上兼职岗位,助你轻松迈向财务自由之路! 一…...
Python_文件操作_学习
目录 一、关于文件的打开和关闭 1. 文件的打开 2.文件的关闭 二、文件的读取 1. 文件的读_r 2. 使用readline 3.使用readlines 三、文件的写入 1. 文本的新建写入 2.文本的追加写入 四、文件的删除和重命名 1.文件的重命名 2.文件的删除 五、文件的定位读写 1.t…...

Leetcode 3154. Find Number of Ways to Reach the K-th Stair
Leetcode 3154. Find Number of Ways to Reach the K-th Stair 1. 解题思路2. 代码实现 题目链接:3154. Find Number of Ways to Reach the K-th Stair 1. 解题思路 这一题思路上就是一个动态规划,我们只需要确定一下运行的终止条件,然后写…...

Vue3/Vite引入EasyPlayer.js播放H265视频错误的问题
一、引入EasyPlayer.js github链接:GitHub - EasyDarwin/EasyPlayer.js: EasyPlayer.js H5播放器 将demo/html目录下的 EasyPlayer-element.min.js、EasyPlayer-lib.min.js、EasyPlayer.wasm、jquery.min.js 复制到vue3工程的public目录下,注意,vue3 vite的index.html文件…...

CentOS 7安装alertmanager
说明:本文介绍如何在CentOS 7安装alertmanager; Step1:下载安装包 访问Github仓库,下载对应版本的alertmanager安装包 https://github.com/prometheus/alertmanager/releases 如何查看自己系统的信息,可参考下图中的…...
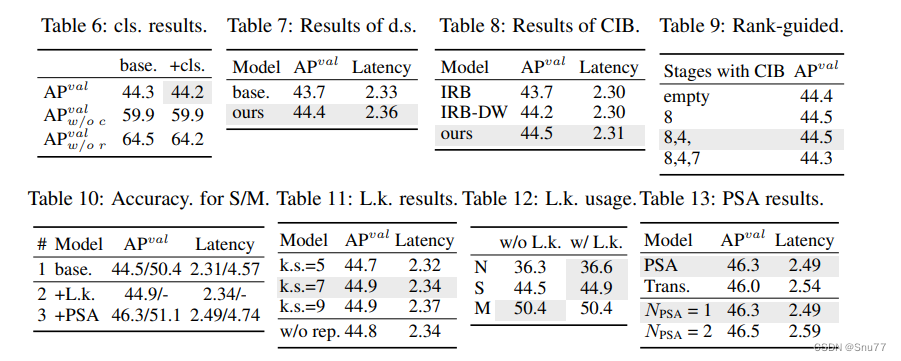
YOLOv10详细解读 | 一文带你深入了解yolov10的创新点(附网络结构图 + 举例说明)
前言 Hello大家好,我是Snu77,继YOLOv9发布时间没有多久,YOLOv10就紧接着发布于2024.5.23号(不得不感叹YOLO系列的发展速度,但要纠正大家的观点就是不是最新的就一定最好)! 本文给大家带来的是…...

【openlayers系统学习】3.5colormap详解(颜色映射)
五、colormap详解(颜色映射) colormap 包是一个很好的实用程序库,用于创建颜色图。该库已作为项目的依赖项添加(1.7美化(设置style))。要导入它,请编辑 main.js 以包含以下行…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
