数据插值之朗格朗日插值(一)
目录
一、引言
二、代码实现
2.1 Lagrange插值求插值多项式:
代码解析:
1.vpa解释
2.ploy(x)解释:
3.conv()解释
4.poly2sym()解释
2.2 Lagrange插值求新样本值和误差估计:
代码解析:
1.errorbar(x, y, R, '.g')
2.plot(X, Y, 'or')
三、Lagrange在Matlab中的使用模板
一、引言
数据插值是指通过有限个原始数据点构造出一个解析表达式,从而可以计算数据点之间的函数值。在Matlab中数据插值的方法主要有拉格朗日插值、牛顿差值、三次样条插值、埃尔米特插值、一维数据插值、二维数据插值等等。笔者旨在写一个使用Matlab进行数值插值的专题,通过介绍插值原理,代码实现,形成模板,方便日后使用时直接代入参数直接调用。
本节介绍拉格朗日插值(Lagrange interpolation)。Lagrange插值是一种用于逼近通过给定数据点的函数的方法。它涉及构造一个度数为 ( n-1 ) 或更低的多项式,该多项式通过 ( n ) 个给定点。该多项式是使用Lagrange基多项式构造的,这是一组多项式,当在给定点之一进行评估时,会得到1,并且当在任何其他给定点进行评估时会得到0。
Lagrange插值多项式可表示为:
Lagrange插值基函数可以表示为:
二、代码实现
2.1 Lagrange插值求插值多项式:
function[C, L, L1, l] = lagranl(X, Y)
% 定义拉格朗日插值多项式和基函数
%
% 输入:
% X - 插值节点的横坐标向量
% Y - 插值节点的纵坐标向量
%
% 输出:
% C - 拉格朗日插值多项式的系数向量
% L - 拉格朗日插值多项式的符号表达式
% L1- 拉格朗日基函数对应的系数矩阵
% l - 拉格朗日基函数对应的符号表达式m = length(X); % 获取插值节点的个数L1 = zeros(m, m); % 初始化存储拉格朗日基函数系数的矩阵
l = sym(zeros(1, m)); % 初始化单行符号值存储基函数表示式for k = 1:m % 遍历每一个插值节点V = 1; % 初始化基函数的系数向量为1for i = 1 : m % 遍历所有节点用于计算if k ~= i %排除掉自身的情况V = conv(V, poly(X(i))) / (X(k) - X(i)); % 更新基函数的系数向量endendL1(k, :) = V; % 存储第k个基函数的系数l(k) = poly2sym(V) * Y(k); % 将基函数乘以对应的Y值,转换为符号表达式并存储
endC = sum(Y .* L1, 1); % 计算拉格朗日插值多项式的系数向量
L = sum(l); % 计算拉格朗日插值多项式的符号表达式下面进行测试:
X = [-2.2, -1.0, 0.01, 1.0, 2.0, 3.3, 2.2];
Y = [17.1, 7.3, 1.1, 2.0, 17.1, 23.1, 19.3];
[C, L, L1, l] = lagranl(X, Y);
L = vpa(L, 3)
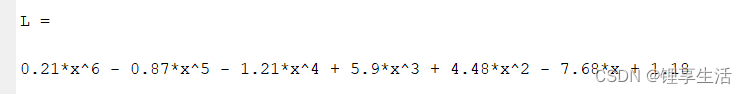
代码解析:
1.vpa解释
vpa 是 MATLAB 中的一个函数,表示 “Variable Precision Arithmetic”(可变精度计算)。在这个特定的调用中,vpa(L, 3) 将 L 的符号表达式以3位小数的精度表示。具体解释:
L: 是从lagranl函数中返回的拉格朗日插值多项式的符号表达式。vpa(L, 3): 会将这个符号表达式的系数和结果值保留到小数点后3位。
假如:
L = sym('0.123456789*x^2 + 0.987654321*x + 3.141592653');使用 vpa 后:
L = vpa(L, 3)
% 将变为
L = sym('0.123*x^2 + 0.988*x + 3.14');2.ploy(x)解释:
在MATLAB中,ploy(x)函数并不是直接用来创建多项式的,容易与用于多项式插值的ployfit()或构造多项式系数的polyval()函数混淆。实际上,ploy(x)函数是用来从根求多项式的系数的。也就是说,如果你有一系列的复数或实数根,poly() 可以帮助你找到一个多项式,其在这些点上的值为零。
基本用法:
p = poly(r)r是一个向量,包含了多项式的根。p是返回的结果,是一个向量,表示对应于根r的多项式的系数,按降幂排列。
举个例子:
r = [1, 2];
p = poly(r);
disp(p); % 输出多项式系数
这段代码会输出 [1 -3 2],对应于多项式,验证了1和2确实是这个多项式的根。
3.conv()解释
conv是MATLAB 中用来执行多项式卷积(Convolution)的函数。在多项式运算中,conv 可以用来计算两个多项式的乘积。
基本用法
C = conv(A, B)其中 A 和 B 是两个多项式的系数向量,返回向量 C 表示这两个多项式的乘积的系数。
示例:
假设我们有两个多项式:
用系数向量表示:
P = [3, 2, 1]; % 对应:
Q = [5, 4]; % 对应:
我们使用conv来计算两者的乘积:
P = [3, 2, 1]; % 3x^2 + 2x + 1
Q = [5, 4]; % 5x + 4C = conv(P, Q)% 输出 C
% C = [15 22 13 4] 对应最终方程式:15x^3 + 22x^2 + 13x + 4
4.poly2sym()解释
poly2sym()是把多项式系数转换为符号多项式。
2.2 Lagrange插值求新样本值和误差估计:
%% 拉格朗日插值及误差估计
% 此函数使用拉格朗日插值公式来计算插值值,并估计误差
% 输入参数:
% X - 已知数据点的x坐标 (向量)
% Y - 已知数据点的y坐标 (向量)
% x - 需要插值的x坐标 (向量)
% M - 最大连续(n+1)阶导数的上界 (标量)
% 输出参数:
% y - 插值后的y值 (向量)
% R - 误差估计 (向量)function [y, R] = lagranzi(X, Y, x, M)n = length(X); % 已知数据点的数量m = length(x); % 需要插值的数据点数量for i = 1:mz = x(i); % 当前需要插值的x坐标s = 0.0; % 插值和初始化为0for k = 1:np = 1.0; % 插值多项式L_k(z)初始化为1q1 = 1.0; % 误差估计中的分子初始化为1c1 = 1.0; % 误差估计中的分母初始化为1for j = 1:nif j ~= k% 计算拉格朗日基函数L_k(z)p = p * (z - X(j)) / (X(k) - X(j));end% 计算误差估计的分子部分q1 = abs(q1 * (z - X(j)));% 计算误差估计的分母部分c1 = c1 * j;end% 加权求和得到插值值s = p * Y(k) + s;endy(i) = s; % 存储插值结果R(i) = M * q1 / c1; % 计算并存储误差估计end
end
下面进行测试:
clc
clear
X = [-2.2, -1.0, 0.01, 1.0, 2.0, 3.3, 2.2];
Y = [17.1, 7.3, 1.1, 2.0, 17.1, 23.1, 19.3];
x = linspace(-3, 4, 50);
M = 1;
[y, R] = lagranzi(X, Y, x, M);
errorbar(x, y, R, '.g')
hold on
plot(X, Y, 'or')
x = 2.8;
[y, R] = lagranzi(X, Y, x, M);
x = -3:0.01:4;
L = 0.21*x.^6 - 0.87*x.^5 - 1.21*x.^4 + 5.9*x.^3 + 4.48*x.^2 - 7.68*x + 1.18;
plot(x, L)
legend('误差', '样本点', '拉格朗日多项式函数曲线')
print(gcf, '-r600', '-djpeg', '图2-1.jpg')

代码解析:
1.errorbar(x, y, R, '.g')
在MATLAB中,errorbar() 函数用于绘制带有误差条的图形,它能够直观地展示数据点的不确定度或误差范围。函数调用格式中的各个参数含义如下:
errorbar(x, y, R, '.g')这里各参数的含义是:
x:数据点,在x轴上的值。y:数据点,与x对应,在y轴上的值。R:这可以是一个向量或一个矩阵,定义了误差条的长度。如果是向量,那么这个向量提供了每个数据点y方向上的误差估计;如果是矩阵(通常是2列),第一列是负方向的误差,第二列是正方向的误差,用于分别表示y值的下限和上限。'.':这是一个标记符号参数,指定了数据点的样式,在这个例子中使用的是点。'g':颜色代码,指定了数据点和误差条的颜色,在这里是绿色。
2.plot(X, Y, 'or')
'o'表示数据点将以圆圈形式标记。如果只用'o',MATLAB 会在每个(X, Y)数据对的位置绘制一个空心的圆圈。'r'表示红色(red)。结合前面的'o',这意味着每个数据点将以红色填充的圆圈来表示。
三、Lagrange插值使用模板
如果目前你拥有X,Y样本点,仅想求出一个新的x所对应的y值,可以直接在下述代码中进行修改“示意用法”中的值,程序放入Matlab中可以直接执行:
clc
clear
% 示例用法
x = [1, 2, 3, 4];
y = [1, 4, 9, 16];
xi = 2.5;
L_value = lagrange_interpolation(x, y, xi);
disp(['在 xi = ' num2str(xi) ' 处的插值值是 ' num2str(L_value)]);function L = lagrange_interpolation(x, y, xi)% 拉格朗日插值函数% x 和 y 是已知的数据点% xi 是希望插值的点% 返回的 L 是在 xi 处的插值结果% 确保 x 和 y 长度一致if length(x) ~= length(y)error('x 和 y 必须具有相同的长度');end% 初始化结果 Ln = length(x);L = 0;% 计算拉格朗日多项式for i = 1:n% 初始化基多项式Li = 1;for j = 1:nif i ~= jLi = Li * (xi - x(j)) / (x(i) - x(j));endend% 累加到结果L = L + Li * y(i);end
end
参考资料:《Matlab编程与汽车仿真应用》 ——崔胜民
相关文章:

数据插值之朗格朗日插值(一)
目录 一、引言 二、代码实现 2.1 Lagrange插值求插值多项式: 代码解析: 1.vpa解释 2.ploy(x)解释: 3.conv()解释 4.poly2sym()解释 2.2 Lagrange插值求新样本值和误差估计: 代码解析&…...

【CCF-CSP】 202309-3 梯度求解
思路: 将表达式整理成只有目标求导变量的无括号加法表达式,其他变量均代入其值,然后利用最简单的求导公式,求出最终值。 样例1 x1 x1 x1 * x2 *转换成 x1*x1*x1x1*x2 若求导x1,则只留下x1,变为 x1*x1*x1…...
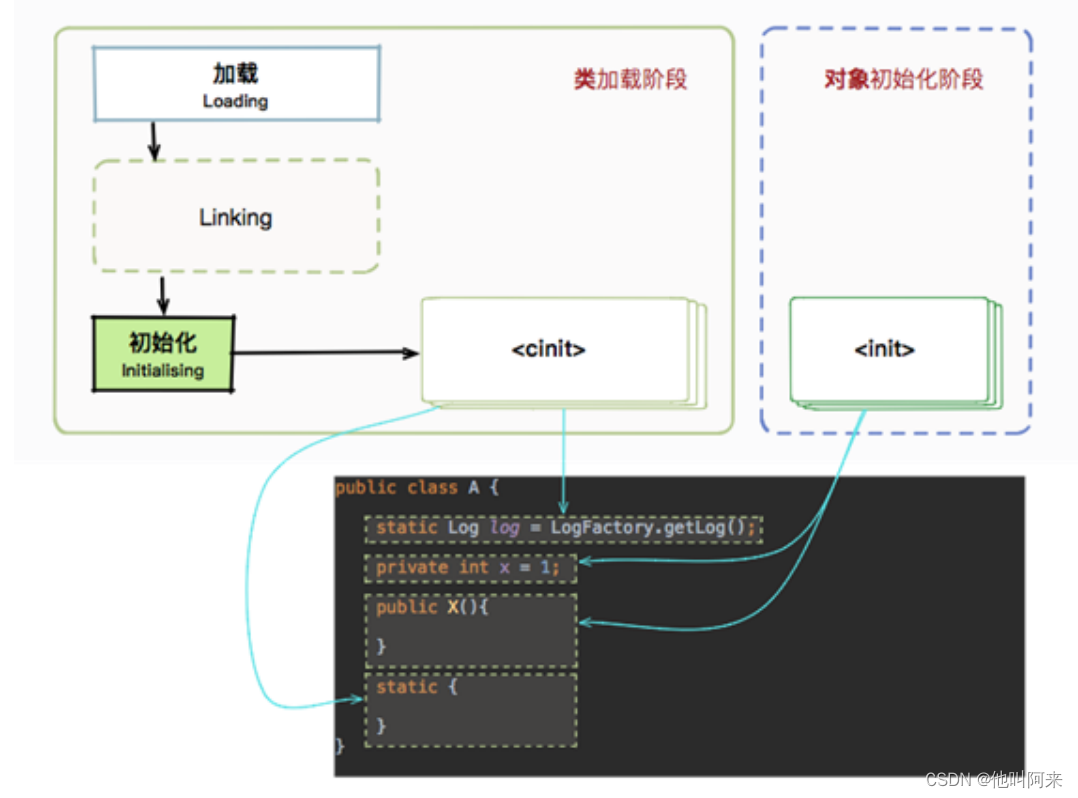
jvm的类加载
文章目录 概要加载类加载器分类双亲委派模型自定义加载器 验证准备解析初始化<cinit>与<init> 概要 jvm运行时的整体结构如下 一个Car类,类跟Car对象的转换过程如下: 加载后的class类信息存放于方法区;ClassLoader只负责clas…...

2024年汉字小达人活动4个多月开赛:18道历年选择题和答案、解析
根据近年的安排,2024年第11届汉字小达人比赛还有4个多月就启动,那么孩子们如何利用这段时间有条不紊地备考呢?我的建议是两手准备:①把小学1-5年级的语文课本上的知识点熟悉,重点是字、词、成语、古诗。②把历年真题刷…...

群晖安装青龙脚本
青龙定时任务管理面板,支持 Python3、JavaScript、Shell、Typescript 这几种环境,通过它可以方便的管理和运行定时任务(在某个时间执行一段代码),并且只需简单的配置,就可以在各个平台收到任务执行的结果通…...

【机器学习系列】使用高斯贝叶斯模型进行数据分类的完整流程
目录 一、导入数据 二、选择特征 三、十折交叉验证 四、划分训练集和测试集 五、训练高斯贝叶斯模型 六、预测测试集 七、查看训练集和测试集上的分数 八、查看混合矩阵 九、输出评估指标 一、导入数据 # 根据商户数据预测其是否续约案例 import pandas #读取数据到 da…...

Python中的单例模式:原理、实现与应用
Python中的单例模式:原理、实现与应用 一、引言 在软件开发中,设计模式是一种用于解决常见问题的最佳实践。单例模式(Singleton Pattern)是这些设计模式中的一种,它确保一个类仅有一个实例,并提供一个全局…...

Linux基础(六):Linux 系统上 C 程序的编译与调试
本篇博客详细分析,Linux平台上C程序的编译过程与调试方法,这也是我们后续程序开发的基础。 目录 一、第一个hello world程序 1.1 创建.c文件 1.2 编译链接 运行可执行程序 二、编译链接过程 2.1 预编译阶段 2.2 编译阶段 2.3 汇编阶段 2.4 链…...

移动硬盘难题:不显示容量与无法访问的解决策略
在使用移动硬盘的过程中,有时会遇到一些棘手的问题,比如移动硬盘不显示容量且无法访问。这种情况让人十分头疼,因为它不仅影响了数据的正常使用,还可能导致重要数据的丢失。接下来,我们就来详细探讨一下这个问题及其解…...
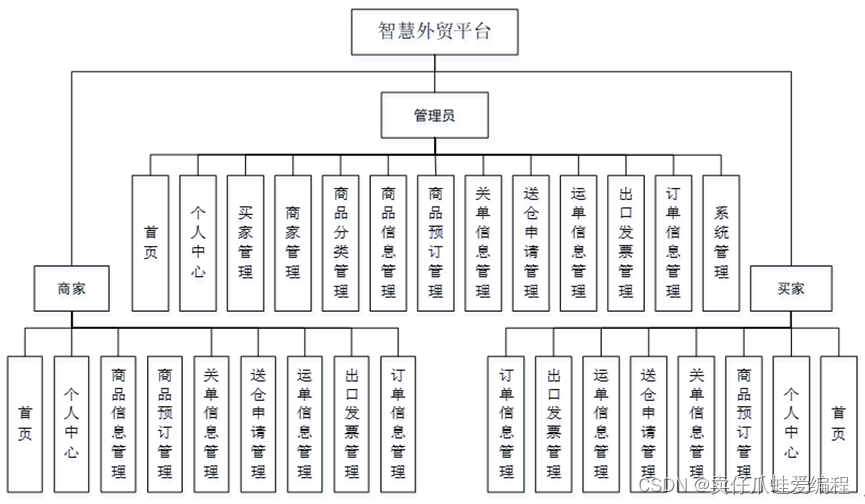
基于springboot+vue的智慧外贸平台
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
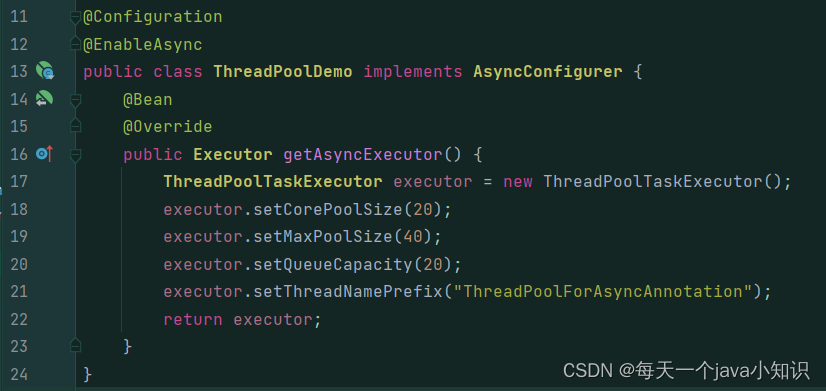
@Async详解,为什么生产环境不推荐直接使用@Async?
一、Async 注解介绍: Async 注解用于声明一个方法是异步的。当在方法上加上这个注解时,Spring 将会在一个新的线程中执行该方法,而不会阻塞原始线程。这对于需要进行一些异步操作的场景非常有用,比如在后台执行一些耗时的任务而不…...

LaTeX 2022软件安装教程(附软件下载地址)
软件简介: 软件【下载地址】获取方式见文末。注:推荐使用,更贴合此安装方法! LaTeX 2022是基于ΤΕΧ的一种排版系统,特别适用于生成科技和数学文档的高质量打印。它可用于各种文档类型,从简单信函到完整…...

纯干货分享 机器学习7大方面,30个硬核数据集
在刚刚开始学习算法的时候,大家有没有过这种感觉,最最重要的那必须是算法本身! 其实在一定程度上忽略了数据的重要性。 而事实上一定是,质量高的数据集可能是最重要的! 数据集在机器学习算法项目中具有非常关键的重…...

算法训练营day46
一、单词拆分 元素无重可复选 base case is.length return true,遍历到了最后, 因为ilen s.length,len初始值为1,那么i1 s.length,那么i s.lenth -1 也就是最后一个字符位置 dp(s,i)函数定义:返回 s[i…] 是否能够…...

推荐五个线上兼职,在家也能轻松日入百元,适合上班族和全职宝妈
在这个瞬息万变的时代,你是否也曾考虑过在繁忙的工作之外,寻找一份兼职副业来补贴家用,同时保持生活的多样性?别急,现在就让我为你揭秘五个可靠的日结线上兼职岗位,助你轻松迈向财务自由之路! 一…...
Python_文件操作_学习
目录 一、关于文件的打开和关闭 1. 文件的打开 2.文件的关闭 二、文件的读取 1. 文件的读_r 2. 使用readline 3.使用readlines 三、文件的写入 1. 文本的新建写入 2.文本的追加写入 四、文件的删除和重命名 1.文件的重命名 2.文件的删除 五、文件的定位读写 1.t…...

Leetcode 3154. Find Number of Ways to Reach the K-th Stair
Leetcode 3154. Find Number of Ways to Reach the K-th Stair 1. 解题思路2. 代码实现 题目链接:3154. Find Number of Ways to Reach the K-th Stair 1. 解题思路 这一题思路上就是一个动态规划,我们只需要确定一下运行的终止条件,然后写…...

Vue3/Vite引入EasyPlayer.js播放H265视频错误的问题
一、引入EasyPlayer.js github链接:GitHub - EasyDarwin/EasyPlayer.js: EasyPlayer.js H5播放器 将demo/html目录下的 EasyPlayer-element.min.js、EasyPlayer-lib.min.js、EasyPlayer.wasm、jquery.min.js 复制到vue3工程的public目录下,注意,vue3 vite的index.html文件…...

CentOS 7安装alertmanager
说明:本文介绍如何在CentOS 7安装alertmanager; Step1:下载安装包 访问Github仓库,下载对应版本的alertmanager安装包 https://github.com/prometheus/alertmanager/releases 如何查看自己系统的信息,可参考下图中的…...
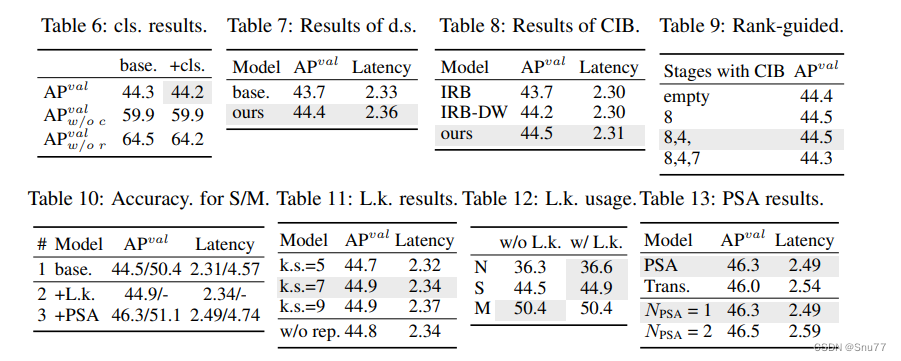
YOLOv10详细解读 | 一文带你深入了解yolov10的创新点(附网络结构图 + 举例说明)
前言 Hello大家好,我是Snu77,继YOLOv9发布时间没有多久,YOLOv10就紧接着发布于2024.5.23号(不得不感叹YOLO系列的发展速度,但要纠正大家的观点就是不是最新的就一定最好)! 本文给大家带来的是…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
