线性回归模型
目录
1.概述
2.线性回归模型的定义
3.线性回归模型的优缺点
4.线性回归模型的应用场景
5.线性回归模型的未来展望
6.小结
1.概述
线性回归是一种广泛应用于统计学和机器学习的技术,用于研究两个或多个变量之间的线性关系。在本文中,我们将深入探讨线性回归模型的定义、优缺点、应用场景以及未来展望。
2.线性回归模型的定义
线性回归模型是一种基于线性假设的统计模型,用于预测一个连续型因变量(也称为响应变量)与一个或多个自变量(也称为解释变量)之间的关系。其基本形式为:
其中,表示因变量,
表示自变量,
是待估参数,
是误差项。该模型假设因变量与自变量之间存在线性关系,并且误差项服从正态分布。
3.线性回归模型的优缺点
1. 优点:
1.线性回归模型可以很好地处理连续型因变量,并且可以预测因变量的取值范围。
2.可以帮助我们理解自变量对因变量的影响程度,以及自变量之间的交互作用。
3.线性回归模型在处理大量数据时非常有效,可以快速地进行参数估计和模型拟合。
4.是一种相对简单和直观的模型,可以通过统计软件轻松实现。
2. 缺点:
1.线性回归模型假设自变量与因变量之间存在线性关系,但在实际问题中,这种假设可能不成立。
2.当自变量之间存在多重共线性时,会导致参数估计不准确,甚至可能导致模型无法拟合数据。
3.线性回归模型对异常值非常敏感,一个异常值可能会极大地影响模型的拟合结果。
4.不能处理高维数据,当自变量数量较多时,模型的计算量和内存需求会迅速增加。
4.线性回归模型的应用场景
1. 预测房价
通过收集房屋的面积、卧室数量、地理位置等信息作为自变量,使用线性回归模型可以预测房屋的价格。
2. 客户流失预测
分析客户的购买历史、消费习惯等数据,建立线性回归模型来预测客户是否会流失。
3. 股票市场预测
利用股票的历史价格、成交量等信息,建立线性回归模型来预测股票的未来走势。
4. 医疗诊断
根据患者的症状、检查结果等数据,建立线性回归模型来辅助医生进行诊断。
5. 物流配送优化
考虑货物的重量、体积、目的地等因素,使用线性回归模型来优化物流配送路线。
6. 信用评估
分析个人的信用记录、收入情况等数据,建立线性回归模型来评估个人的信用风险。
7. 市场调查分析
通过收集消费者的购买意愿、年龄、收入等信息,使用线性回归模型来分析市场需求和趋势。
8. 工程设计
在工程设计中,线性回归模型可以用于优化设计参数,提高产品性能。
我们来举一个用python在jupyter notebook环境下调用相关库实现线性回归模型的例子 :
import numpy as np
from sklearn.linear_model import LinearRegression# 示例数据
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([1, 3, 2, 3, 5])# 创建线性回归模型
model = LinearRegression()# 拟合模型
model.fit(X, y)# 预测新数据
new_X = np.array([[6]])
new_y = model.predict(new_X)print("预测值:", new_y)输出结果:
预测值: [5.2]
在上述代码中,我们首先导入了所需的库 numpy和 scikit-learn.linear_model.LinearRegression。然后,我们定义了示例数据 X和 y。
接下来,我们使用 LinearRegression类创建了一个线性回归模型,并通过 fit方法拟合数据。
然后,我们使用 predict方法预测新数据 new_X的输出值。
最后,我们打印出预测值。
5.线性回归模型的未来展望
1. 深度学习的融合
随着深度学习技术的不断发展,线性回归模型可能会与深度学习结合,以提高模型的性能和泛化能力。
2. 处理高维数据
未来的研究可能会致力于开发更有效的方法来处理高维数据,减少数据的维度或使用特征选择技术。
3. 非线性关系的探索
线性回归模型的局限性在于它只能处理线性关系。未来的研究可能会探索如何将线性回归模型扩展到处理非线性关系。
4. 不确定性估计
更好地估计模型的不确定性,以便在实际应用中做出更可靠的决策。
5. 模型选择和评估的改进
开发更先进的模型选择和评估指标,以帮助用户选择最合适的线性回归模型。
6. 与其他模型的集成
线性回归模型可能会与其他模型(如决策树、随机森林等)进行集成,以提高模型的性能和稳定性。
7. 实时应用的优化
针对实时数据处理的需求,优化线性回归模型的计算效率和内存使用。
8. 可解释性的研究
提高线性回归模型的可解释性,使模型的决策过程更加透明和易于理解。
6.小结
在医疗领域,研究人员可以使用线性回归模型来分析患者的症状和治疗结果之间的关系,以优化治疗方案。在金融领域,模型可以用于预测股票市场的波动,帮助投资者做出更明智的决策。在交通领域,模型可以用于优化交通流量,减少拥堵。这些都是线性回归模型在未来可能的应用场景,通过不断的研究和创新,线性回归模型将继续在各个领域发挥重要作用。
线性回归模型是一种强大而有用的工具,在许多领域都有广泛的应用。虽然存在一些局限性,但通过合理的设计和应用,可以获得较为准确的结果。随着技术的不断进步,线性回归模型的未来发展前景广阔,将为我们的生活和工作带来更多的便利和创新。
相关文章:
线性回归模型
目录 1.概述 2.线性回归模型的定义 3.线性回归模型的优缺点 4.线性回归模型的应用场景 5.线性回归模型的未来展望 6.小结 1.概述 线性回归是一种广泛应用于统计学和机器学习的技术,用于研究两个或多个变量之间的线性关系。在本文中,我们将深入探讨…...

西门子全球业务调整:数十亿欧元交易额,开启新篇章
导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 新书《智能物流系统构成与技术实践》 导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 在风起云涌的全球经济舞台上,西门子&am…...
AI遇上遥感,未来会怎样?
随着航空、航天、近地空间等多个遥感平台的不断发展,近年来遥感技术突飞猛进。由此,遥感数据的空间、时间、光谱分辨率不断提高,数据量也大幅增长,使其越来越具有大数据特征。对于相关研究而言,遥感大数据的出现为其提…...
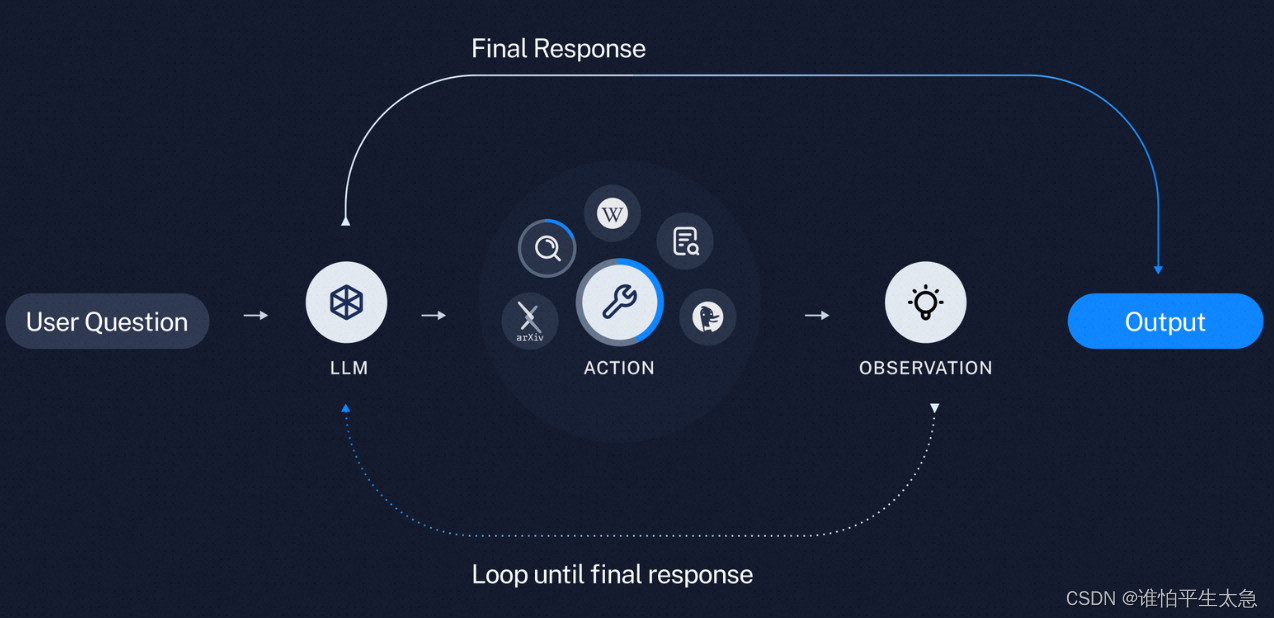
认知架构 cognitive architecture
Assistants API:以开发人员为中心。 有状态的API:允许存储以前的消息、上传文件、访问内置工具(代码解释器)、通过函数调用控制其他工具。 认知架构应用的两个组件:(1)如何提供上下文给应用 &…...

数据插值之朗格朗日插值(一)
目录 一、引言 二、代码实现 2.1 Lagrange插值求插值多项式: 代码解析: 1.vpa解释 2.ploy(x)解释: 3.conv()解释 4.poly2sym()解释 2.2 Lagrange插值求新样本值和误差估计: 代码解析&…...

【CCF-CSP】 202309-3 梯度求解
思路: 将表达式整理成只有目标求导变量的无括号加法表达式,其他变量均代入其值,然后利用最简单的求导公式,求出最终值。 样例1 x1 x1 x1 * x2 *转换成 x1*x1*x1x1*x2 若求导x1,则只留下x1,变为 x1*x1*x1…...
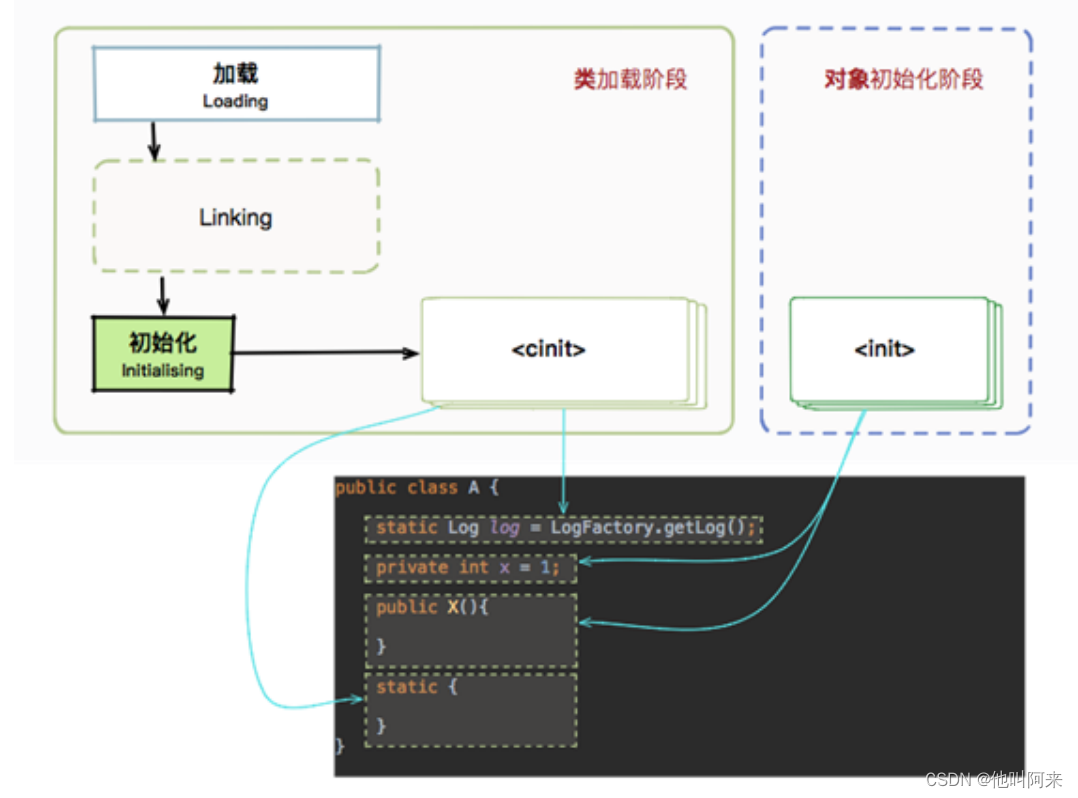
jvm的类加载
文章目录 概要加载类加载器分类双亲委派模型自定义加载器 验证准备解析初始化<cinit>与<init> 概要 jvm运行时的整体结构如下 一个Car类,类跟Car对象的转换过程如下: 加载后的class类信息存放于方法区;ClassLoader只负责clas…...

2024年汉字小达人活动4个多月开赛:18道历年选择题和答案、解析
根据近年的安排,2024年第11届汉字小达人比赛还有4个多月就启动,那么孩子们如何利用这段时间有条不紊地备考呢?我的建议是两手准备:①把小学1-5年级的语文课本上的知识点熟悉,重点是字、词、成语、古诗。②把历年真题刷…...

群晖安装青龙脚本
青龙定时任务管理面板,支持 Python3、JavaScript、Shell、Typescript 这几种环境,通过它可以方便的管理和运行定时任务(在某个时间执行一段代码),并且只需简单的配置,就可以在各个平台收到任务执行的结果通…...

【机器学习系列】使用高斯贝叶斯模型进行数据分类的完整流程
目录 一、导入数据 二、选择特征 三、十折交叉验证 四、划分训练集和测试集 五、训练高斯贝叶斯模型 六、预测测试集 七、查看训练集和测试集上的分数 八、查看混合矩阵 九、输出评估指标 一、导入数据 # 根据商户数据预测其是否续约案例 import pandas #读取数据到 da…...

Python中的单例模式:原理、实现与应用
Python中的单例模式:原理、实现与应用 一、引言 在软件开发中,设计模式是一种用于解决常见问题的最佳实践。单例模式(Singleton Pattern)是这些设计模式中的一种,它确保一个类仅有一个实例,并提供一个全局…...

Linux基础(六):Linux 系统上 C 程序的编译与调试
本篇博客详细分析,Linux平台上C程序的编译过程与调试方法,这也是我们后续程序开发的基础。 目录 一、第一个hello world程序 1.1 创建.c文件 1.2 编译链接 运行可执行程序 二、编译链接过程 2.1 预编译阶段 2.2 编译阶段 2.3 汇编阶段 2.4 链…...

移动硬盘难题:不显示容量与无法访问的解决策略
在使用移动硬盘的过程中,有时会遇到一些棘手的问题,比如移动硬盘不显示容量且无法访问。这种情况让人十分头疼,因为它不仅影响了数据的正常使用,还可能导致重要数据的丢失。接下来,我们就来详细探讨一下这个问题及其解…...
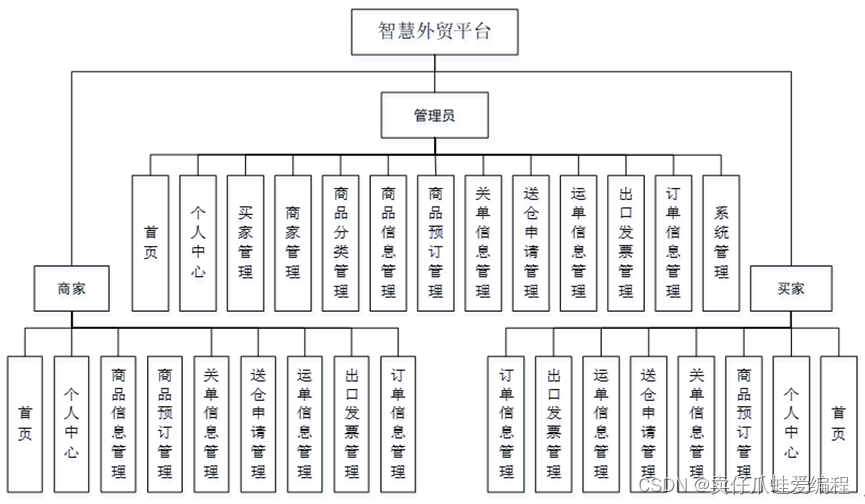
基于springboot+vue的智慧外贸平台
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
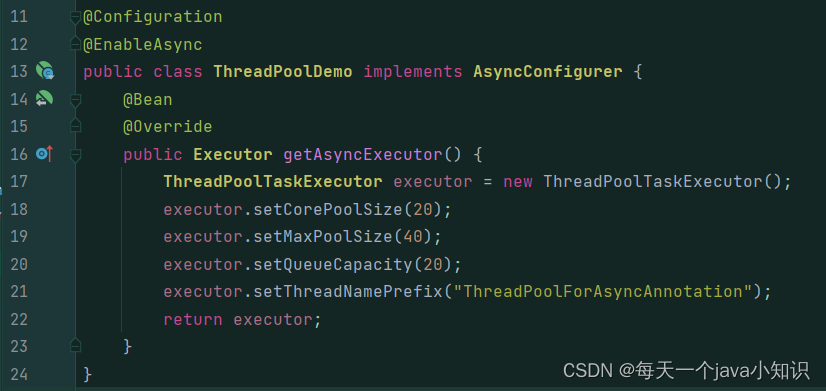
@Async详解,为什么生产环境不推荐直接使用@Async?
一、Async 注解介绍: Async 注解用于声明一个方法是异步的。当在方法上加上这个注解时,Spring 将会在一个新的线程中执行该方法,而不会阻塞原始线程。这对于需要进行一些异步操作的场景非常有用,比如在后台执行一些耗时的任务而不…...

LaTeX 2022软件安装教程(附软件下载地址)
软件简介: 软件【下载地址】获取方式见文末。注:推荐使用,更贴合此安装方法! LaTeX 2022是基于ΤΕΧ的一种排版系统,特别适用于生成科技和数学文档的高质量打印。它可用于各种文档类型,从简单信函到完整…...

纯干货分享 机器学习7大方面,30个硬核数据集
在刚刚开始学习算法的时候,大家有没有过这种感觉,最最重要的那必须是算法本身! 其实在一定程度上忽略了数据的重要性。 而事实上一定是,质量高的数据集可能是最重要的! 数据集在机器学习算法项目中具有非常关键的重…...

算法训练营day46
一、单词拆分 元素无重可复选 base case is.length return true,遍历到了最后, 因为ilen s.length,len初始值为1,那么i1 s.length,那么i s.lenth -1 也就是最后一个字符位置 dp(s,i)函数定义:返回 s[i…] 是否能够…...

推荐五个线上兼职,在家也能轻松日入百元,适合上班族和全职宝妈
在这个瞬息万变的时代,你是否也曾考虑过在繁忙的工作之外,寻找一份兼职副业来补贴家用,同时保持生活的多样性?别急,现在就让我为你揭秘五个可靠的日结线上兼职岗位,助你轻松迈向财务自由之路! 一…...
Python_文件操作_学习
目录 一、关于文件的打开和关闭 1. 文件的打开 2.文件的关闭 二、文件的读取 1. 文件的读_r 2. 使用readline 3.使用readlines 三、文件的写入 1. 文本的新建写入 2.文本的追加写入 四、文件的删除和重命名 1.文件的重命名 2.文件的删除 五、文件的定位读写 1.t…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
