C++学习笔记(19)——模板

目录
模板参数与非类型模板参数
模板参数
类型模板参数——传递类型
非类型模板参数——传递数量
C++11希望array替代静态数组,但实际上vector包揽了一切
模板总结
优点:
缺点:
模板特化:针对某些类型进行特殊化处理
特化
-
模板参数与非类型模板参数
-
模板参数
-
类型模板参数——传递类型
- 传递一些参数(int,double等变量类型)到类的模板,这些参数的类型信息被选择性摘取用于构建一个类,这些参数不占用空间
-
非类型模板参数——传递数量
- 当我们构建模板时想要设置一些静态空间,这时候我们可以传递非类型模板参数;
- 传递一些参数(100等整形变量类型,它被专门用来定义静态数据类型,开静态的空间.
- C++20允许各种变量类型了C++.98只允许整形)到类的模板,这些参数常用明确于成员变量开空间的规格,这些参数参与的开空间占用空间
- 这里的“非类型”是指这些“模板参数”他们不参与类型性质的构建,他们只是提供一个数量规格
- “非类型模板参数”得是常量,否则编译不通过
-
-
知识点
- array数组,本质是一个函数的调用;
- C语言的数组本质是指针的解引用,数组越界是随机抽查,可能检查不出来;
- 设计之初C++11希望array替代静态数组,但实际上vector包揽了一切;
-
-
模板总结
-
优点
- 1.复用代码,节约资源,加速迭代开发,C++标准模板库(STL)因此产生
- 2.增强代码灵活性
-
缺点
- 1.模板会导致代码膨胀问题,也会导致编译时间变长;
- 2.出现模板编译错误时,错误信息非常混乱,不易定位错误;(出错的逻辑会因为逻辑的嵌套而难以发觉)
- 经验:出错了看第一个错误,一般大量错误都是由第一个错误,或者逻辑前面没有报错的代码错误了。
-
-
模板特化:针对某些类型进行特殊化处理
- 在有通用模板的前提下,针对特殊的模板参数组合我们单独去为其建立一个类模板;
- 针对特定的模板参数在通用模板运行时功能失效的情况,我们可以通过模板特化,构建一个特定的模板去处理他;
-
特化
- 全特化:特化全部参数
- 偏特化(半特化):特化部分参数
- 特化也可以使用模板template<class T>
相关文章:

C++学习笔记(19)——模板
目录 模板参数与非类型模板参数 模板参数 类型模板参数——传递类型 非类型模板参数——传递数量 C11希望array替代静态数组,但实际上vector包揽了一切 模板总结 优点: 缺点: 模板特化:针对某些类型进行特殊化处理 特化…...
java8新特性——函数式编程详解
目录 一 概述1.1 背景1.2 函数式编程的意义1.3 函数式编程的发展 Lambda表达式1.1 介绍1.2 使用Lambda的好处1.3 Lambda方法1.3.1 Lambda表达式结构1.3.2 Lambda表达式的特征 1.4 Lambda的使用1.4.1 定义函数式接口1.4.2 Lambda表达式实现函数式接口1.4.3 简化Lambda表达式1.4.…...

mybatis-plus小课堂: apply 拼接 in SQL,来查询从表某个范围内的数据
文章目录 引言I mybatis-Plus 之 apply 拼接 in SQL1.1 apply源码实现1.2 apply 拼接 in SQL : 非字符串数组1.3 apply 拼接 in SQL : 字符串数组II 如果in的数量太多,采用子查询。III 常见问题: Cause: comColumn xxx in where clause is ambiguoussee also引言 I mybati…...

民宿推荐系统-手把手调试搭建
民宿推荐系统-手把手调试搭建 民宿推荐系统-手把手调试搭建...
线性回归模型
目录 1.概述 2.线性回归模型的定义 3.线性回归模型的优缺点 4.线性回归模型的应用场景 5.线性回归模型的未来展望 6.小结 1.概述 线性回归是一种广泛应用于统计学和机器学习的技术,用于研究两个或多个变量之间的线性关系。在本文中,我们将深入探讨…...

西门子全球业务调整:数十亿欧元交易额,开启新篇章
导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 新书《智能物流系统构成与技术实践》 导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 在风起云涌的全球经济舞台上,西门子&am…...
AI遇上遥感,未来会怎样?
随着航空、航天、近地空间等多个遥感平台的不断发展,近年来遥感技术突飞猛进。由此,遥感数据的空间、时间、光谱分辨率不断提高,数据量也大幅增长,使其越来越具有大数据特征。对于相关研究而言,遥感大数据的出现为其提…...
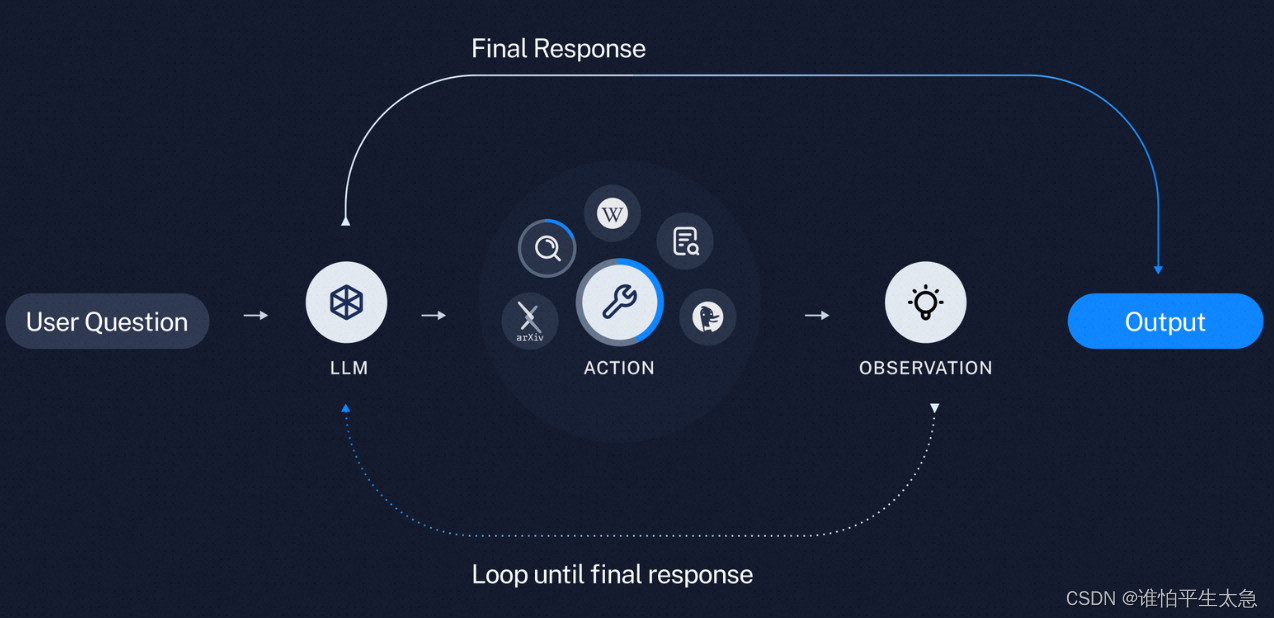
认知架构 cognitive architecture
Assistants API:以开发人员为中心。 有状态的API:允许存储以前的消息、上传文件、访问内置工具(代码解释器)、通过函数调用控制其他工具。 认知架构应用的两个组件:(1)如何提供上下文给应用 &…...

数据插值之朗格朗日插值(一)
目录 一、引言 二、代码实现 2.1 Lagrange插值求插值多项式: 代码解析: 1.vpa解释 2.ploy(x)解释: 3.conv()解释 4.poly2sym()解释 2.2 Lagrange插值求新样本值和误差估计: 代码解析&…...

【CCF-CSP】 202309-3 梯度求解
思路: 将表达式整理成只有目标求导变量的无括号加法表达式,其他变量均代入其值,然后利用最简单的求导公式,求出最终值。 样例1 x1 x1 x1 * x2 *转换成 x1*x1*x1x1*x2 若求导x1,则只留下x1,变为 x1*x1*x1…...
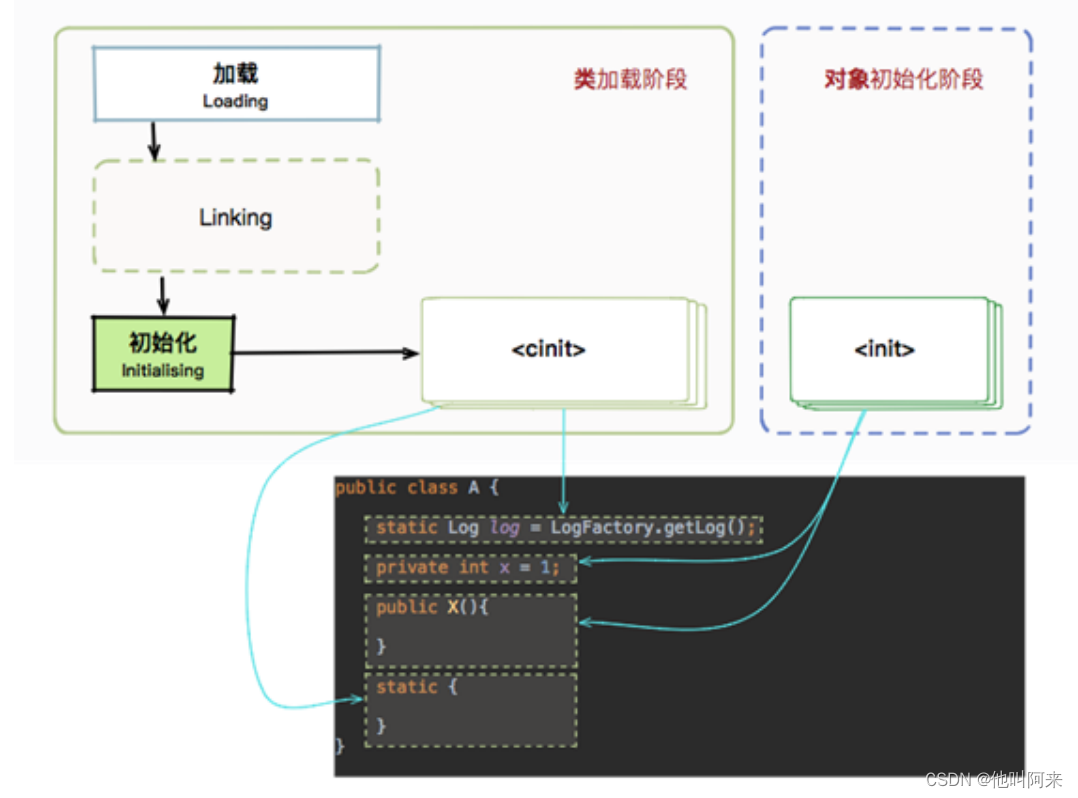
jvm的类加载
文章目录 概要加载类加载器分类双亲委派模型自定义加载器 验证准备解析初始化<cinit>与<init> 概要 jvm运行时的整体结构如下 一个Car类,类跟Car对象的转换过程如下: 加载后的class类信息存放于方法区;ClassLoader只负责clas…...

2024年汉字小达人活动4个多月开赛:18道历年选择题和答案、解析
根据近年的安排,2024年第11届汉字小达人比赛还有4个多月就启动,那么孩子们如何利用这段时间有条不紊地备考呢?我的建议是两手准备:①把小学1-5年级的语文课本上的知识点熟悉,重点是字、词、成语、古诗。②把历年真题刷…...

群晖安装青龙脚本
青龙定时任务管理面板,支持 Python3、JavaScript、Shell、Typescript 这几种环境,通过它可以方便的管理和运行定时任务(在某个时间执行一段代码),并且只需简单的配置,就可以在各个平台收到任务执行的结果通…...

【机器学习系列】使用高斯贝叶斯模型进行数据分类的完整流程
目录 一、导入数据 二、选择特征 三、十折交叉验证 四、划分训练集和测试集 五、训练高斯贝叶斯模型 六、预测测试集 七、查看训练集和测试集上的分数 八、查看混合矩阵 九、输出评估指标 一、导入数据 # 根据商户数据预测其是否续约案例 import pandas #读取数据到 da…...

Python中的单例模式:原理、实现与应用
Python中的单例模式:原理、实现与应用 一、引言 在软件开发中,设计模式是一种用于解决常见问题的最佳实践。单例模式(Singleton Pattern)是这些设计模式中的一种,它确保一个类仅有一个实例,并提供一个全局…...

Linux基础(六):Linux 系统上 C 程序的编译与调试
本篇博客详细分析,Linux平台上C程序的编译过程与调试方法,这也是我们后续程序开发的基础。 目录 一、第一个hello world程序 1.1 创建.c文件 1.2 编译链接 运行可执行程序 二、编译链接过程 2.1 预编译阶段 2.2 编译阶段 2.3 汇编阶段 2.4 链…...

移动硬盘难题:不显示容量与无法访问的解决策略
在使用移动硬盘的过程中,有时会遇到一些棘手的问题,比如移动硬盘不显示容量且无法访问。这种情况让人十分头疼,因为它不仅影响了数据的正常使用,还可能导致重要数据的丢失。接下来,我们就来详细探讨一下这个问题及其解…...
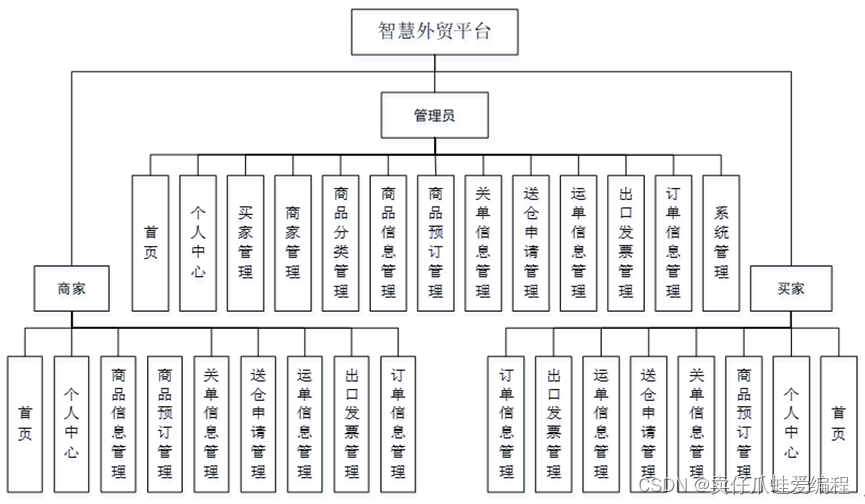
基于springboot+vue的智慧外贸平台
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
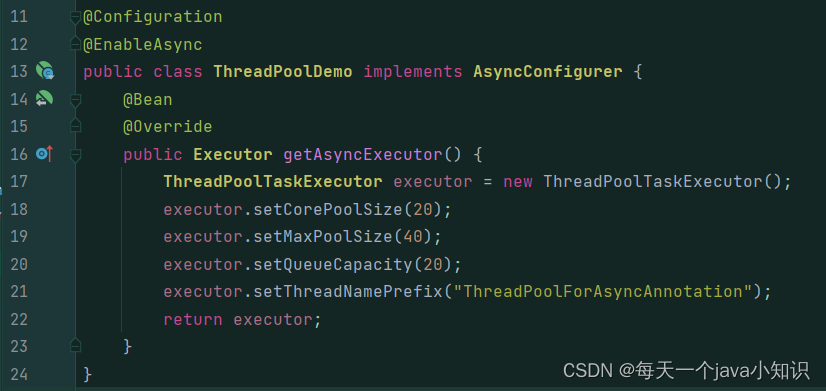
@Async详解,为什么生产环境不推荐直接使用@Async?
一、Async 注解介绍: Async 注解用于声明一个方法是异步的。当在方法上加上这个注解时,Spring 将会在一个新的线程中执行该方法,而不会阻塞原始线程。这对于需要进行一些异步操作的场景非常有用,比如在后台执行一些耗时的任务而不…...

LaTeX 2022软件安装教程(附软件下载地址)
软件简介: 软件【下载地址】获取方式见文末。注:推荐使用,更贴合此安装方法! LaTeX 2022是基于ΤΕΧ的一种排版系统,特别适用于生成科技和数学文档的高质量打印。它可用于各种文档类型,从简单信函到完整…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
