常用激活函数学习
常用激活函数及其应用
-
ReLU (Rectified Linear Unit)
- 公式: f ( x ) = max ( 0 , x ) f(x) = \max(0, x) f(x)=max(0,x)
- 理解: 当输入值为正时,输出等于输入值;否则输出为0。ReLU函数简单且计算效率高,能有效缓解梯度消失问题,促进深层网络的学习。
- 场景与大模型应用: ReLU是深度学习中最常用的激活函数,尤其是在卷积神经网络(CNN)和递归神经网络(RNN)的隐藏层中。著名的模型如VGGNet、ResNet系列广泛使用ReLU及其变体,如ReLU6和Leaky ReLU。
-
Sigmoid
- 公式: f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
- 理解: 将输入映射到(0, 1)之间,常用于需要概率输出的场景,如二元分类问题。但因其饱和特性,导致梯度消失问题。
- 场景与大模型应用: 在早期的神经网络和一些特定任务中使用,如在LSTM的门控机制中控制信息流。现代网络较少在隐藏层使用,因梯度消失问题。
-
Tanh (Hyperbolic Tangent)
- 公式: f ( x ) = e x − e − x e x + e − x f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} f(x)=ex+e−xex−e−x
- 理解: 输出范围在(-1, 1),比Sigmoid具有更好的梯度特性,适用于需要中心化的输出分布。
- 场景与大模型应用: 在循环神经网络如LSTM和GRU的隐藏状态中常用,有助于保持状态的数值稳定性。
-
Softmax
- 公式: f i ( x ) = e x i ∑ j = 1 n e x j f_i(x) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}} fi(x)=∑j=1nexjexi,其中 x x x是向量, f i f_i fi是第 i i i个元素的softmax输出。
- 理解: 将输入向量转换为概率分布,保证所有输出之和为1,非常适合多分类问题。
- 场景与大模型应用: 几乎所有涉及多类别分类的模型输出层都会使用Softmax,如图像分类的ResNet、Inception,以及文本分类的BERT模型。
-
Leaky ReLU
- 公式: f ( x ) = max ( a x , x ) f(x) = \max(ax, x) f(x)=max(ax,x),其中 a a a是一个小于1的正值,通常是0.01。
- 理解: Leaky ReLU是对ReLU的一个改进,允许负数输入有非零斜率的输出,有助于解决“死亡ReLU”问题。
- 场景与大模型应用: 适用于需要缓解ReLU死区问题的模型,虽然不像ReLU那样普遍,但在某些特定模型或层中仍然可见。
这些激活函数的选择取决于具体任务的需求,如是否需要输出概率、是否关注梯度消失或爆炸问题,以及模型的深度等因素。不同的激活函数在不同的大模型中有其独特的应用场景,优化模型性能和学习能力。
相关文章:

常用激活函数学习
常用激活函数及其应用 ReLU (Rectified Linear Unit) 公式: f ( x ) max ( 0 , x ) f(x) \max(0, x) f(x)max(0,x)理解: 当输入值为正时,输出等于输入值;否则输出为0。ReLU函数简单且计算效率高,能有效缓解梯度消失问题,促进…...

html中被忽略的简单标签
1: alt的作用是在图片不能显示时的提示信息 <img src"https://img.xunfei.cn/mall/dev/ifly-mall-vip- service/business/vip/common/202404071019208761.jp" alt"提示信息" width"100px" height"100px" /> 2&#…...
Vue.Draggable:强大的Vue拖放组件技术探索
一、引言 随着前端技术的不断发展,拖放(Drag-and-Drop)功能已经成为许多Web应用不可或缺的一部分。Vue.js作为现代前端框架的佼佼者,为开发者提供了丰富的生态系统和强大的工具链。Vue.Draggable作为基于Sortable.js的Vue拖放组件…...

linux mail命令及其历史
一、【问题描述】 最近隔壁组有人把crontab删了,crontab这个命令有点反人类,它的参数特别容易误操作: crontab - 是删除计划表 crontab -e 是编辑,总之就是特别容易输入错误。 好在可以通过mail命令找回,但是mai…...
和以数据为中心(Data-Centric)的区别)
数据驱动(Data-Driven)和以数据为中心(Data-Centric)的区别
一、什么是数据驱动? 数据驱动(Data-Driven)是在管理科学领域经常提到的名词。数据驱动决策(Data-Driven Decision Making,简称DDD)是一种方法论,即在决策过程中主要依赖于数据分析和解释&…...

aosp14的分屏接口ISplitScreen接口获取方式更新-学员疑问答疑
背景: 有学员朋友在学习马哥的分屏pip自由窗口专题时候,做相关分屏做小桌面项目时候,因为原来课程版本是基于android 13进行的讲解的,但是现在公司已经开始逐渐进行相关的android 14的适配了,但是android 14这块相比a…...
定积分求解过程是否变限问题 以及当换元时注意事项
目录 定积分求解过程是否变限问题 文字理解: 实例理解: 易错点和易混点: 1:定积分中的换元指什么? 2: 不定积分中第一类换元法和第二类换元法的本质和区别 3: df(x) ----> df(x)这…...
)
保研机试算法训练个人记录笔记(七)
输入格式: 在第1 行给出不超过10^5 的正整数N, 即参赛}人数。随后N 行,每行给出一位参赛者的 信息和成绩,包括其所代表的学校的编号(从1 开始连续编号)及其比赛成绩(百分制)…...
-查询优化(23)-避免全表扫描)
【MySQL精通之路】SQL优化(1)-查询优化(23)-避免全表扫描
当MySQL使用全表扫描来解析查询时,EXPLAIN的输出在type列中显示ALL。 这种情况通常发生在以下情况下: 该表非常小,因此执行全表扫描比查找关键字更快。这对于少于10行且行长较短的表来说很常见。 对于索引列,ON或WHERE子句中没有…...
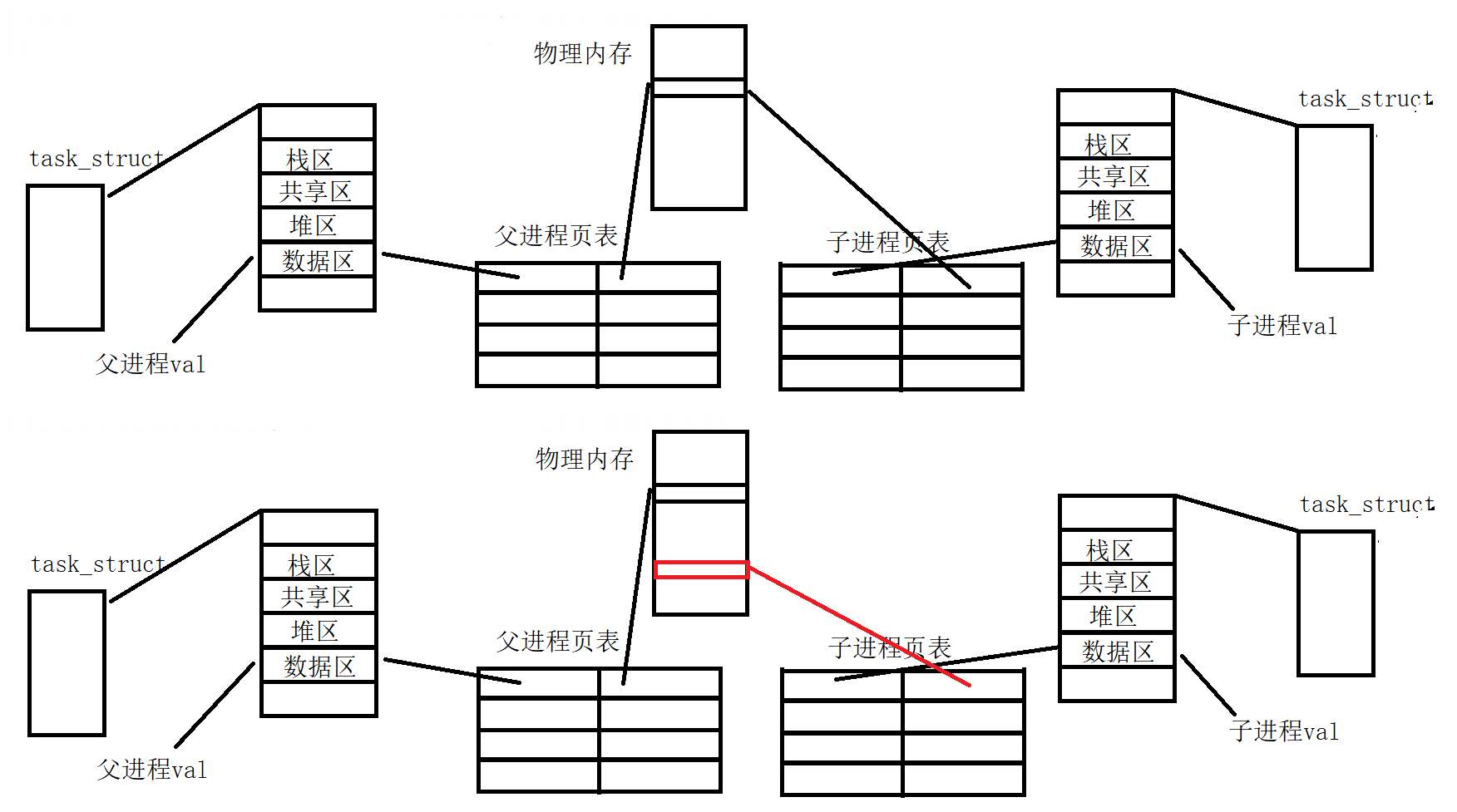
【Linux】写时拷贝技术COW (copy-on-write)
文章目录 Linux写时拷贝技术(copy-on-write)进程的概念进程的定义进程和程序的区别PCB的内部构成 程序是如何被加载变成进程的?写时复制(Copy-On-Write, COW)写时复制机制的原理写时拷贝的场景 fork与COWvfork与fork Linux写时拷贝技术(copy-…...

用python使用主成分分析数据
import pandas as pd #导入处理二维表格的库 import numpy as np #导入数值计算的库 from sklearn.preprocessing import StandardScaler #导入数据标准化模块 import matplotlib.pyplot as plt #导入画图的包 from sklearn.decomposition import PCA #导入主成…...

用WPS将多张图片生成一个pdf文档,注意参数设置
目录 1 新建一个docx格式的文档 2 向文档中插入图片 3 设置页边距 4 设置图片大小 5 导出为pdf格式 需要把十几张图片合并为一个pdf文件,本以为很简单,迅速从网上找到两个号称免费的在线工具,结果浪费了好几分钟时间,发现需要…...
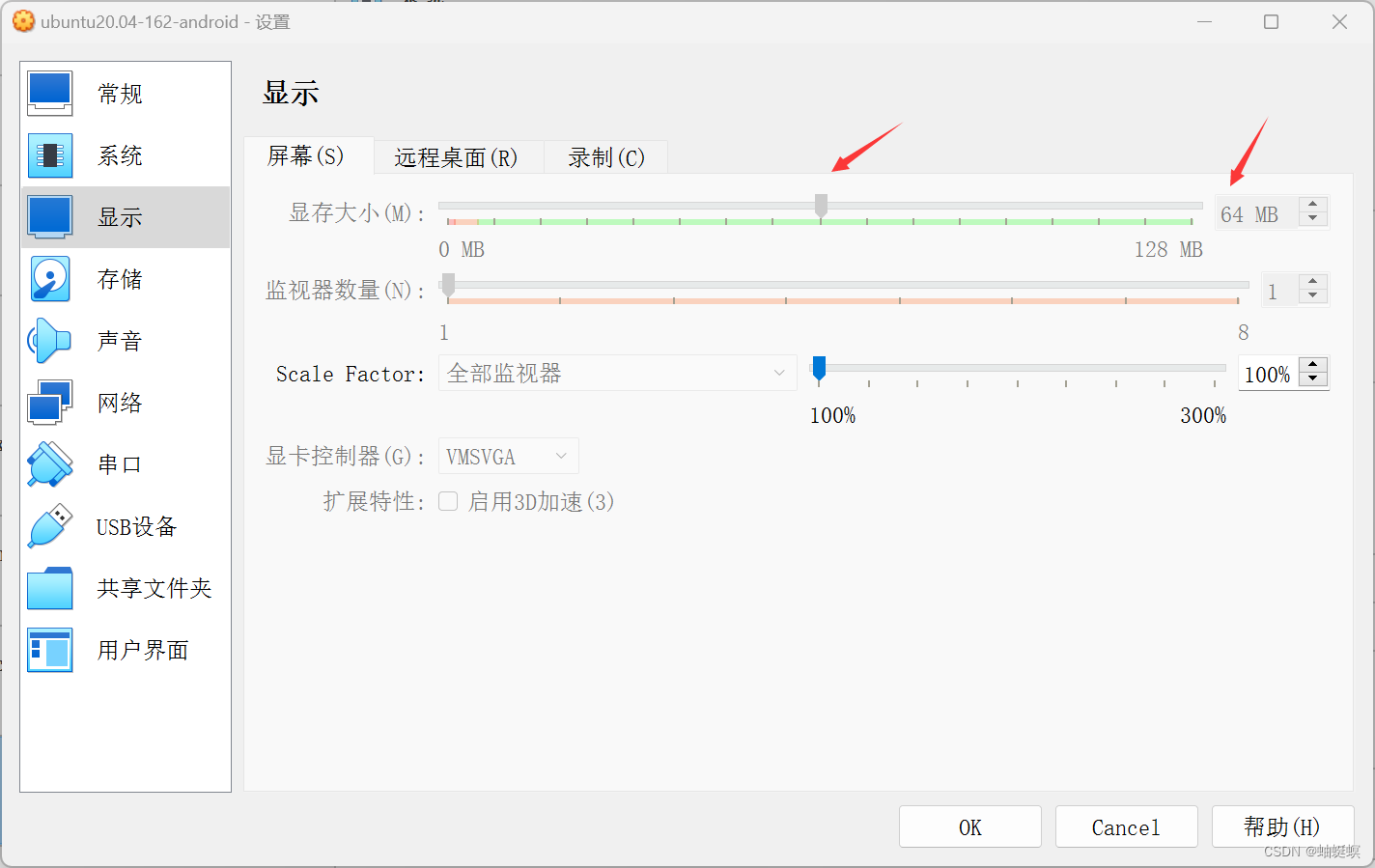
virtual box ubuntu20 全屏展示
virtual box 虚拟机 ubuntu20 系统 全屏展示 ubuntu20.04 视图-自动调整窗口大小 视图-自动调整显示尺寸 系统黑屏解决 ##设备-安装增强功能 ##进入终端 ##终端打不开,解决方案-传送门ubuntu Open in Terminal打不开终端解决方案-CSDN博客 ##点击cd盘按钮进入文…...
的使用)
react中的数据驱动视图,useState()的使用
前端开发如今有一个很重要的思想就是数据驱动视图,数据发生变化使ui发生变化,比如一个变量count,为0显示三个按钮,为1显示一个按钮,为2显示两个按钮。这就是一个简单的数据驱动视图。 import { useState } from reactf…...

金融数据库,实时行情,股票财务数据在线查询
jvQuant在线SQL 文档(current)接入 测试 查询 #股票代码股票简称最新价(元)2024-05-21股东总户数(户)截至2024-05-21上市板块是否ST股票区间涨跌幅(%)2024-05-15-2024-05-21市盈率(TTM)(倍)2024-05-21营业收入(元)截至2024-03-31总市值(元)2024-05-21量比2024-05-21利润率(%…...
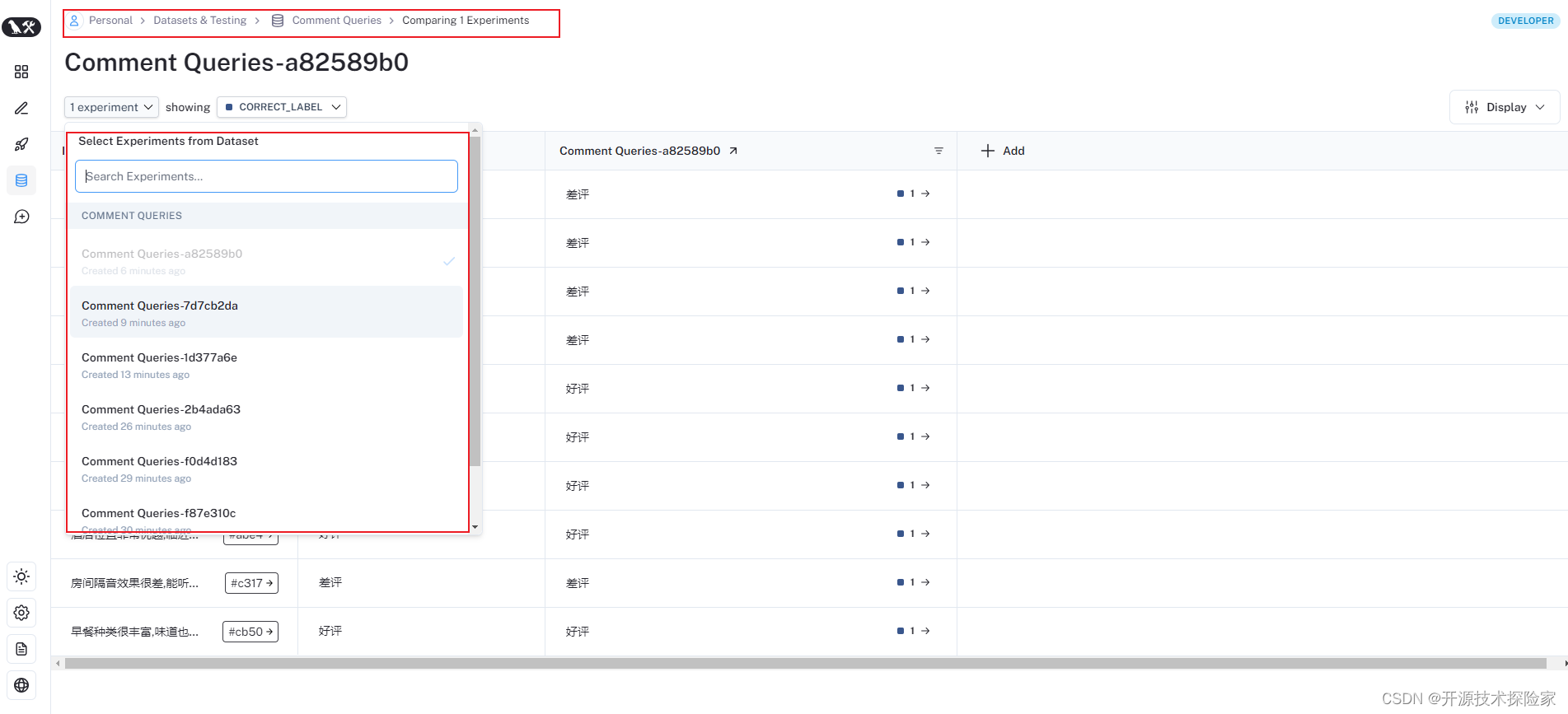
开源模型应用落地-LangSmith试炼-入门初体验-数据集评估(三)
一、前言 LangSmith是一个用于构建生产级 LLM 应用程序的平台,它提供了调试、测试、评估和监控基于任何 LLM 框架构建的链和智能代理的功能,并能与LangChain无缝集成。通过使用LangSmith帮助开发者深入了解模型在不同场景下的表现,让开发者能…...

设计模式 15 Decorator Pattern 装饰器模式
设计模式 15 Decorator Pattern 装饰器模式 1.定义 Decorator Pattern 装饰器模式是一种结构型设计模式,它允许在运行时给对象添加新的行为或职责,而无需修改对象的源代码。这种模式通过创建一个包装对象,也称为装饰器,来包裹原…...

cuda11.8安装torch2.0.1
pip install torch2.0.1 torchvision0.15.2 torchaudio2.0.2 --index-url https://download.pytorch.org/whl/cu118...

新手困 ViewModel与Activting的databinding2个对象 区别
在Android开发中,ViewModel与Activity的Binding并不是同一个概念,它们分别指的是不同的功能和用途。 ViewModel: ViewModel是一个为UI界面提供数据的类,它负责管理Activity或Fragment的数据。ViewModel类持有数据的引用,即使配置…...

Cocos Creator 声音播放与管理详解
Cocos Creator 是一款非常流行的游戏开发引擎,它提供了丰富的功能和工具,让开发者可以轻松构建出高质量的游戏。在游戏开发中,声音是一个非常重要的元素,可以为游戏增添氛围和趣味性。在本文中,我们将详细介绍Cocos Cr…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
