四大进制--详解--以及进制转换规则
- 进制介绍
对于整数, 有四种表达方式:
- 二进制BIN: 0,1 , 满2进1.以0b或0B开头
所谓2进制就是使用0和1来表示一个数, 满2进1如果在开发中看到有这种写法: int n1 = 0b1010; 这种写法没有错, 这是二进制的一种表示方式
- 十进制DEC: 0-9, 满10进1
十进制就是0-9来表示一个数, 满10进1
- 八进制OCT: 0-7, 满8进1. 以数字0开头表示.
比如 int n3 = 01010; 代表它是用八进制来表示一个数的
- 十六进制HEX: 0-9及A(10)-F(15), 满16进1. 以0x或0X开头表示. 此处的A-F不区分大小写.
十六进制它是用0-9以及A(10)-F(15)来表示一个数的, 以0x或0X开头表示 比如A表示10, B表示11, C表示12, D表示13, E表示14, F表示15, 到了15过后16就没有了因为它满16进1
- 举例说明
int n1 = 0b1010; //二进制的表示方式int n2 = 1010; //十进制int n3 = 01010; //八进制int n4 = 0x10101; //0X10101 十六进制System.out.println("n1 =" + n1);System.out.println("n2 =" + n2);System.out.println("n3 =" + n3);System.out.println("n4 =" + n4);- 进制的图示
| 十进制 | 十六进制 | 八进制 | 二进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
进制转换(基本功)
- 进制转换介绍
第一组
- 二进制转十进制
规则:
从最低位(右边)开始, 将每个位上的数提取出来, 乘以2的(位数-1)次方, 然后求和.
案例:请将 0b1011 转成十进制的数
0b1011 = 1 * 2的(1-1)次方 + 1 * 2 的(2 - 1)次方 + 0 * 2的(3-1)次方 + 1 * 2的(4-1)次方 = 1 + 2 + 0 + 8 = 11
- 八进制转十进制
规则:
从最低位(右边)开始, 将每个位上的数提出来, 乘以8的(位数-1)次方,然后求和.
案例: 请将 0234 转成 十进制的数
0234 = 4 * 8 ^ 0 + 3 * 8 ^ 1 + 2 * 8^2= 4 + 24 + 128 = 156
- 十六进制转十进制
规则:
从最低位(右边)开始, 将每个位上的数提取出来, 乘以16的(位数-1)次方, 然后求和
案例: 请将 0x23A 转成 十进制的数
0x23A = 10 * 16^0 + 3 * 16 ^ 1 + 2 * 16 ^ 2 =10 +48 + 64 + 512 = 570
第二组
- 十进制转二进制
规则:
将该数不断除以2, 直到商为0为止, 然后将每步得到的余数倒过来, 就是对应的二进制
案例: 请将 34 转成 二进制的数
34 = 34 ➗ 2 = 17 余数为 0 再将 17 ➗ 2 = 8 余数为1 再将 8 ➗2 = 4 余数为0 再将 2 除以 2 商1 余数为 0 然后反过来 为 = 0B100010 , 她一共有6位但是我们一个字节是我们存储的基本单位一个字节有8位所以在这里0B后还要再加两个0, 最终得到的二进制为0B00100010
- 十进制转八进制
规则:
将该数不断除以8, 直到商为0为止, 然后将每步得到的余数倒过来, 就是对应的八进制
案例: 请将 131 转成 八进制的数
131 ➗8 商为 16 余数为 3 , 再 ➗8 , 16 ➗ 8 商为 2 余数为0 最后得到的8进制的数为 0203
- 十进制转十六进制
规则:
将该数不断除以16, 直到商为0为止, 然后将每步得到的余数倒过来, 就是对应的十六进制
案例: 请将 237转成 十六进制的数
237➗16 商为 14 在16进制里 14对应的字母是E 余数为 13 , 在 16 进制里 13对应的字母是 D ,所以说结果是 0xED
第三组
- 二进制转八进制
规则:
从低位开始, 将二进制数每三位一组, 转成对应的八进制数即可.
案例: 请将 0b11010101 转成 八进制的数
每三个一组 101(5) => 为什么是5? 因为第一个1代表1 , 第二个1代表2, 第三个1代表四所以4加一等于五
010(2) => 0就是0 1为2 再一个0还是0所以为2
11(3)
结果为 0325
- 二进制转十六进制
规则:
从低位开始, 将二进制数每四位一组, 转成对应的十六进制数即可.
案例: 请将 0b11010101 转成 十六进制的数
每四个一组 0101(5) => 0x
1101(13) => 13为D 所以 1101(D)
11(3)
结果为 0325
第四组
- 八进制转二进制
规则:
将八进制数每1位, 转成对应的3位的一个二进制数即可.
案例: 请将 0237 转成 二进制的数
02(010)3(011)7(111) = 0b10011111
- 十六进制转二进制
规则:
将十六进制数每1位, 转成对应的4位的一个二进制数即可.
案例: 请将 0x23B 转成 二进制的数
0x2(0010)3(0011)B(1011) = 0b001000111011
相关文章:

四大进制--详解--以及进制转换规则
进制介绍 对于整数, 有四种表达方式: 二进制BIN: 0,1 , 满2进1.以0b或0B开头 所谓2进制就是使用0和1来表示一个数, 满2进1如果在开发中看到有这种写法: int n1 0b1010; 这种写法没有错, 这是二进制的一种表示方式 十进制DEC: 0-9, 满10进1 十进制就是0-9来表示一个数, 满10进…...

谈谈API和人工智能领域的开发和使用以及AI大模型开发进程。
API,全称为Application Programming Interface,即应用程序编程接口,是一些预先定义的函数。 它的主要目的是提供应用程序与开发人员基于某软件或硬件得以访问一组例程的能力,而无需访问源码,或理解内部工作机制的细节。API函数包含在操作系统的动态连接库文件中,例如Win…...
用Python Pygame做的一些好玩的小游戏
有些游戏的代码比较长就不公布了 1.简简单单 1.疯狂的鸡哥 你要准备的图片: 命名为:ji.png 代码: import pygame import random as r pygame.init() pygame.display.set_caption(aaa) pm pygame.display.set_mode((800,600))class Ls(py…...

【吊打面试官系列】Java高并发篇 - ThreadLocal 是什么?有什么用?
大家好,我是锋哥。今天分享关于 【ThreadLocal 是什么?有什么用?】面试题,希望对大家有帮助; ThreadLocal 是什么?有什么用? ThreadLocal 是一个本地线程副本变量工具类。主要用于将私有线程和该…...
)
Spring MVC的数据转换及数据格式化:java 转换器接口(将一种类型的对象转换为另一种类型及其子类对象)
文章目录 引言I 将String转为BaseEnum的子类对象1.1 注册转换器工厂1.2 实现转换器工厂1.3 实现转换器接口 `interface Converter<S, T> `1.4 根据枚举code和type获取枚举II 枚举2.1 枚举接口2.2 枚举子类2.3 请求实体引言 Spring MVC的数据转换及数据格式化 应用场景:…...
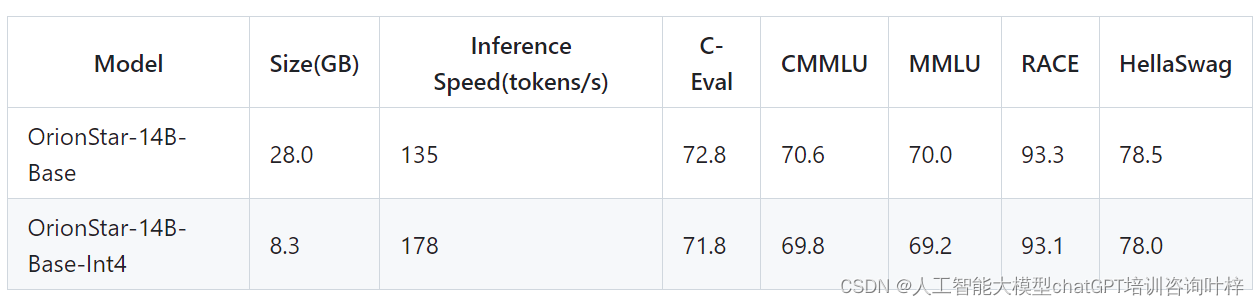
【开源】多语言大型语言模型的革新:百亿参数模型超越千亿参数性能
大型人工智能模型,尤其是那些拥有千亿参数的模型,因其出色的商业应用表现而受到市场的青睐。但是,直接通过API使用这些模型可能会带来数据泄露的风险,尤其是当模型提供商如OpenAI等可能涉及数据隐私问题时。私有部署虽然是一个解决…...

DDL—表—数据类型—日期时间类型相关语法
(1)表格如下: 类型大小范围格式描述DATE31000-01-01 至 9999-12-31YYYY-MM-DD日期值(年月日)TIME3-838:59:59 至 838:59:59HH:MM:SS时间值或持续时间(时分秒)YEAR11901 至 2155YYYY年份值DATET…...
Ant Design pro 6.0.0 搭建使用以及相关配置
一、背景 在选择一款比较合适的中台的情况下,挑选了有arco design、ant design pro、soybean、vue-pure-admin等中台系统,经过筛选就选择了ant design pro。之前使用过arco design 搭建通过组件库拼装过后台管理界面,官方文档也比较全&#…...

Vue生命周期钩子是如何实现的
Vue的生命周期钩子是在Vue组件创建、挂载、更新、销毁等过程中自动调用的特殊函数。这些钩子允许开发者在组件的不同阶段执行特定的逻辑。Vue 2 和 Vue 3 在生命周期钩子上有一些差异,主要是因为Vue 3引入了Composition API和更现代的JavaScript特性。 Vue 2 的生命…...

002 仿muduo库实现高性能服务器组件_整体框架
🌈个人主页:Fan_558 🔥 系列专栏:仿muduo 🌹关注我💪🏻带你学更多知识 文章目录 前言项目框架小结 前言 本文不会包含任何项目模块的代码,旨在向你介绍项目具体分为哪几个模块&am…...

车道线识别与预警系统LDWS(代码+教程)
车道线识别与预警系统(Lane Departure Warning System, LDWS)作为智能交通系统中的重要组成部分,旨在通过先进的图像处理和计算机视觉技术,实时监测车辆行驶过程中的车道位置,预防因驾驶员疏忽或疲劳导致的车道偏离事故…...
——元组)
Python基础学习笔记(七)——元组
目录 一、一维元组的介绍、创建与修改二、组合的基本操作1. 遍历2. 取长度3. 取最值4. 打包5. 批处理5.1 map()函数5.2 lambda 表达式5.3 lambda 表达式 map()函数 一、一维元组的介绍、创建与修改 元组(tuple),一种不可变、有序、可重复的数…...
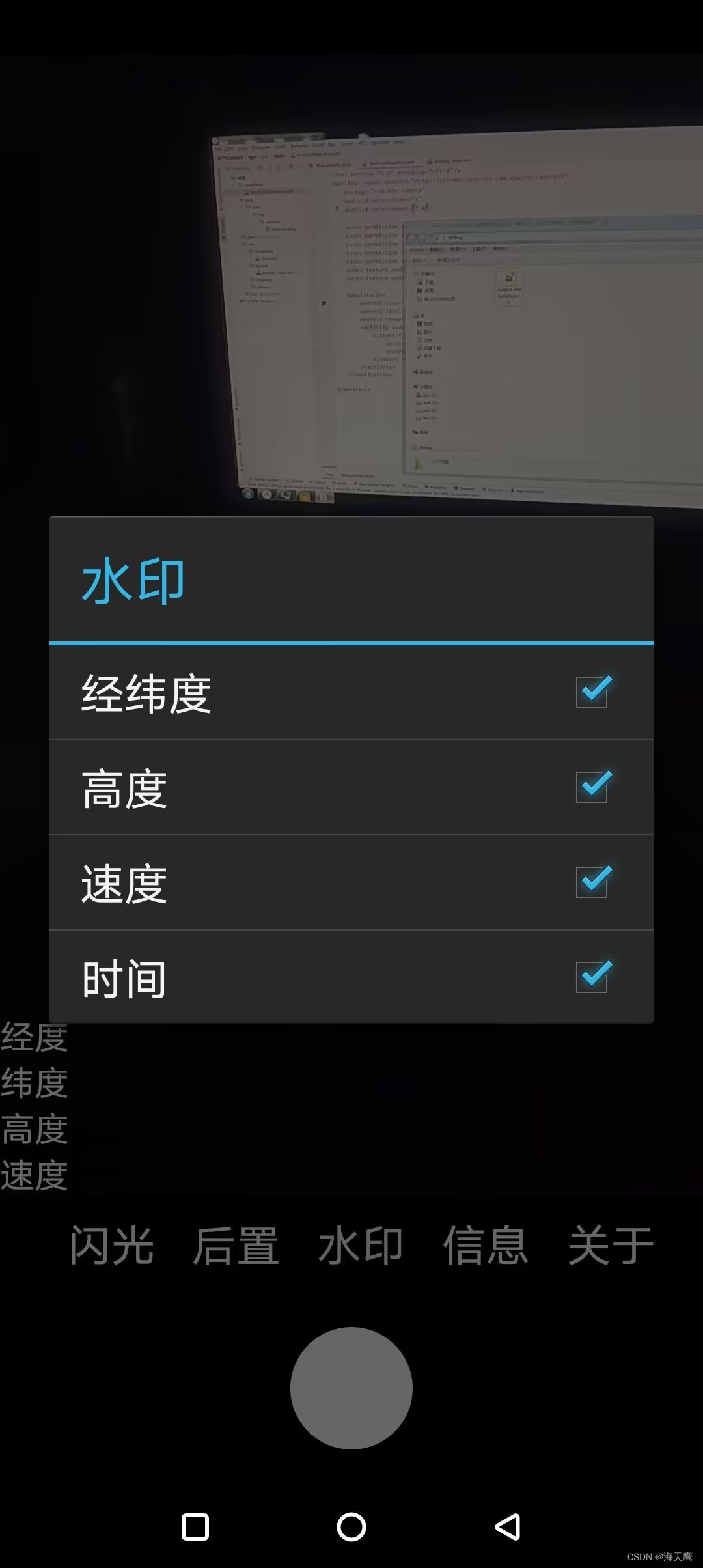
安卓开发:相机水印设置
1.更新水印 DecimalFormat DF new DecimalFormat("#"); DecimalFormat DF1 new DecimalFormat("#.#");LocationManager LM (LocationManager)getSystemService(Context.LOCATION_SERVICE); LM.requestLocationUpdates(LocationManager.GPS_PROVIDER, 2…...

Excel工作表单元格单击选中事件,VBA动态数值排序
Excel工作表单元格单击选中事件,VBA动态数值排序(WX公众号:Excel潘谆白说VBA) 文章目录 前言一、运行效果二、代码前言 面对每月的消费账单,面对月底待还的信用卡或花呗,面对不足三位数的余额,你是否怀疑过账单自己的消费。你是否因此开始记账,每个月记流水,想知道当月…...
数据结构~~链式二叉树
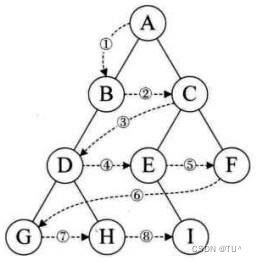
目录 一、基本概念 链式存储概念 二、链式二叉树的结构 链式二叉树结构 构建链式二叉树 二叉树的遍历 二叉树节点和高度等 二叉树销毁 三、链式二叉树的练习 相同的树 对称二叉树 另外一颗子树 二叉树前序遍历 二叉树遍历 四、完整代码 Tree.h Tree.c 五、总结 一…...
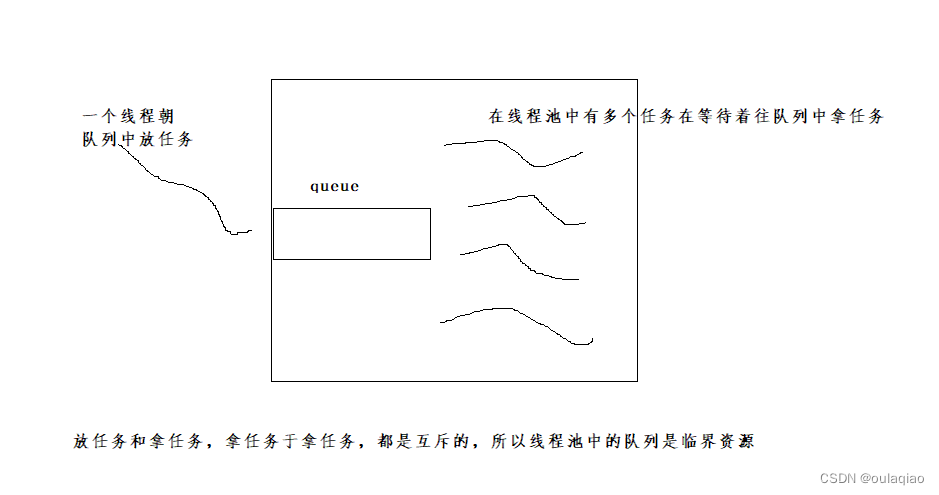
线程池,日志
所要用到的知识点: 多线程的创建 生产消费模型, 线程锁 条件变量 代码: 线程池日志...

vue的图片上传
关于vue3的图片上传,这里记录一下,有兴趣的朋友可以参考。。。。 <van-uploader:after-read"afterRead"v-model"headImg":max-count"1"class"picture"/> const fileList ref();const afterRead (fil…...

题解 P1150
题解 P1150 因为k个烟蒂1根烟1个烟蒂 所以k-1个烟蒂1根烟 注意减掉最后一根烟的烟蒂 (因这题并没有借烟蒂换烟再还回这一说) 此解法为小学4~6年级水平 #include <bits/stdc.h>using namespace std;int main(){int n,k;cin>>n>>k;cout<<n(n-1)/(k-…...

牛客NC324 下一个更大的数(三)【中等 双指针 Java/Go/PHP/C++】参考lintcode 52 · 下一个排列
题目 题目链接: https://www.nowcoder.com/practice/475da0d4e37a481bacf9a09b5a059199 思路 第一步:获取数字上每一个数,组成数组arr 第二步:利用“下一个排列” 问题解题方法来继续作答,步骤:利用lintc…...

Vue3解决“找不到模块“@/components/xxx.vue”或其相应的类型声明”
文章目录 前言背景问题描述解决方案总结 前言 在使用 Vue 3 开发项目时,遇到“找不到模块 ‘/components/xxx.vue’ 或其相应的类型声明”的错误是一个常见问题。这通常与 TypeScript 和模块解析相关的配置不当有关。本文将详细介绍如何解决此问题,确保…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
