第四十五天 | 322.零钱兑换
题目:322.零钱兑换
尝试解答:
1.确定dp[j]含义:装满容量为j的背包所需要放的硬币个数为dp[j];
2.动态转移方程:dp[j] = dp[j - coins[i]] + 1;
3.遍历顺序:本题应该为组合类题目,不考虑装入的顺序,只在乎硬币个数
所以先物品后背包,背包容量从小到大。(错)
4.初始化:dp[0] = 1,其余均初始换为0
5.打印dp
代码实现如下,有漏洞,执行不对:
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, 0);dp[0] = 1;int result = INT_MAX;for(int i = 0; i < coins.size(); i++){for(int j = coins[i]; j <= amount; j++){// dp[j] = dp[j - coins[i]] + 1;// result = min(dp[j], result);if(j == amount){result = min(dp[j], result);}}}return result;}
};正确思路:
1.确定dp[j]含义:装满容量为j的背包所需要最少放的硬币个数为dp[j];
2.动态转移方程:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
本轮要放的物品重量为coins[i],所以背包必须腾出coins[i]这么大的容量留给coins[i],所以之前背包装的重量必须是dp[j - coins[i]]。装了coins[i]后,一共装了dp[j - coins[i]] + 1块硬币,与不装coins[i] 的情况比大小,取其小,得到本轮循环的最优解,就是本次的最少个数。
3.初始化:
本题初始化比较取巧,之前不管是排列还是组合,dp[0]都初始化为了1,但这到题从测试样例中可以看出,dp[0] = 0。
其他位置的值如何进行初始化?从本质入手,因为是取其小,必须将他们初始化为INT_MAX,才可以保证在二维数组的第一行可以成功更改值,不会被原来初始化的值覆盖(解释这一点时我习惯从二维数组的角度出发)。
其实道理和其他题目中,初始化为0的道理是一样的,其他题目如果是取其大max,则初始化为0,只要没有负数的情况,就可以保证能够更新值,不会被覆盖。
4.遍历顺序:
本题对遍历顺序无要求。
首先要分清楚题目类型:本题是求装满背包的最少个数,不是求装满背包有多少种方法,
所以这道题和排列组合无关,对遍历顺序无特殊要求。
只有题目问“方法数”时,才考虑排列还是组合,先背包还是先物品。
5.打印dp
代码如下:
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for(int i = 0; i < coins.size(); i++){ //遍历物品for(int j = coins[i]; j <= amount; j++){ //遍历背包if(dp[j - coins[i]] != INT_MAX){dp[j] = min(dp[j - coins[i]] + 1, dp[j]);}}}if(dp[amount] == INT_MAX) return -1;return dp[amount];}
};对于返回-1的条件不是很理解。
循环里的判断条件:如果dp[j - coins[i]] != INT_MAX,那么是不可能通过目前遍历到的物品将背包装满的。
返回值时进行的判断:如果dp[amount] == INT_MAX,那么不可能将背包装满。
相关文章:

第四十五天 | 322.零钱兑换
题目:322.零钱兑换 尝试解答: 1.确定dp[j]含义:装满容量为j的背包所需要放的硬币个数为dp[j]; 2.动态转移方程:dp[j] dp[j - coins[i]] 1; 3.遍历顺序:本题应该为组合类题目,不考虑装入的顺序&#x…...

3D 生成重建011-LucidDreamer 优化SDS过平滑结果的一种探索
3D 生成重建011-LucidDreamer 优化SDS过平滑结果的一种探索 文章目录 0论文工作1论文方法2 效果 0论文工作 文本到3D生成的最新进展标志着生成模型的一个重要里程碑,为在各种现实场景中创建富有想象力的3D资产打开了新的可能性。虽然最近在文本到3D生成方面的进展…...

ES6 笔记04
01 异步函数的使用 es6推出了一种按照顺序执行的异步函数的方法 async 异步函数 async异步函数可以解决promise封装异步代码,调用时一直then链式编程时比较麻烦的问题 定义异步函数: async function 函数名(){ await 表达式1或者函数的调用1 await 表达式2或者函数的调用2 ...…...
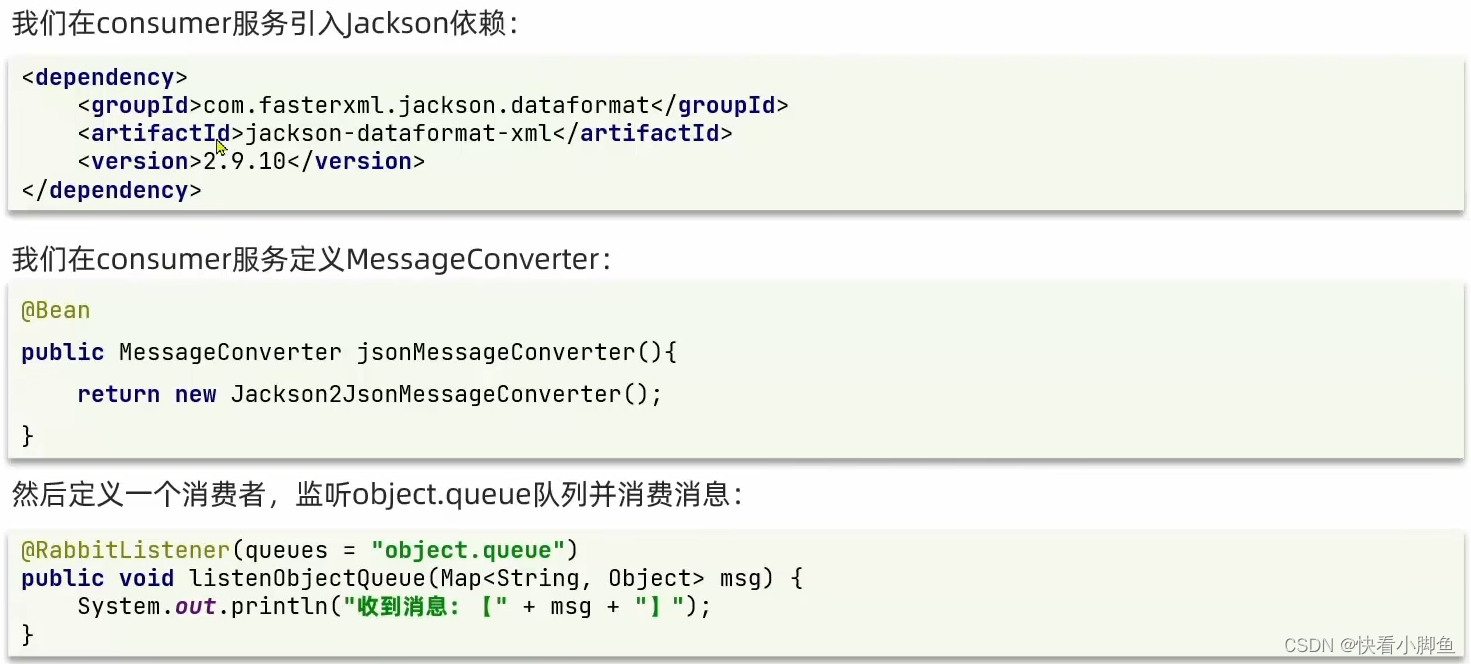
中间件-------RabbitMQ
同步和异步 异步调用 MQ MQ优势:①服务解耦 ②异步调用 ③流量削峰 结构 消息模型 RabbitMQ入门案例,实现消息发送和消息接收 生产者: public class PublisherTest {Testpublic void testSendMessage() throws IOException, TimeoutExce…...

flink Data Source数据源
flink Data Source数据源 Source 并行度 非并行:并行度只能为1 并行 基于集合的Source fromElements package com.pxj.sx.flink; import org.apache.flink.configuration.Configuration; import org.apache.flink.configuration.RestOptions; import org.ap…...

网络七层模型与云计算中的网络服务
网络七层模型,也称为OSI(Open System Interconnection)模型,是由国际标准化组织(ISO)制定的一个概念性框架,用于描述网络通信过程中信息是如何被封装、传输和解封装的。这一模型将复杂的网络通信…...

word一按空格就换行怎么办?word文本之间添加空格就换行怎么办?
如上图,无法在Connection和con之间添加空格,一按空格就会自动换行。 第一步:选中文本,打开段落。 第二步:点击中文版式,勾选允许西文在单词中间换行。 确定之后就解决一按空格就自动换行啦!...

Python 遍历字典的方法,你都掌握了吗
Python中的字典是一种非常灵活的数据结构,它允许通过键来存储和访问值。在处理字典时,经常需要遍历字典中的元素,以下是几种常见的遍历字典的方法。 1. 使用 for 循环直接遍历字典的键 字典的键是唯一的,可以直接通过 for 循环来…...
MySQL 8.4.0 LTS 变更解析:I_S 表、权限、关键字和客户端
↑ 关注“少安事务所”公众号,欢迎⭐收藏,不错过精彩内容~ MySQL 8.4.0 LTS 已经发布 ,作为发版模型变更后的第一个长期支持版本,注定要承担未来生产环境的重任,那么这个版本都有哪些新特性、变更,接下来少…...
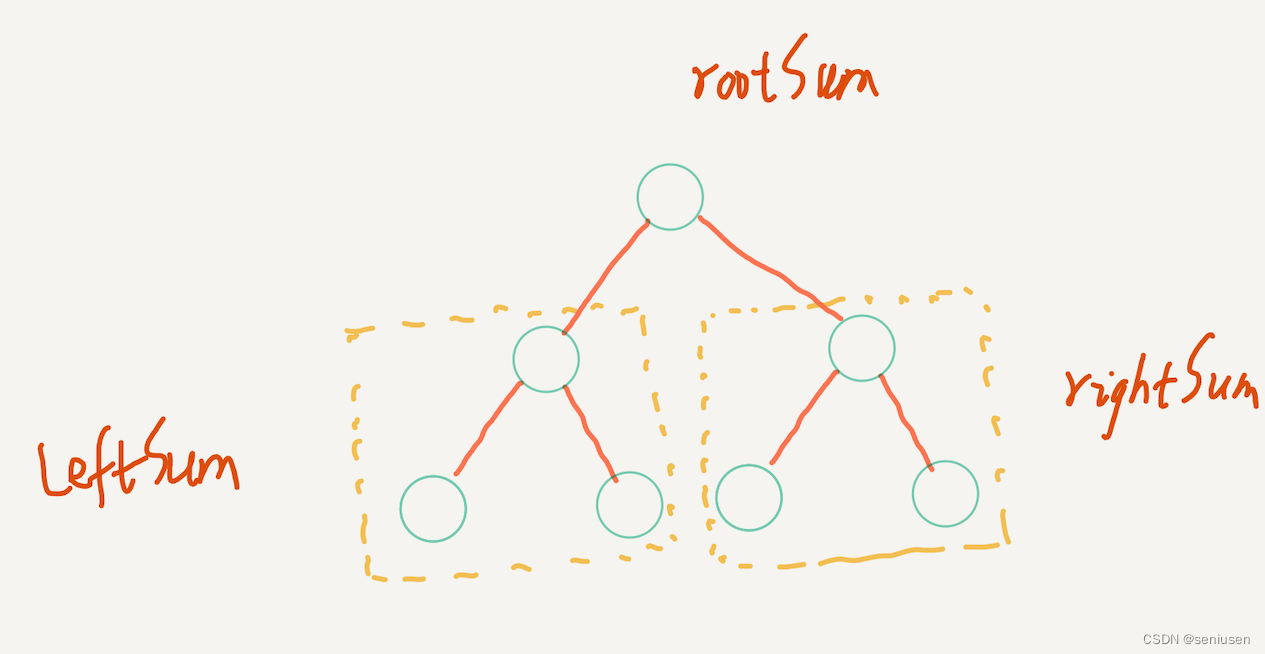
LeetCode 124 —— 二叉树中的最大路径和
阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路 二叉树的问题首先我们要想想是否能用递归来解决,本题也不例外,而递归的关键是找到子问题。 我们首先来看看一棵最简单的树,也就是示例 1。这样的一棵树总共有六条路径…...

美甲店会员预约系统管理小程序的作用是什么
女性爱美体现在方方面面,美丽好看的指甲也不能少,市场中美甲店、小摊不少,也跑出了不少连锁品牌,70后到00后,每个层级都有不少潜在客户,商家需要获取和完善转化路径,不断提高品牌影响力与自身内…...

..堆..
堆 堆是完全二叉树,即除了最后一列之外,上面的每一层都是满的(左右严格对称且每个节点都满子节点) 最后一列从左向右排序。 默认大根堆:每一个节点都大于其左右儿子,根节点就是整个数据结构的最大值 pr…...
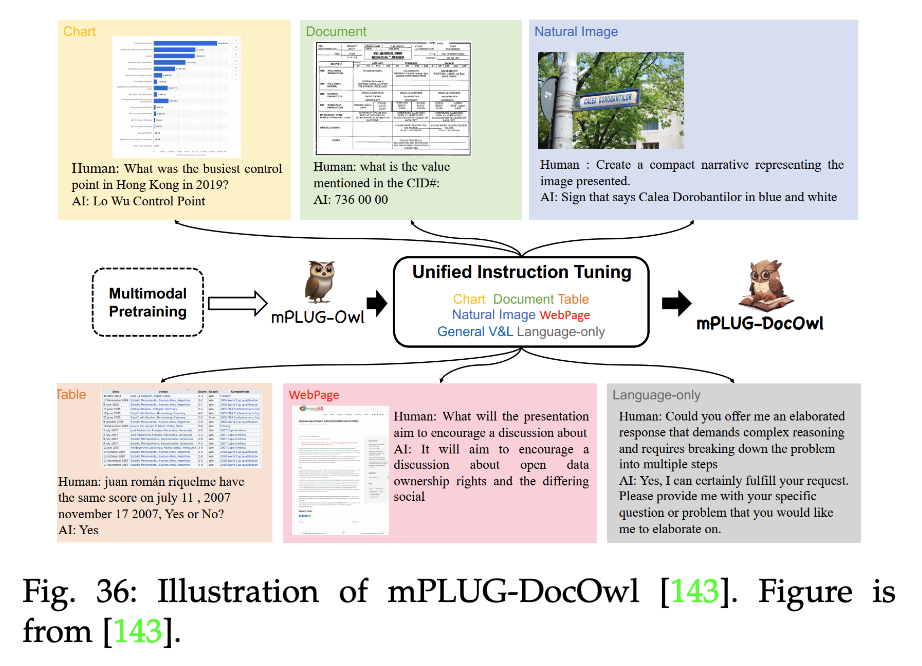
【LLM多模态】综述Visual Instruction Tuning towards General-Purpose Multimodal Model
note 文章目录 note论文1. 论文试图解决什么问题2. 这是否是一个新的问题3. 这篇文章要验证一个什么科学假设4. 有哪些相关研究?如何归类?谁是这一课题在领域内值得关注的研究员?5. 论文中提到的解决方案之关键是什么?6. 论文中的…...

探索Linux中的神奇工具:重定向符的妙用
探索Linux中的神奇工具:重定向符的妙用 在Linux系统中,重定向符是一个强大的工具,用于控制命令的输入和输出,实现数据流的定向。本文将详细介绍重定向符的基本用法和一些实用技巧,帮助读者更好地理解和运用这个功能。…...

Kubernetes 文档 / 概念 / 工作负载 / 工作负载管理 / Job
Kubernetes 文档 / 概念 / 工作负载 / 工作负载管理 / Job 此文档从 Kubernetes 官网摘录 中文地址 英文地址 Job 会创建一个或者多个 Pod,并将继续重试 Pod 的执行,直到指定数量的 Pod 成功终止。 随着 Pod 成功结束,Job 跟踪记录成功完成的…...
办公自动化-Python如何提取Word标题并保存到Excel中?
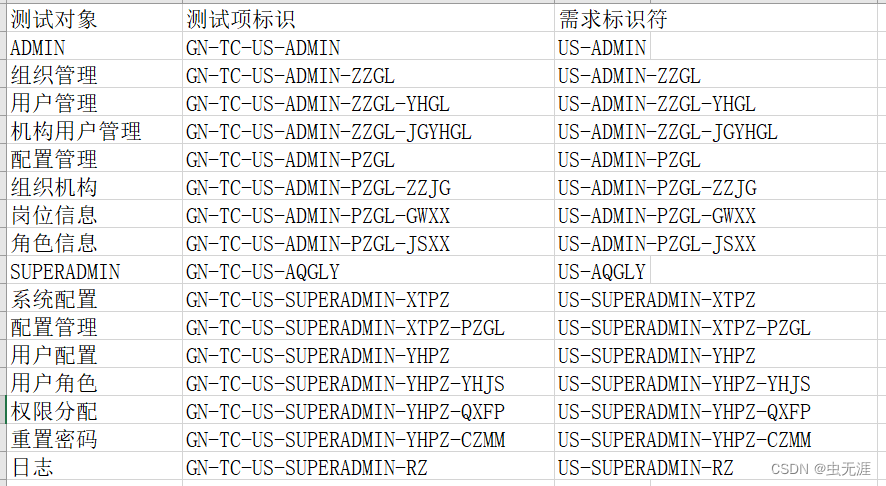
办公自动化-Python如何提取Word标题并保存到Excel中? 应用场景需求分析实现思路实现过程安装依赖库打开需求文件获取word中所有标题去除不需要的标题创建工作簿和工作表分割标题功能名称存入测试对象GN-TC需求标识符存入测试项标识存入需求标识符 完整源码实现效果学…...
基于Java、SpringBoot和uniapp在线考试系统安卓APP和微信小程序
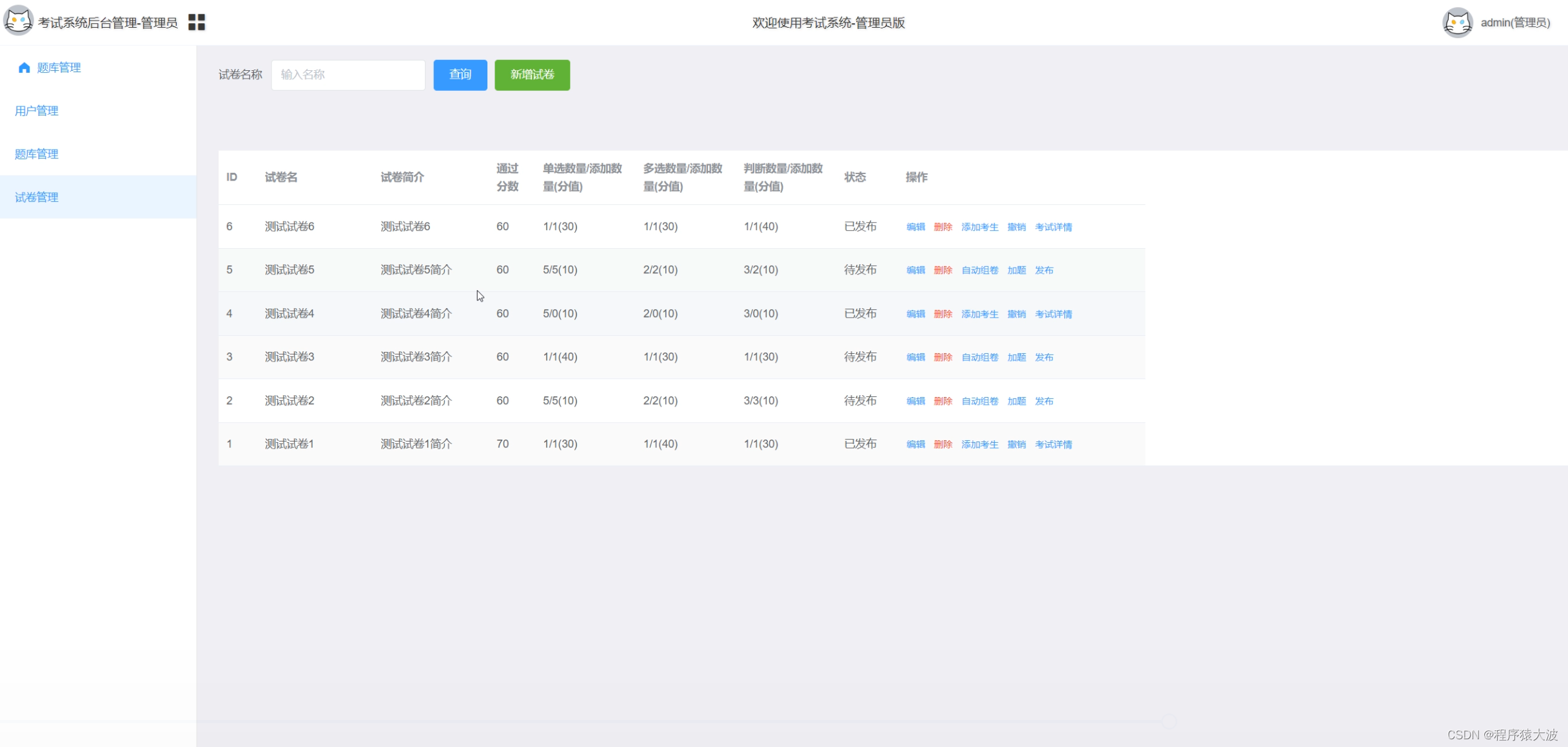
摘要 基于Java、SpringBoot和uniapp的在线考试系统安卓APP微信小程序是一种结合了现代Web开发技术和移动应用技术的解决方案,旨在为教育机构提供一个方便、高效和灵活的在线考试平台。该系统采用Java语言进行后端开发,使用SpringBoot框架简化企业级应用…...
)
抖音a-bogus加密解析(三)
要补的环境我给提示,大家自行操作,出了问题就是因为缺环境,没补好 window global; // reading _u未定义 window.requestAnimationFrame function () {} // XMLHttpRequest 未定义 window.XMLHttpRequest function () {} window.onwheelx …...

IS-IS DIS
原理概述 OSPF 协议支持4种网络类型, IS-IS 协议只支持两种网络类型,即广播网络和点到点网络。与 OSPF 协议相同, IS-IS 协议在广播网络中会将网络视为一个伪节点( Pseudonode ,简称 PSN ),并选举出一台 DIS ( Designa…...

random和range
含义: random(1,10) 不包含10,用于生成随机数。它可以生成浮点数或整数,取决于具体的使用方式。 range(0,1) 不包含1,用于生成一个整数序列。它可以生成一个指定范围内的连续整数序列。 区别在于&#x…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
