打卡信奥刷题(20)用Scratch图形化工具信奥B3756 [信息与未来 2021] 幸运数字
本题的基础是进制转换,关于2进制转换可以参考打卡信奥刷题(19)用Scratch图形化工具信奥B3972 [语言月赛 202405] 二进制 题解
知道了2进制,来实现5进制、7进制、9进制是一样的。
[信息与未来 2021] 幸运数字
题目描述
如果⼀个正整数 n n n 在五进制、七进制、九进制的表⽰下都没有数字 0 0 0,我们就称 n n n 是幸运数字。例如:
-
( 987 ) 10 = ( 12422 ) 5 = ( 2610 ) 7 = ( 1316 ) 9 (987)_{10}=(12422)_5=(2610)_7=(1316)_9 (987)10=(12422)5=(2610)7=(1316)9,因此 n = 987 n=987 n=987 不是幸运数字。
-
( 988 ) 10 = ( 12423 ) 5 = ( 2611 ) 7 = ( 1317 ) 9 (988)_{10}=(12423)_5=(2611)_7=(1317)_9 (988)10=(12423)5=(2611)7=(1317)9,因此 n = 988 n=988 n=988 是幸运数字。
写程序求出 a , a + 1 , a + 2 , ⋯ , b a,a+1,a+2,\cdots,b a,a+1,a+2,⋯,b 之间⼀共有多少个幸运数字。
输入格式
输入一行两个正整数 a a a 和 b b b。
输出格式
输出一行,表示 a , a + 1 , a + 2 , ⋯ , b a,a+1,a+2,\cdots,b a,a+1,a+2,⋯,b 中幸运数字的个数。
样例 #1
样例输入 #1
100 1000
样例输出 #1
203
样例 #2
样例输入 #2
900 4096
样例输出 #2
389
提示
对于 40 % 40\% 40% 的数据, 1 ≤ a ≤ b ≤ 1 0 3 1\leq a \leq b \leq 10^3 1≤a≤b≤103。
对于 100 % 100\% 100% 的数据, 1 ≤ a ≤ b ≤ 1 0 6 1\leq a \leq b \leq 10^6 1≤a≤b≤106。
本题原始满分为 15 pts 15\text{pts} 15pts。
Scratch实现

因为代码有点点多,整个截图截不太完整,我将相关代码上传到csdn,下载地址如下:https://download.csdn.net/download/rogeliu/89359287
接下来我会不断用scratch来实现信奥比赛中的算法题,感兴趣的请关注,我后续将继续分享相关内容
相关文章:

打卡信奥刷题(20)用Scratch图形化工具信奥B3756 [信息与未来 2021] 幸运数字
本题的基础是进制转换,关于2进制转换可以参考打卡信奥刷题(19)用Scratch图形化工具信奥B3972 [语言月赛 202405] 二进制 题解 知道了2进制,来实现5进制、7进制、9进制是一样的。 [信息与未来 2021] 幸运数字 题目描述 如果⼀个…...
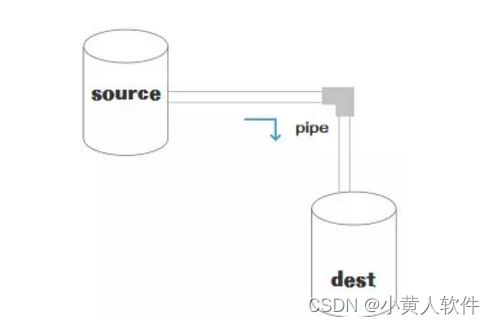
Stream流模式通信及示例
Stream流模式通信是指在计算机网络中,数据作为连续的字节流传输而不是独立的数据包。它是一种面向连接的通信方式,常见于TCP(传输控制协议)。以下是Stream流模式通信的基本概念和一个简单的示例。 基本概念 面向连接࿱…...
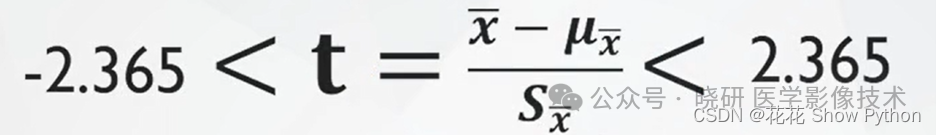
从0开始学统计-t分布
1.t分布是如何被发现的? t分布最早由英国统计学家威廉塞弗顿(William Sealy Gosset)在1908年提出。塞弗顿是爱尔兰的一名酿酒厂的统计学家,他的工作需要对小样本数据进行分析。由于当时样本量较小(通常小于30…...

Git总结超全版
最近想系统的回顾一下Git的使用,如果只想快速的集成git到idea,可以参考另一篇我的博客中的git部分 目录 版本管理工具简介Git安装与配置Git远程仓库配置 Git常用命令为常用命令配置别名(可选)Git忽略文件.gitignore一些概念*本地仓库操作删除仓库内容 *远…...
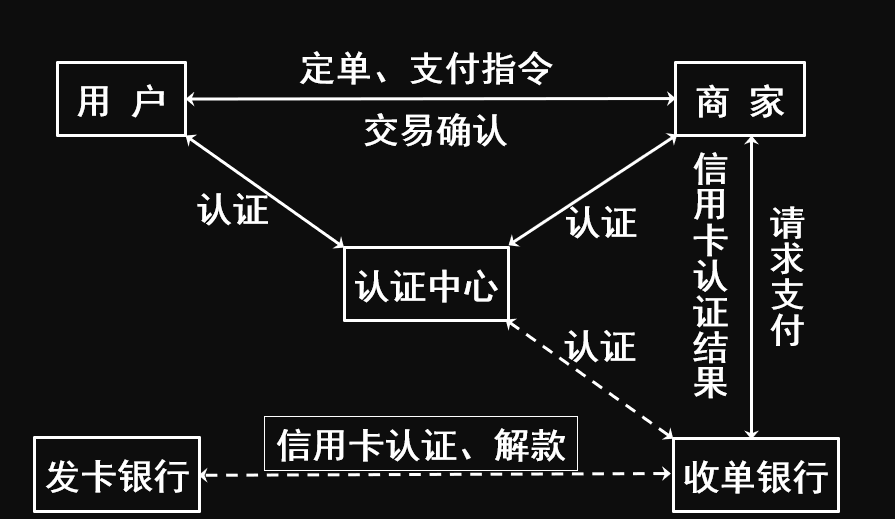
网络安全之安全协议浅谈
安全协议 安全协议概述安全协议分类IPSecIPSec安全协议IPSec架构IPSec封装模式AH协议ESP协议SET协议SET协议电子交易模型SET协议安全目标认证中心CA 安全协议概述 安全协议是信息交换安全的核心,它在网络不同层次上、针对不同应用,通过对各种密码学技术…...

华为云部署前端项目发生的事
今天刚买了一个云服务,想着部署一下前端项目: 使用的是 docker nginx 部署 部署方法,在以往的文章中有介绍,如有兴趣可以看看docker 部署; 结果发现部署成功之后,竟然无法访问,从命令来看&…...

需求:实现一个可以统计代码的运行时间
需求:有一个做加法计算的函数,要统计执行这个加法函数代码运行了多久 import timedef add(a, b):time.sleep(1)return a bst time.time() add(100, 200) et time.time() print("该函数运行时间为:", et - st) 学了闭包&#x…...

软考高级之redis中使用zset实现延迟队列,你答对了么?
实现延迟队列的思路 zset的特性,带有分数的排序,以时间戳作为分数进行排序 添加任务 zdd取出任务 zrangbyscore执行任务 zrem 定时任务 public static void main(String[] args) {Jedis jedis new Jedis("ip", 6379);TimerTask task new …...

CS 下载安装详解
目录 CS简介: CS下载地址: CS的安装: CS简介: CS为目前渗透中常用的一款工具,它的强大在于控制windows木马,CS主要控制windows木马。 CS下载地址: 链接:https://pan.baidu.com/…...
:小地图MiniMap(上))
前端canvas项目实战——在线图文编辑器(十):小地图MiniMap(上)
目录 前言一、 效果展示二、 实现步骤0. 行动前的思考1. 为小地图更新「背景图」2. 为小地图更新「滑动窗口」2.1 获取新的滑动窗口「宽高」2.2 获取新的滑动窗口「位置」3. 为小地图更新「遮罩」后记前言 上一篇博文中,我们引入了「逻辑画布」的概念,让整个工具的页面看起来…...

linux的chmod的数字太难记了,用u, g, o, a更简单!
u, g, o, 和 a是用来设置或查看文件或目录权限在类Unix或Linux系统中的特殊字符,它们分别代表文件或目录的所有者(user)、所属组(group)、其他用户(others)和所有用户(all users)。 而权限方r和w是其中的两种,分别代表读权限(read࿰…...

牛客热题:有效括号
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:有效括号题目链接方法一&#x…...

利用SQL语句实现多表联合查询——多表关系介绍
1.多对多查询 先创建一个student表和course表,应该利用外键来实现,通过一个中间表分别对应student和course中的id CREATE TABLE student (id INT unsigned PRIMARY KEY,name VARCHAR(255),no VARCHAR(50) ); CREATE TABLE course (id INT PRIMARY KEY,…...
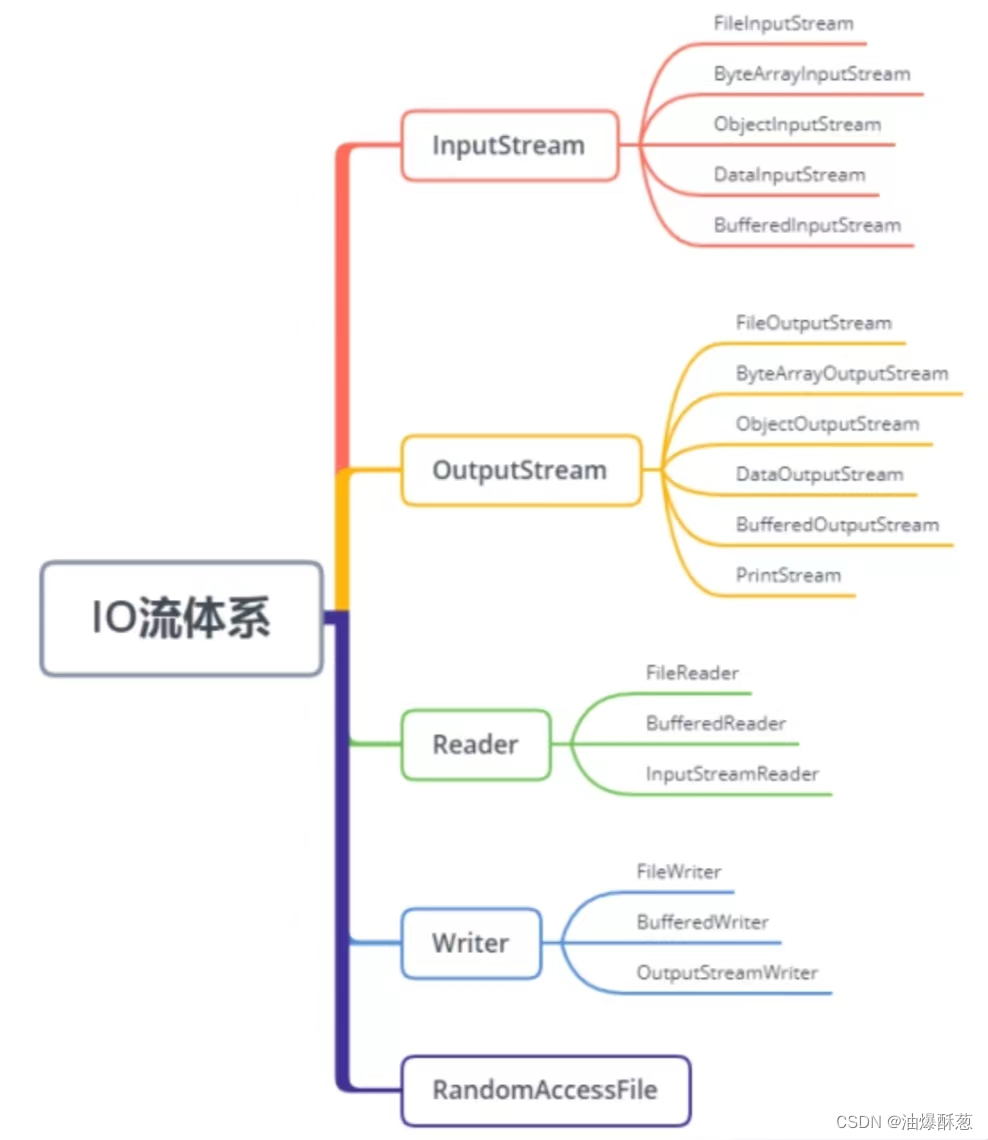
Java中IO流类的体系
Java为我们提供了多种多样的IO流,我们可以根据不同的功能及性能要求挑选合适的IO流,如图所示,为Java中IO流类的体系。 从上图发现,很多流都是成对出现的,比如: FileInputStream/FileOutputStream࿰…...
【调试笔记-20240521-Linux-编译 QEMU/x86_64 可运行的 OpenWrt 固件】
调试笔记-系列文章目录 调试笔记-20240521-Linux-编译 QEMU/x86_64 可运行的 OpenWrt 固件 文章目录 调试笔记-系列文章目录调试笔记-20240521-Linux-编译 QEMU/x86_64 可运行的 OpenWrt 固件 前言一、调试环境操作系统:Ubuntu 22.04.4 LTS编译环境调试目标 二、调…...
)
GitLab的原理及应用详解(六)
本系列文章简介: 随着软件开发的不断进步和发展,版本控制系统成为了现代软件开发过程中不可或缺的一部分。而GitLab作为其中一种流行的版本控制工具,在软件开发领域享有广泛的应用。GitLab不仅提供了强大的版本控制功能,还集成了项…...

【调和级数】100321. 优质数对的总数 II
本文涉及知识点 调和级数 质数、最大公约数、菲蜀定理 LeetCode100321. 优质数对的总数 II 给你两个整数数组 nums1 和 nums2,长度分别为 n 和 m。同时给你一个正整数 k。 如果 nums1[i] 可以被 nums2[j] * k 整除,则称数对 (i, j) 为 优质数对&#…...
 函数式接口)
Java SE入门及基础(54) 函数式接口
目录 1. 什么是函数式接口 函数式接口 示例 示例 2. 函数式编程 示例 3. Lambda 表达式延迟执行 应用场景 示例 4. Consumer 接口 解释说明 示例 5. BiConsumer 接口 解释说明 示例 6. Predicate 接口 解释说明 示例 练习 7. Function 接口 解释说明 示例…...
轻松同步:将照片从三星手机传输到iPad的简便方法
概括 想要在新 iPad 上查看三星照片吗?但是,如果您不知道如何将照片从三星手机传输到 iPad,则无法在 iPad 上查看图片。为此,本文分享了 7 个有用的方法,以便您可以使用它们在不同操作系统之间轻松发送照片。现在&…...

MySQL查询某个字段含有字母数字的值
在MySQL中,要查询某个字段含有字母和数字的值,可以使用正则表达式配合REGEXP操作符。以下是一个详细的示例,说明如何编写这样的查询。 假设我们有一个名为my_table的表,其中有一个名为my_column的字段,我们想要查询这…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
