【调和级数】100321. 优质数对的总数 II
本文涉及知识点
调和级数
质数、最大公约数、菲蜀定理
LeetCode100321. 优质数对的总数 II
给你两个整数数组 nums1 和 nums2,长度分别为 n 和 m。同时给你一个正整数 k。
如果 nums1[i] 可以被 nums2[j] * k 整除,则称数对 (i, j) 为 优质数对(0 <= i <= n - 1, 0 <= j <= m - 1)。
返回 优质数对 的总数。
示例 1:
输入:nums1 = [1,3,4], nums2 = [1,3,4], k = 1
输出:5
解释:
5个优质数对分别是 (0, 0), (1, 0), (1, 1), (2, 0), 和 (2, 2)。
示例 2:
输入:nums1 = [1,2,4,12], nums2 = [2,4], k = 3
输出:2
解释:
2个优质数对分别是 (3, 0) 和 (3, 1)。
提示:
1 <= n, m <= 105
1 <= nums1[i], nums2[j] <= 106
1 <= k <= 103
调和级数
nums1中的元素如果不是k的倍数,删除。是k的倍数, /= k。
cnt1 记录nums1中各元素的数量。
令 max1 = (nums1)
∀ \forall ∀n ∈ \in ∈nums2。 如果n的m倍(m>0) 在nums1中存在,则是优质对。
如果n × \times ×m > max,则无需继续枚举m。
枚举1到y的不超过y的倍数,时间复杂度:y + y/2+y/3 ⋯ \cdots ⋯ 1 就是调和级数,故时间复杂度是:O(ylogy)。
注意:如果nums2有重复元素,则时间复杂度是O(nn)。比如:全部是1。所以:必须用cnt2记录nums2各元素数量。
超时代码
class Solution {
public:long long numberOfPairs(vector<int>& nums1, vector<int>& nums2, int k) {int iMax = *std::max_element(nums1.begin(), nums1.end());vector<int> vCnt1(iMax + 1);for (const auto& n : nums1) {if (0 != n % k) {continue;}vCnt1[n / k]++;}while (vCnt1.size() &&(vCnt1.back() == 0)) {vCnt1.pop_back();}iMax = vCnt1.size() - 1;long long llRet = 0;for (const auto& n : nums2) {for (int tmp = n; tmp <= iMax; tmp += n) {llRet += vCnt1[tmp];}}return llRet;}
};
代码
class Solution {
public:long long numberOfPairs(vector<int>& nums1, vector<int>& nums2, int k) {vector<int> tmp;for (const auto& n : nums1) {if (0 != n % k) { continue; }tmp.emplace_back(n/k);}if (tmp.empty()) { return 0; }int iMax = *std::max_element(tmp.begin(), tmp.end());vector<int> vCnt1(iMax + 1);for (auto& n : tmp) {vCnt1[n]++;}const int iMax2 = *std::max_element(nums2.begin(), nums2.end());vector<long long> vCnt2(iMax2+1);for (auto& n : nums2) {vCnt2[n]++;}long long llRet = 0;for (int i = 1; i <= iMax2; i++ ) {for (int tmp = i; tmp <= iMax; tmp += i) {llRet += vCnt1[tmp]*vCnt2[i];}}return llRet;}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 《喜缺全书算法册》以原理、正确性证明、总结为主。 |
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【调和级数】100321. 优质数对的总数 II
本文涉及知识点 调和级数 质数、最大公约数、菲蜀定理 LeetCode100321. 优质数对的总数 II 给你两个整数数组 nums1 和 nums2,长度分别为 n 和 m。同时给你一个正整数 k。 如果 nums1[i] 可以被 nums2[j] * k 整除,则称数对 (i, j) 为 优质数对&#…...
 函数式接口)
Java SE入门及基础(54) 函数式接口
目录 1. 什么是函数式接口 函数式接口 示例 示例 2. 函数式编程 示例 3. Lambda 表达式延迟执行 应用场景 示例 4. Consumer 接口 解释说明 示例 5. BiConsumer 接口 解释说明 示例 6. Predicate 接口 解释说明 示例 练习 7. Function 接口 解释说明 示例…...
轻松同步:将照片从三星手机传输到iPad的简便方法
概括 想要在新 iPad 上查看三星照片吗?但是,如果您不知道如何将照片从三星手机传输到 iPad,则无法在 iPad 上查看图片。为此,本文分享了 7 个有用的方法,以便您可以使用它们在不同操作系统之间轻松发送照片。现在&…...

MySQL查询某个字段含有字母数字的值
在MySQL中,要查询某个字段含有字母和数字的值,可以使用正则表达式配合REGEXP操作符。以下是一个详细的示例,说明如何编写这样的查询。 假设我们有一个名为my_table的表,其中有一个名为my_column的字段,我们想要查询这…...

通关!游戏设计之道Day14
力量与你同在 所有类型的游戏里,赛车类,解谜类,动作冒险类和射击类你都能找到强化道具。 强化道具 设计强化道具时,设计师应该开动脑筋琢磨下面几个问题 1.强化道具有什么用? 2.他长什么样子,在整个游戏…...

实现一个自定义 hook,用于强制刷新当前组件
写在前面 在 react 中,如果 state 数据发生变化,我们知道,会重新渲染该组件。 但是这个前提是我们需要依赖 state 数据的变化,那比如我们并不想定义 state,又或者说我们的操作不能引起 state 的变化,此时…...

牛客热题:滑动窗口的最大值
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:滑动窗口的最大值题目链接方法一…...

Adobe产品安装目录修改
进入安装包目录,进入到products文件夹 编辑driver.xml文件 将“InstallDir”修改为你需要安装的软件的目录,我这里是修改到D:\Adobe目录 <DriverInfo> <ProductInfo> xxxxxxxxxxxxxxxxx </ProductInfo> 拷贝RequestInfo这部分…...
时间(空间)复杂度(结构篇)
目录 前言: 一、时间复杂度 1.1 时间复杂度的定义 1.2 时间复杂度的分析 表示方法: 1.3 常见的时间复杂度 1.4 时间复杂度的计算以及简单的分析 冒泡排序 折半查找(二分查找) 斐波那契数列(递归)…...

react记录部署
导语 React中的核心概念 1 虚拟DOM(Virtual DOM) 2 Diff算法(虚拟DOM的加速器,提升React性能的法宝) React主要的原理 Virtual DOM 虚拟DOM; 提供了一种不同的而又强大的方式来更新DOM, 代替直接的DOM操…...
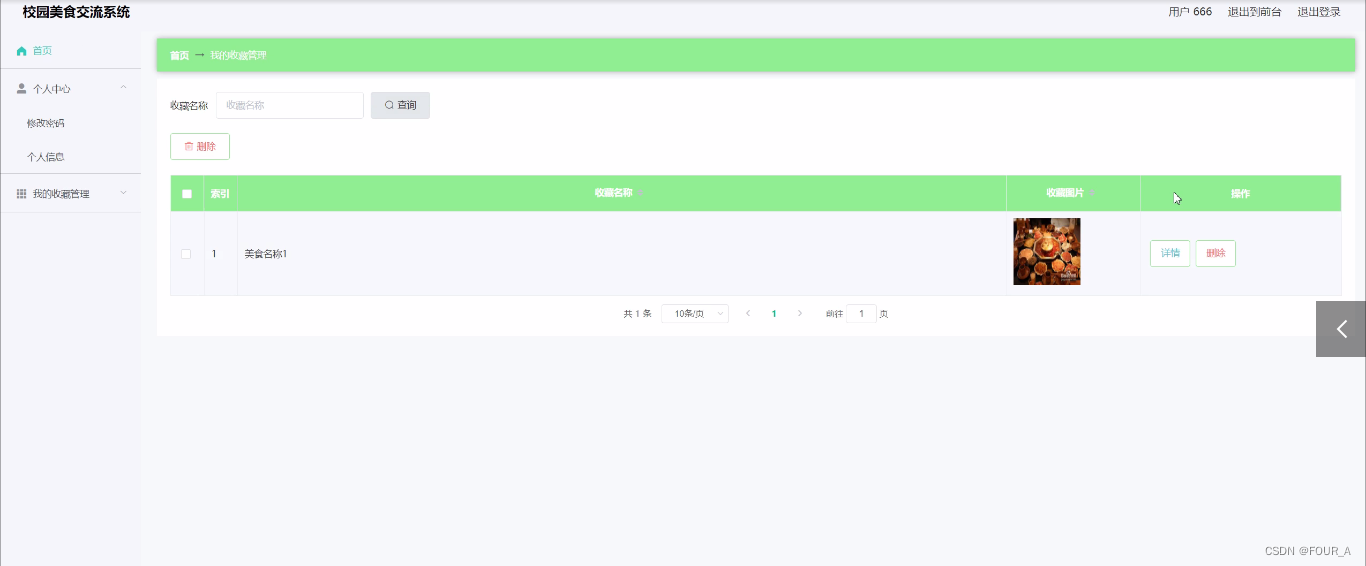
【计算机毕业设计】基于SSM+Vue的校园美食交流系统【源码+lw+部署文档】
目录 前 言 第1章 概述 1.1 研究背景 1.2 研究目的 1.3 研究内容 第二章 开发技术介绍 2.1 Java技术 2.2 Mysql数据库 2.3 B/S结构 2.4 SSM框架 第三章 系统分析 3.1 可行性分析 3.1.1 技术可行性 3.1.2 经济可行性 3.1.3 操作可行性 3.2 系统性能分析 3.3 系…...
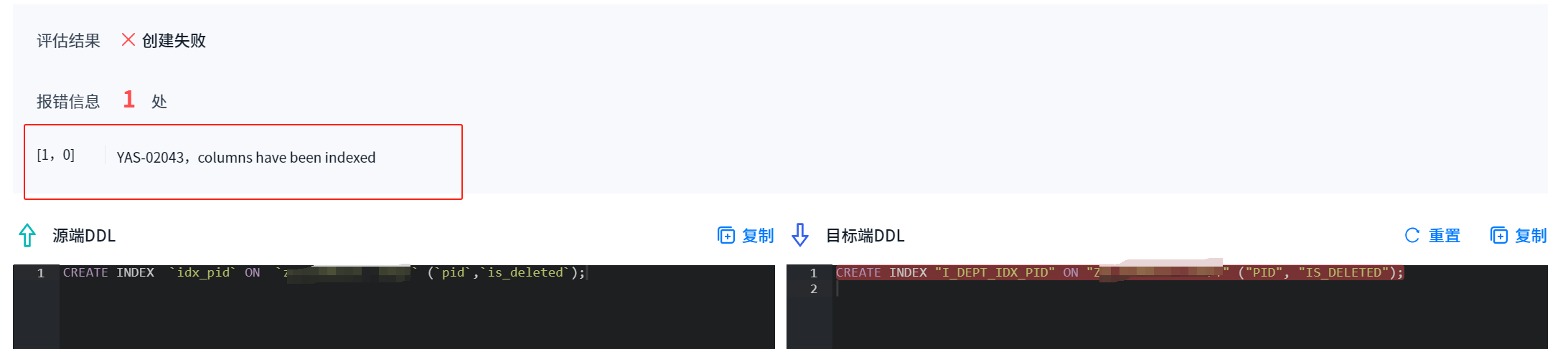
「YashanDB迁移体验官」Mysql生产环境迁移至YashanDB数据库深度体验
「YashanDB迁移体验官」Mysql生产环境迁移至YashanDB数据库深度体验 1. 前言1.1 产品介绍1.2 产品架构1.3 产品规格1.3.1 数据库版本支持1.3.2 数据类型支持 2. YMP安装2.1 环境说明2.2 执行安装2.3 访问YMP2.3.1 YMP登录界面2.3.2 YMP迁移流程 3. YMP数据迁移3.1 创建数据源3.…...

qmt量化交易策略小白学习笔记第4期【qmt如何获取获取行情数据--内置python使用方法】
内置python使用方法 qmt更加详细的教程方法,会持续慢慢梳理。 也可找寻博主的历史文章,搜索关键词查看解决方案 ! 感谢关注,需免费开通量化回测与咨询实盘权限,可以和博主联系! 获取历史行情与实时行情…...

XXE(XML外部实体注入)
1、XXE原理 XXE(XML外部实体注入,XML External Entity) ,在应用程序解析XML输入时,当允许引用外部实体时,可构造恶意内容,导致读取任意文件、探测内网端口、攻击内网网站、发起DoS拒绝服务攻击、执行系统命…...

kafka 案例
kafka 案例 目录概述需求: 设计思路实现思路分析1.kafka案例_API 带回调函数的生产者2.kafka案例_API生产者分区策略测试3.kafka案例_自定义分区的生产者4.kafka案例_API同步发送生产者5.kafka案例_API简单消费者5.kafka案例_API消费者重置offset 参考资料和推荐阅读…...

别被“涨价“带跑,性价比才是消费真理
文章来源:全食在线 “再不好好赚钱,连方便面也吃不起了。”这是昨天在热搜下,一位网友的留言。而热搜的内容,正是康师傅方便面即将涨价的消息。 01 传闻初现 昨天上午,朋友圈就有人放出康师傅方便面要涨价的消息&am…...

GEE深度学习——使用Tensorflow进行神经网络DNN土地分类
Tensorflow TensorFlow是一个开源的深度学习框架,由Google开发和维护。它提供了一个灵活的框架来构建和训练各种机器学习模型,尤其是深度神经网络模型。 TensorFlow的主要特点包括: 1. 它具有高度的灵活性,可以用于训练和部署各种类型的机器学习模型,包括分类、回归、聚…...
)
死锁示例(python、go)
Thread 1首先获取了资源A,然后尝试获取资源B,但此时资源B已经被Thread 2获取,因此Thread 1会一直等待。而Thread 2也类似,首先获取资源B,然后尝试获取资源A,但此时资源A已经被Thread 1获取,因此…...
)
Spring Cloud 面试题(五)
1. Eureka的自我保护模式是什么? Eureka的自我保护模式是一种应对网络异常的安全保护措施,旨在防止因网络分区或其他异常情况导致服务实例被错误地注销。当Eureka Server在短时间内丢失过多的客户端心跳时,会触发自我保护机制。以下是自我保…...
源码编译安装LAMP
1.LAMP介绍 LAMP架构是目前成熟的企业网站应用模式之一,指的是协同工作的一整套系统和相关软件,能够提供动态Web站点服务及其应用开发环境。LAMP是一个缩写词,具体包括Linux操作系统、Apache网站服务器、MySQL数据库服务器、PHP(…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
