时间(空间)复杂度(结构篇)
目录
前言:
一、时间复杂度
1.1 时间复杂度的定义
1.2 时间复杂度的分析
表示方法:
1.3 常见的时间复杂度
1.4 时间复杂度的计算以及简单的分析
冒泡排序
折半查找(二分查找)
斐波那契数列(递归)
二、空间复杂度
2.1 空间复杂度的定义
2.2 空间复杂度的分析
2.3 常见的空间复杂度
2.4 空间复杂度的计算以及简单分析
冒泡排序
斐波那契数列(迭代)
复杂度是计算机科学中的一个基础概念,它帮助我们理解和评估算法的效率,对于算法设计和优化至关重要。算法的复杂度通常分为时间复杂度和空间复杂度两个方面。
前言:
众所周知:程序 = 算法 + 数据结构;衡量一个算法的标准就是算法效率。那么,算法效率是指算法执行的时间和所需的存储空间。在计算机科学中,算法效率通常通过时间复杂度和空间复杂度来衡量。
一、时间复杂度
1.1 时间复杂度的定义
- 时间复杂度是衡量算法执行时间随输入规模增长而变化的度量,它指示了算法的效率和性能。
- 时间复杂度通常使用大O符号(O)来表示,表示算法执行时间的上界。
- 时间复杂度描述的是算法执行时间与输入规模的增长趋势,而不是具体的执行时间。
1.2 时间复杂度的分析
表示方法:
大O 的表示法:是用于描述函数渐进行为的数学符号。
算法中的基本操作的执行次数,为算法 的时间复杂度。随着问题规模 n 的伴随某个函数f(n)变话记作:
- 一般的忽略常数项。
- 只保留最高次幂项。
注意:我们通常表示的是一个数量级,而不是具体值或某个函数。
1.3 常见的时间复杂度
- 常数时间复杂度:O(1),表示算法的执行时间不随输入规模的增长而变化,是最理想的情况。
- 对数时间复杂度:O(log n),通常出现在二分查找等分治算法中。
- 线性时间复杂度:O(n),表示算法的执行时间与输入规模成正比。
- 线性对数时间复杂度:O(n log n),通常出现在快速排序、归并排序等分治算法中。
- 平方时间复杂度:O(n^2),通常出现在嵌套循环的算法中。
- 指数时间复杂度:O(2^n),通常出现在递归算法中。
- 多项式时间复杂度:O(n^k),k可能是大于 2 的正整数,这意味着算法在大规模数据上的性能下降较快。
1.4 时间复杂度的计算以及简单的分析
通过分析算法中基本操作的执行次数,并根据输入规模的增长情况确定时间复杂度。
三种情况:
- 最好时间复杂度
- 平均时间复杂度
- 最坏时间复杂度
冒泡排序
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}分析:冒泡排序的时间复杂度:O(N^2)
解释:有N个个数,每次移动N-1次,剩下(N-1)移动(N-2)次,总共执行(N*(N-1)/2)次,根据大O表示就是:
折半查找(二分查找)
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin < end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid;elsereturn mid;}return -1;
}分析:折半查找的时间复杂度:最好是O( 1 ) ,最坏是O( log N ) ,该式表示:以2为底N的对数(仅限在计算机中表示)
解释:在查找的时候每次折半,也就是除以 2,一次是2^1,两次是 2^2,推广到N次数。
斐波那契数列(递归)
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
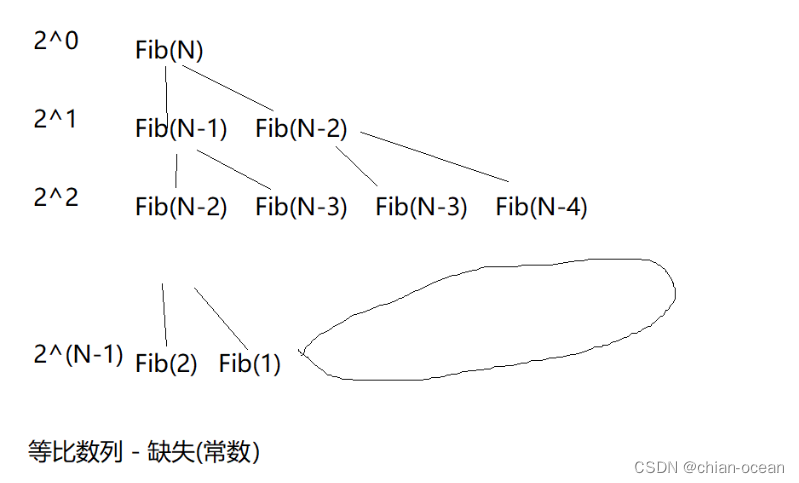
}分析:斐波那契数列时间复杂度:O(2^n)
解释:
二、空间复杂度
2.1 空间复杂度的定义
- 空间复杂度(Space Complexity)是衡量算法在执行过程中临时占用存储空间大小的量度。
- 它反映了算法所需存储空间与输入数据大小之间的关系。
- 空间复杂度通常用大O表示法来表示。
2.2 空间复杂度的分析
同时间复杂度一样用大O表示法表示;也是表示一个数量级。记作:
2.3 常见的空间复杂度
- 常数阶:如果算法的空间复杂度不随问题规模 n 的变化而变化,即算法所需的存储空间是一个常数,那么空间复杂度为 O(1)。
- 线性阶:如果算法所需的存储空间与问题规模 n 成正比,即算法所需的存储空间随着 n 的增加而线性增加,那么空间复杂度为 O(n)。
- 多项式阶:如果算法所需的存储空间与问题规模 n 的关系可以表示为多项式函数,即空间复杂度为 O(n^k),其中 k 是一个正整数。
- 对数阶:如果算法所需的存储空间与问题规模 n 的关系可以表示为对数函数,即空间复杂度为 O(log n)。
- 指数阶:如果算法所需的存储空间与问题规模 n 的关系可以表示为指数函数,即空间复杂度为 O(2^n)。
2.4 空间复杂度的计算以及简单分析
计算空间复杂度时,需要考虑算法在运行过程中显式申请的额外空间,而不是函数运行时所需要的栈空间,后者在编译期间已经确定好了
冒泡排序
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}分析:冒泡排序空间复杂度:O(1)
解释:仅仅使用了一个额外变量。
斐波那契数列(迭代)
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}分析:斐波那契数列空间复杂度:O( N )
解释:开辟了N个空间。
相关文章:
时间(空间)复杂度(结构篇)
目录 前言: 一、时间复杂度 1.1 时间复杂度的定义 1.2 时间复杂度的分析 表示方法: 1.3 常见的时间复杂度 1.4 时间复杂度的计算以及简单的分析 冒泡排序 折半查找(二分查找) 斐波那契数列(递归)…...

react记录部署
导语 React中的核心概念 1 虚拟DOM(Virtual DOM) 2 Diff算法(虚拟DOM的加速器,提升React性能的法宝) React主要的原理 Virtual DOM 虚拟DOM; 提供了一种不同的而又强大的方式来更新DOM, 代替直接的DOM操…...
【计算机毕业设计】基于SSM+Vue的校园美食交流系统【源码+lw+部署文档】
目录 前 言 第1章 概述 1.1 研究背景 1.2 研究目的 1.3 研究内容 第二章 开发技术介绍 2.1 Java技术 2.2 Mysql数据库 2.3 B/S结构 2.4 SSM框架 第三章 系统分析 3.1 可行性分析 3.1.1 技术可行性 3.1.2 经济可行性 3.1.3 操作可行性 3.2 系统性能分析 3.3 系…...
「YashanDB迁移体验官」Mysql生产环境迁移至YashanDB数据库深度体验
「YashanDB迁移体验官」Mysql生产环境迁移至YashanDB数据库深度体验 1. 前言1.1 产品介绍1.2 产品架构1.3 产品规格1.3.1 数据库版本支持1.3.2 数据类型支持 2. YMP安装2.1 环境说明2.2 执行安装2.3 访问YMP2.3.1 YMP登录界面2.3.2 YMP迁移流程 3. YMP数据迁移3.1 创建数据源3.…...

qmt量化交易策略小白学习笔记第4期【qmt如何获取获取行情数据--内置python使用方法】
内置python使用方法 qmt更加详细的教程方法,会持续慢慢梳理。 也可找寻博主的历史文章,搜索关键词查看解决方案 ! 感谢关注,需免费开通量化回测与咨询实盘权限,可以和博主联系! 获取历史行情与实时行情…...

XXE(XML外部实体注入)
1、XXE原理 XXE(XML外部实体注入,XML External Entity) ,在应用程序解析XML输入时,当允许引用外部实体时,可构造恶意内容,导致读取任意文件、探测内网端口、攻击内网网站、发起DoS拒绝服务攻击、执行系统命…...

kafka 案例
kafka 案例 目录概述需求: 设计思路实现思路分析1.kafka案例_API 带回调函数的生产者2.kafka案例_API生产者分区策略测试3.kafka案例_自定义分区的生产者4.kafka案例_API同步发送生产者5.kafka案例_API简单消费者5.kafka案例_API消费者重置offset 参考资料和推荐阅读…...

别被“涨价“带跑,性价比才是消费真理
文章来源:全食在线 “再不好好赚钱,连方便面也吃不起了。”这是昨天在热搜下,一位网友的留言。而热搜的内容,正是康师傅方便面即将涨价的消息。 01 传闻初现 昨天上午,朋友圈就有人放出康师傅方便面要涨价的消息&am…...

GEE深度学习——使用Tensorflow进行神经网络DNN土地分类
Tensorflow TensorFlow是一个开源的深度学习框架,由Google开发和维护。它提供了一个灵活的框架来构建和训练各种机器学习模型,尤其是深度神经网络模型。 TensorFlow的主要特点包括: 1. 它具有高度的灵活性,可以用于训练和部署各种类型的机器学习模型,包括分类、回归、聚…...
)
死锁示例(python、go)
Thread 1首先获取了资源A,然后尝试获取资源B,但此时资源B已经被Thread 2获取,因此Thread 1会一直等待。而Thread 2也类似,首先获取资源B,然后尝试获取资源A,但此时资源A已经被Thread 1获取,因此…...
)
Spring Cloud 面试题(五)
1. Eureka的自我保护模式是什么? Eureka的自我保护模式是一种应对网络异常的安全保护措施,旨在防止因网络分区或其他异常情况导致服务实例被错误地注销。当Eureka Server在短时间内丢失过多的客户端心跳时,会触发自我保护机制。以下是自我保…...
源码编译安装LAMP
1.LAMP介绍 LAMP架构是目前成熟的企业网站应用模式之一,指的是协同工作的一整套系统和相关软件,能够提供动态Web站点服务及其应用开发环境。LAMP是一个缩写词,具体包括Linux操作系统、Apache网站服务器、MySQL数据库服务器、PHP(…...
html5网页-浏览器中实现高德地图定位功能
介绍 HTML5是当前Web开发中最常用的技术之一,而地图应用又是其中一个非常常见的需求。高德地图是国内最受欢迎的地图服务提供商之一,他们提供了一系列的API,方便开发者在自己的网站或应用中集成地图功能。 接下来我们如何使用HTML5浏览器和高…...
C从零开始实现贪吃蛇大作战
个人主页:星纭-CSDN博客 系列文章专栏 : C语言 踏上取经路,比抵达灵山更重要!一起努力一起进步! 有关Win32API的知识点在上一篇文章: 目录 一.地图 1.控制台基本介绍 2.宽字符 1.本地化 2.类项 3.setlocale函…...

国内外相机在LabVIEW图像处理的对比
概述 本文对比国内外相机在LabVIEW进行图像处理的区别,探讨各自的特点。国内相机如大恒和海康威视,具有较高性价比和本地化支持;国外品牌如Basler和FLIR则以高性能和稳定性著称。两者在驱动兼容性、图像质量和技术支持方面各有优势。 详细对…...

第四十五天 | 322.零钱兑换
题目:322.零钱兑换 尝试解答: 1.确定dp[j]含义:装满容量为j的背包所需要放的硬币个数为dp[j]; 2.动态转移方程:dp[j] dp[j - coins[i]] 1; 3.遍历顺序:本题应该为组合类题目,不考虑装入的顺序&#x…...

3D 生成重建011-LucidDreamer 优化SDS过平滑结果的一种探索
3D 生成重建011-LucidDreamer 优化SDS过平滑结果的一种探索 文章目录 0论文工作1论文方法2 效果 0论文工作 文本到3D生成的最新进展标志着生成模型的一个重要里程碑,为在各种现实场景中创建富有想象力的3D资产打开了新的可能性。虽然最近在文本到3D生成方面的进展…...

ES6 笔记04
01 异步函数的使用 es6推出了一种按照顺序执行的异步函数的方法 async 异步函数 async异步函数可以解决promise封装异步代码,调用时一直then链式编程时比较麻烦的问题 定义异步函数: async function 函数名(){ await 表达式1或者函数的调用1 await 表达式2或者函数的调用2 ...…...
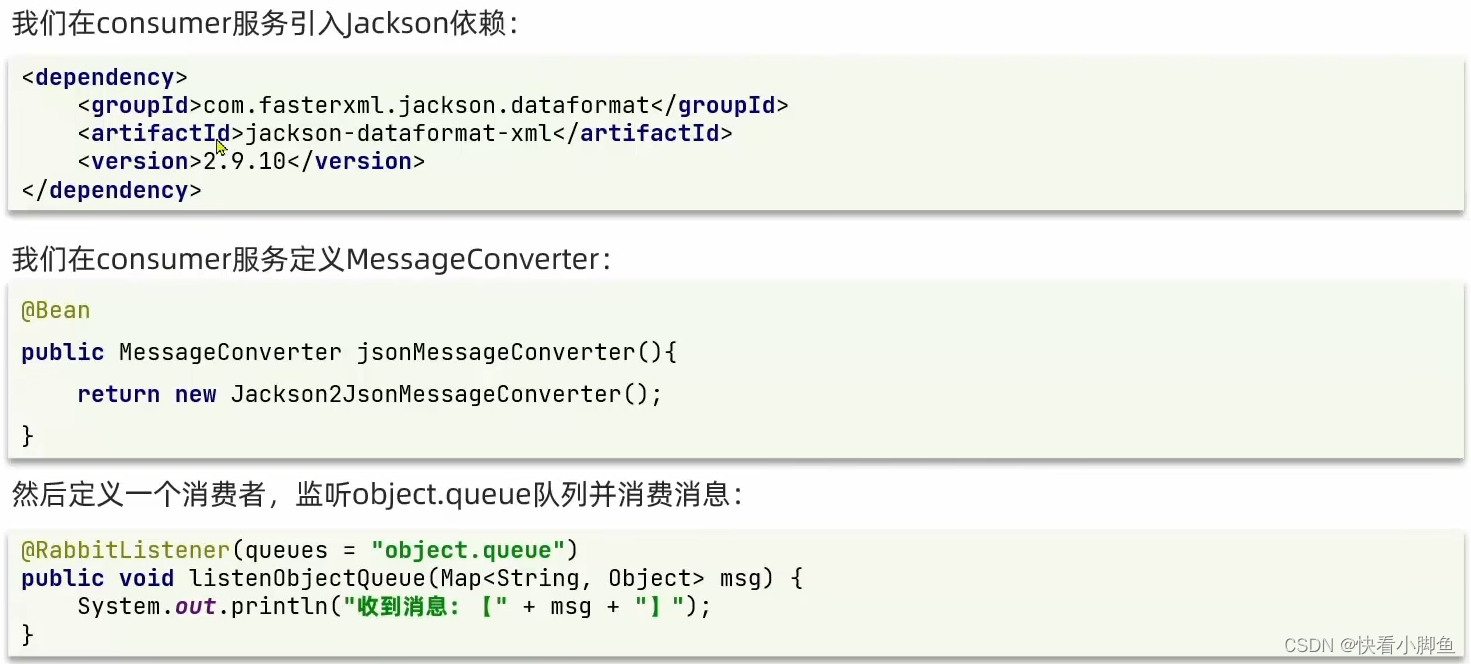
中间件-------RabbitMQ
同步和异步 异步调用 MQ MQ优势:①服务解耦 ②异步调用 ③流量削峰 结构 消息模型 RabbitMQ入门案例,实现消息发送和消息接收 生产者: public class PublisherTest {Testpublic void testSendMessage() throws IOException, TimeoutExce…...

flink Data Source数据源
flink Data Source数据源 Source 并行度 非并行:并行度只能为1 并行 基于集合的Source fromElements package com.pxj.sx.flink; import org.apache.flink.configuration.Configuration; import org.apache.flink.configuration.RestOptions; import org.ap…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
