探索集合python(Set)的神秘面纱:它与字典有何不同?

新书上架~👇全国包邮奥~

python实用小工具开发教程![]() http://pythontoolsteach.com/3
http://pythontoolsteach.com/3
欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~
目录
一、集合(Set)与字典(Dictionary)的初识
1. 集合的无序性
2. 集合的唯一性
二、集合的内部实现原理
1. 哈希函数的作用
2. 冲突解决
三、集合的使用场景与示例
1. 去除重复元素
2. 交集、并集和差集运算

一、集合(Set)与字典(Dictionary)的初识
在编程的世界里,字典和集合都是常见的数据结构,但它们的用途和特点却大不相同。就像字典为我们提供了键值对的存储方式,集合则以其独特的无序性和唯一性著称。
1. 集合的无序性
与字典不同,集合并不保证元素的顺序。这意味着,当你向集合中添加元素时,这些元素在集合中的位置可能会因各种因素而改变。但正是这种无序性,使得集合在处理一些不需要特定顺序的场景时,表现出更高的效率。
2. 集合的唯一性
集合的另一个显著特点是元素的唯一性。在集合中,每个元素只能出现一次。这意味着,如果你尝试向集合中添加一个已经存在的元素,该操作将被忽略。这种特性使得集合在去除重复元素时非常有用。
二、集合的内部实现原理
集合和字典在内部实现上都依赖于哈希表(Hash Table)。哈希表是一种通过哈希函数将键(Key)映射到值(Value)的数据结构。在集合中,哈希函数被用来将元素映射到存储位置,从而实现快速的查找和插入操作。
1. 哈希函数的作用
哈希函数在集合中起着至关重要的作用。它通过计算元素的哈希值,将元素映射到哈希表的特定位置。这样,当需要查找或插入元素时,只需计算其哈希值,即可快速定位到相应的存储位置。
2. 冲突解决
然而,哈希函数并不是完美的。有时,不同的元素可能会计算出相同的哈希值,从而导致哈希冲突。为了解决这个问题,集合(以及字典)采用了各种冲突解决策略,如链地址法、开放地址法等。这些策略能够有效地处理哈希冲突,保证集合的正常运行。
三、集合的使用场景与示例
集合在实际编程中有着广泛的应用场景。下面,我们将通过一些示例来说明集合的用途。
1. 去除重复元素
假设你有一个包含重复元素的列表,你可以使用集合来轻松地去除这些重复元素。例如,你可以使用Python的set()函数将列表转换为集合,从而去除重复元素。以下是一个简单的示例:
# 原始列表,包含重复元素
original_list = [1, 2, 3, 2, 4, 5, 5, 6] # 将列表转换为集合,去除重复元素
unique_set = set(original_list) # 将集合转换回列表(如果需要)
unique_list = list(unique_set) print(unique_list) # 输出:[1, 2, 3, 4, 5, 6]2. 交集、并集和差集运算
集合还支持交集、并集和差集等运算。这些运算在处理多个集合之间的关系时非常有用。以下是一些示例:
# 定义两个集合
set1 = {1, 2, 3, 4}
set2 = {3, 4, 5, 6} # 交集运算
intersection = set1 & set2
print(intersection) # 输出:{3, 4} # 并集运算
union = set1 | set2
print(union) # 输出:{1, 2, 3, 4, 5, 6} # 差集运算(set1中有但set2中没有的元素)
difference = set1 - set2
print(difference) # 输出:{1, 2}通过这些示例,我们可以看到集合在编程中的强大功能和灵活性。无论是去除重复元素还是进行集合运算,集合都能为我们提供高效且简洁的解决方案。
非常感谢您花时间阅读我的博客,希望这些分享能为您带来启发和帮助。期待您的反馈与交流,让我们共同成长,再次感谢!
👇热门内容👇
python使用案例与应用_安城安的博客-CSDN博客
软硬件教学_安城安的博客-CSDN博客
Orbslam3&Vinsfusion_安城安的博客-CSDN博客
网络安全_安城安的博客-CSDN博客
教程_安城安的博客-CSDN博客
python办公自动化_安城安的博客-CSDN博客
👇个人网站👇
安城安的云世界

相关文章:

探索集合python(Set)的神秘面纱:它与字典有何不同?
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、集合(Set)与字典(Dictionary)的初识 1. …...
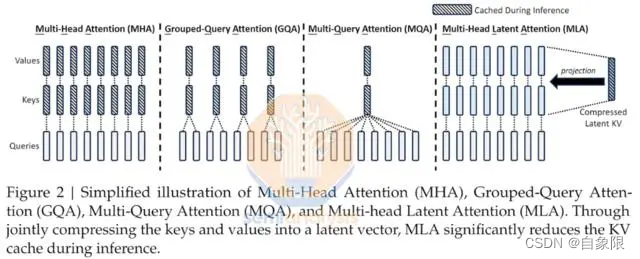
火山引擎“奇袭”阿里云
图片|电影《美国队长3》剧照 ©自象限原创 作者丨程心 编辑丨罗辑 大模型价格战,已经不是什么新闻。 从OpenAI发布GPT-4o,将API价格下调50%,并宣布面向普通用户免费开始,就标志着大模型的竞争从性能进入到了成本…...

牛客网刷题 | BC94 反向输出一个四位数
目前主要分为三个专栏,后续还会添加: 专栏如下: C语言刷题解析 C语言系列文章 我的成长经历 感谢阅读! 初来乍到,如有错误请指出,感谢! 描述 将一个四位数&…...

记一次MySQL执行修改语句超时问题
异常问题 原因分析 这个问题发生在开发环境,怀疑是提交事务时终止项目运行,没有提交该事务,造成死锁 调试该事务时时间太长,为什么说有这个原因呢,因为通过查找日志显示 The client was disconnected by the server …...
函数调用原理)
linux fork()函数调用原理
在Linux中,fork函数用于创建一个新的进程,该进程是调用进程的子进程。fork函数的实现涉及用户态和内核态之间的交互。下面我将详细说明fork函数在代码流程中的原理和用户态与内核态的交互过程。 用户态调用fork函数: 用户程序调用fork函数,该函数是libc库提供的一个封装函数…...

【电控笔记5.9】编码器脉冲计算速度MT法
总结 编码器的脉冲计算速度可以使用多种方法,其中一种常用的方法是“MT法” (Measuring Time Method),即测量时间法。该方法通过测量编码器脉冲间的时间来计算速度。这种方法在高精度速度测量中非常有效,特别是在速度较低时。 MT法计算速度的基本原理 MT法的基本原理是通过…...

go-zero 实战(4)
中间件 在 userapi 项目中引入中间件。go项目中的中间可以处理请求之前和之后的逻辑。 1. 在 userapi/internal目录先创建 middlewares目录,并创建 user.go文件 package middlewaresimport ("github.com/zeromicro/go-zero/core/logx""net/http&q…...

go语言泛型Generic最佳实践 --- slices包
在go的内置包slices中, 所有的函数函数都使用了泛型, 各种各样的泛型, 可以说这个包绝对是go语言泛型学习的最佳实践之一! 来,先来瞄一眼,看看这个slices包里面的函数原型定义: func BinarySe…...

【神经网络结构可视化】使用 Visualkeras 可视化 Keras / TensorFlow 神经网络结构
文章目录 Visualkeras介绍下载安装代码示例1、导入必要的库2、创建VGG16神经网络模型3、可视化神经网络结构4、完整代码5、使用教程 可视化自己创建的神经网络结构1、导入要的库2、创建自己的神经网络模型3、可视化神经网络结构图4、完整代码 Visualkeras介绍 Visualkeras是一…...

nvm安装nodejs/npm/nvm笔记
1 安装nvm, 指定路径nvm路径: D:\Program_Files\nvm\nvm指定路径nodejs 路径: D:\Program_Files\nvm\nodejs 2 进入nvm安装路径找到settings.xml文件,追加2行,设置镜像 node_mirror: https://npmmirror.com/mirrors/node/ npm_mirror: ht…...
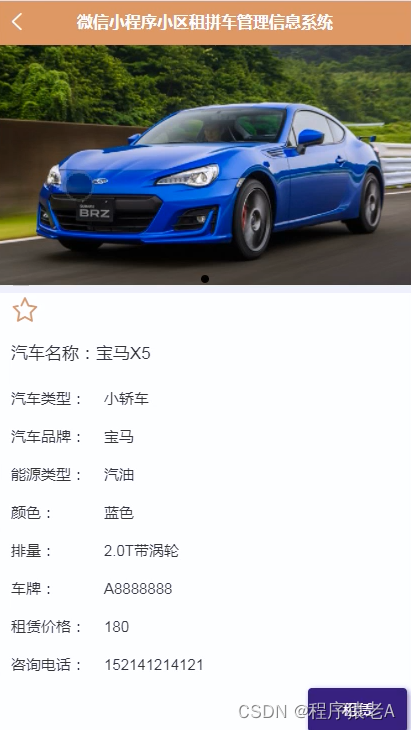
微信小程序源码-基于Java后端的小区租拼车管理信息系统毕业设计(附源码+演示录像+LW)
大家好!我是程序员一帆,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:微信小程序毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设…...
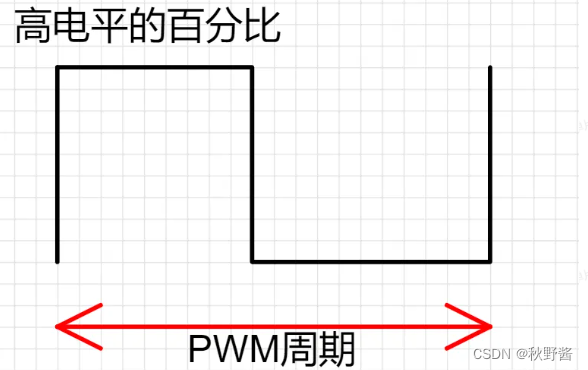
嵌入式进阶——LED呼吸灯(PWM)
🎬 秋野酱:《个人主页》 🔥 个人专栏:《Java专栏》《Python专栏》 ⛺️心若有所向往,何惧道阻且长 文章目录 PWM基础概念STC8H芯片PWMA应用PWM配置详解占空比 PWM基础概念 PWM全称是脉宽调制(Pulse Width Modulation)…...
一文读懂:http免费升级https
背景: 随着现在全民网络安全意识的日益提升,各个网站需要实现的https数量也随之提升,那么如何将原本网站的http访问方式升级为https呢? 该内容为如何免费将网站的http访问升级为https访问 论https的加密逻辑: 步骤 …...
)
算法刷题笔记 高精度除法(C++实现)
文章目录 题目描述求解思路实现代码 题目描述 给定两个非负整数(不含前导0)A,B,请你计算 A/B 的商和余数。 输入格式 共两行,第一行包含整数A,第二行包含整数B。 输出格式 共两行,第一行输…...

按月爬取天气数据可视化展示
从天气网分析,可以查询每个月的天气情况,这里按照url规则,传入年月,获取数据,最后进行可视化展示,最终效果: 下面是获取过程: 第一步: import requestsdef get_weather(month):url = f"https://lishi.tianqi.com/nanning/{month}.html"response = reques…...

VMware安装Ubuntu系统(超详细)
一.Ubuntu官网下载镜像 Ubuntu官网:Enterprise Open Source and Linux | Ubuntu 二.安装Ubuntu系统 选择文件->创建虚拟机新建虚拟机(ControlN),这里直接选择典型即可 选择稍后安装系统 选择linux Ubuntu 64位 填写虚拟机名称…...

数据清洗操作及众所周知【数据分析】
各位大佬好 ,这里是阿川的博客 , 祝您变得更强 个人主页:在线OJ的阿川 大佬的支持和鼓励,将是我成长路上最大的动力 阿川水平有限,如有错误,欢迎大佬指正 前面的博客 数据分析—技术栈和开发环境搭建 …...
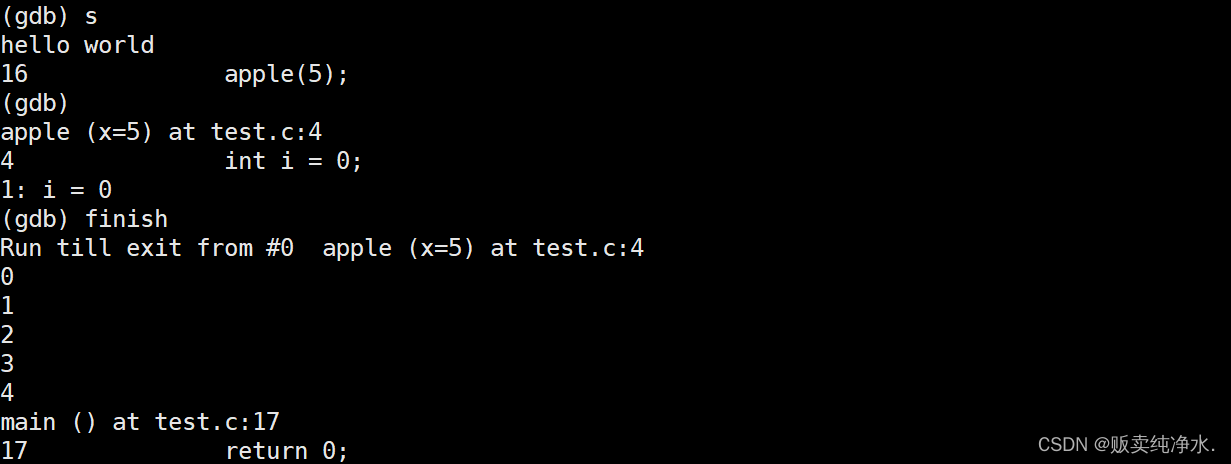
炫酷gdb
在VS里面调试很方便对吧?(F5直接调试,F10逐过程调试--不进函数,F11逐语句调试--进函数,F9创建断点),那在Linux中怎么调试呢? 我们需要用到一个工具:gdb 我们知道VS中程…...
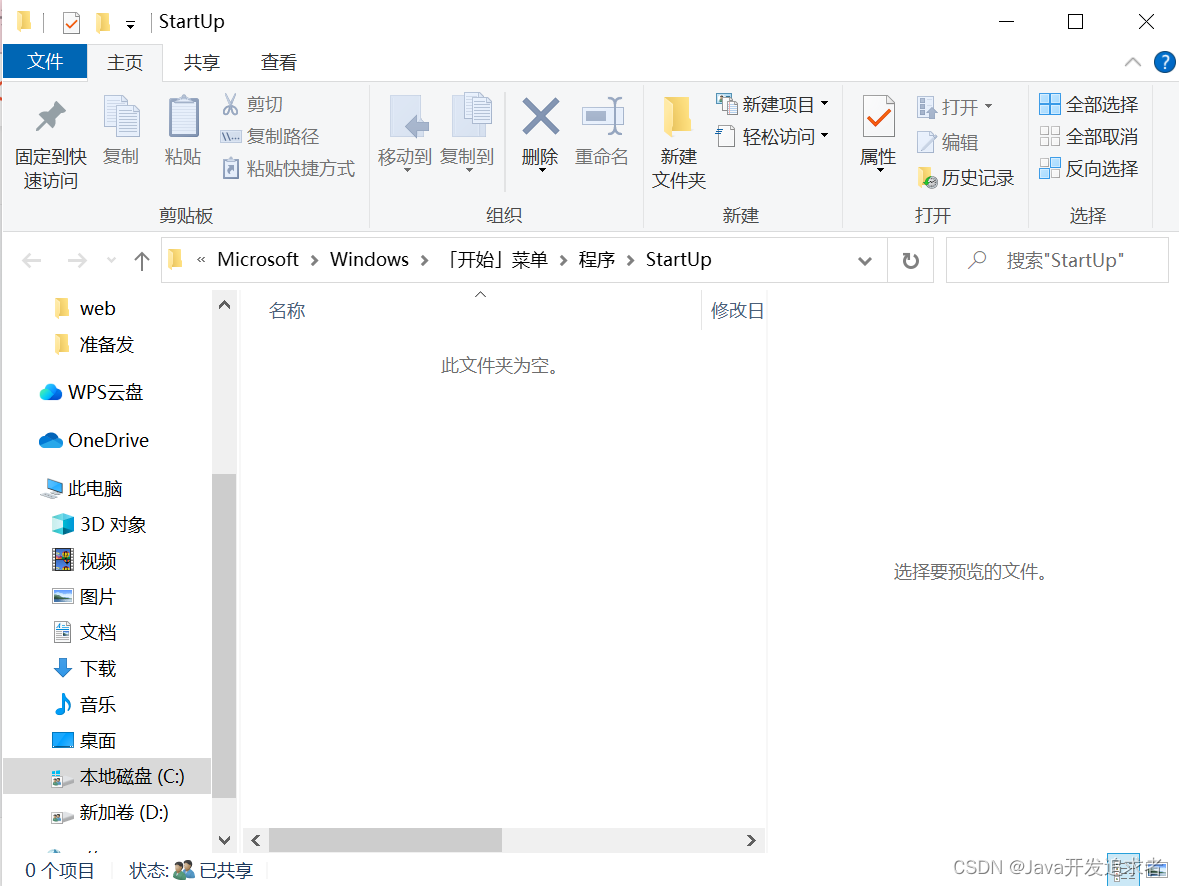
windows 7 10 11快捷键到启动页面
1.快速打开用户启动文件夹 shell:startup 方式2:快速打开系统启动文件夹 shell:Common Startup shell:Common Startup...

[处理器芯片]-6 超标量CPU实现之浮点运算
1 浮点运算单元FPU 超标量CPU中的浮点运算单元是专门处理浮点数运算的关键组件。浮点运算单元的设计涉及多个复杂的子模块和技术,以保证高效、准确地执行浮点数的加减法、乘法、除法、平方根等操作。 1)浮点数术语 浮点数通常采用IEEE 754标准表示&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
