[处理器芯片]-6 超标量CPU实现之浮点运算
1 浮点运算单元FPU
超标量CPU中的浮点运算单元是专门处理浮点数运算的关键组件。浮点运算单元的设计涉及多个复杂的子模块和技术,以保证高效、准确地执行浮点数的加减法、乘法、除法、平方根等操作。
1)浮点数术语
浮点数通常采用IEEE 754标准表示,包括三部分:符号位、指数位和尾数位。
半精度浮点数:16位,FP16,包括1位符号位,5位指数位,10位尾数位。
单精度浮点数:32位,FP32,包括1位符号位,8位指数位,23位尾数位。
双精度浮点数:64位,FP64,包括1位符号位,11位指数位,52位尾数位。
FP8 是一种新的浮点数格式,主要用于机器学习加速器和一些低精度计算场景,两种变种:
E4M3(Exponent 4 bits, Mantissa 3 bits):包括1位符号位,4位指数位,3位尾数位。
E5M2(Exponent 5 bits, Mantissa 2 bits):包括1位符号位,5位指数位,2位尾数位。
BF16 (16位浮点数,Brain Floating Point, BP16),是一种为机器学习优化的16位浮点数格式,保留了单精度浮点数的指数范围,但减少了尾数的位数:包括1位符号位,8位指数位,7位尾数位。BF16 具有与单精度浮点数(FP32)相同的指数范围,因此可以表示同样大的数值范围,但精度较低,这使得 BF16 特别适合于训练深度神经网络,因为它可以减少内存带宽和存储需求,同时保持足够的数值范围。
2)浮点运算单元组成
加法器和减法器,乘法器,除法器,平方根计算单元,归约和规范化单元,异常处理单元
3)浮点加法和减法单元
浮点加减法需要处理对齐、加减运算和归约等步骤:
1)对齐:比较指数(对齐操作数,使其指数相同)、移位尾数(根据指数差调整尾数)。
2)加法/减法:计算尾数(执行加法或减法运算)
3)规范化结果:归约结果(规范化结果,使最高有效位位于合适位置)、舍入结果(根据IEEE 754标准,对结果进行舍入操作:向偶数舍入、向零舍入、向正无穷舍入、向负无穷舍入)。
逻辑实现
module FPAdder (
input [31:0] a, b, // 两个单精度浮点数
output [31:0] result
);
// 提取符号位、指数位和尾数位
wire sign_a = a[31];
wire [7:0] exp_a = a[30:23];
wire [23:0] frac_a = {1'b1, a[22:0]};
wire sign_b = b[31];
wire [7:0] exp_b = b[30:23];
wire [23:0] frac_b = {1'b1, b[22:0]};
// 对齐指数和尾数
wire [7:0] exp_diff = exp_a - exp_b;
wire [23:0] aligned_frac_b = frac_b >> exp_diff;
// 执行加法
wire [24:0] frac_sum = frac_a + aligned_frac_b;
// 规范化结果
wire [7:0] result_exp = exp_a + 1;
wire [23:0] result_frac = frac_sum[24] ? frac_sum[23:0] : frac_sum[22:0];
assign result = {sign_a, result_exp, result_frac[22:0]};
endmodule
4)浮点乘法单元
浮点乘法包括指数相加和尾数相乘两个主要步骤:
1)指数相加:结果指数是两个操作数指数之和,减去一个偏置值。
2)尾数相乘:乘法操作需要高效的部分积生成和压缩机制。
3)规范化结果。
逻辑实现
module FPMultiplier (
input [31:0] a, b, // 两个单精度浮点数
output [31:0] result
);
// 提取符号位、指数位和尾数位
wire sign_a = a[31];
wire [7:0] exp_a = a[30:23];
wire [23:0] frac_a = {1'b1, a[22:0]};
wire sign_b = b[31];
wire [7:0] exp_b = b[30:23];
wire [23:0] frac_b = {1'b1, b[22:0]};
// 计算符号
wire result_sign = sign_a ^ sign_b;
// 计算指数
wire [8:0] result_exp = exp_a + exp_b - 8'd127;
// 尾数相乘
wire [47:0] frac_mult = frac_a * frac_b;
// 规范化结果
wire [23:0] result_frac = frac_mult[47] ? frac_mult[46:24] : frac_mult[45:23];
wire [7:0] final_exp = frac_mult[47] ? result_exp + 1 : result_exp;
assign result = {result_sign, final_exp[7:0], result_frac[22:0]};
endmodule
5)浮点除法和平方根单元
浮点除法和平方根计算通常比加减法和乘法更复杂,可以采用多种算法实现,如牛顿-拉弗森法、非恢复性除法等。
浮点除法主要步骤如下:
符号计算:结果的符号是被除数和除数符号的异或。
指数相减:结果的指数是被除数指数减去除数指数再加上偏置值。
尾数除法:计算尾数的商。
规范化结果。
逻辑实现
module FPDivider(
input [31:0] a, b, // 两个单精度浮点数
output [31:0] result
);
// 提取符号位、指数位和尾数位
wire sign_a = a[31];
wire [7:0] exp_a = a[30:23];
wire [23:0] frac_a = {1'b1, a[22:0]}; // 隐含1
wire sign_b = b[31];
wire [7:0] exp_b = b[30:23];
wire [23:0] frac_b = {1'b1, b[22:0]}; // 隐含1
// 计算符号
wire result_sign = sign_a ^ sign_b;
// 计算指数
wire [8:0] result_exp = exp_a - exp_b + 8'd127;
// 尾数相除
wire [47:0] frac_div = (frac_a << 23) / frac_b;
// 规范化结果
wire [23:0] result_frac = frac_div[46] ? frac_div[46:24] : frac_div[45:23];
wire [7:0] final_exp = frac_div[46] ? result_exp + 1 : result_exp;
assign result = {result_sign, final_exp[7:0], result_frac[22:0]};
Endmodule
浮点开方主要步骤如下:
符号计算:平方根运算结果的符号为正。
指数计算:结果的指数是操作数指数的一半再加上偏置值。
尾数计算:计算尾数的平方根。
规范化结果。
逻辑实现
module FPSqrt(
input [31:0] a,
output [31:0] result
);
wire [7:0] exp_a;
wire [23:0] frac_a;
wire [7:0] result_exp;
wire [23:0] frac_result;
wire [23:0] norm_frac_result;
wire [7:0] norm_exp_result;
// 各个阶段模块化实现
FPSqrt_Preprocess preprocess (.a(a), .exp_a(exp_a), .frac_a(frac_a));
FPSqrt_Exponent exponent (.exp_a(exp_a), .result_exp(result_exp));
FPSqrt_Mantissa mantissa (.frac_a(frac_a), .frac_result(frac_result));
FPSqrt_Normalize normalize (.frac_result(frac_result), .result_exp(result_exp),
.norm_frac_result(norm_frac_result), .norm_exp_result(norm_exp_result));
FPSqrt_Round round (.norm_frac_result(norm_frac_result), .norm_exp_result(norm_exp_result),
.final_result(result));
endmodule
6)归约和规范化单元
归约和规范化用于确保结果符合标准的浮点数格式,包括对结果的尾数进行移位处理,以使结果尾数的最高有效位为1,并调整指数值。
7)异常处理单元
异常处理包括对各种浮点运算异常的检测和处理,例如:
溢出:结果超出可表示的范围。
下溢:结果小于可表示的最小值。
除零:除法操作中分母为零。
无效操作:如0/0或sqrt(-1)。
2 单指令多数据SIMD
SIMD(Single Instruction, Multiple Data)是一种并行计算架构,通过扩展处理器的指令集来操作多个数据元素,这些数据元素通常被存储在一个大的寄存器中,例如处理器可以使用一条指令同时对四个 32 位浮点数或八个 16 位整数进行运算。SIMD设计在现代超标量CPU中被广泛应用,特别是在多媒体处理、科学计算和其他需要处理大量数据的应用中。
1)常见的 SIMD 指令集
Intel MMX、SSE、AVX 和 AVX-512
ARM NEON
IBM AltiVec
AMD 3DNow!
2)SIMD 寄存器
SIMD 指令通常使用宽寄存器来存储多个数据元素。
MMX 寄存器:64 位宽,通常处理 8 个 8 位数据或 4 个 16 位数据。
SSE 寄存器:128 位宽,通常处理 4 个 32 位浮点数或 16 个 8 位整数。
AVX 寄存器:256 位宽,通常处理 8 个 32 位浮点数或 32 个 8 位整数。
AVX-512 寄存器:512 位宽,处理的数据量更大。
3)SIMD操作数
SIMD 指令的操作数通常表示为向量类型的数据。例如在 Intel 的 AVX 指令集中,ymm 寄存器表示 256 位寄存器,其中可以存储 8 个 32 位浮点数。
4)SIMD 指令操作
算术运算:加法、减法、乘法、除法等
逻辑运算:与、或、非、异或等
移位运算:左移、右移、算术右移等
比较运算:大于、小于、等于等
数据搬移:加载、存储、混合、打包和解包数据
5)SIMD执行步骤
指令获取和解码:处理器从内存中获取 SIMD 指令,并将其解码为内部操作码和操作数。
数据加载:将操作数从内存加载到 SIMD 寄存器中。
并行计算:在多个数据元素上并行执行指令。
结果存储:将计算结果从 SIMD 寄存器存储回内存或其他寄存器中。
SIMD 加法器示例(并行处理四个 32 位整数)
module SIMDAdder (
input [127:0] A, // 四个 32 位整数输入 A
input [127:0] B, // 四个 32 位整数输入 B
output [127:0] Sum // 四个 32 位整数输出 Sum
);
assign Sum[31:0] = A[31:0] + B[31:0]; // 第一个整数加法
assign Sum[63:32] = A[63:32] + B[63:32]; // 第二个整数加法
assign Sum[95:64] = A[95:64] + B[95:64]; // 第三个整数加法
assign Sum[127:96] = A[127:96] + B[127:96]; // 第四个整数加法
endmodule
6)SIMD 优化技术
数据对齐:确保数据在内存中的对齐,以便于 SIMD 加载和存储操作。
数据预取:提前加载数据以减少等待时间,提高指令执行效率。
向量化:将标量代码转换为向量代码,使其能够利用 SIMD 指令集。
循环展开:减少循环控制开销,通过展开循环体使更多操作在同一条指令中执行。
指令调度:优化指令顺序,以最大限度地减少依赖关系和等待时间。
7)SIMD 的应用
多媒体处理:图像处理、音频处理、视频编码和解码。
科学计算:矩阵运算、向量运算、快速傅里叶变换(FFT)。
数据分析:大数据处理、机器学习、神经网络。
加密和解密:数据加密标准(AES)、安全哈希算法(SHA)。
相关文章:

[处理器芯片]-6 超标量CPU实现之浮点运算
1 浮点运算单元FPU 超标量CPU中的浮点运算单元是专门处理浮点数运算的关键组件。浮点运算单元的设计涉及多个复杂的子模块和技术,以保证高效、准确地执行浮点数的加减法、乘法、除法、平方根等操作。 1)浮点数术语 浮点数通常采用IEEE 754标准表示&…...
又有人叫嚣:AI取代前端,来给你几张图,看能不能憋死AI。
总有自媒体人,为了些许流量,在大放厥词,说截个图给AI,AI就能输出前端代码,这是啥都敢说,吹牛不上税。 我来给你几张贝格前端工场日常接的大数据项目相关的图,你让AI生成代码,取代前…...

ISCC2024个人挑战赛WP-WEB
(非官方解,以下内容均互联网收集的信息和个人思路,仅供学习参考) 还没想好名字的塔防游戏 GET /world.js HTTP/1.1 Host: 101.200.138.180:17345 Accept: text/html,application/xhtmlxml,application/xml;q0.9,image/avif,i…...
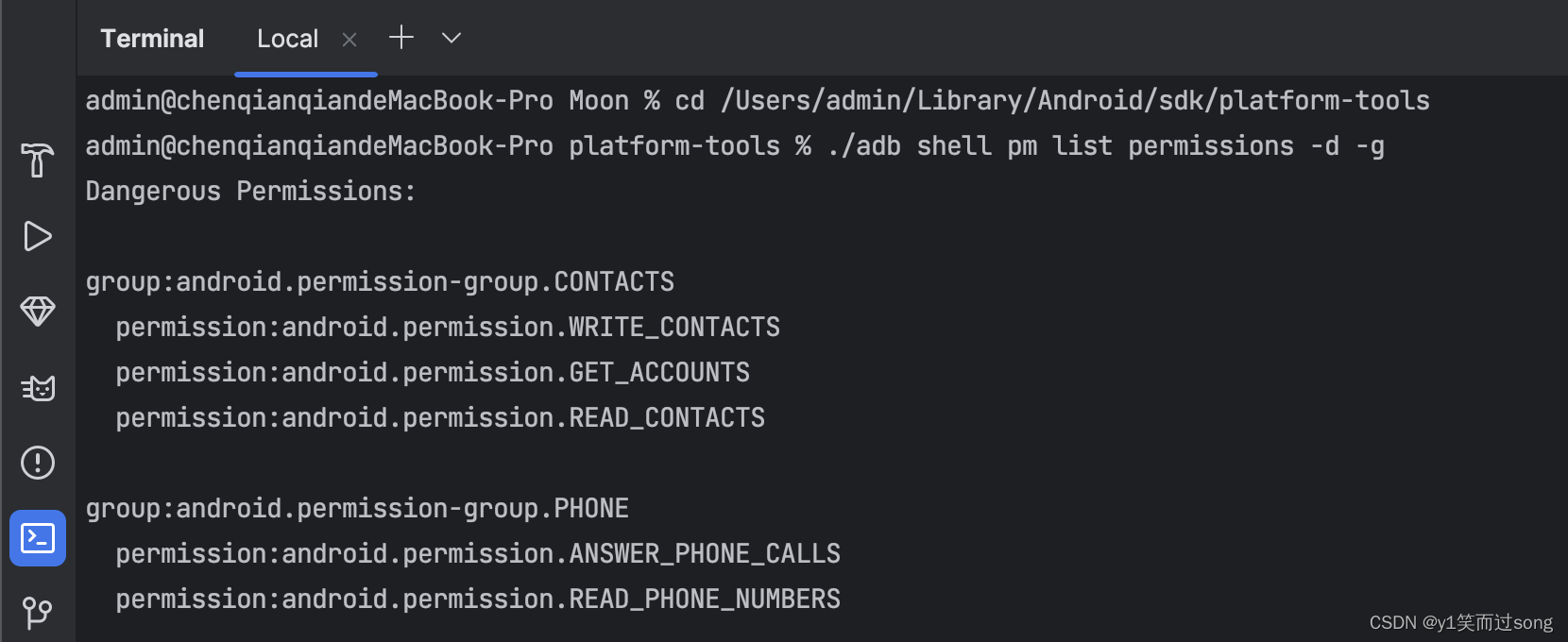
Android 使用 adb 列出设备上所有危险权限
步骤1:确定 Android SDK 位置 打开 Android Studio 的设置,并来到 Languages & Frameworks › Android SDK 处: 这里可以看到 Android SDK 目录的位置: 例如:/Users/admin/Library/Android/sdk。 复制这个路径&am…...

Spring AOP源码分析
#### AOP(面向切面编程)作用及其优势 作用:在程序运行期间,在不修改源码的情况下对方法进行功能增强(通知) 优势:减少重复代码,提高代码复用性,提高代码可维护性…...
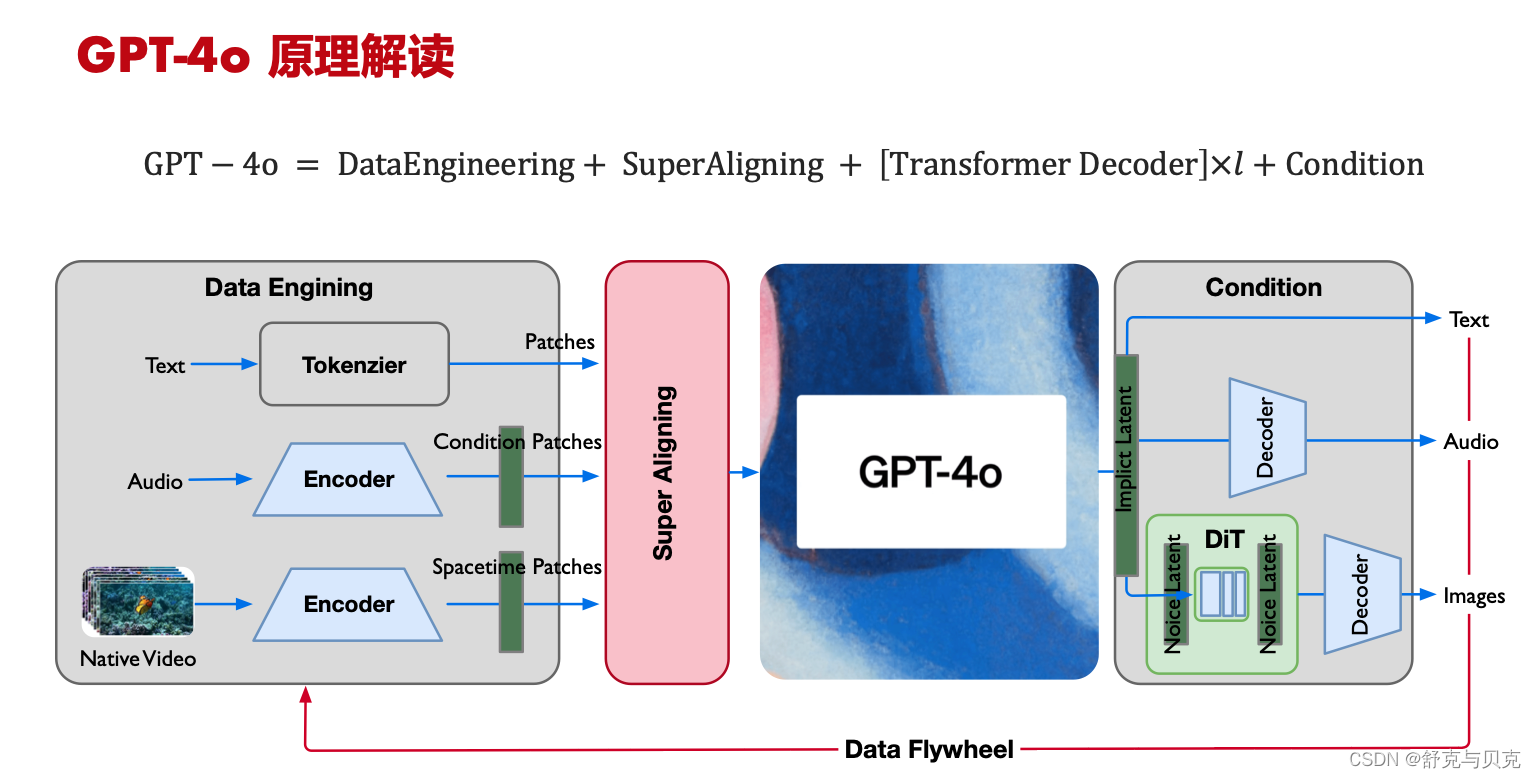
[LLM]从GPT-4o原理到下一代人机交互技术
一 定义 GPT-4o作为OpenAI推出的一款多模态大型语言模型,代表了这一交互技术的重要发展方向。 GPT-4o是OpenAI推出的最新旗舰级人工智能模型,它是GPT系列的一个重要升级,其中的"o"代表"Omni",中文意思是“全…...
)
【Spring】AOP——通知(Advice)
1、通知(Advice) 1.1简介 在AOP中,通知(Advice)是切面(Aspect)中的一部分,用于定义在连接点(Joinpoint)处应该执行的操作。通知类型可以在AOP框架中配置和使…...

python中的一些基础概念
在python中整型数据可以和浮点型数据相加,在python中字符串数据可以进行相加, 在python中整型数据可以和布尔类型进行算术运算。此时True当做1,False当做0但是这样的操作是没有意义的, python中只有字符串类型没有字符类型&…...

8.Redis之hash类型
1.hash类型的基本介绍 哈希表[之前学过的所有数据结构中,最最重要的] 1.日常开发中,出场频率非常高. 2.面试中,非常重要的考点, Redis 自身已经是键值对结构了Redis 自身的键值对就是通过 哈希 的方式来组织的 把 key 这一层组织完成之后, 到了 value 这一层~~ value 的其中…...

Edge浏览器
微软 Edge 是由微软开发的网络浏览器,它是 Windows 10 操作系统的默认浏览器,取代了之前的 Internet Explorer。Edge 浏览器在设计上注重性能、安全性和易用性,同时也提供了许多实用的功能,如内置笔记、阅读视图、集成的语音助手等…...

springboot项目中图片上传之后需要重启工程才能看到图片?
需求背景 最近在做一个用户自定义上传头像的小需求,用户上传头像然后需要立马回显。 需求是很常见的、正当的需求。如果不使用到对象存储这类服务,我们把用户头像的图片文件仅存在本地就可以了。我们在开发的过程中为了工程管理方便通常下意识会将图片…...

打卡信奥刷题(20)用Scratch图形化工具信奥B3756 [信息与未来 2021] 幸运数字
本题的基础是进制转换,关于2进制转换可以参考打卡信奥刷题(19)用Scratch图形化工具信奥B3972 [语言月赛 202405] 二进制 题解 知道了2进制,来实现5进制、7进制、9进制是一样的。 [信息与未来 2021] 幸运数字 题目描述 如果⼀个…...
Stream流模式通信及示例
Stream流模式通信是指在计算机网络中,数据作为连续的字节流传输而不是独立的数据包。它是一种面向连接的通信方式,常见于TCP(传输控制协议)。以下是Stream流模式通信的基本概念和一个简单的示例。 基本概念 面向连接࿱…...
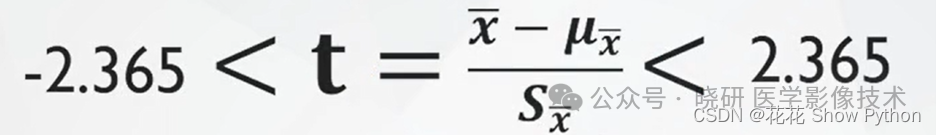
从0开始学统计-t分布
1.t分布是如何被发现的? t分布最早由英国统计学家威廉塞弗顿(William Sealy Gosset)在1908年提出。塞弗顿是爱尔兰的一名酿酒厂的统计学家,他的工作需要对小样本数据进行分析。由于当时样本量较小(通常小于30…...

Git总结超全版
最近想系统的回顾一下Git的使用,如果只想快速的集成git到idea,可以参考另一篇我的博客中的git部分 目录 版本管理工具简介Git安装与配置Git远程仓库配置 Git常用命令为常用命令配置别名(可选)Git忽略文件.gitignore一些概念*本地仓库操作删除仓库内容 *远…...
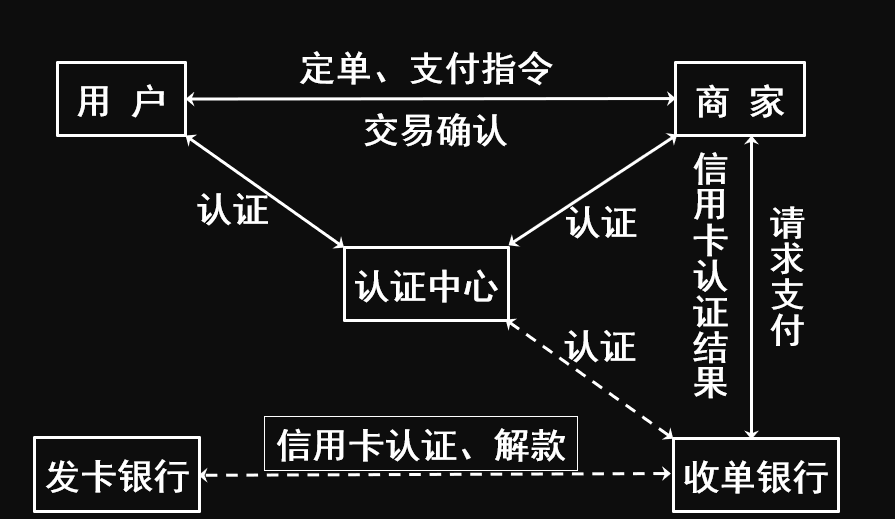
网络安全之安全协议浅谈
安全协议 安全协议概述安全协议分类IPSecIPSec安全协议IPSec架构IPSec封装模式AH协议ESP协议SET协议SET协议电子交易模型SET协议安全目标认证中心CA 安全协议概述 安全协议是信息交换安全的核心,它在网络不同层次上、针对不同应用,通过对各种密码学技术…...

华为云部署前端项目发生的事
今天刚买了一个云服务,想着部署一下前端项目: 使用的是 docker nginx 部署 部署方法,在以往的文章中有介绍,如有兴趣可以看看docker 部署; 结果发现部署成功之后,竟然无法访问,从命令来看&…...

需求:实现一个可以统计代码的运行时间
需求:有一个做加法计算的函数,要统计执行这个加法函数代码运行了多久 import timedef add(a, b):time.sleep(1)return a bst time.time() add(100, 200) et time.time() print("该函数运行时间为:", et - st) 学了闭包&#x…...

软考高级之redis中使用zset实现延迟队列,你答对了么?
实现延迟队列的思路 zset的特性,带有分数的排序,以时间戳作为分数进行排序 添加任务 zdd取出任务 zrangbyscore执行任务 zrem 定时任务 public static void main(String[] args) {Jedis jedis new Jedis("ip", 6379);TimerTask task new …...

CS 下载安装详解
目录 CS简介: CS下载地址: CS的安装: CS简介: CS为目前渗透中常用的一款工具,它的强大在于控制windows木马,CS主要控制windows木马。 CS下载地址: 链接:https://pan.baidu.com/…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
