当前位置： 首页 > news >正文

按月爬取天气数据可视化展示

news 2026/2/11 5:07:57

从天气网分析，可以查询每个月的天气情况，这里按照url规则，传入年月，获取数据，最后进行可视化展示，最终效果：

下面是获取过程：

第一步： 

import requestsdef get_weather(month):url = f"https://lishi.tianqi.com/nanning/{month}.html"response = requests.get(url)data = response.textprint(data)return dataget_weather("202307")

提示如下： 

PS D:\soft\src\python-src\python05-icecream> & D:/soft/python/Python38/python.exe d:/soft/src/python-src/python05-icecream/weather.py
🍦 data: ('<!DOCTYPE HTML PUBLIC "-//IETF//DTD HTML 2.0//EN"><html><head><title>403 '"Forbidden</title></head><body><h1>403 Forbidden&l

相关文章：

按月爬取天气数据可视化展示

从天气网分析，可以查询每个月的天气情况，这里按照url规则，传入年月，获取数据，最后进行可视化展示，最终效果： 下面是获取过程： 第一步： import requestsdef get_weather(month):url = f"https://lishi.tianqi.com/nanning/{month}.html"response = reques…...

编程日记 2024/5/26 17:40:39

VMware安装Ubuntu系统(超详细)

一.Ubuntu官网下载镜像 Ubuntu官网&#xff1a;Enterprise Open Source and Linux | Ubuntu 二.安装Ubuntu系统 选择文件->创建虚拟机新建虚拟机&#xff08;ControlN&#xff09;&#xff0c;这里直接选择典型即可 选择稍后安装系统 选择linux Ubuntu 64位 填写虚拟机名称…...

编程日记 2024/5/26 17:39:38

数据清洗操作及众所周知【数据分析】

各位大佬好 &#xff0c;这里是阿川的博客 &#xff0c; 祝您变得更强 个人主页&#xff1a;在线OJ的阿川 大佬的支持和鼓励&#xff0c;将是我成长路上最大的动力 阿川水平有限&#xff0c;如有错误&#xff0c;欢迎大佬指正 前面的博客 数据分析—技术栈和开发环境搭建 …...

编程日记 2024/5/26 17:37:37

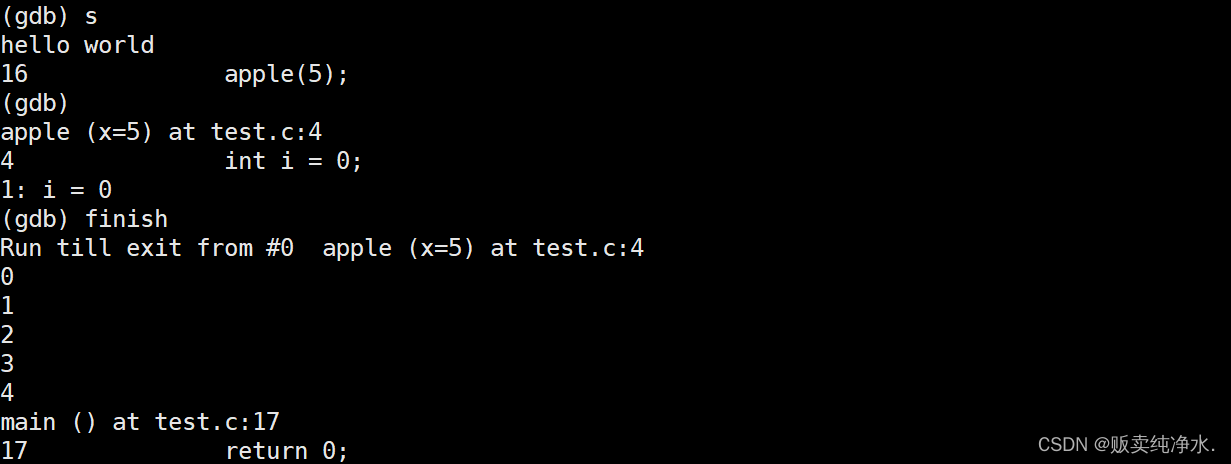
炫酷gdb

在VS里面调试很方便对吧&#xff1f;&#xff08;F5直接调试&#xff0c;F10逐过程调试--不进函数&#xff0c;F11逐语句调试--进函数&#xff0c;F9创建断点&#xff09;&#xff0c;那在Linux中怎么调试呢&#xff1f; 我们需要用到一个工具&#xff1a;gdb 我们知道VS中程…...

编程日记 2024/5/26 17:35:35

windows 7 10 11快捷键到启动页面

1.快速打开用户启动文件夹 shell:startup 方式2&#xff1a;快速打开系统启动文件夹 shell:Common Startup shell:Common Startup...

编程日记 2024/5/26 17:34:34

[处理器芯片]-6 超标量CPU实现之浮点运算

1 浮点运算单元FPU 超标量CPU中的浮点运算单元是专门处理浮点数运算的关键组件。浮点运算单元的设计涉及多个复杂的子模块和技术&#xff0c;以保证高效、准确地执行浮点数的加减法、乘法、除法、平方根等操作。 1&#xff09;浮点数术语 浮点数通常采用IEEE 754标准表示&…...

编程日记 2024/5/26 17:33:33

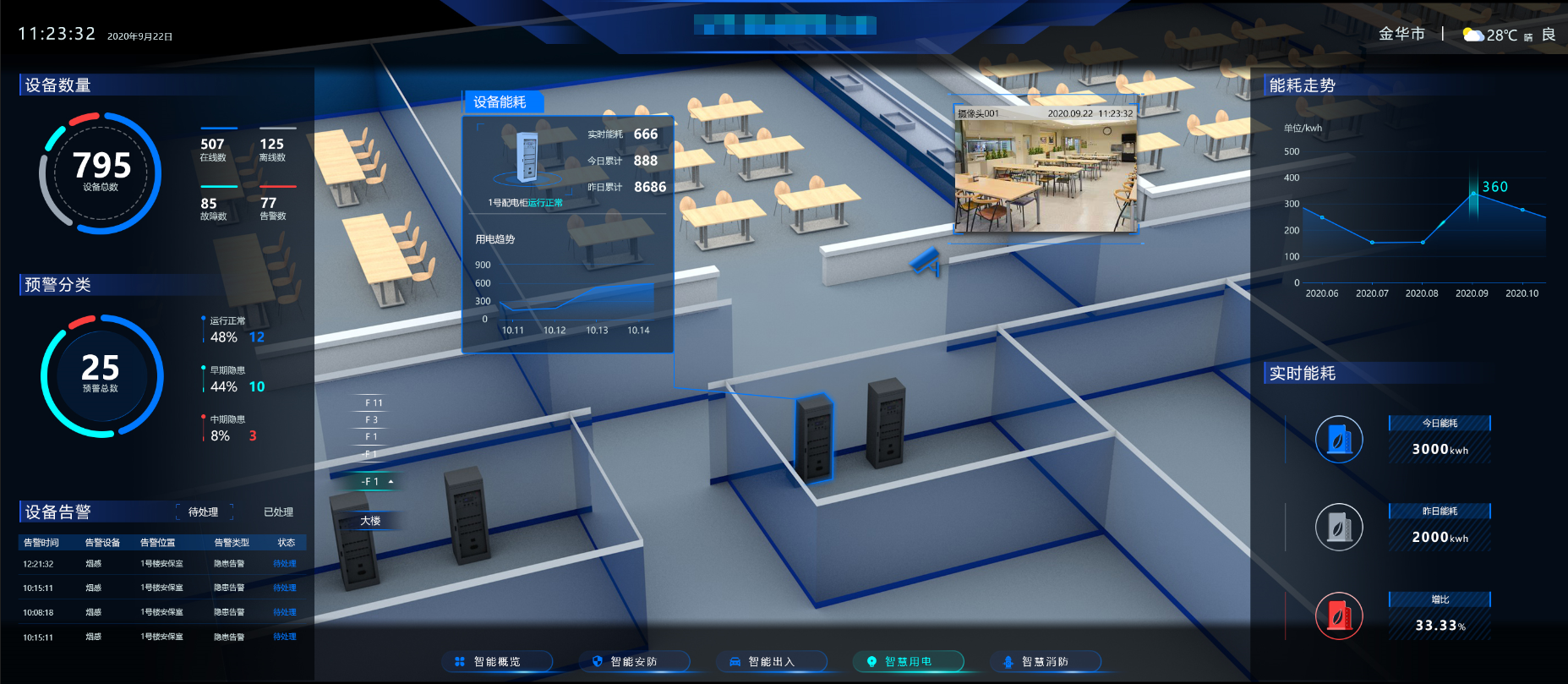
又有人叫嚣：AI取代前端，来给你几张图，看能不能憋死AI。

总有自媒体人&#xff0c;为了些许流量&#xff0c;在大放厥词&#xff0c;说截个图给AI&#xff0c;AI就能输出前端代码&#xff0c;这是啥都敢说&#xff0c;吹牛不上税。 我来给你几张贝格前端工场日常接的大数据项目相关的图&#xff0c;你让AI生成代码&#xff0c;取代前…...

编程日记 2024/5/26 17:32:32

ISCC2024个人挑战赛WP-WEB

&#xff08;非官方解&#xff0c;以下内容均互联网收集的信息和个人思路&#xff0c;仅供学习参考&#xff09; 还没想好名字的塔防游戏 GET /world.js HTTP/1.1 Host: 101.200.138.180:17345 Accept: text/html,application/xhtmlxml,application/xml;q0.9,image/avif,i…...

编程日记 2024/5/26 17:31:31

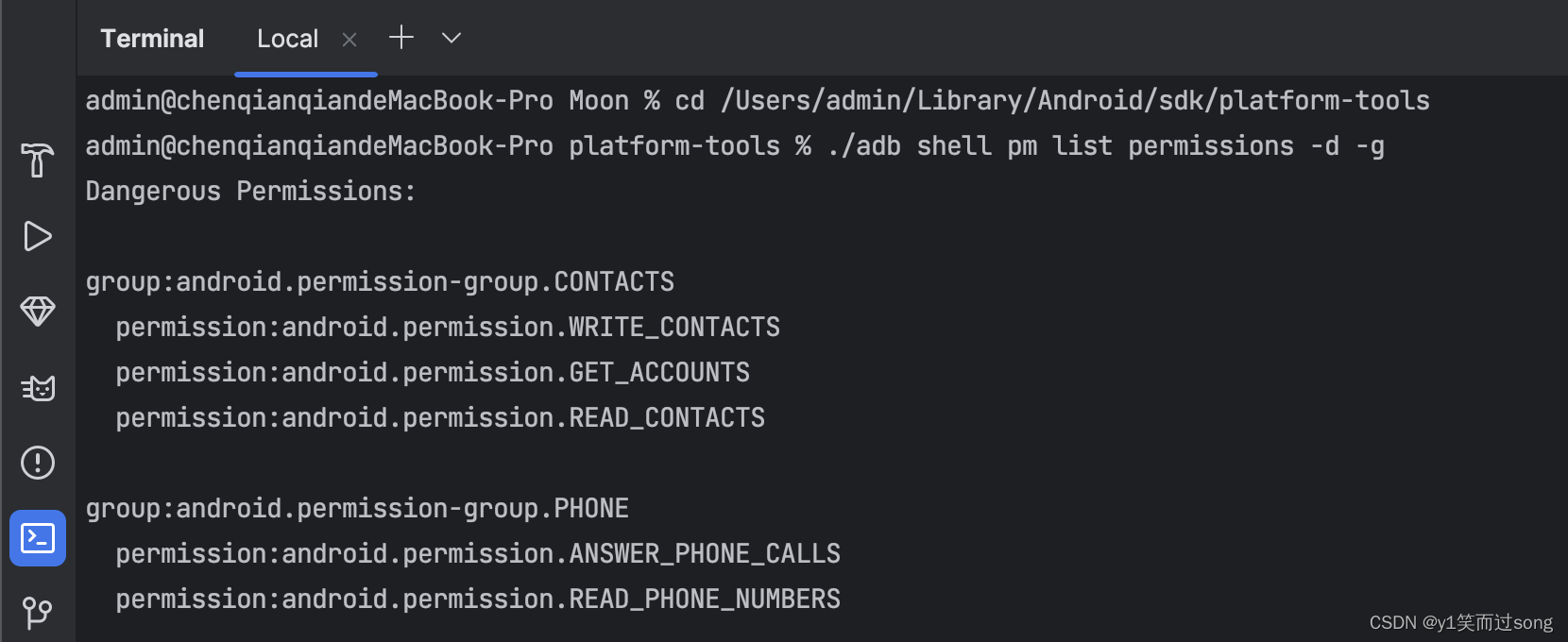
Android 使用 adb 列出设备上所有危险权限

步骤1&#xff1a;确定 Android SDK 位置 打开 Android Studio 的设置&#xff0c;并来到 Languages & Frameworks › Android SDK 处&#xff1a; 这里可以看到 Android SDK 目录的位置&#xff1a; 例如&#xff1a;/Users/admin/Library/Android/sdk。 复制这个路径&am…...

编程日记 2024/5/26 17:30:30

Spring AOP源码分析

#### AOP&#xff08;面向切面编程&#xff09;作用及其优势 作用&#xff1a;在程序运行期间&#xff0c;在不修改源码的情况下对方法进行功能增强&#xff08;通知&#xff09; 优势&#xff1a;减少重复代码&#xff0c;提高代码复用性&#xff0c;提高代码可维护性&#xf…...

编程日记 2024/5/26 17:28:28

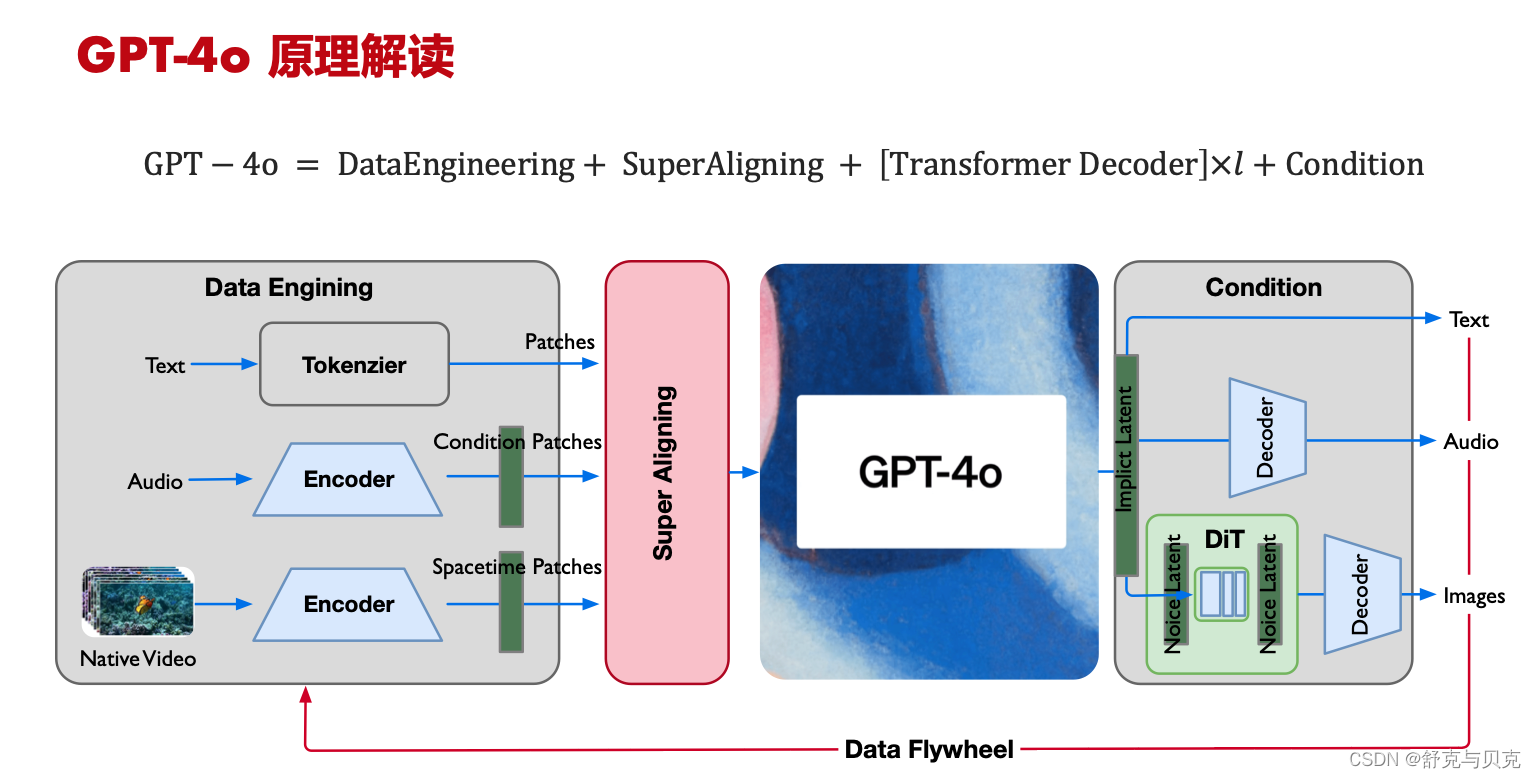
[LLM]从GPT-4o原理到下一代人机交互技术

一 定义 GPT-4o作为OpenAI推出的一款多模态大型语言模型&#xff0c;代表了这一交互技术的重要发展方向。 GPT-4o是OpenAI推出的最新旗舰级人工智能模型&#xff0c;它是GPT系列的一个重要升级&#xff0c;其中的"o"代表"Omni"&#xff0c;中文意思是“全…...

编程日记 2024/5/26 17:25:25

【Spring】AOP——通知（Advice）

1、通知&#xff08;Advice&#xff09; 1.1简介 在AOP中&#xff0c;通知&#xff08;Advice&#xff09;是切面&#xff08;Aspect&#xff09;中的一部分&#xff0c;用于定义在连接点&#xff08;Joinpoint&#xff09;处应该执行的操作。通知类型可以在AOP框架中配置和使…...

编程日记 2024/5/26 17:24:23

python中的一些基础概念

在python中整型数据可以和浮点型数据相加&#xff0c;在python中字符串数据可以进行相加&#xff0c; 在python中整型数据可以和布尔类型进行算术运算。此时True当做1&#xff0c;False当做0但是这样的操作是没有意义的&#xff0c; python中只有字符串类型没有字符类型&…...

编程日记 2024/5/26 17:20:18

8.Redis之hash类型

1.hash类型的基本介绍 哈希表[之前学过的所有数据结构中,最最重要的] 1.日常开发中,出场频率非常高. 2.面试中,非常重要的考点, Redis 自身已经是键值对结构了Redis 自身的键值对就是通过 哈希 的方式来组织的 把 key 这一层组织完成之后, 到了 value 这一层~~ value 的其中…...

编程日记 2024/5/26 17:19:17

Edge浏览器

微软 Edge 是由微软开发的网络浏览器&#xff0c;它是 Windows 10 操作系统的默认浏览器&#xff0c;取代了之前的 Internet Explorer。Edge 浏览器在设计上注重性能、安全性和易用性&#xff0c;同时也提供了许多实用的功能&#xff0c;如内置笔记、阅读视图、集成的语音助手等…...

编程日记 2024/5/26 17:17:15

springboot项目中图片上传之后需要重启工程才能看到图片？

需求背景 最近在做一个用户自定义上传头像的小需求&#xff0c;用户上传头像然后需要立马回显。 需求是很常见的、正当的需求。如果不使用到对象存储这类服务&#xff0c;我们把用户头像的图片文件仅存在本地就可以了。我们在开发的过程中为了工程管理方便通常下意识会将图片…...

编程日记 2024/5/26 17:15:13

打卡信奥刷题（20）用Scratch图形化工具信奥B3756 [信息与未来 2021] 幸运数字

本题的基础是进制转换&#xff0c;关于2进制转换可以参考打卡信奥刷题&#xff08;19&#xff09;用Scratch图形化工具信奥B3972 [语言月赛 202405] 二进制 题解 知道了2进制&#xff0c;来实现5进制、7进制、9进制是一样的。 [信息与未来 2021] 幸运数字 题目描述 如果⼀个…...

编程日记 2024/5/26 17:14:12

Stream流模式通信及示例

Stream流模式通信是指在计算机网络中&#xff0c;数据作为连续的字节流传输而不是独立的数据包。它是一种面向连接的通信方式&#xff0c;常见于TCP&#xff08;传输控制协议&#xff09;。以下是Stream流模式通信的基本概念和一个简单的示例。 基本概念 面向连接&#xff1…...

编程日记 2024/5/26 17:11:09

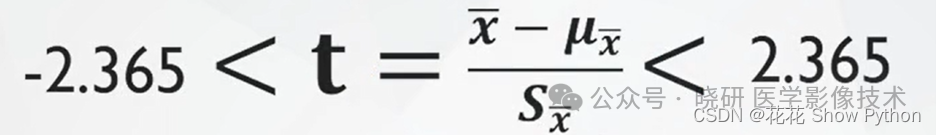
从0开始学统计-t分布

1.t分布是如何被发现的&#xff1f; t分布最早由英国统计学家威廉塞弗顿&#xff08;William Sealy Gosset&#xff09;在1908年提出。塞弗顿是爱尔兰的一名酿酒厂的统计学家&#xff0c;他的工作需要对小样本数据进行分析。由于当时样本量较小&#xff08;通常小于30&#xf…...

编程日记 2024/5/26 17:10:07

Git总结超全版

最近想系统的回顾一下Git的使用&#xff0c;如果只想快速的集成git到idea&#xff0c;可以参考另一篇我的博客中的git部分 目录 版本管理工具简介Git安装与配置Git远程仓库配置 Git常用命令为常用命令配置别名(可选)Git忽略文件.gitignore一些概念*本地仓库操作删除仓库内容 *远…...

编程日记 2024/5/26 17:08:05

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度​

一、引言&#xff1a;多云环境的技术复杂性本质​​ 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时&#xff0c;​​基础设施的技术债呈现指数级积累​​。网络连接、身份认证、成本管理这三大核心挑战相互嵌套&#xff1a;跨云网络构建数据…...

编程新知 2026/2/11 0:21:49

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/10/5 2:30:38

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

深入剖析AI大模型：大模型时代的 Prompt 工程全解析

今天聊的内容&#xff0c;我认为是AI开发里面非常重要的内容。它在AI开发里无处不在&#xff0c;当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗"&#xff0c;或者让翻译模型 "将这段合同翻译成商务日语" 时&#xff0c;输入的这句话就是 Prompt。…...

编程新知 2026/2/8 20:42:53

django filter 统计数量 按属性去重

在Django中&#xff0c;如果你想要根据某个属性对查询集进行去重并统计数量&#xff0c;你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求&#xff1a; 方法1&#xff1a;使用annotate()和Count 假设你有一个模型Item&#xff0c;并且你想…...

编程新知 2026/1/11 2:37:51

将对透视变换后的图像使用Otsu进行阈值化，来分离黑色和白色像素。这句话中的Otsu是什么意思？

Otsu 是一种自动阈值化方法&#xff0c;用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理&#xff0c;能够自动确定一个阈值&#xff0c;将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

编程新知 2026/1/9 19:36:58

《通信之道——从微积分到 5G》读书总结

第1章 绪 论 1.1 这是一本什么样的书 通信技术&#xff0c;说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号&#xff08;调制&#xff09; 把信息从信号中抽取出来&am…...

编程新知 2026/2/7 11:01:56

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2026/2/4 23:47:47

前端开发面试题总结-JavaScript篇(一)

文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包&#xff08;Closure&#xff09;&#xff1f;闭包有什么应用场景和潜在问题&#xff1f;2.解释 JavaScript 的作用域链&#xff08;Scope Chain&#xff09; 二、原型与继承3.原型链是什么&#xff1f;如何实现继承&a…...

编程新知 2026/2/1 3:12:03

Mysql中select查询语句的执行过程

目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析&#xff08;Parser&#xff09; 2.4、执行sql 1. 预处理&#xff08;Preprocessor&#xff09; 2. 查询优化器&#xff08;Optimizer&#xff09; 3. 执行器…...

编程新知 2026/2/7 5:16:05