算法刷题笔记 高精度除法(C++实现)
文章目录
- 题目描述
- 求解思路
- 实现代码
题目描述
- 给定两个非负整数(不含前导0)
A,B,请你计算A/B的商和余数。
输入格式
- 共两行,第一行包含整数A,第二行包含整数B。
输出格式
- 共两行,第一行输出所求的商,第二行输出所求余数。
数据范围
1 ≤ A的长度 ≤ 100000。1 ≤ B ≤ 10000。- B一定不为 0
求解思路
本题的求解思路仍然是通过编程模拟除法的竖式计算,但是和加减乘法又不一样的地方。由于除法竖式计算中,是从被除数的最高位开始,因此,存放被除数的数组应该用小端存放高位,大端存放低位。最后,和之前的 高精度减法 和 高精度乘法 两道算法题类似,最后的结果需要去除前导零。
实现代码
#include <iostream>
#include <vector>
using namespace std;vector<int> div(const vector<int>& a, const int& b)
{vector<int> result;int jinwei(0);for(int i(0); i < a.size(); ++i){int beichushu = a[i] + 10 * jinwei;result.push_back(beichushu / b);jinwei = beichushu % b;}result.push_back(jinwei);return result;
}int main(void)
{//变量定义部分string a;int b;vector<int> a_vector;//变量输入部分cin >> a >> b;for(int i(0); i < a.length(); ++i) a_vector.push_back(a[i] - '0');//除法运算并去除前导零部分vector<int> result = div(a_vector, b);while(result[0] == 0 && result.size() > 2) result.erase(result.begin());//变量输出部分for(int i(0); i < result.size() - 1; ++i) cout << result[i];cout << endl << result[result.size() - 1];return 0;
}
注意事项:
- 本题中要求同时输出商和余数,但是C++中只能一次返回一个变量,所以本题中将返回向量的最后一个元素设置为余数。实际使用过程中,可以为
div函数传入一个新的整数引用类型的参数r,这样,在div函数中修改r,则主函数中的r的值也会随之变化,从而解决了一次只能返回一个值的问题。
相关文章:
)
算法刷题笔记 高精度除法(C++实现)
文章目录 题目描述求解思路实现代码 题目描述 给定两个非负整数(不含前导0)A,B,请你计算 A/B 的商和余数。 输入格式 共两行,第一行包含整数A,第二行包含整数B。 输出格式 共两行,第一行输…...

按月爬取天气数据可视化展示
从天气网分析,可以查询每个月的天气情况,这里按照url规则,传入年月,获取数据,最后进行可视化展示,最终效果: 下面是获取过程: 第一步: import requestsdef get_weather(month):url = f"https://lishi.tianqi.com/nanning/{month}.html"response = reques…...

VMware安装Ubuntu系统(超详细)
一.Ubuntu官网下载镜像 Ubuntu官网:Enterprise Open Source and Linux | Ubuntu 二.安装Ubuntu系统 选择文件->创建虚拟机新建虚拟机(ControlN),这里直接选择典型即可 选择稍后安装系统 选择linux Ubuntu 64位 填写虚拟机名称…...

数据清洗操作及众所周知【数据分析】
各位大佬好 ,这里是阿川的博客 , 祝您变得更强 个人主页:在线OJ的阿川 大佬的支持和鼓励,将是我成长路上最大的动力 阿川水平有限,如有错误,欢迎大佬指正 前面的博客 数据分析—技术栈和开发环境搭建 …...
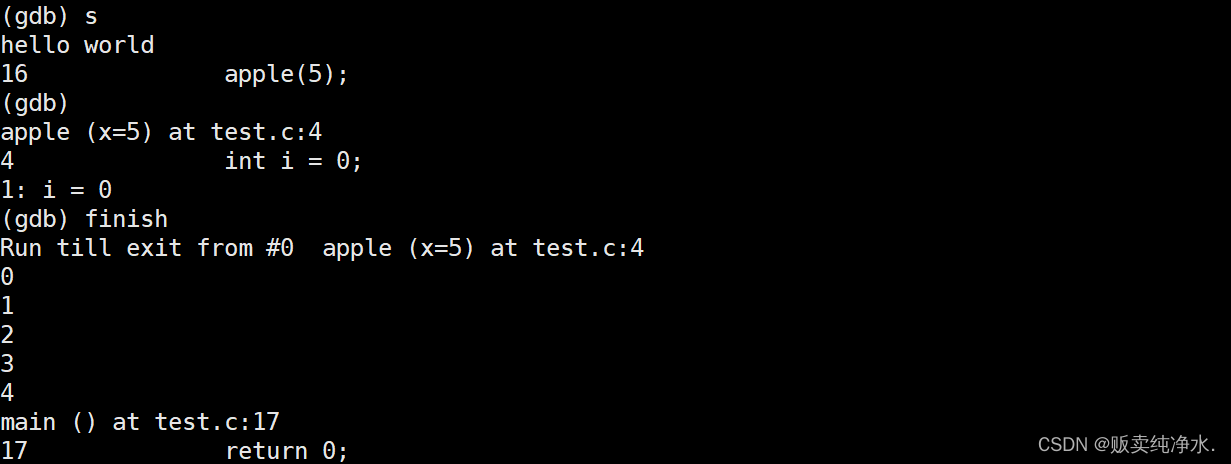
炫酷gdb
在VS里面调试很方便对吧?(F5直接调试,F10逐过程调试--不进函数,F11逐语句调试--进函数,F9创建断点),那在Linux中怎么调试呢? 我们需要用到一个工具:gdb 我们知道VS中程…...
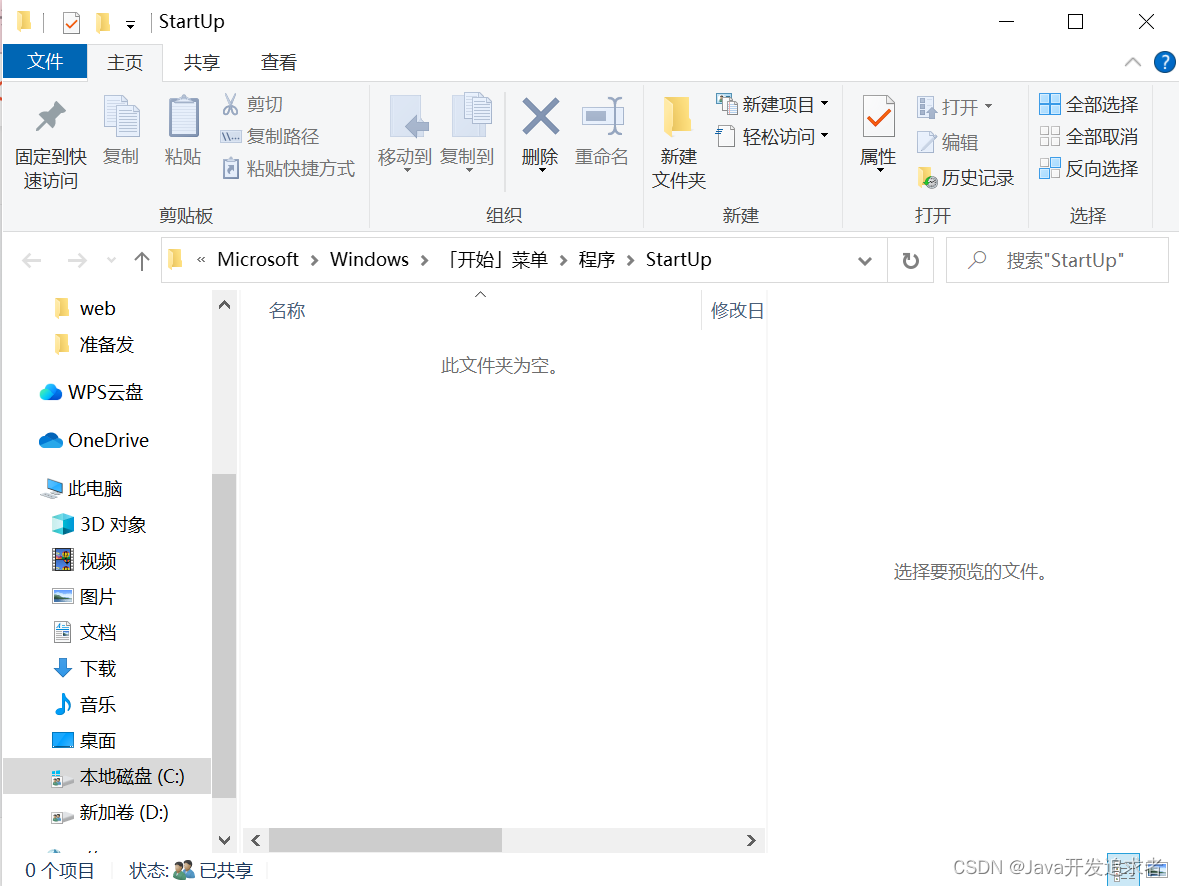
windows 7 10 11快捷键到启动页面
1.快速打开用户启动文件夹 shell:startup 方式2:快速打开系统启动文件夹 shell:Common Startup shell:Common Startup...

[处理器芯片]-6 超标量CPU实现之浮点运算
1 浮点运算单元FPU 超标量CPU中的浮点运算单元是专门处理浮点数运算的关键组件。浮点运算单元的设计涉及多个复杂的子模块和技术,以保证高效、准确地执行浮点数的加减法、乘法、除法、平方根等操作。 1)浮点数术语 浮点数通常采用IEEE 754标准表示&…...
又有人叫嚣:AI取代前端,来给你几张图,看能不能憋死AI。
总有自媒体人,为了些许流量,在大放厥词,说截个图给AI,AI就能输出前端代码,这是啥都敢说,吹牛不上税。 我来给你几张贝格前端工场日常接的大数据项目相关的图,你让AI生成代码,取代前…...

ISCC2024个人挑战赛WP-WEB
(非官方解,以下内容均互联网收集的信息和个人思路,仅供学习参考) 还没想好名字的塔防游戏 GET /world.js HTTP/1.1 Host: 101.200.138.180:17345 Accept: text/html,application/xhtmlxml,application/xml;q0.9,image/avif,i…...
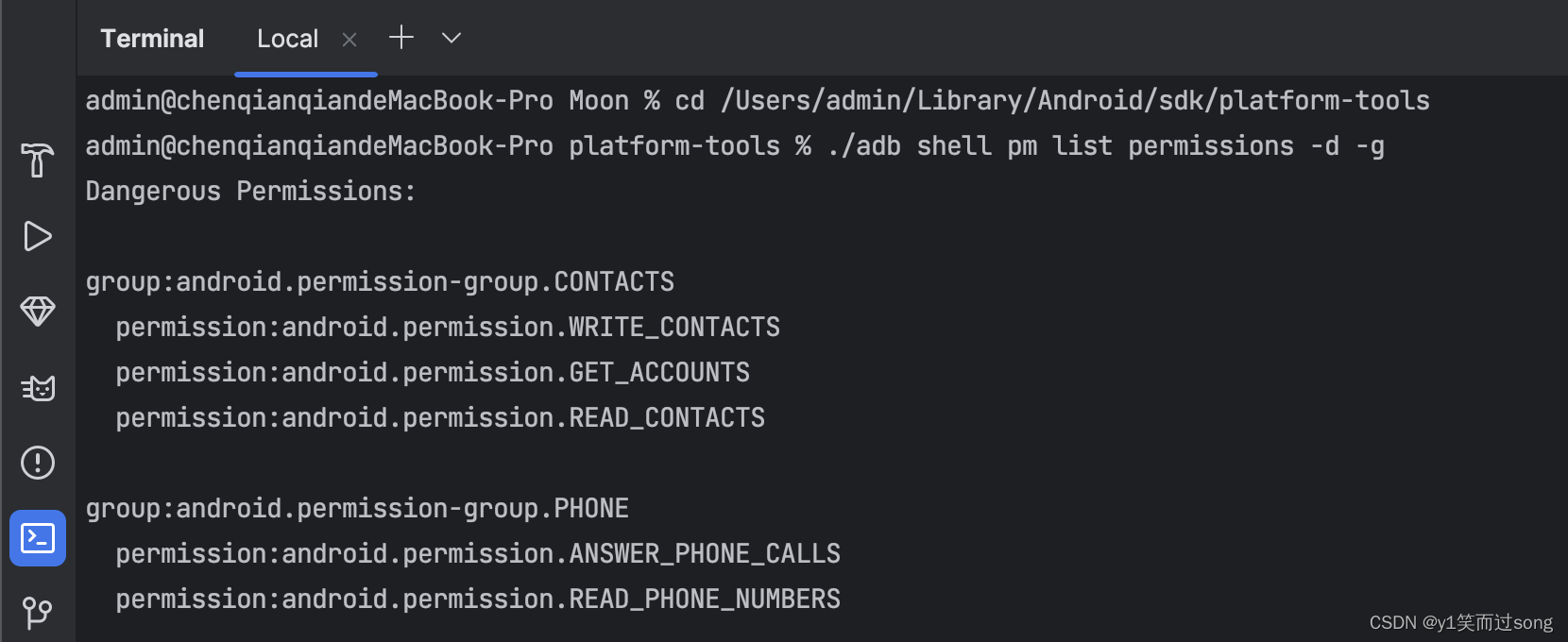
Android 使用 adb 列出设备上所有危险权限
步骤1:确定 Android SDK 位置 打开 Android Studio 的设置,并来到 Languages & Frameworks › Android SDK 处: 这里可以看到 Android SDK 目录的位置: 例如:/Users/admin/Library/Android/sdk。 复制这个路径&am…...

Spring AOP源码分析
#### AOP(面向切面编程)作用及其优势 作用:在程序运行期间,在不修改源码的情况下对方法进行功能增强(通知) 优势:减少重复代码,提高代码复用性,提高代码可维护性…...
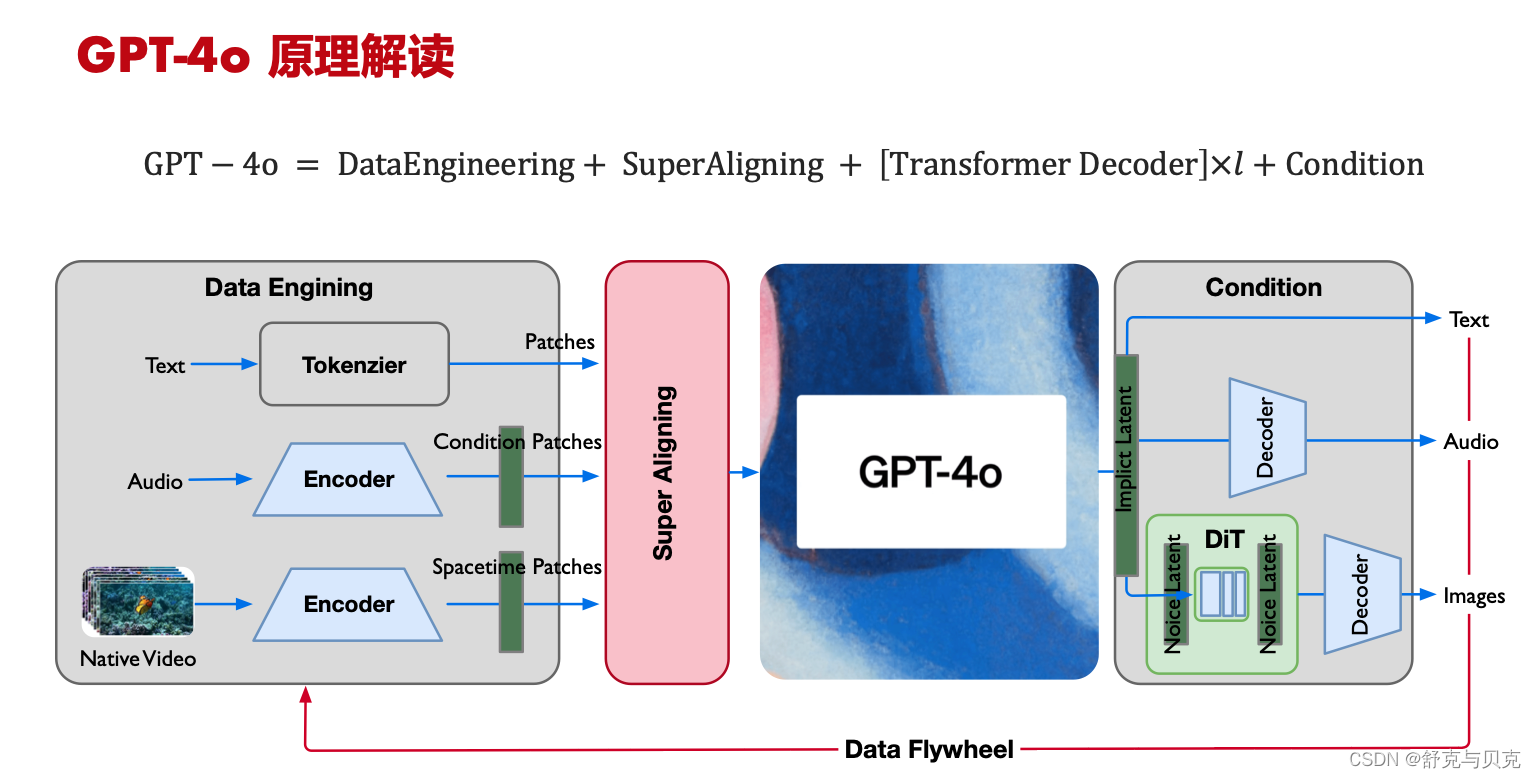
[LLM]从GPT-4o原理到下一代人机交互技术
一 定义 GPT-4o作为OpenAI推出的一款多模态大型语言模型,代表了这一交互技术的重要发展方向。 GPT-4o是OpenAI推出的最新旗舰级人工智能模型,它是GPT系列的一个重要升级,其中的"o"代表"Omni",中文意思是“全…...
)
【Spring】AOP——通知(Advice)
1、通知(Advice) 1.1简介 在AOP中,通知(Advice)是切面(Aspect)中的一部分,用于定义在连接点(Joinpoint)处应该执行的操作。通知类型可以在AOP框架中配置和使…...

python中的一些基础概念
在python中整型数据可以和浮点型数据相加,在python中字符串数据可以进行相加, 在python中整型数据可以和布尔类型进行算术运算。此时True当做1,False当做0但是这样的操作是没有意义的, python中只有字符串类型没有字符类型&…...

8.Redis之hash类型
1.hash类型的基本介绍 哈希表[之前学过的所有数据结构中,最最重要的] 1.日常开发中,出场频率非常高. 2.面试中,非常重要的考点, Redis 自身已经是键值对结构了Redis 自身的键值对就是通过 哈希 的方式来组织的 把 key 这一层组织完成之后, 到了 value 这一层~~ value 的其中…...

Edge浏览器
微软 Edge 是由微软开发的网络浏览器,它是 Windows 10 操作系统的默认浏览器,取代了之前的 Internet Explorer。Edge 浏览器在设计上注重性能、安全性和易用性,同时也提供了许多实用的功能,如内置笔记、阅读视图、集成的语音助手等…...

springboot项目中图片上传之后需要重启工程才能看到图片?
需求背景 最近在做一个用户自定义上传头像的小需求,用户上传头像然后需要立马回显。 需求是很常见的、正当的需求。如果不使用到对象存储这类服务,我们把用户头像的图片文件仅存在本地就可以了。我们在开发的过程中为了工程管理方便通常下意识会将图片…...

打卡信奥刷题(20)用Scratch图形化工具信奥B3756 [信息与未来 2021] 幸运数字
本题的基础是进制转换,关于2进制转换可以参考打卡信奥刷题(19)用Scratch图形化工具信奥B3972 [语言月赛 202405] 二进制 题解 知道了2进制,来实现5进制、7进制、9进制是一样的。 [信息与未来 2021] 幸运数字 题目描述 如果⼀个…...
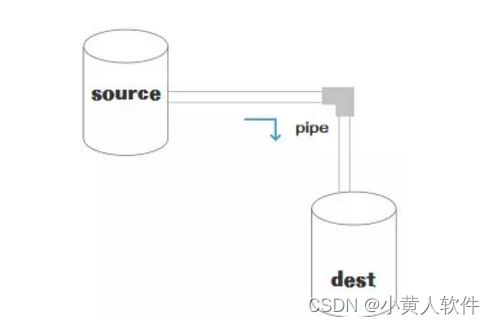
Stream流模式通信及示例
Stream流模式通信是指在计算机网络中,数据作为连续的字节流传输而不是独立的数据包。它是一种面向连接的通信方式,常见于TCP(传输控制协议)。以下是Stream流模式通信的基本概念和一个简单的示例。 基本概念 面向连接࿱…...
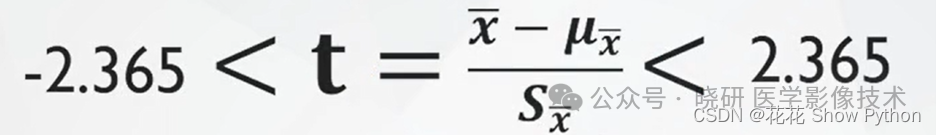
从0开始学统计-t分布
1.t分布是如何被发现的? t分布最早由英国统计学家威廉塞弗顿(William Sealy Gosset)在1908年提出。塞弗顿是爱尔兰的一名酿酒厂的统计学家,他的工作需要对小样本数据进行分析。由于当时样本量较小(通常小于30…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
