day12
第一题
本题我们可以使用以下方法:
方法一:
使用hash表<元素,出现次数>来统计字符串中不同元素分别出现的次数,当某一个元素的次数大于1时,返回false,如果每个元素的出现次数都为1,则返回true;
方法二:
对于hash表我们首先可以优化为int【】数组,最后我们可以继续优化为位图;
我们采用位图的思想和以下列操作来解决上述问题:
首先定义个位图变量,同时在32个位上,从右往左一次定义位置为0到31,并从右到左一次存放a,b。。。。。。等字符,最后进行位操作;
当我们在元素的相应定义位置进行与1操作,如果结果得到1,则已经存放过该元素了,直接返回false;反之得到的结果为0,则代表右新的元素出现时,位图的相应定义位置进行或1操作,并继续进行循环操作;直到循环结束;
综上所述,代码如下:
class Solution {public boolean isUnique(String str) {if(str.length() > 26){return false;}int bitMap = 0;for(int i = 0;i<str.length();i++){int x = str.charAt(i) - 'a';if(((bitMap >> x )& 1) == 1){return false;}else{bitMap = bitMap | (1 << x);}}return true;} }
第二题
本题采用位运算的方法来解决:
解题思路,让我们新定义的数组中的每一个数字和原始数组中的每一个数进行异或,最终的得到的数就是原始数组中缺少的那个数字:
举例如下:
代码如下所示:
class Solution {public int missingNumber(int[] nums) {int ret = 0;for(int x : nums) {ret ^= x; }for(int i = 0;i<=nums.length;i++){ret ^= i;}return ret;} }
第三题
解题过程如下图所示:
步骤一:
由于异或可以理解为无进位相加,可算出没有进位的两数相加;
步骤二:
由上图所示,两个数进行与操作,就可以得到需要进位的数字,只不过这个与的值需要左移一位;
举个例子,详细过程如下所示:
需要重复进行两个数的异或操作和取得进位数操作,直到需要加的进位数为0,此时就停止循环,代码如下所示:
class Solution {public int getSum(int a, int b) {while(b != 0){int x = a ^ b;int y = (a & b) << 1;a = x;b = y; }return a;} }
第四题
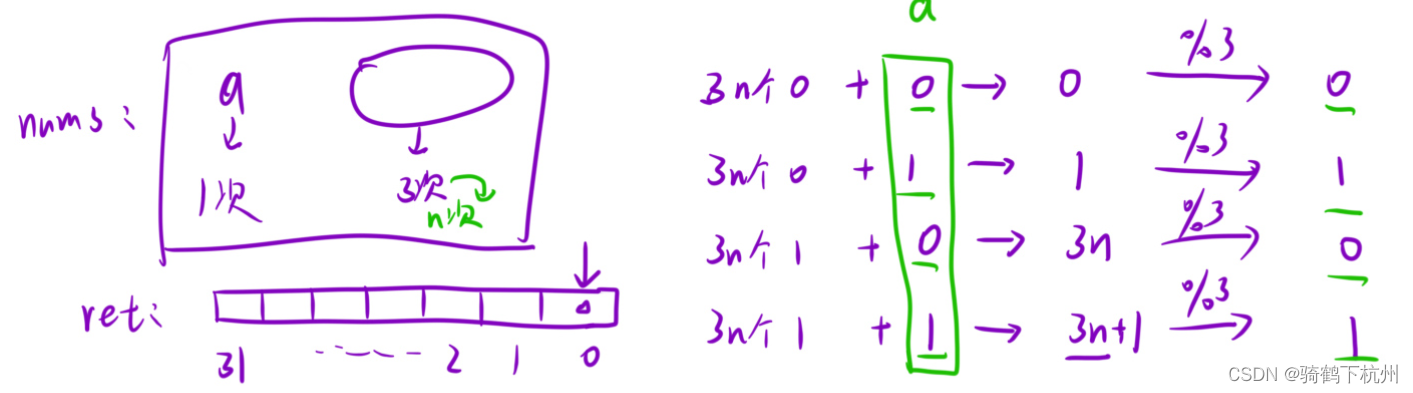
将原数组中的每一个元素进行位图存放,然后计算多个元素的同一个位置上的数字之和,将这些和余3,如下图所示:
最终每一个位置上存放被余到的数字,最终这些个数组成我们要求的出现一个的数;
代码如下所示:
class Solution {public int singleNumber(int[] nums) {int ret = 0;for(int i = 0;i<32;i++){int sum = 0;for(int x : nums){if(((x >> i) & 1) == 1){sum++;}sum %= 3;}if(sum ==1){ret = ret | (1 << i);}}return ret;}
}ps:本次的内容就到这里了,如果大家感兴趣的话就请一键三连哦!!!
相关文章:
day12
第一题 本题我们可以使用以下方法: 方法一: 使用hash表<元素,出现次数>来统计字符串中不同元素分别出现的次数,当某一个元素的次数大于1时,返回false,如果每个元素的出现次数都为1,则返回…...

MySQL技术点合集
目录 1. MySQL目录 2. 验证是否首次登陆方法 3. 在Liunx中使用命令来输入sql语句方法 4. 获取修改密码 5. 关闭密码策略 6. 忘记MySQL密码找回 7. 旋转90度横向查看表 8. 添加一个远程连接的用户 1. MySQL目录 /usr/bin/mysql相关命令vim /etc/my.cnfmysql配置文件ls /…...

记录使用 Vue3 过程中的一些技术点
1、自定义组件,并使用 v-model 进行数据双向绑定。 简述: 自定义组件使用 v-model 进行传参时,遵循 Vue 3 的 v-model 机制。在 Vue 3 中,v-model 默认使用了 modelValue 作为 prop 名称,以及 update:modelValue 作为…...

6. C++通过fork的方式实现高性能网络服务器
我们上一节课写的tcp我们发现只有第一个与之连接的人才能收发信息。他又很多的不足 高性能网络服务器 通过fork实现高性能网络服务器 我们通过fork进行改装之后就可以成百上千的用户进行连接访问,对于每一个用户来说我们都fork一个子进程。让后让每一个子进程都是…...

直播美颜插件、美颜SDK详解:技术、功能与实现原理
今天,小编将详细解析直播美颜插件和美颜SDK的技术、功能以及实现原理。 一、美颜技术的背景与发展 1.1美颜技术的兴起 随着直播平台的普及,美颜SDK技术逐渐被集成到直播软件中,以满足用户对更美观、自然的直播效果的需求。 1.2美颜技术的…...

MyBatis入门(1)
目录 一、JDBC操作回顾 二、什么是MyBatis? 三、MyBatis入门 1、准备工作 (1)创建工程 (2)数据准备 2、配置数据库连接字符串 3、写持久层代码 4、单元测试 (1)使用IDEA自动成成测试类…...

打开服务器远程桌面连接不上,可能的原因及相应的解决策略
在解决远程桌面连接不上服务器的问题时,我们首先需要从专业的角度对可能的原因进行深入分析,并据此提出针对性的解决方案。以下是一些可能的原因及相应的解决策略: 一、网络连接问题 远程桌面连接需要稳定的网络支持,如果网络连接…...
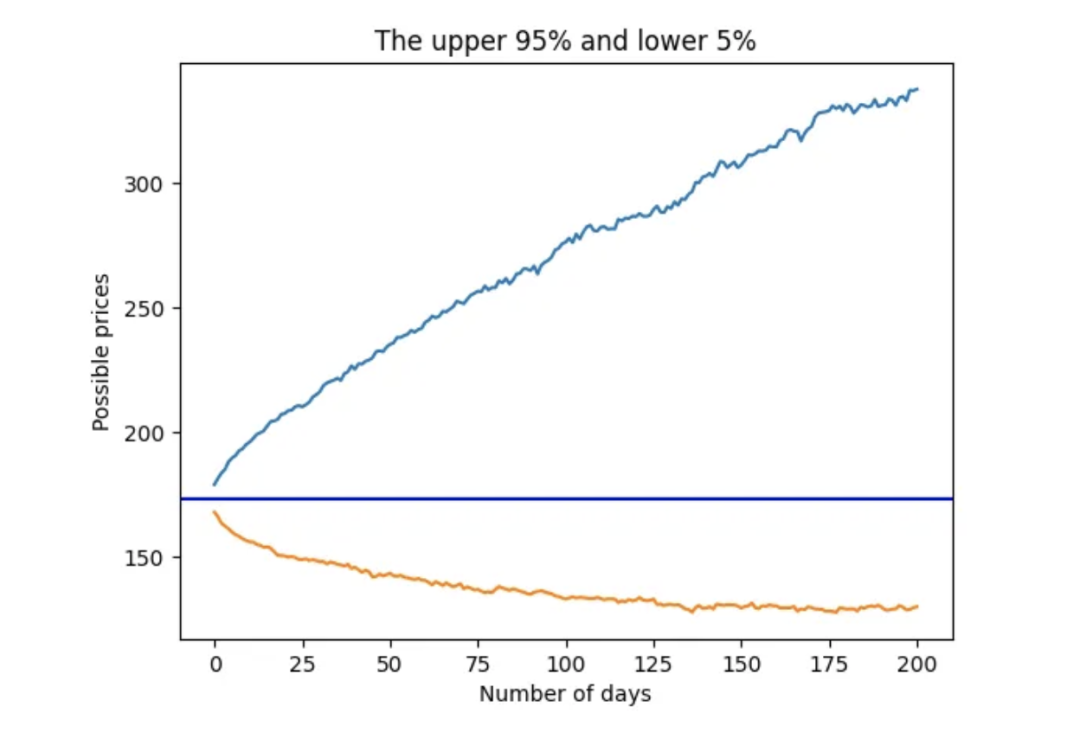
用于时间序列概率预测的蒙特卡洛模拟
大家好,蒙特卡洛模拟是一种广泛应用于各个领域的计算技术,它通过从概率分布中随机抽取大量样本,并对结果进行统计分析,从而模拟复杂系统的行为。这种技术具有很强的适用性,在金融建模、工程设计、物理模拟、运筹优化以…...

VScode解决报错“Remote-SSH XHR failed无法访问远程服务器“的方案
VScode解决报错"Remote-SSH XHR failed无法访问远程服务器"的方案 $ ls ~/.vscode-server/bin 2ccd690cbff1569e4a83d7c43d45101f817401dc稳定版下载链接:https://update.code.visualstudio.com/commit:COMMIT_ID/server-linux-x64/stable 内测版下载链接…...
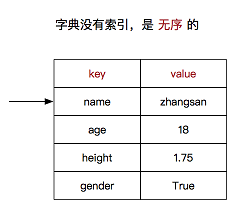
Python高级进阶--dict字典
dict字典⭐⭐ 1. 字典简介 dictionary(字典) 是 除列表以外 Python 之中 最灵活 的数据类型,类型为dict 字典同样可以用来存储多个数据字典使用键值对存储数据 2. 字典的定义 字典用{}定义键值对之间使用,分隔键和值之间使用:分隔 d {中…...
记忆力和人才测评,如何提升记忆力?
什么是记忆力? 如何通俗意义上的记忆力?我们可以把人的经历、经验理解成为一部纪录片,那么已经过去发生的事情,就是影片之前的情节,对于这些信息,在脑海里,人们会将其进行处理和组合ÿ…...

数据仓库建模
目录 数仓建模 为什么要对数据仓库进行分层 主题 主题的概念 维度建模: 模型的选择: 星形模式 雪花模型 星座模式 拉链表 维度表和事实表: 维度表 事实表 事实表设计规则 退化维度 事务事实表、周期快照事实表、累积快照事实…...

力扣:1738. 找出第 K 大的异或坐标值
1738. 找出第 K 大的异或坐标值 给你一个二维矩阵 matrix 和一个整数 k ,矩阵大小为 m x n 由非负整数组成。 矩阵中坐标 (a, b) 的 值 可由对所有满足 0 < i < a < m 且 0 < j < b < n 的元素 matrix[i][j](下标从 0 开始计数&…...

Keras深度学习框架第二十讲:使用KerasCV中的Stable Diffusion进行高性能图像生成
1、绪论 1.1 概念 为便于后文讨论,首先进行相关概念的陈述。 Stable Diffusion:Stable Diffusion 是一个在图像生成领域广泛使用的技术,尤其是用于文本到图像的转换。它基于扩散模型(Diffusion Models),这…...

C/C++ vector详解
要想了解STL,就必须会看: cplusplus.comhttps://legacy.cplusplus.com/ 官方内容全都是英文的,可以参考: C/C初始识https://blog.csdn.net/2301_77087344/article/details/138596294?spm1001.2014.3001.5501 vectorÿ…...

使用libtorch加载YOLOv8生成的torchscript文件进行目标检测
在网上下载了60多幅包含西瓜和冬瓜的图像组成melon数据集,使用 LabelMe 工具进行标注,然后使用 labelme2yolov8 脚本将json文件转换成YOLOv8支持的.txt文件,并自动生成YOLOv8支持的目录结构,包括melon.yaml文件,其内容…...
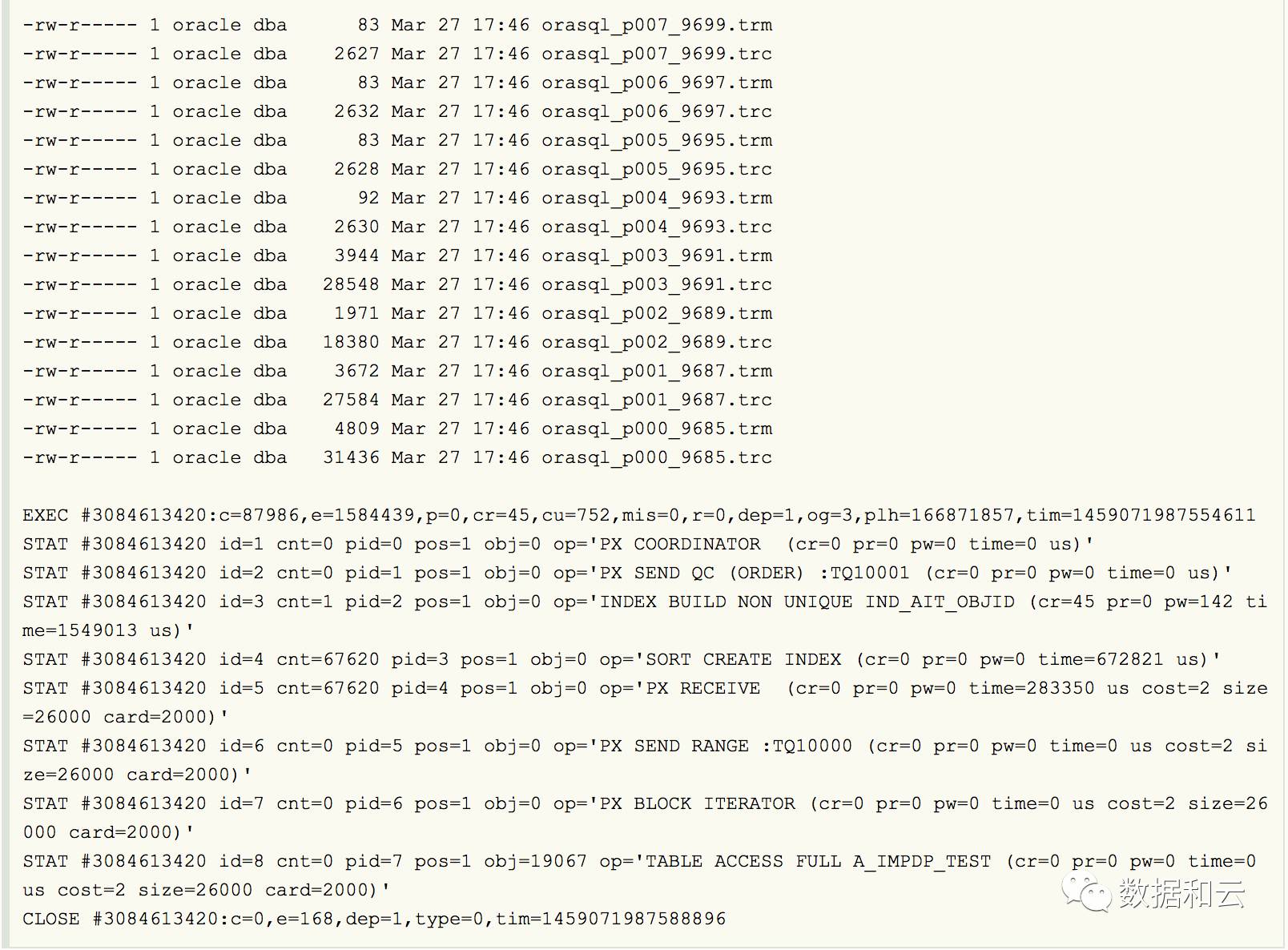
Oracle 并行和 session 数量的
这也就是为什么我们指定parallel为4,而实际并行度为8的原因。 insert create index,发现并行数都是加倍的 Indexes seem always created with parallel degree 1 during import as seen from a sqlfile. The sql file shows content like: CREATE INDE…...

Android 版本与 API level 以及 NDK 版本对应
采用 Android studio 开发 Android app 的时候,需要选择支持的最低 API Level 和使用的 NDK 版本,对应开发 app 的最低 SDK 版本: 在 app 的 build.gradle 文件里,对应于代码如下: 目前各版本的占有率情况如下…...

护网经验面试题目原版
文章目录 一、护网项目经验1.项目经验**Hvv的分组和流程**有没有遇到过有意思的逻辑漏洞?有没有自己开发过武器/工具?有做过代码审计吗?有0day吗有cve/cnvd吗?有src排名吗?有没有写过技战法有钓鱼经历吗?具…...
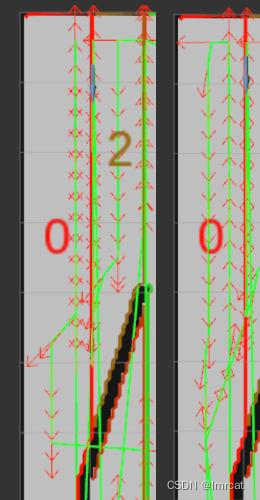
ipa 覆盖算法测试
相关文章 ipa 功能包测试 ipa 分区算法 ipa 分区算法总结,部分算法图解 ipa 覆盖算法分析(一) ipa 覆盖算法分析(二) 测试 网上找的地图: fig.1 测试地图 opencv fig.2 opencv 显示的覆盖路径 rviz fi…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...