【C语言】二叉树的实现
文章目录
- 前言
- ⭐一、二叉树的定义
- 🚲二、创建二叉树
- 🎡三、二叉树的销毁
- 🎉四、遍历二叉树
- 1. 前序遍历
- 2. 中序遍历
- 3. 后序遍历
- 4. 层序遍历
- 🌲五、二叉树的计算
- 1. 计算二叉树结点个数
- 2. 计算二叉树叶子结点的个数
- 3. 计算二叉树的深度
- 4. 计算二叉树第k层的结点个数
- 5. 查找二叉树中值为x的结点
- 6. 判断二叉树是否为完全二叉树
- 🏝️六、整体代码展示
前言
在学习二叉树实现时,我们首先要对二叉树基本认识有一定的了解,下面我总结了以下几点有关二叉树的性质以及特点:
🎈每一个节点最多有两棵子树,不存在度大于2的节点。
🎈左右子树是有顺序的,其次序不能颠倒。
🎈二叉树一般有四种形态,分别为:空二叉树,只有一个根节点,根结点只有左子树和根节点只有右子树。
🎈二叉树常用的三种性质:1)二叉树的第 i 层上最多有2 ^ (i - 1)个节点;
2)深度为K的二叉树最多有2 ^ (k - 1)个节点。
3)度为0的节点个数比度为2的节点个数多一个。
⭐一、二叉树的定义
二叉树通常以结构体的形式定义,其结构体内容包括三部分:本节点所存储的值、左孩子节点的指针以及右孩子节点的指针。这里需要注意,子节点必须使用指针,就像我们定义结构体链表一样,下一个节点必须使用地址的方式存在在结构体当中。
typedef int BTDateType;typedef struct BinaryTreeNode
{BTDateType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
🚲二、创建二叉树
当我们对二叉树的掌握还不够深入时,我们也可以创建一棵简单的二叉树,减少时间成本。
// 手搓一个二叉树
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
而真正的二叉树创建的过程是这样的:首先给出一个数组,将要创建的元素放在数组里。然后通过遍历(前 或 中 或 后序遍历)的顺序访问并创建二叉树每个节点,最后返回根节点的地址即创建完成。
我们假设通过前序序列的方式访问并创建二叉树:
// 创建树,按前序遍历的顺序
BTNode* BinaryTreeCreate(BTDateType* a, int* pi) {if (a[*pi] != '#') // '#'代表叶子结点{BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->data = a[*pi];(*pi)++;root->left = BinaryTreeCreate(a, pi);(*pi)++;root->right = BinaryTreeCreate(a, pi);return root;}else {return NULL;}
}
🎡三、二叉树的销毁
// 销毁
void BinaryTreeDestory(BTNode* root)
{if (root){BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);root = NULL;}
}
🎉四、遍历二叉树
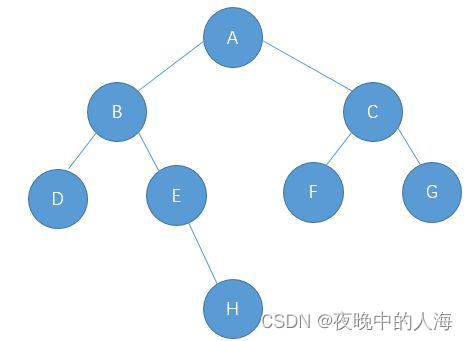
前序遍历,中序遍历和后序遍历,实际上就是指根节点在子节点的先中后的顺序不同。以上图为例:
前序序列:A、B、D、E、H、C、F、G
中序遍历:D、B、H、E、A、F、C、G
后序遍历:D、H、E、B、F、G、C、A
这三种遍历方式,在代码上面还是非常相似的,只不过递归的顺序不同。
1. 前序遍历
先遍历根结点,再遍历左子树,最后遍历右子树。
// 前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N "); //打印空节点数据return;}printf("%d ", root->data); // 输出节点数据PrevOrder(root->left); //递归遍历左子树节点的数据PrevOrder(root->right); //递归遍历右子树节点的数据
}
2. 中序遍历
先遍历左子树,再遍历根结点,最后遍历右子树。
// 中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N "); //打印空节点数据return;}InOrder(root->left); //递归遍历左子树节点的数据printf("%d ", root->data); //输出节点数据InOrder(root->right); //递归遍历右子树节点的数据
}
3. 后序遍历
先遍历左子树,再遍历右子树,最后遍历根结点。
// 后序遍历
void EndingepilogueOrder(BTNode* root)
{if (root == NULL){printf("N "); //打印空节点数据return;}EndingepiloguePrevOrder(root->left); //递归遍历左子树节点的数据EndingepiloguePrevOrder(root->right); //递归遍历右子树节点的数据printf("%d ", root->data); //输出节点数据
}
4. 层序遍历
层序遍历的做法和上述遍历做法不同,不能简单的调用递归来遍历,而是要借用到队列来辅助实现。队列的实现我就不在叙述了,层序遍历代码所示:
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root); //存入根节点}while (!QueneEmpty(&q)) //队列不为空就循环{BTNode* front = QueneFront(&q); //取出队列中的第一个节点QuenePop(&q); //删除第一个节点printf("%d ", front->data); //打印取出来第一个节点的数据if (front->left){QuenePush(&q, front->left); //如果左子树不为空,就将左子树存入队列}if (front->right){QuenePush(&q, front->right); //如果右子树不为空,就将右子树存入队列}}QueneDesTroy(&q);
}
🌲五、二叉树的计算
1. 计算二叉树结点个数
计算二叉树的结点个数,只需要将左子树的结点个数加上右子树的结点个数,最后再加上根结点就完成了。
int TreeSide(BTNode* root)
{return root == NULL ? 0 : TreeSide(root->left) + TreeSide(root->right) + 1; //运用条件表达式,如果根结点为空就返回0,否则就递归调用遍历左子树和右子树的结点个数,两者相加,最后再加一个最上面的根结点。
}
2. 计算二叉树叶子结点的个数
首先要明白什么是叶子结点,实际上就是度为0的结点即孩子结点。
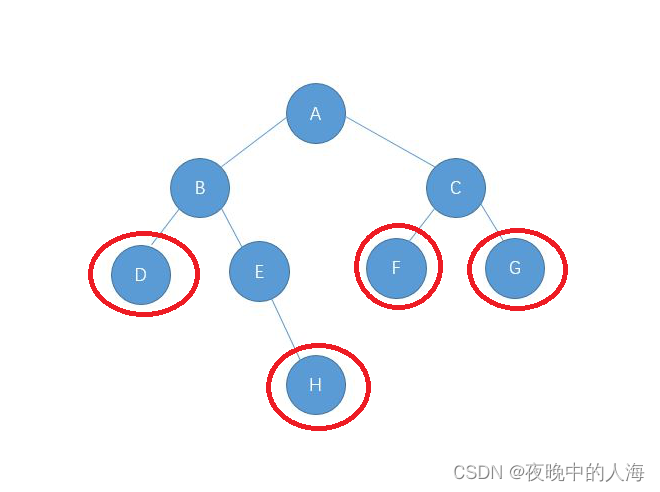
如上图,D、H、F、G都为叶子结点。代码展示:
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0; //空树返回0}else if (TreeLeafSize(root->left)== NULL && TreeLeafSize(root->right) == NULL){return 1; //只含有根节点就返回1}return TreeLeafSize(root->left) + TreeLeafSize(root->right); ///递归调用遍历左子树和右子树的叶子数,两者相加
}
3. 计算二叉树的深度
什么是二叉树的深度呢?简单的来说就是左子树或者右子树的深度+1。
// 求树的深度
int TreeHight(BTNode* root)
{if (root == NULL){return 0;}int highleft = TreeHight(root->left); //获取左子树的深度int highright = TreeHight(root->right); //获得右子树的深度return highleft > highright ? highleft + 1 : highright + 1; //运用条件表达式,返回左子树和右子树中较大的深度+1
}
4. 计算二叉树第k层的结点个数
实现这一操作的核心思路,就是要知道:求当前树的第k层结点个数 = 左子树的第k - 1层的结点个数 + 右子树的第k-1层的结点个数。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0; // 空树返回0}if (k == 1){return 1; //第一层为根节点返回1}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
5. 查找二叉树中值为x的结点
这里需要注意的是,我们要记录查找到的结点,否则当我们想要返回所找到的结点数据,却发现又要重新递归去找,时间会消耗好几倍,因此需要记录找到的结点数据
BTNode* BinaryTreeFind(BTNode* root, BTDateType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* left = BinaryTreeFind(root->left, x);if (left != NULL)return left;BTNode* right = BinaryTreeFind(root->right, x);if (right != NULL)return right;// 左右子树都没有return NULL;
}
6. 判断二叉树是否为完全二叉树
按照层序遍历的方式遍历完全二叉树,当我们遍历到空结点时,就开始判断。如果队列中还有空,就不是完全二叉树
// 判断二叉树是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 遇到第一个空就开始判断,如果队列中还有空,就不是完全二叉树if (front == NULL){break;}QuenePush(&q, front->left);QuenePush(&q, front->right);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 如果有非空,就不是完全二叉树if (front){QueneDesTroy(&q);return false;}}QueneDesTroy(&q);return true;
}
🏝️六、整体代码展示
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include "Quene.h"typedef int BTDateType;typedef struct BinaryTreeNode
{BTDateType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 手搓一个二叉树BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}// 销毁
void BinaryTreeDestory(BTNode* root)
{if (root){BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);root = NULL;}
}// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);printf("%d ", front->data);if (front->left){QuenePush(&q, front->left);}if (front->right){QuenePush(&q, front->right);}}QueneDesTroy(&q);
}// 前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}// 中序遍历
void InPrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InPrevOrder(root->left);printf("%d ", root->data);InPrevOrder(root->right);
}// 后序遍历
void EndingepiloguePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}EndingepiloguePrevOrder(root->left);EndingepiloguePrevOrder(root->right);printf("%d ", root->data);
}int TreeSide(BTNode* root)
{return root == NULL ? 0 : TreeSide(root->left) + TreeSide(root->right) + 1;
}// 求叶子结点的个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}else if (TreeLeafSize(root->left)== NULL && TreeLeafSize(root->right) == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}// 求树的深度
int TreeHight(BTNode* root)
{if (root == NULL){return 0;}int highleft = TreeHight(root->left);int highright = TreeHight(root->right);return highleft > highright ? highleft + 1 : highright + 1;
}// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDateType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* left = BinaryTreeFind(root->left, x);if (left != NULL)return left;BTNode* right = BinaryTreeFind(root->right, x);if (right != NULL)return right;// 左右子树都没有return NULL;
}// 判断二叉树是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 遇到第一个空就开始判断,如果队列中还有空,就不是完全二叉树if (front == NULL){break;}QuenePush(&q, front->left);QuenePush(&q, front->right);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 如果有非空,就不是完全二叉树if (front){QueneDesTroy(&q);return false;}}QueneDesTroy(&q);return true;
}int main()
{BTNode* root = CreatBinaryTree();PrevOrder(root);printf("\n");InPrevOrder(root);printf("\n");EndingepiloguePrevOrder(root);printf("\n");printf("TreeSide:%d\n", TreeSide(root));printf("TreeLeafSize:%d\n", TreeLeafSize(root));printf("TreeHight:%d\n", TreeHight(root));printf("BinaryTreeFind:%p\n", BinaryTreeFind(root,3));printf("BinaryTreeLevelKSize:%d\n", BinaryTreeLevelKSize(root, 3));printf("\n");BinaryTreeLevelOrder(root);return 0;
}
今天的分享就到这里啦,如果感觉内容不错,记得一键三连噢。创作不易,感谢大家的支持,我们下次再见!ヾ( ̄▽ ̄)ByeBye
相关文章:

【C语言】二叉树的实现
文章目录 前言⭐一、二叉树的定义🚲二、创建二叉树🎡三、二叉树的销毁🎉四、遍历二叉树1. 前序遍历2. 中序遍历3. 后序遍历4. 层序遍历 🌲五、二叉树的计算1. 计算二叉树结点个数2. 计算二叉树叶子结点的个数3. 计算二叉树的深度4…...

在ubuntu22.04里网站源码连不上mysql数据库
在ubuntu22.04里网站源码连不上mysql数据库。后来找到了原因。 连不上的时候有报错信息: ERROR 1698 (28000): Access denied for user rootlocalhost 用在网上搜索该报错信息,找到了两篇有用的文章,用这两篇文章里的处理方法解决了问题。 …...
博客说明 5/12~5/24【个人】
博客说明 5/12~5/24【个人】 前言版权博客说明 5/12~5/24【个人】对比最后 前言 2024-5-24 13:39:23 对我在2024年5月12日到5月24日发布的博客做一下简要的说明 以下内容源自《【个人】》 仅供学习交流使用 版权 禁止其他平台发布时删除以下此话 本文首次发布于CSDN平台 作…...

豆瓣电影后端设计
sql脚本 -- douban.tags_encode definitionCREATE TABLE tags_encode (id bigint NOT NULL AUTO_INCREMENT COMMENT 自增主键,tag varchar(100) NOT NULL COMMENT tag中文名,tag_encode varchar(100) NOT NULL COMMENT tag转encode,type varchar(100) NOT NULL DEFAULT movie …...

【深度学习】第1章
概论: 机器学习是对研究问题进行模型假设,利用计算机从训练数据中学习得到模型参数,并最终对数据进行预测和分析,其基础主要是归纳和统计。 深度学习是一种实现机器学习的技术,是机器学习重要的分支。其源于人工神经网络的研究。深度学习的模型结构是一种含多隐层的神经…...
Vue3实战笔记(37)—粒子特效登录页面
文章目录 前言一、粒子特效登录页总结 前言 上头了,再来一个粒子特效登录页面。 一、粒子特效登录页 登录页: <template><div><vue-particles id"tsparticles" particles-loaded"particlesLoaded" :options"…...

解锁无限可能:JavaScript与【机器学习】的浪漫邂逅
解锁无限可能:JavaScript与机器学习的浪漫邂逅 在人工智能和大数据日益盛行的今天,机器学习已成为我们理解、分析和处理数据的强大工具。而JavaScript,作为前端开发的主流语言,其灵活的特性和广泛的应用场景也让我们对其充满了期…...
中的内容与不加$()时有什么区别)
【Linux】$()中的内容与不加$()时有什么区别
$()中的内容与不加$()有什么区别,例如$(/usr/local/hadoop/bin/hadoop classpath)与/usr/local/hadoop/bin/hadoop classpath两者有何区别??? 关于这个问题,笔者建议可以参考如下文章: Linux—shell中$((…...

2024最新前端面试八股文【基础篇293题】
⼀、HTML、HTTP、web综合问题 1 前端需要注意哪些SEO 2 <img> 的 title 和 alt 有什么区别 3 HTTP的⼏种请求⽅法⽤途 4 从浏览器地址栏输⼊url到显示⻚⾯的步骤 5 如何进⾏⽹站性能优化 6 HTTP状态码及其含义 7 语义化的理解 8 介绍⼀下你对浏览器内核的理解 9 …...

【NumPy】关于numpy.median()函数,看这一篇文章就够了
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...

起保停电路工作原理
一、电路组成 起保停电路由电源保护设备(空气开关)、交流接触器、启动按钮、停止按钮和用电设备组成。 起保停电路的组成部分通常可分为四个部分: 保护部分:(空气开关)在电流或电压超出一定范围时自动切断…...

【Vue】Vue2使用ElementUI
目录 Element UI介绍特点Vue2使用Element安装引入ElementUI组件库 使用ElementUI用户注册列表展示其他 mint-ui介绍特点安装组件引入组件Mint-ui相关组件 Element UI 介绍 官网(基于 Vue 2.x ):https://element.eleme.cn/#/zh-CN ElementUI 是一个基于 Vue.js 的桌面端组件库…...

设计模式在芯片验证中的应用——模板方法
一、模板方法 模板方法(Template Method)设计模式是一种行为设计模式, 它在父类中定义了一个功能的框架, 允许子类在不修改结构的情况下重写功能的特定步骤。也就是模板方法定义了一组有序执行的操作,将一些步骤的实现留给子类,同…...

Webpack Bundle Analyzer:深入分析与优化你的包
Webpack Bundle Analyzer是一个用于可视化的工具,它可以帮助你分析Webpack打包后的输出文件,查看哪些模块占用了最多的空间,从而进行优化。 2500G计算机入门到高级架构师开发资料超级大礼包免费送! 首先,你需要安装W…...

Java后端开发学习历程
1、JavaWeb------------------------>19天 2、SSMSpringBoot------------->12天 3、瑞吉外卖项目------------------>15天 4、JavaSE-------------------------->25天 总耗时71天(2024.03.11——2024.05.26两个半月),Java后端…...

CentOS 7 socat命令端口转发
场景 开发排查问题需配置远程调试,但配置调试的服务器不支持外网访问,于是就考虑到用端口转发的方式让开发进行远程调试,转发工具比如有:rinetd等等,意外看到使用socat做转发更简单方便,下面就记录一下 命令简介 socat 是一个功能强大的网络工具,可以在两个连接的数据…...

vue全局修改设置滚动条样式
vue全局修改设置滚动条样式 具体代码: ::-webkit-scrollbar{ /*滚动条整体样式*/width: 6px; /*高宽分别对应横竖滚动条的尺寸*/height: 1px; } ::-webkit-scrollbar-thumb{ /*滚动条里面小方块*/border-radius: 5px;background: #cfcbcb; } ::-webkit-scrollbar-…...
✨聚梦AI绘图插件-for photoshop(基于ComfyUI) 内测版V0.1发布
🎈背景 photoshop本身是有AI生成能力的,不过限于种种原因,国内使用很不方便。 photoshop也是有AI插件的,不过大多安装起来比较复杂,或者,干脆就会收费。 所以我们做了一个免费的AI插件,期望能…...
java “错误:编码GBK 的不可映射字符”
环境:JDK-17 本机编码:utf-8 代码编码:GBK 错误:java “错误:编码GBK 的不可映射字符” 解决1:记事本打开java源文件,另存为选择ANSI编码 解决2:复制代码再将编码格式改为utf-8,…...
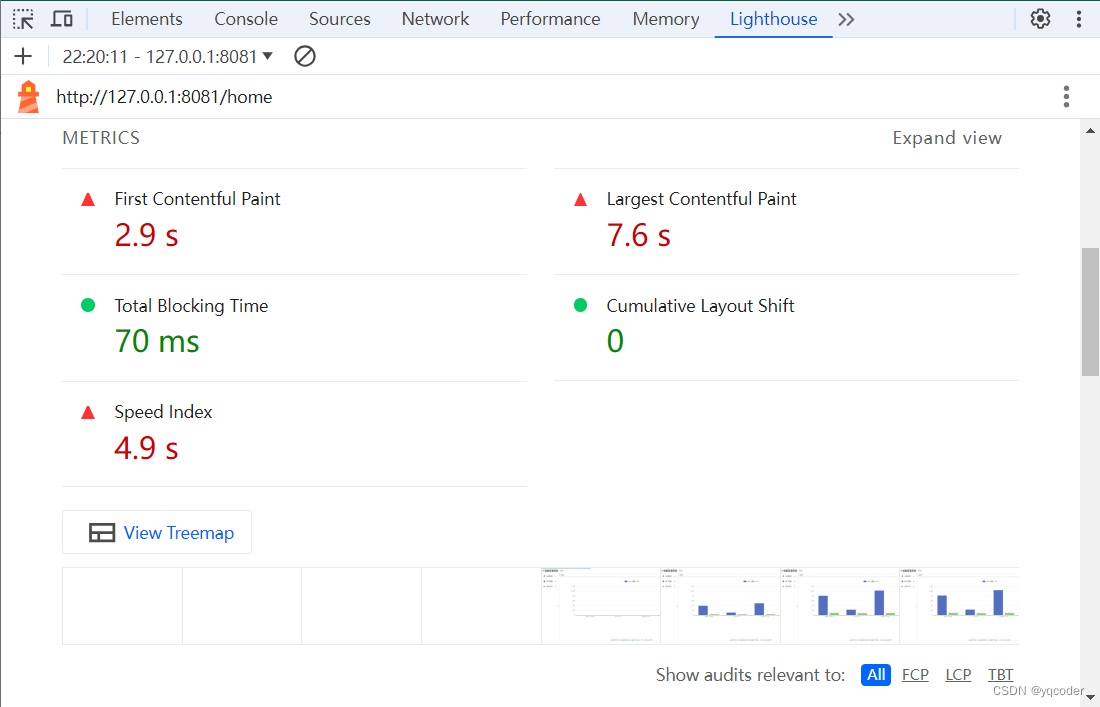
前端 JS 经典:Web 性能指标
什么是性能指标:Web Performance Metrics 翻译成 Web 性能指标,一般和时间有关系,在短时间内做更多有意义的事情。 一个站点表现得好与不好,标准在于用户体验,而用户体验好不好,有一套 RAIL 模型来衡量。这…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
