深度学习中的优化算法二(Pytorch 19)
一 梯度下降
尽管梯度下降(gradient descent)很少直接用于深度学习,但了解它是理解下一节 随机梯度下降算法 的关键。例如,由于学习率过大,优化问题可能会发散,这种现象早已在梯度下降中出现。同样地,预处理 (preconditioning)是梯度下降中的一种常用技术,还被沿用到更高级的算法中。让我们从简单的一维梯度 下降开始。
1.1 一维梯度下降
即在一阶近似中,f(x + ϵ)可通过x处的函数值f(x)和一阶导数f ′ (x)得出。我们可以假设在负梯度方向上移动 的ϵ会减少f。为了简单起见,我们选择固定步长η > 0,然后取ϵ = −ηf′ (x)。将其代入泰勒展开式我们可以得到。
因此,在梯度下降中,我们首先 选择初始值x和常数η > 0,然后使用它们 连续迭代x,直到停止条件达成。例如, 当梯度|f ′ (x)|的幅度足够小 或 迭代次数达到某个值 时。
下面我们来展示如何实现梯度下降。为了简单起见,我们选用目标函数f(x) = x^2。尽管我们知道x = 0时f(x)能 取得最小值,但我们仍然使用这个简单的函数来观察x的变化。
%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2ldef f(x):return x ** 2def f_grad(x):return 2 * x接下来,我们使用 x = 10作为初始值,并假设η = 0.2。使用梯度下降法 迭代x共10次,我们可以看到,x的值 最终将接近最优解。
def gd(eta, f_grad):x = 10.0result = [x]for i in range(10):x -= eta * f_grad(x)result.append(float(x))print(f'epoch 10, x: {x:f}')return result
results = gd(0.2, f_grad)
对进行x优化的过程可以绘制如下。
def show_trace(results, f):n = max(abs(min(results)), abs(max(results)))f_line = torch.arange(-n, n, 0.01)d2l.set_figsize()d2l.plot([f_line, results], [[f(x) for x in f_line], [f(x) for x in results]], 'x', 'f(x)', fmts = ['-', '-o'])show_trace(results, f)
1.1.1 学习率
学习率(learning rate)决定目标函数能否收敛到局部最小值,以及何时收敛到最小值。学习率η可由算法设 计者设置。请注意,如果我们使用的学习率太小,将导致 x的更新非常缓慢,需要更多的迭代。例如,考虑同 一优化问题中η = 0.05的进度。如下所示,尽管经过了10个步骤,我们仍然离最优解很远。
show_trace(gd(0.05, f_grad), f)
相反,如果我们使用过高的学习率,|ηf′ (x)|对于一阶泰勒展开式可能太大。也就是说,(11.3.1)中 的O(η 2f ′2 (x))可能变得显著了。在这种情况下,x的迭代不能保证降低f(x)的值。例如,当学习率为η = 1.1时, x超出了最优解x = 0并逐渐发散。
show_trace(gd(1.1, f_grad), f)

1.1.2 局部最小值
为了演示非凸函数的梯度下降,考虑函数f(x) = x · cos(cx),其中c为某常数。这个函数有无穷多个局部最小 值。根据我们选择的学习率,我们最终可能只会得到许多解的一个。下面的例子说明了(不切实际的)高学习率如何导致较差的局部最小值。
c = torch.tensor(0.15 * np.pi)def f(x):return x * torch.cos(c * x)def f_grad(x):return torch.cos(c * x) - c * x * torch.sin(c * x)show_trace(gd(2, f_grad), f)
1.2 多元梯度下降
现在我们对单变量的情况有了更好的理解,让我们考虑一下x = [x1, x2, . . . , xd] ⊤的情况。即目标函数f : R d → R将向量映射成标量。相应地,它的梯度也是多元的,它是一个由d个偏导数组成的向量。
换句话说,在ϵ的二阶项中,最陡下降的方向由负梯度−∇f(x)得出。选择合适的学习率η > 0来生成典型的梯 度下降算法:
我们还需要两个辅助函数:第一个是update函数,并将其应用于初始值20次;第二个函数会显示x的轨迹。
def train_2d(trainer, steps = 20, f_grad = None): #@savex1, x2, s1, s2 = -5, -2, 0, 0results = [(x1, x2)]for i in range(steps):if f_grad:x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)else:x1, x2, s1, s2 = trainer(x1, x2, s1, s2)results.append((x1, x2))print(f'epoch {i + 1}, x1: {float(x1): f}, x2: {float(x2): f}')return resultsdef show_trace_2d(f, results): #@saved2l.set_figsize()d2l.plt.plot(*zip(*results), '-o', color = '#ff7f0e')x1, x2 = torch.meshgrid(torch.arange(-5.5, 1.0, 0.1),torch.arange(-3.0, 1.0, 0.1), indexing = 'ij')d2l.plt.contour(x1, x2, f(x1, x2), colors = '#1f77b4')d2l.plt.xlabel('x1')d2l.plt.ylabel('x2')接下来,我们观察 学习率η = 0.1时优化变量x的轨迹。可以看到,经过20步之后,x的值接近其位于[0, 0]的最小值。虽然进展相当顺利,但相当缓慢。
def f_2d(x1, x2):return x1 ** 2 + 2 * x2 ** 2def f_2d_grad(x1, x2):return (2 * x1, 4 * x2)def gd_2d(x1, x2, s1, s2, f_grad):g1, g2 = f_grad(x1, x2)return (x1 - eta * g1, x2 - eta * g2, 0, 0)eta = 0.1
show_trace_2d(f_2d, train_2d(gd_2d, f_grad = f_2d_grad))1.2.1 自适应方法
选择“恰到好处”的学习率η是很棘手的。如果我们把它选得太小,就没有什么进展;如果太大,得到的解就会振荡,甚至可能发散。如果我们可以自动确定η,或者完全不必选择学习 率,会怎么样?除了考虑目标函数的值和梯度、还考虑它的曲率的二阶方法可以帮我们解决这个问题。虽然 由于计算代价的原因,这些方法不能直接应用于深度学习,但它们为如何设计高级优化算法提供了有用的思维直觉,这些算法可以模拟下面概述的算法的许多理想特性。
也就是说,作为优化问题的一部分,我们 需要将Hessian矩阵H求逆。
举一个简单的例子,对于f(x) = 1 / 2 x ^ 2,我们有∇f(x) = x和H = 1。因此,对于任何x,我们可以获得ϵ = −x。 换言之,单单一步就足以完美地收敛,而无须任何调整。我们在这里比较幸运:泰勒展开式是确切的,因 为f(x + ϵ) = 1/2 x^2 + ϵx + 1/2 ϵ^2。
让我们看看其他问题。给定一个凸双曲余弦函数c,其中c为某些常数,我们可以看到经过几次迭代后,得到 了x = 0处的全局最小值。
c = torch.tensor(0.5)def f(x): # O目标函数return torch.cosh(c * x)def f_grad(x): # 目标函数的梯度return c * torch.sinh(c * x)def f_hess(x): # 目标函数的Hessianreturn c**2 * torch.cosh(c * x)def newton(eta=1):x = 10.0results = [x]for i in range(10):x -= eta * f_grad(x) / f_hess(x)results.append(float(x))print('epoch 10, x:', x)return resultsshow_trace(newton(), f)
现在让我们考虑一个非凸函数,比如f(x) = x cos(cx),c为某些常数。请注意在牛顿法中,我们最终将除 以Hessian。这意味着如果二阶导数是负的,f的值可能会趋于增加。这是这个算法的致命缺陷!让我们看看 实践中会发生什么。
c = torch.tensor(0.15 * np.pi)def f(x):return x * torch.cos(c * x)def f_grad(x):return torch.cos(c * x) - c * x * torch.sin(c * x)def f_hess(x):return - 2 * c * torch.sin(c * x) - x * c ** 2 * torch.cos(c * x)show_trace(newton(), f)
这发生了惊人的错误。我们怎样才能修正它?一种方法是用取Hessian的绝对值来修正,另一个策略是重新引入学习率。这似乎违背了初衷,但不完全是——拥有二阶信息可以使我们在曲率较大时保持谨慎,而在目 标函数较平坦时则采用较大的学习率。让我们看看在学习率稍小的情况下它是如何生效的,比如η = 0.5。如 我们所见,我们有了一个相当高效的算法。
show_trace(newton(0.5), f)
小结:
- 学习率的大小很重要:学习率太大会使模型发散,学习率太小会没有进展。
- 梯度下降会可能陷入局部极小值,而得不到全局最小值。
- 在高维模型中,调整学习率是很复杂的。
- 预处理 有助于调节比例。
- 牛顿法在凸问题中一旦开始正常工作,速度就会快得多。
- 对于非凸问题,不要不作任何调整就使用牛顿法。
1.3 随机梯度下降
在前面的章节中,我们一直在训练过程中使用随机梯度下降,但没有解释它为什么起作用。为了澄清这一点,本节继续更详细地说明 随机梯度下降(stochastic gradient descent)。
%matplotlib inline
import math
import torch
from d2l import torch as d2l在深度学习中,目标函数通常是训练数据集中每个样本的损失函数的平均值。给定n个样本的训练数据集,我们假设fi(x)是关于索引i的训练样本的损失函数,其中x是参数向量。
def f(x1, x2): # 目标函数return x1 ** 2 + 2 * x2 ** 2def f_grad(x1, x2): # 目标函数的梯度return 2 * x1, 4 * x2def sgd(x1, x2, s1, s2, f_grad):g1, g2 = f_grad(x1, x2)# 模拟有噪声的梯度g1 += torch.normal(0.0, 1, (1,)).item()g2 += torch.normal(0.0, 1, (1,)).item()eta_t = eta * lr()return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0)def constant_lr():return 1eta = 0.1
lr = constant_lr # 常数学习速度
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
1.3.1 动态学习率
用与时间相关的学习率η(t)取代η增加了控制优化算法收敛的复杂性。特别是,我们需要弄清η的衰减速度。 如果太快,我们将过早停止优化。如果减少的太慢,我们会在优化上浪费太多时间。
正如预期的那样,参数的方差大大减少。但是,这是以未能收敛到最优解x = (0, 0)为代价的。即使经过1000个,迭代步骤,我们仍然离最优解很远。事实上,该算法根本无法收敛。另一方面,如果我们使用多项式衰减,其中学习率随迭代次数的平方根倒数衰减,那么仅在50次迭代之后,收敛就会更好。
def polynomial_lr():# 在函数外部定义,而在内部更新的全局变量global tt += 1return (1 + 0.1 * t) ** (-0.5)t = 1
lr = polynomial_lr
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
小结:
- 对于凸问题,我们可以证明,对于广泛的学习率选择,随机梯度下降将收敛到最优解。
- 对于深度学习而言,情况通常并非如此。但是,对凸问题的分析使我们能够深入了解如何进行优化,即逐步降低学习率,尽管不是太快。
- 如果学习率太小或太大,就会出现问题。实际上,通常只有经过多次实验后才能找到合适的学习率。
- 当训练数据集中有更多样本时,计算梯度下降的每次迭代的代价更高,因此在这些情况下,首选随机梯度下降。
- 随机梯度下降的最优性保证在非凸情况下一般不可用,因为需要检查的局部最小值的数量可能是指数级的。
二 小批量随机梯度下降
到目前为止,我们在基于梯度的学习方法中遇到了两个极端情况:一是使用完整数据集来计算梯度并更新参数,二是一次处理一个训练样本来取得进展。二者各有利弊:每当数据非常相似时,梯度下降并不是非常“数据高效”。而由于 CPU和GPU无法充分利用向量化,随机梯度下降并不特别“计算高效”。这暗示 了两者之间可能有折中方案,这便涉及到 小批量随机梯度下降(minibatch gradient descent)。
2.1 向量化和缓存
使用 小批量的决策的核心是计算效率。当考虑与多个GPU和多台服务器并行处理时,这一点最容易被理解。 在这种情况下,我们需要向每个GPU发送至少一张图像。有了每台服务器8个GPU和16台服务器,我们 就能得到大小为128的小批量。
当涉及到单个GPU甚至CPU时,事情会更微妙一些:这些设备有多种类型的内存、通常情况下多种类型的计算单元以及在它们之间不同的带宽限制。例如,一个CPU有少量寄存器(register),L1和L2缓存,以及L3缓存(在不同的处理器内核之间共享)。随着缓存的大小的增加,它们的延迟也在增加,同时带宽在减少。可以说,处理器能够执行的操作远比主内存接口所能提供的多得多。
首先,具有16个内核和AVX‐512向量化的2GHz CPU每秒可处理高达2 · 109 · 16 · 32 = 1012个字节。同时,GPU的 性能很容易超过该数字100倍。而另一方面,中端服务器处理器的带宽可能不超过100Gb/s,即不到处理器满负荷所需的十分之一。更糟糕的是,并非所有的内存入口都是相等的:内存接口通常为64位或更宽(例如,在 最多384位的GPU上)。因此读取单个字节会导致由于更宽的存取而产生的代价。
其次,第一次存取的额外开销很大,而按序存取(sequential access)或突发读取(burst read)相对开销较小。
除了计算效率之外,Python和深度学习框架 本身带来的 额外开销 也是相当大的。回想一下,每次我们执行代码时,Python解释器都会向深度学习框架发送一个命令,要求将其插入到计算图中并在调度过程中处理它。 这样的额外开销可能是非常不利的。总而言之,我们最好用 向量化(和矩阵)。
%matplotlib inlineimport numpy as np
import torch
from torch import nn
from d2l import torch as d2ltimer = d2l.Timer()
A = torch.zeros(256, 256)
B = torch.randn(256, 256)
C = torch.randn(256, 256)按元素分配只需遍历分别为B和C的所有行和列,即可将该值分配给A。
timer.start()
for i in range(256):for j in range(256):A[i, j] = torch.dot(B[i, :], C[:, j])timer.stop() # 0.6227602958679199更快的策略是执行按列分配。
# 逐列计算A=BC
timer.start()
for j in range(256):A[:, j] = torch.mv(B, C[:, j])
timer.stop() # 0.01296234130859375最有效的方法是在一个区块中执行整个操作。让我们看看它们各自的操作速度是多少。
# 一次性计算A=BC
timer.start()
A = torch.mm(B, C)
timer.stop()
# 乘法和加法作为单独的操作(在实践中融合)
gigaflops = [2/i for i in timer.times]
print(f'performance in Gigaflops: element {gigaflops[0]:.3f}, 'f'column {gigaflops[1]:.3f}, full {gigaflops[2]:.3f}')# performance in Gigaflops: element 3.212, column 3.670, full 154.2932.2 读取数据集
让我们来看看如何从数据中有效地生成小批量。下面我们 使用NASA开发的测试机翼的数据集不同飞行器产 生的噪声132 来比较这些优化算法。为方便起见,我们只使用前1, 500样本。数据已作预处理:我们移除了均值 并将方差重新缩放到每个坐标为1。
让我们来看看如何从数据中有效地生成小批量。下面我们使用NASA开发的测试机翼的数据集不同飞行器产 生的噪声132来比较这些优化算法。为方便起见,我们只使用前1, 500样本。数据已作预处理:我们移除了均值 并将方差重新缩放到每个坐标为1。
#@save
d2l.DATA_HUB['airfoil'] = (d2l.DATA_URL + 'airfoil_self_noise.dat','76e5be1548fd8222e5074cf0faae75edff8cf93f')
#@save
def get_data_ch11(batch_size=10, n=1500):data = np.genfromtxt(d2l.download('airfoil'),dtype=np.float32, delimiter='\t')data = torch.from_numpy((data - data.mean(axis=0)) / data.std(axis=0))data_iter = d2l.load_array((data[:n, :-1], data[:n, -1]),batch_size, is_train=True)return data_iter, data.shape[1]-12.3 从零开始实现
已经实现过小批量随机梯度下降算法。我们在这里将它的输入参数变得更加通用,主要是为了方 便本章后面介绍的其他优化算法也可以使用同样的输入。具体来说,我们添加了一个状态输入states并将超 参数放在字典hyperparams中。此外,我们将在训练函数里对各个小批量样本的损失求平均,因此优化算法中 的梯度不需要除以批量大小。
def sgd(params, states, hyperparams):for p in params:p.data.sub_(hyperparams['lr'] * p.grad)p.grad.data.zero_()下面实现一个通用的训练函数,以方便本章后面介绍的其他优化算法使用。它初始化了一个线性回归模型, 然后可以使用小批量随机梯度下降以及后续小节介绍的其他算法来训练模型。
#@save
def train_ch11(trainer_fn, states, hyperparams, data_iter,feature_dim, num_epochs=2):# 初始化模型w = torch.normal(mean=0.0, std=0.01, size=(feature_dim, 1),requires_grad=True)b = torch.zeros((1), requires_grad=True)net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss# 训练模型animator = d2l.Animator(xlabel='epoch', ylabel='loss',xlim=[0, num_epochs], ylim=[0.22, 0.35])n, timer = 0, d2l.Timer()for _ in range(num_epochs):for X, y in data_iter:l = loss(net(X), y).mean()l.backward()trainer_fn([w, b], states, hyperparams)n += X.shape[0]if n % 200 == 0:timer.stop()animator.add(n/X.shape[0]/len(data_iter),(d2l.evaluate_loss(net, data_iter, loss),))timer.start()print(f'loss: {animator.Y[0][-1]:.3f}, {timer.avg():.3f} sec/epoch')return timer.cumsum(), animator.Y[0]让我们来看看批量梯度下降的优化是如何进行的。这可以通过将小批量设置为1500(即样本总数)来实现。 因此,模型参数每个迭代轮数只迭代一次。
def train_sgd(lr, batch_size, num_epochs=2):data_iter, feature_dim = get_data_ch11(batch_size)return train_ch11(sgd, None, {'lr': lr}, data_iter, feature_dim, num_epochs)gd_res = train_sgd(1, 1500, 10)
当批量大小为1时,优化使用的是随机梯度下降。为了简化实现,我们选择了很小的学习率。在随机梯度下 降的实验中,每当一个样本被处理,模型参数都会更新。在这个例子中,这相当于每个迭代轮数有1500次更 新。可以看到,目标函数值的下降在1个迭代轮数后就变得较为平缓。尽管两个例子在一个迭代轮数内都处理 了1500个样本,但实验中随机梯度下降的一个迭代轮数耗时更多。这是因为随机梯度下降更频繁地更新了参 数,而且一次处理单个观测值效率较低。
sgd_res = train_sgd(0.005, 1)
mini1_res = train_sgd(.4, 100)
mini2_res = train_sgd(.05, 10)
d2l.set_figsize([6, 3])
d2l.plot(*list(map(list, zip(gd_res, sgd_res, mini1_res, mini2_res))),'time (sec)', 'loss', xlim=[1e-2, 10],legend=['gd', 'sgd', 'batch size=100', 'batch size=10'])d2l.plt.gca().set_xscale('log')
2.4 简洁实现
下面用深度学习框架自带算法实现一个通用的训练函数。
#@save
def train_concise_ch11(trainer_fn, hyperparams, data_iter, num_epochs=4):# 初始化模型net = nn.Sequential(nn.Linear(5, 1))def init_weights(m):if type(m) == nn.Linear:torch.nn.init.normal_(m.weight, std=0.01)net.apply(init_weights)optimizer = trainer_fn(net.parameters(), **hyperparams)loss = nn.MSELoss(reduction='none')animator = d2l.Animator(xlabel='epoch', ylabel='loss',xlim=[0, num_epochs], ylim=[0.22, 0.35])n, timer = 0, d2l.Timer()for _ in range(num_epochs):for X, y in data_iter:optimizer.zero_grad()out = net(X)y = y.reshape(out.shape)l = loss(out, y)l.mean().backward()optimizer.step()n += X.shape[0]if n % 200 == 0:timer.stop()# MSELoss计算平方误差时不带系数1/2animator.add(n/X.shape[0]/len(data_iter),(d2l.evaluate_loss(net, data_iter, loss) / 2,))timer.start()print(f'loss: {animator.Y[0][-1]:.3f}, {timer.avg():.3f} sec/epoch')下面使用这个训练函数,复现之前的实验。
data_iter, _ = get_data_ch11(10)
trainer = torch.optim.SGD
train_concise_ch11(trainer, {'lr': 0.01}, data_iter)小结:
- 由于减少了深度学习框架的额外开销,使用更好的内存定位以及CPU和GPU上的缓存,向量化使代码更加高效。
- 随机梯度下降的“统计效率”与大批量一次处理数据的“计算效率”之间存在权衡。小批量随机梯度下 降提供了两全其美的答案:计算和统计效率。
- 在小批量随机梯度下降中,我们处理通过训练数据的随机排列获得的批量数据(即每个观测值只处理 一次,但按随机顺序)。
- 在训练期间降低学习率有助于训练。
- 一般来说,小批量随机梯度下降比随机梯度下降和梯度下降的速度快,收敛风险较小。
相关文章:

深度学习中的优化算法二(Pytorch 19)
一 梯度下降 尽管梯度下降(gradient descent)很少直接用于深度学习,但了解它是理解下一节 随机梯度下降算法 的关键。例如,由于学习率过大,优化问题可能会发散,这种现象早已在梯度下降中出现。同样地&…...

R实验 方差分析
实验目的: 掌握单因素方差分析的思想和方法; 掌握多重均值检验方法; 掌握多个总体的方差齐性检验; 掌握Kruskal-Wallis秩和检验的思想和方法; 掌握多重Wilcoxon秩和检验的思想和方法。 实验内容: &…...

AI智能体|手把手教你使用扣子Coze图像流的文生图功能
大家好,我是无界生长。 AI智能体|手把手教你使用扣子Coze图像流的文生图功能本文详细介绍了Coze平台的\x26quot;图像流\x26quot;功能中的\x26quot;文生图\x26quot;节点,包括创建图像流、编排文生图节点、节点参数配置,并通过案例…...

应用程序图标提取
文章目录 [toc]提取过程提取案例——提取7-zip应用程序的图标 提取过程 找到需要提取图标的应用程序的.exe文件 复制.exe文件到桌面,并将复制的.exe文件后缀改为.zip 使用解压工具7-zip解压.zip文件 在解压后的文件夹中,在.rsrc/ICON路径下的.ico文件…...

Excel表格在线解密:轻松解密密码,快速恢复数据
忘记了excel表格密码?教你简单两步走:具体步骤如下。首先,在百度搜索中键入“密码帝官网”。其次,点击“立即开始”,在用户中心上传表格文件即可找回密码。这种方法不用下载软件,操作简单易行,适…...
springboot小结1
什么是springboot Spring Boot是为了简化Spring应用的创建、运行、调试、部署等而出现的,使用它可以做到专注于Spring应用的开发,而无需过多关注XML的配置。 简单来说,它提供了一堆依赖打包Starter,并已经按照使用习惯解决…...

【Qt 学习笔记】Qt窗口 | 菜单栏 | QMenuBar的使用及说明
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt窗口 | 菜单栏 | QMenuBar的使用及说明 文章编号:Qt 学习…...

Spark运行模式详解
Spark概述 Spark 可以在多种不同的运行模式下执行,每种模式都有其自身的特点和适用场景。 部署Spark集群大体上分为两种模式:单机模式与集群模式。大多数分布式框架都支持单机模式,方便开发者调试框架的运行环境。但是在生产环境中ÿ…...

vcpkg环境配置
vcpkg 使用linux相关库,设置环境变量VCPKG_ROOT,设置cmake工具链$VCPKG_ROOT/scripts\buildsystems\vcpkg.cmake set VCPKG_DEFAULT_TRIPLETx64-windows .\vcpkg.exe install fftw3 freetype gettext glibmm gtkmm libjpeg-turbo libpng libxmlpp libs…...

python学习:基础语句
目录 条件语句 循环语句 for 循环 while 循环 break continue 条件语句 Python提供了 if、elif、else 来进行逻辑判断。格式如下: Pythonif 判断条件1: 执行语句1... elif 判断条件2: 执行语句2... elif 判断条件3: 执行语句3... else: 执行语句4…...

Nginx限制IP访问详解
在Web服务器管理中,限制某些IP地址访问网站是一个常见的需求。Nginx作为一款高性能的HTTP服务器和反向代理服务器,提供了灵活强大的配置选项来实现这一功能。本文将详细讲解如何在Nginx中限制IP访问,并通过示例代码展示具体操作。 一、Nginx…...

Three.js——二维平面、二维圆、自定义二维图形、立方体、球体、圆柱体、圆环、扭结、多面体、文字
个人简介 👀个人主页: 前端杂货铺 ⚡开源项目: rich-vue3 (基于 Vue3 TS Pinia Element Plus Spring全家桶 MySQL) 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 …...

24年湖南教资认定即将开始,别被照片卡审!
24年湖南教资认定即将开始,别被照片卡审!...

数据库(8)——DML数据操作
增添数据 给指定字段添加数据 INSERT INTO 表名 (字段名1,字段名2,...)VALUES(值1,值2...); 没有的添加的字段默认为NULL。 给全部字段添加数据 INSERT INTO 表名 VALUE (值1,值2,....值n); 此时值的顺序对应表中字段的顺序 批量添加数据 INSERT INTO 表名(字段1,…...

Gitee在已有项目基础上创建仓库中遇到的问题和解决
问题一:fatal: remote origin already exists 解释:当前仓库添加了一个名为"origin"的远程仓库配置,此时输入 git remote add origin https://xxx就会提示上面的内容。 解决方案1:移除旧的origin git remote remove origin 解决方案…...

【推荐算法-特征工程】每种item单侧特征,都可产生对应user单侧特征
比如item的平均成单价格,可以分成10个档位,作为一个标签值打在item上, 那么对应user对item的click用户行为,就能产生user-click的10个档位作为特征值 作为user的标签。 比如item的平均点击率,也可以分成比如20个档位…...
一行代码实现UI拖拽的效果
演示 先来看效果吧! 实现方式 1.首先创建一个你想拖动的UI图片 2.创建一个C#的脚本 3.编写控制脚本(代码按我的敲就行) 付上代码片段 public void OnDrag(PointerEventData eventData){transform.position eventData.position;} 4.添加脚…...
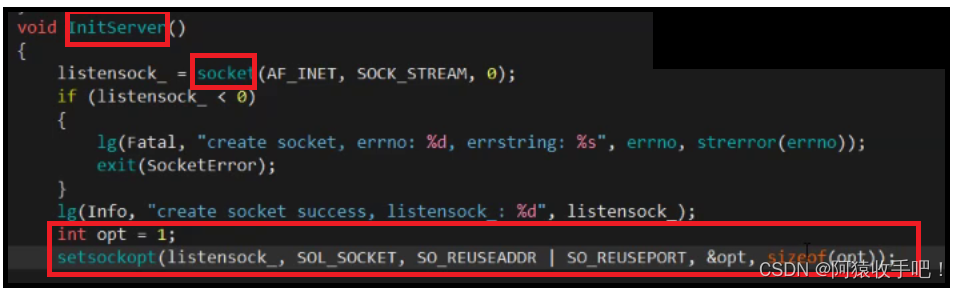
【Linux】TCP协议【下一】{三次握手/四次挥手的深度解读==状态变化}
文章目录 本篇知识需要有TCP协议【中】的知识!详情点击👇1.测试一:服务器start函数不定义任何行为(不调用accept)的三次握手状态变化int listen(int sockfd, int backlog);的backlog参数全连接队列当全连接队列已满&am…...

【C语言回顾】编译和链接
前言1. 编译2. 链接结语 上期回顾: 【C语言回顾】文件操作 个人主页:C_GUIQU 归属专栏:【C语言学习】 前言 各位小伙伴大家好!上期小编给大家讲解了C语言中的文件操作,接下来我们讲解一下编译和链接! 1. 编译 预处理…...

2024年5月27日 十二生肖 今日运势
小运播报:2024年5月27日,星期一,农历四月二十 (甲辰年己巳月辛卯日),法定工作日。 红榜生肖:羊、蛇、狗 需要注意:鼠、鸡、龙 喜神方位:西南方 财神方位:…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
