自定义类型:结构体详解
1.结构体
1.1 结构的基础知识
结构是一些值的集合,这些值称为成员变量。一个整型数组,它的每个数组元素只能是整型,字符型的数组它的每个元素只能是字符型。但是结构体的每个成员可以是各种不同类型的变量。
1.2结构的声明
//声明
struct tag
{member - list;
}variable-list;
//比如要描述一个学生的信息
struct Stu
{char name[20];int age;char sex[5];char id[20];
};
1.3 特殊的声明
在声明结构体的时候,可以不完全的声明
//这就是匿名结构体类型
struct
{int a;char b;float c;
}x;struct
{int a;char b;float c;
}a[20],*p;
顾名思义,匿名,就是结构体在声明的时候省略掉了结构体标签(tag)。
那么我们可以思考一下这个问题
//在上面代码的基础上,下面的代码合法吗?
p=&x;
这种写法是不可以的,编译器会把上面的两个声明当成完全不同的两个类型,所以是非法的。
1.4 结构体的自引用
在数据结构中,有顺序访问和链式访问两种数据的访问方式:
顺序访问,就是按照顺序,一个接一个访问
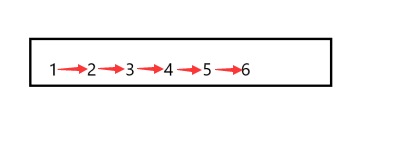
链式访问主要针对数据没有在一块连续的空间,而是分散在各个内存块上的情况,这样前一个数要想顺利找到下一个数据,就必须在存储自身数据的同时还存储了下一个数据的地址,这样就能顺着地址成功找到下一个数据:
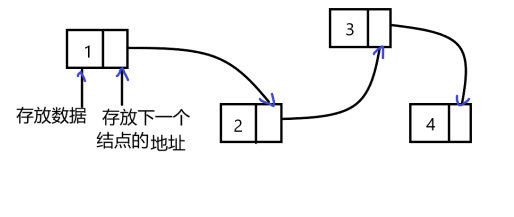
那么我们如果用结构体这么来实现是否可行:
struct Node
{int data;struct Node next;
};
答案是不可以,因为我们没有办法计算sizeof(struct Node)。
正确的自引用方式应该是这样:
struct Node
{int data;struct Node* next;
};
1.5 结构体变量的定义和初始化
结构体变量的定义有两种方式:
struct S
{int a;char b;float c;
}s1;//声明类型的同时定义变量s1 struct S s2;//定义结构体变量s2
结构体变量的初始化
//第一种初始化方法
struct S
{int a;char b;float c;
}s1 = { 20,'c',3.14 }, s2 = {.c=5.2,.b='a',.a=10};//这种初始化的方法可以打破顺序的限制//第二种初始化方法
struct S s3 = { 30,'d',6.0 };
1.6 结构体内存对齐
如何计算一个结构体的大小呢?
首先得掌握结构体的对齐规则:
1.结构体的第一个成员永远放在相较于起始位置偏移量为0的位置。
2.从第二个成员开始,往后的每个成员都要对齐到某个对齐数的整数倍处,对齐数就是结构体成员自身的大小和默认对齐数的较小值,VS的默认对齐数是8。
(gcc没有默认对齐数,对齐数就是结构体成员的自身大小。)
3.结构体的总大小,必须是最大对齐数的整数倍,最大对齐数是所有成员对齐数中最大的值。
举个例子吧:
struct S
{char a;int b;char c;
};
int main()
{printf("%d", sizeof(struct S));//大小是12return 0;
}

为什么会存在内存对齐呢?
1.平台原因
不是所有的硬件平台都能访问任意地址上的任意数据的,某些硬件平台只能在某些地址处取某些特定类型的数据,否则会抛出硬件异常。
2.性能原因
数据结构(尤其是栈)应该尽可能地在自然边界上对齐。
原因在于,为了访问未对其的内存,处理器需要作两次内存访问,而对齐的内存访问仅需要一次访问。
总体来说,结构体的内存对齐是拿空间来换取时间的做法。所以在设计结构体的时候,我们既要满足对齐,又要节省空间,就需要让一些占用空间小的成员尽量集中在一起,例如
struct S
{char a;char c;int b;
};
1.7 修改默认对齐数
默认对齐数是可以修改的,我们可以用#pragma来修改:
#pragma pack(8)//修改默认对齐数是8
struct S
{char a;char c;int b;
};
#pragma pack()//取消设置的默认对齐数,还原为默认
所以在结构对齐方式不合适的时候,我们可以自己设置默认对齐数
相关文章:

自定义类型:结构体详解
1.结构体 1.1 结构的基础知识 结构是一些值的集合,这些值称为成员变量。一个整型数组,它的每个数组元素只能是整型,字符型的数组它的每个元素只能是字符型。但是结构体的每个成员可以是各种不同类型的变量。 1.2结构的声明 //声明 struct t…...

嵌入式进阶——舵机控制PWM
🎬 秋野酱:《个人主页》 🔥 个人专栏:《Java专栏》《Python专栏》 ⛺️心若有所向往,何惧道阻且长 文章目录 舵机信号线代码示例初始化PWM初始化UART打印日志初始化外部中断Extimain函数 舵机最早用于船舶上实现转向功能,由于可以通过程序连…...

Java实现抢红包算法——详细注释,标准语法
package learn;import java.math.BigDecimal; import java.util.ArrayList; import java.util.List; import java.util.Random;public class RobRedPacket {// 发红包算法,金额参数以分为单位public static List<Integer> divideRedPacket(Integer totalAmoun…...
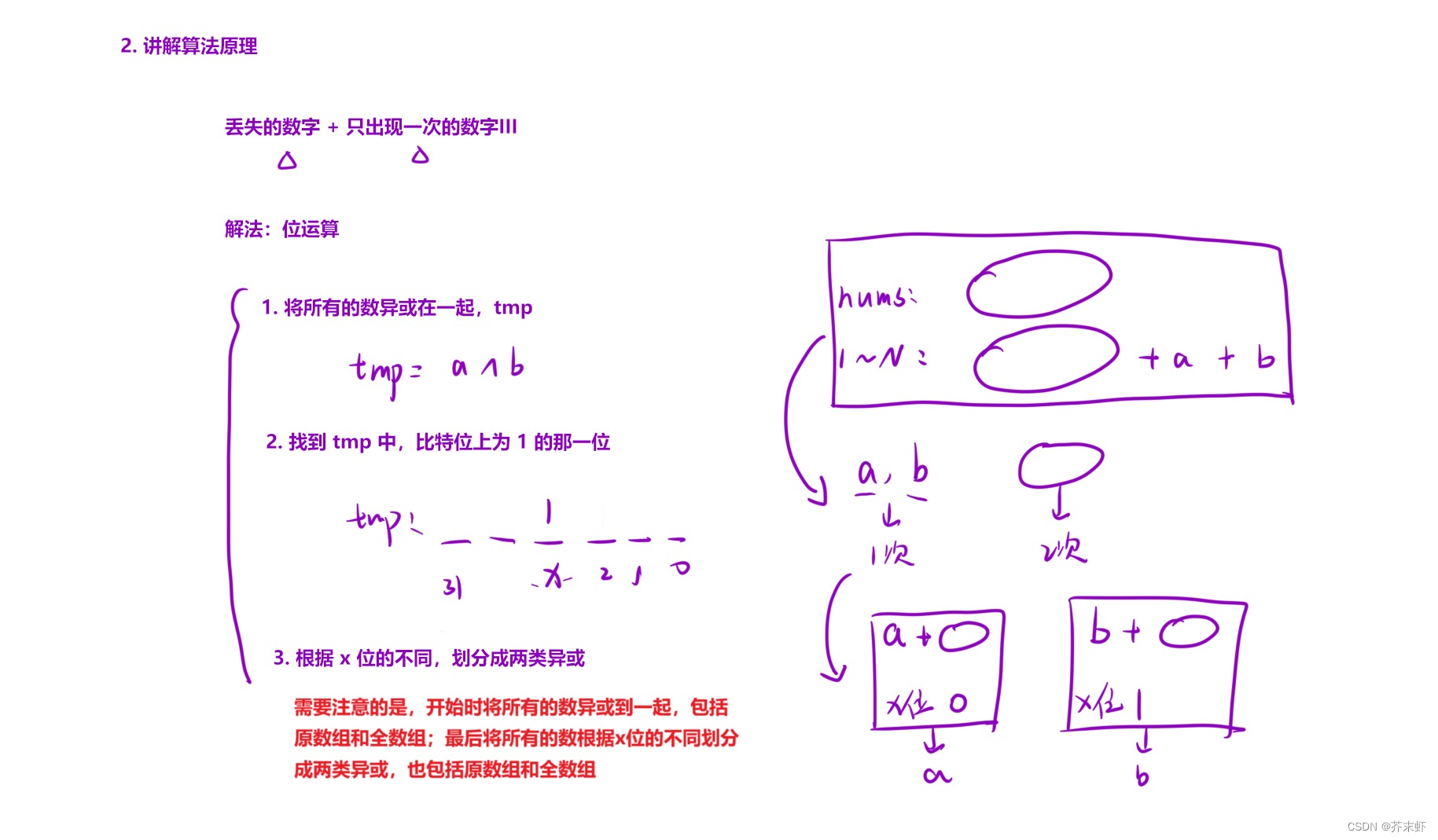
【优选算法】位运算 {位运算符及其优先级;位运算的应用:判断位,打开位,关闭位,转置位,位图,get lowbit,close lowbit;相关编程题解析}
一、位运算符及其优先级 我们知道,计算机中的数在内存中都是以二进制形式进行存储的 ,而位运算就是直接对整数在内存中的二进制位进行操作,因此其执行效率非常高,在程序中尽量使用位运算进行操作,这会大大提高程序的性…...

服务器数据恢复—服务器正常断电重启后raid信息丢失的数据恢复案例
服务器数据恢复环境: 一台某品牌DL380 G4服务器,服务器通过该服务器品牌smart array控制器挂载了一台国产的磁盘阵列,磁盘阵列中有一组由14块SCSI硬盘组建的RAID5。服务器安装LINUX操作系统,搭建了NFSFTP,作为内部文件…...

如何理解kmp的套娃式算法啊?
概念 KMP算法,全称Knuth Morris Pratt算法 。文章大部分内容出自《数据结构与算法之美》 核心思想 假设主串是a,模式串是b 在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,对已经对比过的字符,是否能找到…...

python中树的运用样例
目录 一、文件系统样例 二、Trie树 一、文件系统样例 class FileNode:def __init__(self, name, is_fileFalse):self.name nameself.is_file is_fileself.children []def add_child(self, child):self.children.append(child)# 创建文件系统结构 root FileNode("roo…...

C++学习/复习5--构造函数与初始化/static成员/友元/内部类/匿名对象/编译器的拷贝构造优化
一、本章概要 二、再谈构造函数 1.构造体赋初值与初始化 2.初始化列表与初始化 2.1定义 2.2注意事项与举例 3.explicit关键字与构造函数 3.1隐式类型转换 也叫做自动类型转换 这种转换通常是从存储范围小的类型到存储范围大的类型,或者是从低精度的数值类型到高…...

数学建模--LaTeX基本介绍和入门
1.引言 (1)上次我们介绍到了我们这个团队第一次参加这个数学建模比赛,就是这个电工杯,我是一名论文手,我们在这个下午也是对于这个比赛过程中出现的问题做了相应的分析,每个人也是进行了反思,知…...

【Java面试】二、Redis篇(中)
文章目录 1、Redis持久化1.1 RDB1.2 AOF1.3 RDB与AOF的对比 2、数据过期策略(删除策略)2.1 惰性删除2.2 定期删除 3、数据淘汰策略4、主从复制4.1 主从全量同步4.2 增量同步 5、哨兵模式5.1 服务状态监控5.2 哨兵选主规则5.3 哨兵模式下,Redi…...
v1.30.1)
二进制安装Kubernetes(k8s)v1.30.1
二进制安装Kubernetes(k8s)v1.30.1 https://github.com/cby-chen/Kubernetes 开源不易,帮忙点个star,谢谢了 介绍 kubernetes(k8s)二进制高可用安装部署,支持IPv4IPv6双栈。 我使用IPV6的目的是…...
俄罗斯半导体领域迈出坚实步伐:首台光刻机诞生,目标直指7纳米工艺
近日,国外媒体纷纷报道,俄罗斯在半导体技术领域取得了重要突破,首台光刻机已经制造完成并正在进行严格的测试阶段。这一里程碑式的事件标志着俄罗斯在自主发展半导体技术的道路上迈出了坚实的一步。 据俄罗斯联邦工业和贸易部副部长瓦西里-什…...

什么是容器:从基础到进阶的全面介绍
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

力扣 第 399 场周赛 解题报告 | 珂学家 | 调和级数 + 分块DP
前言 T1. 优质数对的总数 I 题型: 签到 class Solution:def numberOfPairs(self, nums1: List[int], nums2: List[int], k: int) -> int:res 0for v1 in nums1:for v2 in nums2:if v1 % (v2 * k) 0:res 1return resT2. 压缩字符串 III 思路: 模拟 感觉引入一个栈&…...
Redis的下载、安装、启动和初尝试【超级简单】
redis最好是在Linux系统中使用,这是最接近生产实际的环境。 不过,我们初学者,目的是学习Redis的使用、原理,如果在Linux下直接学习Redis,很可能会因为命令不熟悉而劝退,这是不好的。 因此,我主张…...
v-cloak 用于在 Vue 实例渲染完成之前隐藏绑定的元素
如果你是后端开发者(php),在接触一些vue2开发的后台时,会发现有这段代码: # CDN <script src"https://cdn.jsdelivr.net/npm/vue2/dist/vue.js"></script> # 或 <script src"https://cd…...

港股:并不意外的获利了结
中金公司表示,风险偏好驱动的反弹已经较为充分,分歧和获利了结也不意外。接下来或在当前水平震荡盘整,等待更多催化剂。 在持续一个月的大涨后,港股市场上周出现明显回调。此前我们多次提示,市场已经超买,情…...
)
Python项目开发实战:工厂库存管理系统(案例教程)
一、项目背景与意义 随着制造业的快速发展,工厂库存管理成为了企业运营中不可或缺的一部分。一个高效的库存管理系统能够确保物料供应的及时性、降低库存成本、提高生产效率。因此,我们决定使用Python开发一个工厂库存管理系统,以满足工厂日常库存管理的需求。 二、系统需求…...

VS2022 嘿嘿
还是大二的时候就开始用这个,但居然是为了用PB,-_-|| 用了段时间换成了C#,依稀还记得大佬们纠正我的读法,别读C井,应该读C夏普。。。 安装过程其实也没啥,就是关键Key得花时间找,我好不容易搞…...

Flutter 中的 PhysicalShape 小部件:全面指南
Flutter 中的 PhysicalShape 小部件:全面指南 在Flutter中,PhysicalShape小部件是一个能够为子组件添加物理效果的边框和阴影的装饰性小部件。它能够模拟真实世界中物体的立体感,通过在子组件的周围创建一个可自定义的形状,并添加…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
