【机器学习】——线性模型
💻博主现有专栏:
C51单片机(STC89C516),c语言,c++,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux,基于HTML5的网页设计及应用,Rust(官方文档重点总结),jQuery,前端vue.js,Javaweb开发,Python机器学习等
🥏主页链接:Y小夜-CSDN博客
目录
🎯本文目的
🎯单变量线性回归预测披萨价格
🎃内容
🎃代码解析
🎃可能会发生的错误
✨测试数据无法测试进行reshape
✨不知道如何在图上显示测试后的数据
🎯二元线性模型预测学生成绩
🎃内容
🎃代码解析
🎯岭回归预测波士顿房价
🎃内容
🎃代码解析
🎯套索回归预测波士顿房价
🎃内容
🎃代码解析
🎯逻辑回归识别鸢尾花
🎃内容
🎃代码解析
🎃可能会发生的错误
✨逻辑回归模型最大迭代次数没有收敛
✨不知道如何调整逻辑回归模型的参数
🎯本文目的
- (一)理解线性模型的基本原理
- (二)能够使用pandas生成简单数据集
- (三)能够使用sklearn库进行线性模型的训练和预测
- (四)掌握岭回归、套索回归模型的参数调节
- (五)能够使用sklearn库进行逻辑回归模型的训练和预测
🎯单变量线性回归预测披萨价格
🎃内容
披萨价格和披萨的直径关系如下表所示。
直径(英寸)
价格(美元)
6
7
8
11
10
13
14
17.5
18
18
要求:
- 使用一元线性回归模型
- 输出模型的参数。
- 预测直径为12英寸的披萨价格是多少?
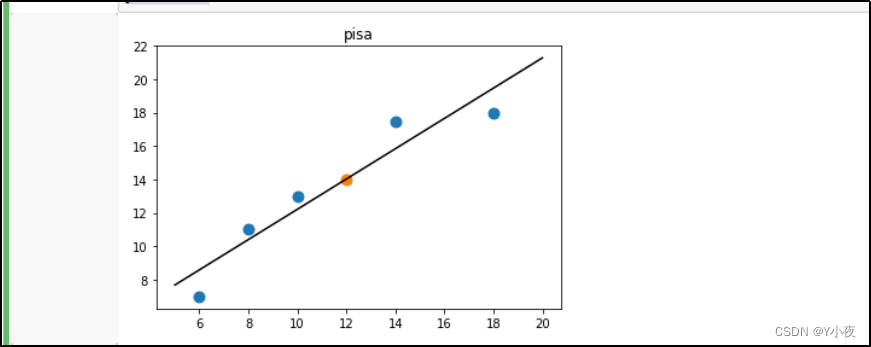
- 图形展示样本数据及模型。(使用直线图形展示模型,使用散点图展示各个数据点)
🎃代码解析
import pandas as pddata={'foot':[6,8,10,14,18],'price':[7,11,13,17.5,18]}data_frame=pd.DataFrame(data)data_frame.head()
使用了Pandas 库创建了一个数据框(DataFrame),其中包含了两列数据:
foot和price。foot列包含了脚的尺寸数据,而price列包含了对应的鞋子价格数据。接下来,data_frame.head()方法被调用,该方法用于显示数据框的前几行,默认显示前五行。这是为了让用户能够快速浏览数据框的内容。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegressionreg=LinearRegression()x=data_frame['foot'].values.reshape(-1,1)y=data_frame['price']reg.fit(x,y)使用了 NumPy、Matplotlib 和 Scikit-learn 库。首先,它从
data_frame数据框中提取了foot列和price列的数据作为自变量x和因变量y。然后,使用 Scikit-learn 中的线性回归模型(LinearRegression)对数据进行拟合,即通过最小化残差平方和来拟合线性模型的系数。
print(reg.coef_,reg.intercept_)
这段代码打印了线性回归模型的系数和截距。在线性回归模型中,系数表示自变量的变化对因变量的影响,截距表示当自变量为0时,因变量的值。
pisa=np.array([12]).reshape(-1,1)reg.predict(pisa)
这段代码使用了训练好的线性回归模型
reg对输入的pisa数据进行了预测。在这里,pisa是一个 NumPy 数组,包含了一个值为 12 的数据点,通过.reshape(-1,1)将其转换成了二维数组的形式,以满足线性回归模型的输入要求。
z=np.linspace(5,20,20) plt.scatter(x,y,s=80) plt.scatter([12],reg.predict(pisa),s=80) plt.plot(z,reg.predict(z.reshape(-1,1)),c='k') plt.title('pisa') plt.show()
这段代码绘制了一个散点图,并在其中添加了线性回归模型的拟合线和一个新数据点的预测结果。
plt.scatter(x, y, s=80)绘制了原始数据的散点图,其中x是脚的尺寸,y是对应的鞋子价格。参数s控制了散点的大小。
plt.scatter([12], reg.predict(pisa), s=80)添加了一个新数据点(12, 预测值)的散点,其中预测值通过模型对尺寸为 12 的脚进行预测得到。
plt.plot(z, reg.predict(z.reshape(-1,1)), c='k')绘制了线性回归模型的拟合线,其中z是从 5 到 20 的一系列数值,表示了脚的尺寸范围。
z是一个包含了一系列脚的尺寸的数组,范围从 5 到 20,这些数值用来表示横坐标的取值范围。
reg.predict(z.reshape(-1,1))使用训练好的线性回归模型reg对输入的尺寸数据进行预测,得到对应的价格预测值。
plt.plot(z, reg.predict(z.reshape(-1,1)), c='k')绘制了这些尺寸数据与对应的价格预测值之间的关系。参数c='k'设置了线条的颜色为黑色。
plt.title('pisa')设置了图表的标题为 'pisa'。
plt.show()显示了绘制好的图表。
🎃可能会发生的错误
✨测试数据无法测试进行reshape
问题描述:
原因:
当尝试使用
reg.predict(pisa)进行预测时出现了错误。错误信息指出输入的数据需要是一个二维数组,但你提供了一个一维数组。为了解决这个问题,你可以按照提示使用reshape(-1, 1)方法将数据转换成二维数组的形式,或者直接将其作为包含单个样本的二维数组。解决办法:
pisa=np.array([12]).reshape(-1,1) reg.predict(pisa)
✨不知道如何在图上显示测试后的数据
问题描述:
没有x=12的那个点
原因:
没有scatter()中生成
解决办法:
在描述其他点后,在加入这个点(添加一下代码),最后在画图
plt.scatter([12],reg.predict(pisa),s=80)
🎯二元线性模型预测学生成绩
🎃内容
学生的最终成绩由平时成绩和期末成绩构成。某课程的成绩构成标准未知。有7个学生的数据样本如下图所示。某位同学平时成绩83,期末成绩85,预测该同学的最终成绩是多少?
🎃代码解析
import pandas as pd data={'pingshi':[80,82,85,90,86,82,78],'qimo':[86,80,78,90,82,90,80],'zuizhong':[84.2,80.6,80.1,90,83.2,87.6,79.4]} data_frame=pd.DataFrame(data) data_frame.head(7)
创建了一个包含学生考试成绩的DataFrame,其中包括平时成绩(pingshi)、期末考试成绩(qimo)和最终总成绩(zuizhong)。数据包含了7个学生的成绩信息。
- 平时成绩列包含了每个学生的平时考试成绩。
- 期末考试成绩列包含了每个学生的期末考试成绩。
- 最终总成绩列包含了每个学生的最终总成绩,这可能是平时成绩和期末考试成绩的加权平均值或者其他组合方式计算得出。
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression reg=LinearRegression() x=data_frame.drop('zuizhong',axis=1) y=data['zuizhong'] reg.fit(x,y)
使用了Scikit-Learn库中的LinearRegression模型对学生的平时成绩(pingshi)和期末考试成绩(qimo)来预测最终总成绩(zuizhong)。
具体步骤如下:
- 从DataFrame中提取特征x,这里是平时成绩和期末考试成绩,即去除了最终总成绩这一列。
- 从数据字典中提取目标变量y,即最终总成绩。
- 初始化一个LinearRegression模型reg。
- 使用提取的特征x和目标变量y来拟合(训练)LinearRegression模型。
- 训练后,模型将会得出最佳拟合的系数和截距,用于预测最终总成绩。
student=[[83,85]] reg.predict(student)
用训练好的线性回归模型
reg对一个新的学生的平时成绩和期末考试成绩进行预测。这个新的学生的平时成绩为83,期末考试成绩为85。具体步骤如下:
- 创建一个包含平时成绩和期末考试成绩的二维列表
student,其中平时成绩为83,期末考试成绩为85。- 调用
reg.predict(student)方法,使用训练好的模型对这个学生的成绩进行预测。
print(reg.coef_,reg.intercept_) print(f"所以该课程成绩构成标准为:最终成绩= {reg.coef_[0]}*平时成绩 + {reg.coef_[1]}*期末成绩 + {reg.intercept_}")
打印了线性回归模型的系数(coefficients)和截距(intercept),然后使用这些参数构建了最终的成绩构成标准。
具体解析如下:
reg.coef_是一个数组,包含了线性回归模型中每个特征(平时成绩和期末考试成绩)的系数。reg.intercept_是截距,表示当所有特征都为0时,最终总成绩的预测值。
🎯岭回归预测波士顿房价
🎃内容
使用岭回归预测波士顿房价,并调试参数拟合出一个合适的模型。提示:波士顿房价数据集在datasets.load_boston中。
🎃代码解析
from sklearn.datasets import load_boston data1=load_boston() from sklearn.model_selection import train_test_split x,y=data1.data,data1.target x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=8) x.shape,x_train.shapefrom sklearn.linear_model import Ridge ridge=Ridge(alpha=200000).fit(x_train,y_train) print(ridge.score(x_train,y_train)) print(ridge.score(x_test,y_test))
使用了波士顿房价数据集(Boston House Prices dataset)进行岭回归(Ridge Regression)的建模和评估。
具体步骤如下:
导入波士顿房价数据集并分割数据集为训练集和测试集:
- 使用
load_boston()函数加载波士顿房价数据集,数据集包括房屋特征(x)和目标变量(y)。- 使用
train_test_split函数将数据集分割为训练集(x_train和y_train)和测试集(x_test和y_test),设置了random_state=8来确保随机性的可重复性。建立岭回归模型并进行训练:
- 使用
Ridge类创建岭回归模型ridge,设置了alpha=200000作为正则化参数。- 使用训练集数据(
x_train和y_train)对岭回归模型进行训练。输出模型在训练集和测试集上的决定系数(R²分数):
- 使用
score方法分别计算并输出岭回归模型在训练集和测试集上的决定系数(R²分数),用于评估模型的拟合程度。
🎯套索回归预测波士顿房价
🎃内容
使用套索回归预测波士顿房价,并调试参数拟合出一个合适的模型。提示:波士顿房价数据集在datasets.load_boston中。
🎃代码解析
from sklearn.datasets import load_boston data1=load_boston() from sklearn.model_selection import train_test_split x,y=data1.data,data1.target x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=8) x.shape,x_train.shape from sklearn.linear_model import Lasso ridge=Lasso(alpha=20).fit(x_train,y_train) print(ridge.score(x_train,y_train)) print(ridge.score(x_test,y_test))
这段代码与上一个类似,但是使用的是Lasso回归(Lasso Regression)而不是岭回归。
具体步骤如下:
导入波士顿房价数据集并分割数据集为训练集和测试集,与之前相同。
建立Lasso回归模型并进行训练:
- 使用
Lasso类创建Lasso回归模型ridge,设置了alpha=20作为正则化参数。- 使用训练集数据(
x_train和y_train)对Lasso回归模型进行训练。输出模型在训练集和测试集上的决定系数(R²分数):
- 使用
score方法分别计算并输出Lasso回归模型在训练集和测试集上的决定系数(R²分数),用于评估模型的拟合程度。
🎯逻辑回归识别鸢尾花
🎃内容
请使用逻辑回归识别鸢尾花,并调试参数拟合出一个合适的模型。
提示:鸢尾花数据集在datasets.load_iris中。
🎃代码解析
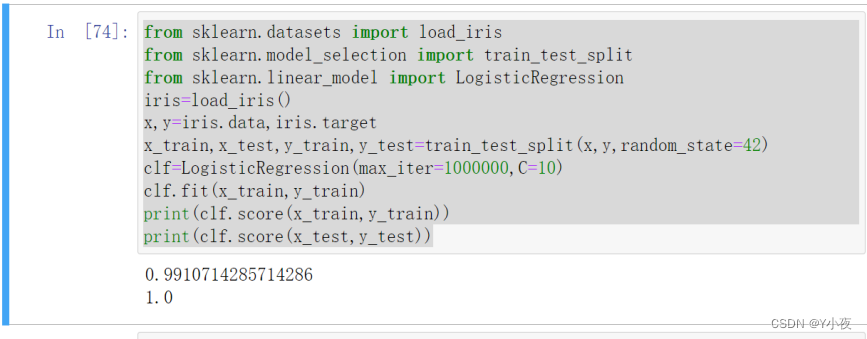
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression iris=load_iris() x,y=iris.data,iris.target x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=42) clf=LogisticRegression(max_iter=1000000,C=10) clf.fit(x_train,y_train) print(clf.score(x_train,y_train)) print(clf.score(x_test,y_test))
使用了鸢尾花数据集(Iris dataset)进行逻辑回归(Logistic Regression)的建模和评估。
具体步骤如下:
导入鸢尾花数据集并分割数据集为训练集和测试集:
- 使用
load_iris()函数加载鸢尾花数据集,数据集包括花朵的特征(x)和类别标签(y)。- 使用
train_test_split函数将数据集分割为训练集(x_train和y_train)和测试集(x_test和y_test),设置了random_state=42来确保随机性的可重复性。建立逻辑回归模型并进行训练:
- 使用
LogisticRegression类创建逻辑回归模型clf,设置了max_iter=1000000来增加最大迭代次数,C=10作为正则化参数。- 使用训练集数据(
x_train和y_train)对逻辑回归模型进行训练。输出模型在训练集和测试集上的准确率(Accuracy):
- 使用
score方法分别计算并输出逻辑回归模型在训练集和测试集上的准确率,用于评估模型的性能。
🎃可能会发生的错误
✨逻辑回归模型最大迭代次数没有收敛
问题描述:
原因:
这个警告是由于逻辑回归模型在默认的最大迭代次数下没有收敛而产生的。你可以尝试增加
max_iter参数的值来解决这个问题。解决办法:
clf=LogisticRegression(max_iter=1000000,C=10)
✨不知道如何调整逻辑回归模型的参数
问题描述:
逻辑回归模型过拟合或者欠拟合时,不知道如何调整参数
解决办法:
在Scikit-learn中,逻辑回归模型(LogisticRegression)不具有
alpha参数。alpha通常用于控制正则化的强度,但在逻辑回归模型中,正则化是通过penalty参数来控制的,默认情况下为L2正则化。如果你想要使用L2正则化并且调整正则化强度,可以修改
C参数,其中C是正则化的倒数,因此较小的C值表示更强的正则化。如:
clf = LogisticRegression(max_iter=1000, C=0.1)
相关文章:
【机器学习】——线性模型
💻博主现有专栏: C51单片机(STC89C516),c语言,c,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux…...

最全的Redis常用命令
Redis是一个开源的内存数据结构存储系统,用作数据库、缓存和消息代理。它支持多种类型的数据结构,如字符串(strings)、哈希(hashes)、列表(lists)、集合(sets)…...
sourcetree推送到git上面
官网:Sourcetree | Free Git GUI for Mac and Windows 下载到1次提交 下载后打开 点击跳过 下一步 名字邮箱 点击clone 把自己要上传的代码粘贴到里面去 返回点击远程->点击暂存所有 加载完毕后,输入提交内容提交 提交完成了 2次提交 把文件夹内的…...

勒索病毒的策略与建议
随着网络技术的快速发展,勒索病毒攻击成为全球范围内日益严重的网络安全威胁。勒索病毒通过加密用户文件或锁定系统来勒索赎金,给个人和企业带来了巨大的损失。因此,了解如何应对勒索病毒攻击至关重要。本文将概述一些有效的防范措施和应对策…...
——输出格式)
doxygen 1.11.0 使用详解(十四)——输出格式
目录 HTMLLATEXMan pagesRTFXMLDocBookCompiled HTML Help (a.k.a. Windows 98 help)Qt Compressed Help (.qch)Eclipse HelpXCode DocSetsPostScriptPDF The following output formats are directly supported by doxygen: HTML Generated if GENERATE_HTML is set to YES i…...

java list<AnalystEducationDO> 转成List<AnalystEducationRespVO>两个对象的属性一样
如果AnalystEducationDO和AnalystEducationRespVO两个类的属性完全相同,且遵循Java Bean的命名规范(即具有相应的getter和setter方法),你可以利用一些库来简化转换过程,比如Apache BeanUtils或Spring Framework的BeanU…...
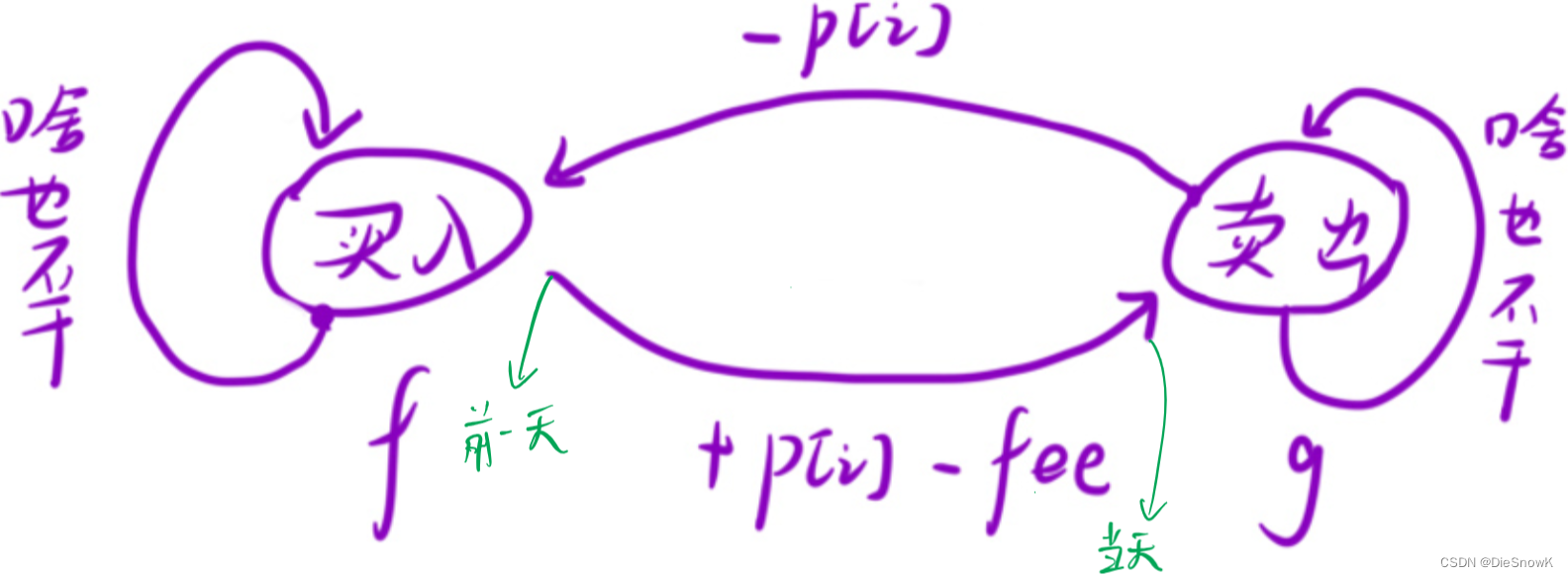
[Algorihm][简单多状态DP问题][买卖股票的最佳时机含冷冻期][买卖股票的最佳时机含手续费]详细讲解
目录 1.买卖股票的最佳时机含冷冻期1.题目链接买卖股票的最佳时机含冷冻期2.算法原理详解3.代码实现 2.买卖股票的最佳时机含手续费1.题目链接2.算法原理详解3.代码实现 1.买卖股票的最佳时机含冷冻期 1.题目链接 买卖股票的最佳时机含冷冻期 2.算法原理详解 思路ÿ…...
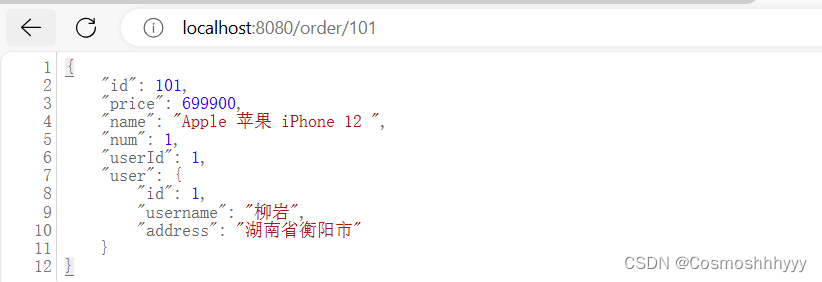
微服务:利用RestTemplate实现远程调用
打算系统学习一下微服务知识,从今天开始记录。 远程调用 调用order接口,查询。 由于实现还未封装用户信息,所以为null。 下面我们来使用远程调用用户服务的接口,然后封装一下用户信息返回即可。 流程图 配置类中注入RestTe…...
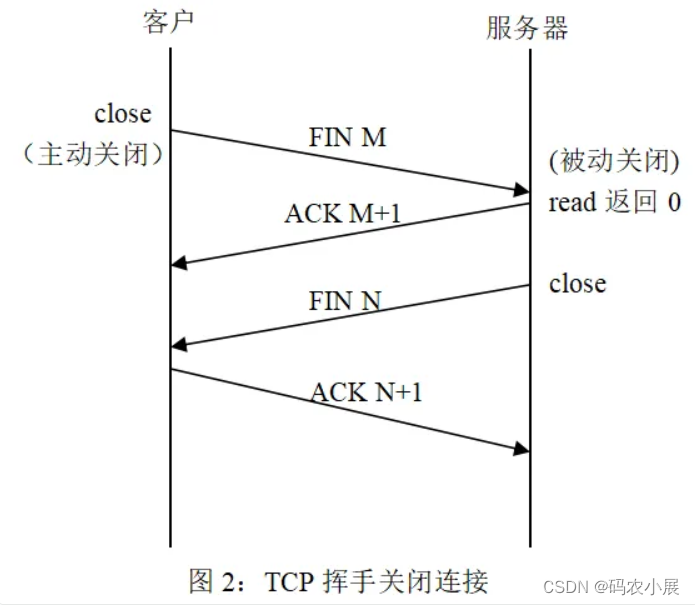
【Linux】TCP的三次握手和四次挥手
三次握手 在TCP/IP协议中,TCP协议提供可靠的连接服务,采用三次握手建立一个连接。注意!三次握手只是用来建立连接用的,和TCP可靠稳定没有关系,TCP的可靠是通过重传和检错等机制实现的。 默认创建一个socket后ÿ…...
爬山算法全解析:掌握优化技巧,攀登技术高峰!
一、引言 爬山算法是一种局部搜索算法,它基于当前解的邻域中进行搜索,通过比较当前解与邻域解的优劣来更新当前解,从而逐步逼近最优解。本文将对爬山算法进行详细的介绍。 二、爬山算法简介 爬山算法是一种基于贪心策略的优化算法ÿ…...
使用 Ollama框架 下载和使用 Llama3 AI大模型的完整指南
🏡作者主页:点击! 🤖AI大模型部署与应用专栏:点击! ⏰️创作时间:2024年5月24日20点59分 🀄️文章质量:96分 目录 💥Ollama介绍 主要特点 主要优点 应…...
最新流媒体在线音乐系统网站源码| 音乐社区 | 多语言 | 开心版
最新流媒体在线音乐系统网站源码 源码免费下载地址抄笔记 (chaobiji.cn)...
中国改革报是什么级别的报刊?在哪些领域具有较高的影响力?
中国改革报是什么级别的报刊?在哪些领域具有较高的影响力? 《中国改革报》是国家发展和改革委员会主管的全国性综合类报纸。它在经济领域和改革发展方面具有重要的影响力,是传递国家政策、反映改革动态的重要平台。该报对于推动中国的经济改…...
乡村振兴的乡村公共服务提升:提升乡村公共服务水平,满足农民多样化需求,构建幸福美好的美丽乡村
目录 一、引言 二、乡村公共服务提升的必要性 (一)满足农民多样化需求 (二)促进乡村经济发展 (三)构建幸福美好的美丽乡村 三、乡村公共服务面临的挑战 (一)基础设施薄弱 &a…...

【在 Windows 上使用 ADB 安装 Android 设备上的 atx-agent】
在进行 Android 应用的 UI 自动化测试时,通常需要在设备上安装一些辅助工具。其中一个常用的工具是 atx-agent,它可以帮助我们在 Android 设备上进行 UI 自动化操作。本文将介绍如何在 Windows 环境下使用 ADB 安装 Android 设备上的 atx-agent。 1. 下…...

iptables 防火墙
linux防火墙基础 iptables的表,链结构 数据包控制的匹配流程 编写防火墙规则 基本语法,控制类型 添加,查看,删除规则 规则的匹配条件 iptables组件 netfilter :属于内核态的功能体系,是一个内核模块…...
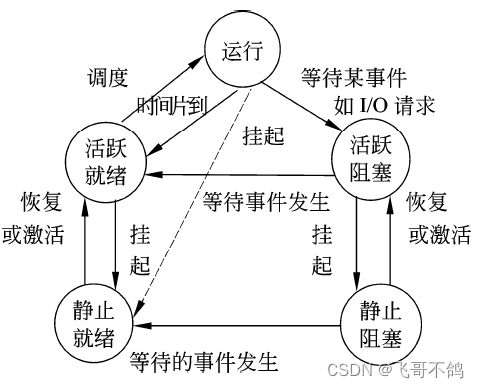
软件设计师笔记1
分享一下学习软考时做的笔记,笔者太懒了,后续篇章都没咋记录,现在放出来水几篇文章 另外,本章内容都是结合教材,B站课堂记录。下一篇软考笔记知识点来自真题 软考笔记 第一章 1. 计算机的组成 1. 控制器 控制器由…...

springboot集成mybatis 单元测试
1、依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0…...

ecc dsa rsa des
ECC(椭圆曲线密码学)、DSA(数字签名算法)、RSA(一种公钥加密技术)和DES(数据加密标准)都是密码学领域中重要的加密和安全技术。下面是对这四种技术的简要介绍: 椭圆曲线密…...
)
Gitee的原理及应用详解(三)
本系列文章简介: Gitee是一款开源的代码托管平台,是国内最大的代码托管平台之一。它基于Git版本控制系统,提供了代码托管、项目管理、协作开发、代码审查等功能,方便团队协作和项目管理。Gitee的出现,在国内的开发者社…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...