排序题目:最小绝对差
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:最小绝对差
出处:1200. 最小绝对差
难度
2 级
题目描述
要求
给定整数数组 arr \texttt{arr} arr,其中每个元素都不相同,找到所有具有最小绝对差的元素对。
按升序的顺序返回元素对列表,每个元素对 [a, b] \texttt{[a, b]} [a, b] 满足:
- a, b \texttt{a, b} a, b 是数组 arr \texttt{arr} arr 中的元素。
- a < b \texttt{a} < \texttt{b} a<b。
- b − a \texttt{b} - \texttt{a} b−a 等于数组 arr \texttt{arr} arr 中的任意两个元素的最小绝对差。
示例
示例 1:
输入: arr = [4,2,1,3] \texttt{arr = [4,2,1,3]} arr = [4,2,1,3]
输出: [[1,2],[2,3],[3,4]] \texttt{[[1,2],[2,3],[3,4]]} [[1,2],[2,3],[3,4]]
解释:最小绝对差是 1 \texttt{1} 1。将所有绝对差等于 1 \texttt{1} 1 的元素对按升序的顺序加入列表并返回。
示例 2:
输入: arr = [1,3,6,10,15] \texttt{arr = [1,3,6,10,15]} arr = [1,3,6,10,15]
输出: [[1,3]] \texttt{[[1,3]]} [[1,3]]
示例 3:
输入: arr = [3,8,-10,23,19,-4,-14,27] \texttt{arr = [3,8,-10,23,19,-4,-14,27]} arr = [3,8,-10,23,19,-4,-14,27]
输出: [[-14,-10],[19,23],[23,27]] \texttt{[[-14,-10],[19,23],[23,27]]} [[-14,-10],[19,23],[23,27]]
数据范围
- 2 ≤ arr.length ≤ 10 5 \texttt{2} \le \texttt{arr.length} \le \texttt{10}^\texttt{5} 2≤arr.length≤105
- -10 6 ≤ arr[i] ≤ 10 6 \texttt{-10}^\texttt{6} \le \texttt{arr[i]} \le \texttt{10}^\texttt{6} -106≤arr[i]≤106
解法
思路和算法
当数组有序时,每个元素的相邻元素是数组中与该元素最接近的元素,因此最小绝对差一定是排序后的数组中的两个相邻元素之差。
首先将数组排序,然后遍历排序后的数组,计算每一对相邻元素的绝对差,即可得到最小绝对差。
得到最小绝对差之后,再次遍历排序后的数组,计算每一对相邻元素的绝对差,当相邻元素的绝对差等于最小绝对差时,将这一对相邻元素添加到结果列表中,遍历结束之后即可得到所有具有最小绝对差的元素对。
由于是遍历排序后的数组寻找具有最小绝对差的元素对,因此遍历元素对的顺序是递增顺序,可以确保结果列表中的元素对按升序的顺序排列。
代码
class Solution {public List<List<Integer>> minimumAbsDifference(int[] arr) {Arrays.sort(arr);int minDiff = arr[1] - arr[0];int length = arr.length;for (int i = 2; i < length; i++) {minDiff = Math.min(minDiff, arr[i] - arr[i - 1]);}List<List<Integer>> pairs = new ArrayList<List<Integer>>();for (int i = 1; i < length; i++) {if (arr[i] - arr[i - 1] == minDiff) {List<Integer> pair = new ArrayList<Integer>();pair.add(arr[i - 1]);pair.add(arr[i]);pairs.add(pair);}}return pairs;}
}
复杂度分析
-
时间复杂度: O ( n log n ) O(n \log n) O(nlogn),其中 n n n 是数组 arr \textit{arr} arr 的长度。排序需要 O ( n log n ) O(n \log n) O(nlogn) 的时间,每次遍历数组需要 O ( n ) O(n) O(n) 的时间,总时间复杂度是 O ( n log n ) O(n \log n) O(nlogn)。
-
空间复杂度: O ( log n ) O(\log n) O(logn),其中 n n n 是数组 arr \textit{arr} arr 的长度。排序需要 O ( log n ) O(\log n) O(logn) 的递归调用栈空间。注意返回值不计入空间复杂度。
相关文章:

排序题目:最小绝对差
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:最小绝对差 出处:1200. 最小绝对差 难度 2 级 题目描述 要求 给定整数数组 arr \texttt{arr} arr,其中每个元素都不相同&…...

沃飞携AE200真机亮相澳门,全方位赋能城市低空出行
5月22日-25日,第四届BEYOND国际科技创新博览会(BEYOND Expo 2024)在澳门盛大举行。吉利沃飞长空携旗下全自研产品AE200真机亮相,吸引了现场众多领导嘉宾以及媒体、观众的关注。 作为亚洲顶尖的年度科技盛会,本届BEYOND…...
)
判断当前系统是linux、windows还是MacOS (python)
在很多情况下,需要在python中获取当前系统的类型,用于判断是unix/windows/mac或者java虚拟机等,python中提供了os.name, sys.platform, platform.system等方式 sys sys.platform会返回当前系统平台的标识符ÿ…...

Minikube部署单节点Kubernetes
1.1 Minikube部署单节点K8s Minikube是由Kubernetes社区维护的单机版的Kubernetes集群,支持macOS, Linux, andWindows等多种操作系统平台,使用最新的官方stable版本,并支持Kubernetes的大部分功能,从基础的容器编排管理࿰…...
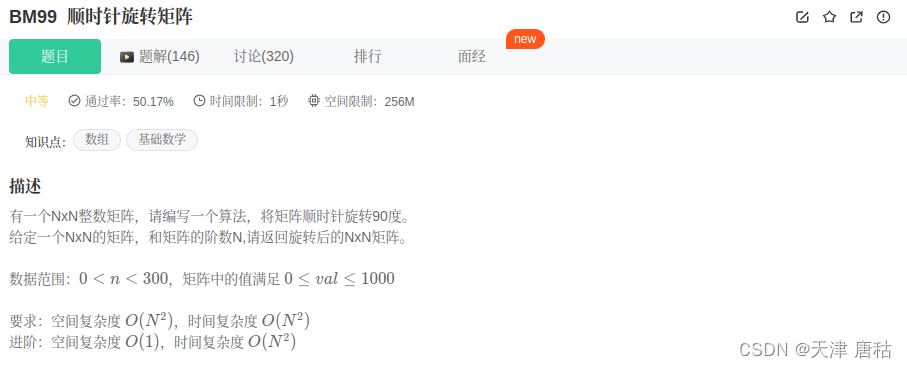
leetcode-顺时针旋转矩阵-111
题目要求 思路 1.假设现在有一个矩阵 123 456 789 2.我们可以根据19这个对角线将数据进行交换,得到矩阵 147 258 369 3.然后将矩阵每一行的数据再翻转,得到矩阵 741 852 963 代码实现 class Solution { public:vector<vector<int> > rot…...

解决GoLand无法Debug
goland 调试的的时候提示如下错误 WARNING: undefined behavior - version of Delve is too old for Go version 1.22.3 (maximum supported v 其实个原因是因为正在使用的Delve调试器版本太旧,无法兼容当前的Go语言版本1.22.3。Delve是Go语言的一个调试工具&#…...

云原生周刊:K8s 上的 gRPC 名称解析和负载平衡
开源项目推荐 Kraken Kraken 是一个基于 P2P 的 Docker 注册表,专注于可扩展性和可用性。它专为混合云环境中的 Docker 镜像管理、复制和分发而设计。借助可插拔的后端支持,Kraken 可以轻松集成到现有的 Docker 注册表设置中作为分发层。 E2E Framewo…...
从0开始回顾ElasticSearch
1 elasticsearch概述 1.1 elasticsearch简介 官网: https://www.elastic.co/ ElasticSearch是一个基于Lucene的搜索服务器。它提供了一个分布式多用户能力的全文搜索引擎,基于RESTful web接口。Elasticsearch是用Java开发的,并作为Apache许可条款下的…...

小阿轩yx-Shell编程之条件语句
小阿轩yx-Shell编程之条件语句 条件测试操作 Shell 环境根据命令执行后的返回状态值($?)来判断是否执行成功 返回值 为 0 时:表示成功否则(非 0 值)表示失败或异常 测试工具 test 命令,对特定条件进行…...

MyBatis-Plus 从入门到精通
MyBatis-Plus 从入门到精通 前言快速入门创建一个SpringBoot项目导入依赖配置数据库创建一个实体类创建一个mapper接口在SpringBoot启动类上配置mapper接口的扫描路径在数据库中创建表编写一个SpringBoot测试类 核心功能注解CRUD接口Mapper CRUD接口Service CRUD 接口条件构造器…...
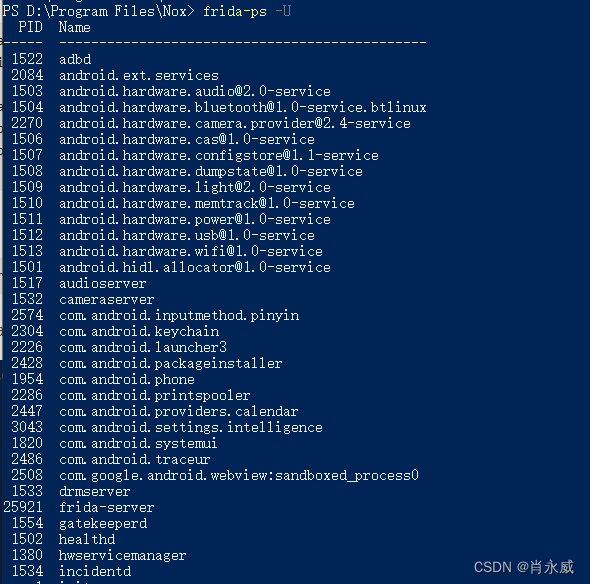
爬虫利器Frida RPC入门——夜神模拟器环境篇
Frida是一款轻量级HOOK框架,可用于多平台上,例如android、windows、ios等。 frida分为两部分,服务端运行在目标机上,通过注入进程的方式来实现劫持应用函数,另一部分运行在系统机器上。frida上层接口支持js、python、…...
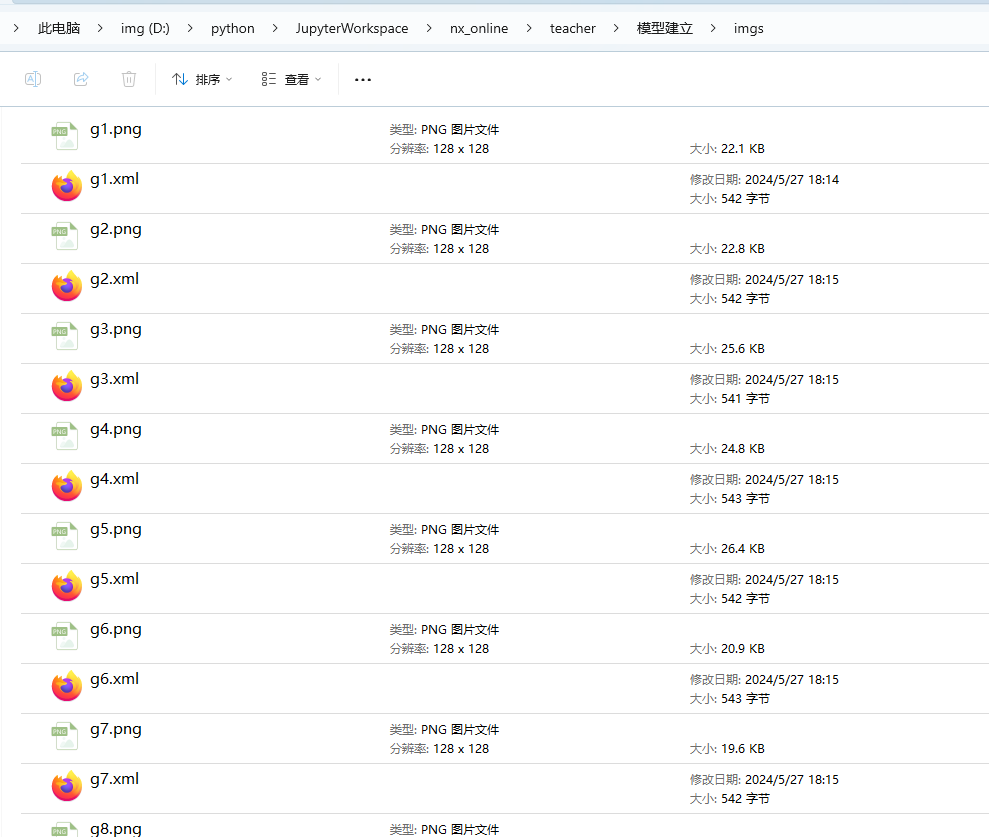
猫狗分类识别模型建立①数据标记
一、labelImg库说明 LabelImg是一款非常流行的图像标注工具,广泛用于机器学习和计算机视觉领域。以下是关于LabelImg的详细介绍: 主要功能和特点 1.图像标注 允许用户在图像中标注物体,选择特定区域,并为这些区域添加标签或类…...

FME学习之旅---day28
我们付出一些成本,时间的或者其他,最终总能收获一些什么。 教程:CSV 入门...

vue3项目中字典和全局方法的创建与使用
在src下新建dict.ts/js,写入下面代码 import { App, Plugin } from vue;interface Dict {auditgrouptypeList: { label: string; value: string }[];auditstateList: { label: string; value: string }[];accountchangeList: { label: string; value: number }[]; }const Dict…...
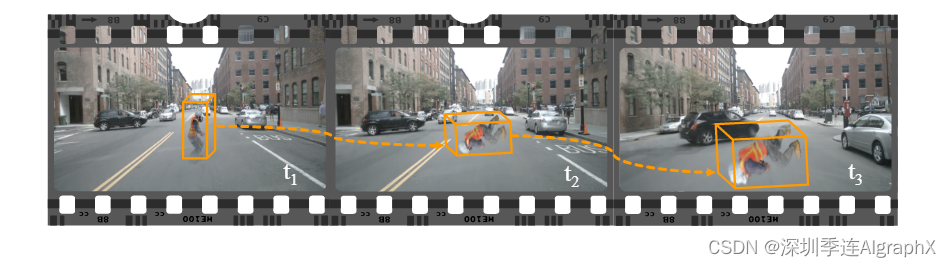
51-54 Sora能制作动作大片还需要一段时间 | DrivingGaussian:周围动态自动驾驶场景的复合高斯飞溅
24年3月,北大、谷歌和加州大学共同发布了DrivingGaussian: Composite Gaussian Splatting for Surrounding Dynamic Autonomous Driving Scenes。视图合成和可控模拟可以生成自动驾驶的极端场景Corner Case,这些安全关键情况有助于以更低成本验证和增强自…...

数据挖掘实战-基于余弦相似度的印度美食推荐系统
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

深入探索DreamFusion:文本到3D生成的革命性技术
深入探索DreamFusion:文本到3D生成的革命性技术 引言: 在人工智能和计算机视觉领域,DreamFusion无疑是一个引人注目的新星。这项技术,基于Google提出的深度学习模型,将自然语言与三维内容生成紧密结合,开…...

JSP期末要点复习
一、JSP工作原理 1.客户端请求JSP页面:用户通过浏览器发送一个请求到服务器,请求一个特定的JSP页面。这个请求被服务器上的Web容器(如Apache Tomcat)接收。 2.JSP转换为Servlet:当JSP页面第一次被请求时࿰…...
)
AJAX(JavaScript版本)
目录 一.AJAX简介 二.XMLHttpRequests对象 2.1XMLHttpRequests对象简介 2.2创建XMLHttpRequests对象 2.3定义回调函数 2.4发送请求 2.5XMLHttpRequests对象方法介绍 2.6XMLHttpRequests对象属性 三.向服务器发送请求 3.1发送请求 3.2使用GET还是POST 3.3使用GET来发…...
框架学习之SpringMVC学习笔记(一)
一、SpringMVC简介 1-介绍 Spring Web MVC是基于Servlet API构建的原始Web框架,从一开始就包含在Spring Framework中。正式名称“Spring Web MVC”来自其源模块的名称( spring-webmvc ),但它通常被称为“Spring MVC”。 在控制层…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
