【数据结构】链式二叉树(超详细)
文章目录
- 前言
- 二叉树的链式结构
- 二叉树的遍历方式
- 二叉树的深度优先遍历
- 前序遍历(先根遍历)
- 中序遍历(中根遍历)
- 后序遍历(后根遍历)
- 二叉树的广度优先遍历
- 层序遍历
- 二叉树链式结构接口实现
- 二叉树结点个数
- 二叉树叶子结点个数
- 二叉树的深度(高度)
- 二叉树第k层结点个数
- 二叉树查找x值的结点
- 销毁二叉树
- 二叉树的创建及遍历
- 衍生题
- 判断二叉树是否为完全二叉树
- 判断二叉树是否为单值二叉树
- 判断两颗二叉树是否相同
- 判断二叉树是否为对称二叉树
- 判断一颗二叉树是否为另一颗二叉树的子树
- 判断二叉树是否为平衡二叉树
- 翻转二叉树
前言
二叉树的顺序结构就是用数组来存储,而「数组」一般只适合表示「满二叉树」或「完全二叉树」,因为不是完全二叉树会有「空间的浪费」。
普通二叉树的增删查改没有意义,主要学习它的结构,要加上搜索树的规则,才有价值。
二叉树的链式结构
二叉树链式结构的实现
在学习二叉树的基本操作前,需先要创建一棵二叉树,这里手动快速创建一棵简单的二叉树
#include<stdio.h> // perror, printf
#include<stdlib.h> // malloctypedef char BTDataType;
// 定义二叉树的结点
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 动态申请一个新结点
BTNode* BuyNode(BTDataType x)
{// BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc");exit(-1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}// 二叉树的链式结构
BTNode* CreatBinaryTree()
{// 创建多个结点BTNode* node_A = BuyNode('A');BTNode* node_B = BuyNode('B');BTNode* node_C = BuyNode('C');BTNode* node_D = BuyNode('D');BTNode* node_E = BuyNode('E');BTNode* node_F = BuyNode('F');// 用链来指示结点间的逻辑关系node_A->left = node_B;node_A->right = node_C;node_B->left = node_D;node_C->left = node_E;node_C->right = node_F;return node_A;
}注意:上述代码并不是创建二叉树的方式
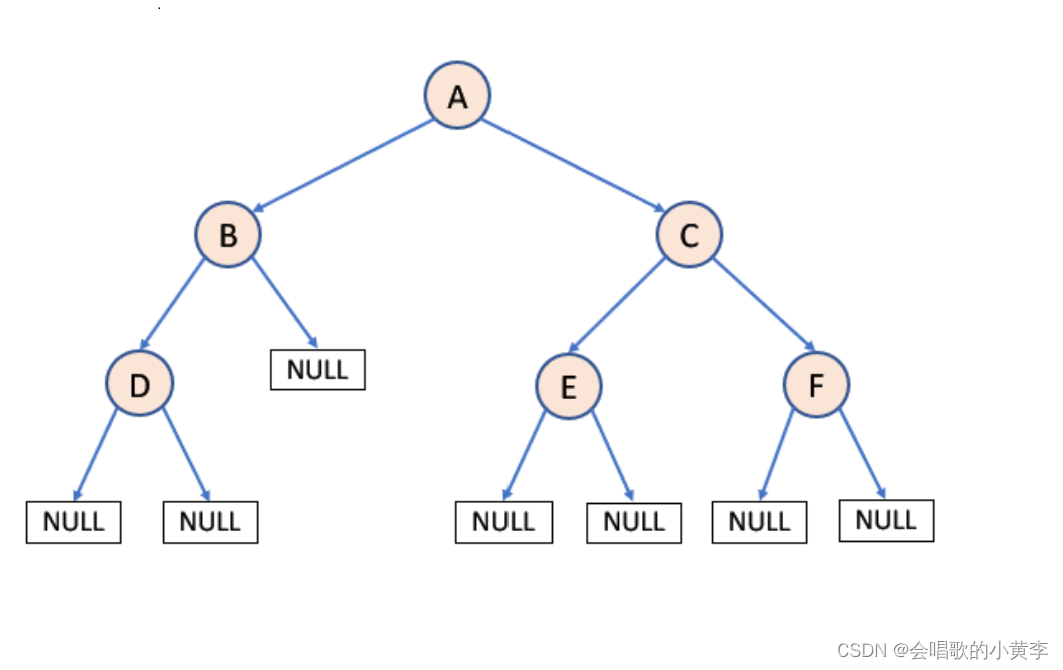
二叉树的遍历方式
二叉树的深度优先遍历
由于被访问的结点必是「某子树的根」,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
前序遍历(先根遍历)
遍历顺序:根->左子树->右子树
//前序遍历
void BinaryPrevOrder(BTNode* root)
{if (root == NULL){return;}//根->左子树->右子树printf("%c ", root->data);BinaryPrevOrder(root->left);BinaryPrevOrder(root->right);
}这里的访问路径是:A B D NULL NULL NULL C E NULL NULL F NULL NULL

接下来的两个遍历可以自己试试画一下递归图。
中序遍历(中根遍历)
遍历顺序:左子树->根->右子树
void BinaryInOrder(BTNode* root)
{if (root == NULL){return;}//左子树->根->右子树BinaryInOrder(root->left);printf("%c ", root->data);BinaryInOrder(root->right);
}这里的访问路径是:NULL D NULL B NULL A NULL E NULL C NULL F NULL
后序遍历(后根遍历)
遍历顺序:左子树->右子树->根
//后序遍历
void BinaryPostOrder(BTNode* root)
{if (root == NULL){return;}//左子树->右子树->根BinaryPostOrder(root->left);BinaryPostOrder(root->right);printf("%c ", root->data);
}这里的访问路径是:NULL NULL D NULL B NULL NULL E NULL NULL F C A
二叉树的广度优先遍历
层序遍历
层序遍历,自上而下,从左往右逐层访问树的结点的过程就是层序遍历。
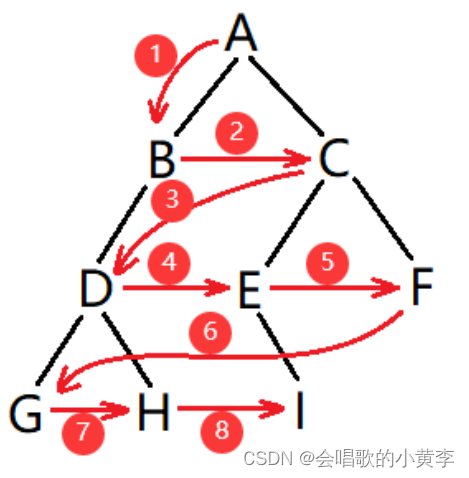
我们借助队列来实现:
先入根结点,然后出队列,再入他的两个孩子,然后一样的出孩子,再入孩子的孩子,重复即可。(NULL不入)

//层序遍历
void BinaryLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//初始化队列if (root != NULL)QueuePush(&q, root);int levelSize = 1;while (!QueueEmpty(&q))//当队列不为空时,循环继续{//一层一层出while (levelSize--){BTNode* front = QueueFront(&q);//读取队头元素QueuePop(&q);//删除队头元素printf("%c ", front->data);//打印出队的元素if (front->left){QueuePush(&q, front->left);//出队元素的左孩子入队列}if (front->right){QueuePush(&q, front->right);//出队元素的右孩子入队列}}printf("\n");levelSize = QueueSize(&q);}printf("\n");QueueDestroy(&q);//销毁队列
}
二叉树链式结构接口实现
二叉树结点个数
子问题拆解:
1.若为空,则结点个数为0。
2.若不为空,则结点个数 = 左子树结点个数 + 右子树结点个数 + 1(自己)。
//结点的个数
int BinaryTreeSize(BTNode* root)
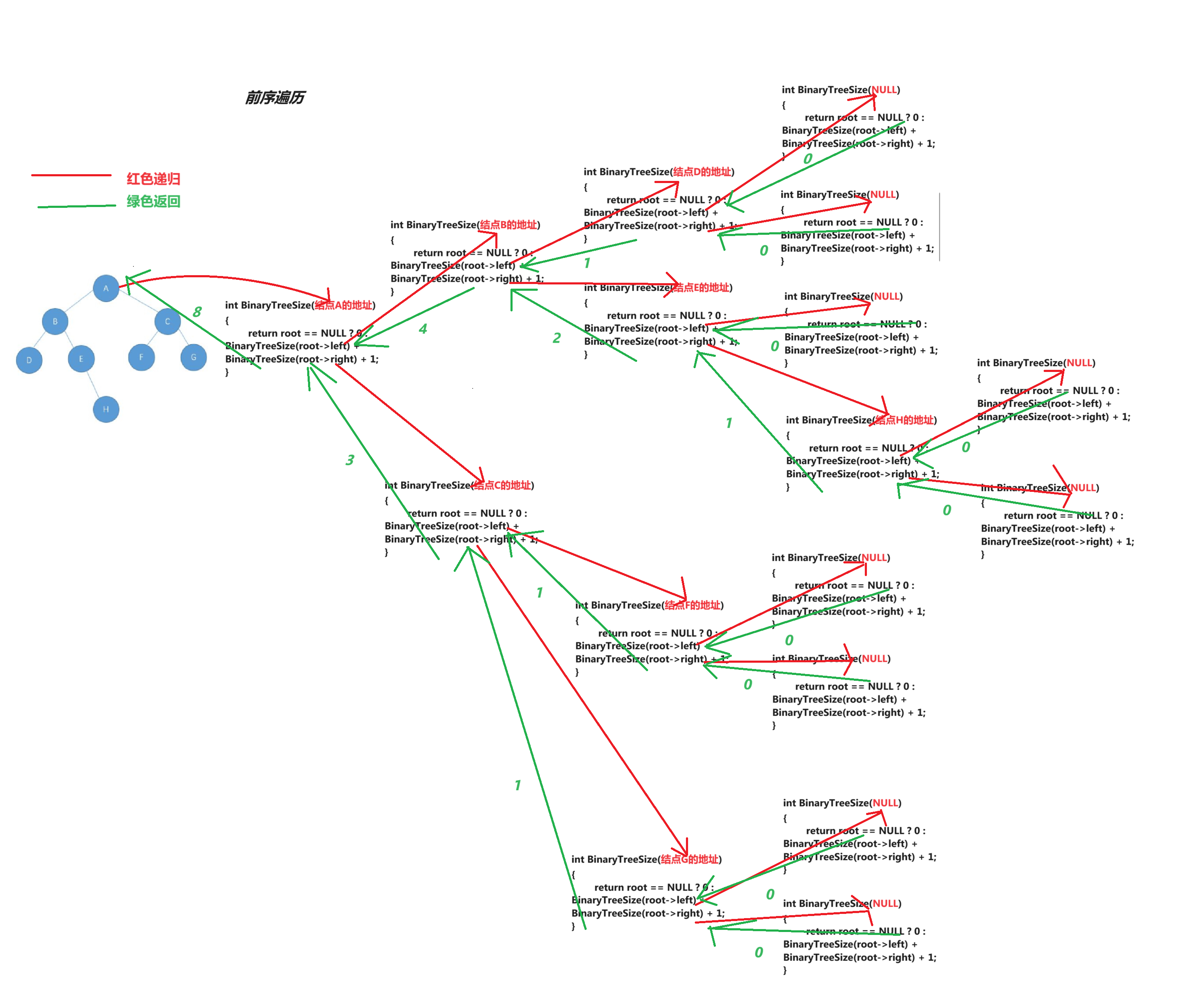
{//结点个数 = 左子树的结点个数 + 右子树的结点个数 + 自己return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
二叉树叶子结点个数
子问题拆解:
1.若为空,则叶子结点个数为0。
2.若结点的左指针和右指针均为空,则叶子结点个数为1。
3.除上述两种情况外,说明该树存在子树,其叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数。
//叶子结点的个数
int BinaryTreeLeafSize(BTNode* root)
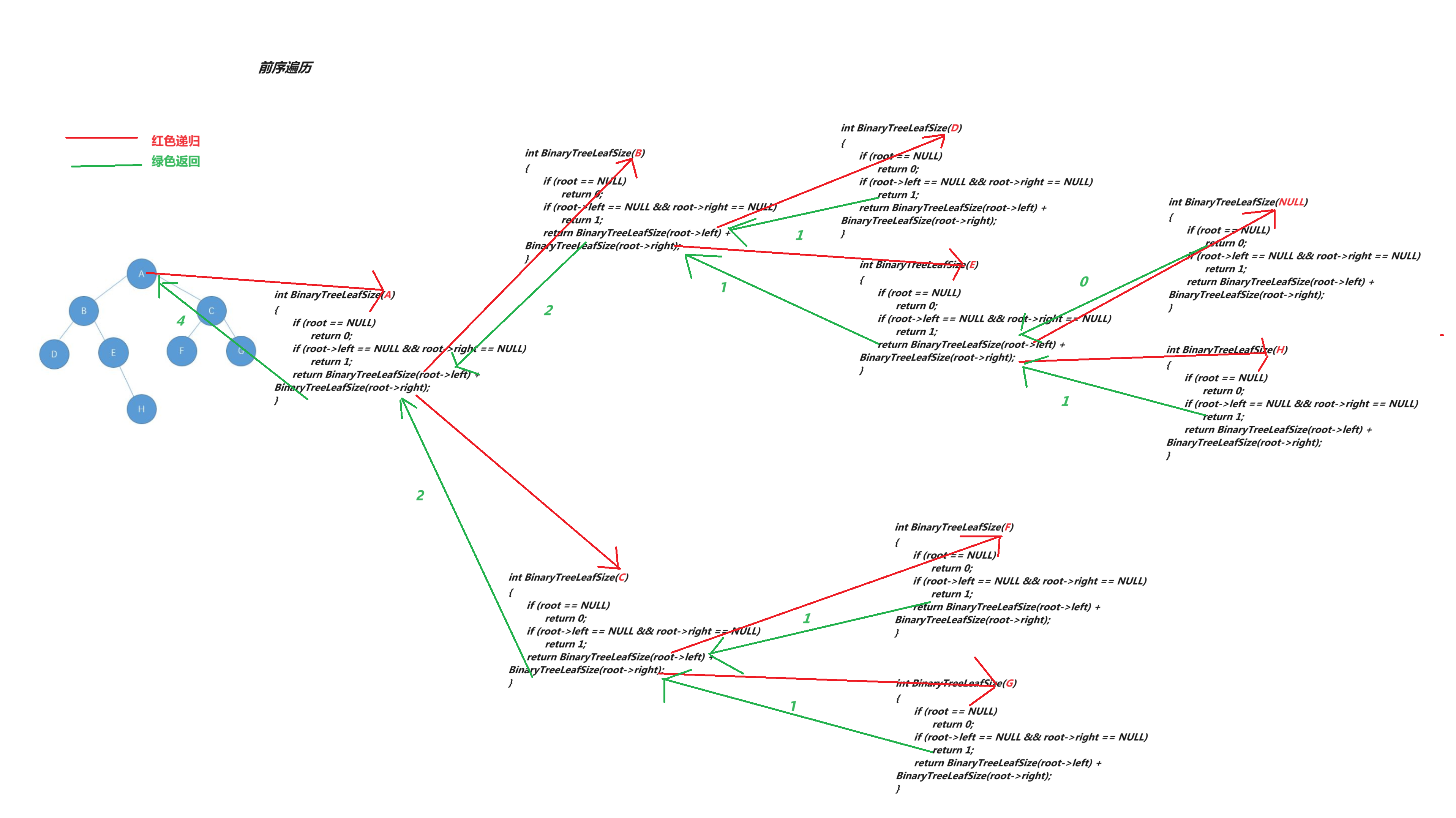
{if (root == NULL)//空树无叶子结点return 0;if (root->left == NULL && root->right == NULL)//是叶子结点return 1;//叶子结点的个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
二叉树的深度(高度)
子问题拆解:
- 先判断当前树的根结点是否为空
- 当前树的根结点不为空,分别计算其左右子树的深度
- 比较当前树左右子树的深度,最大的那个+1 就是当前树的深度
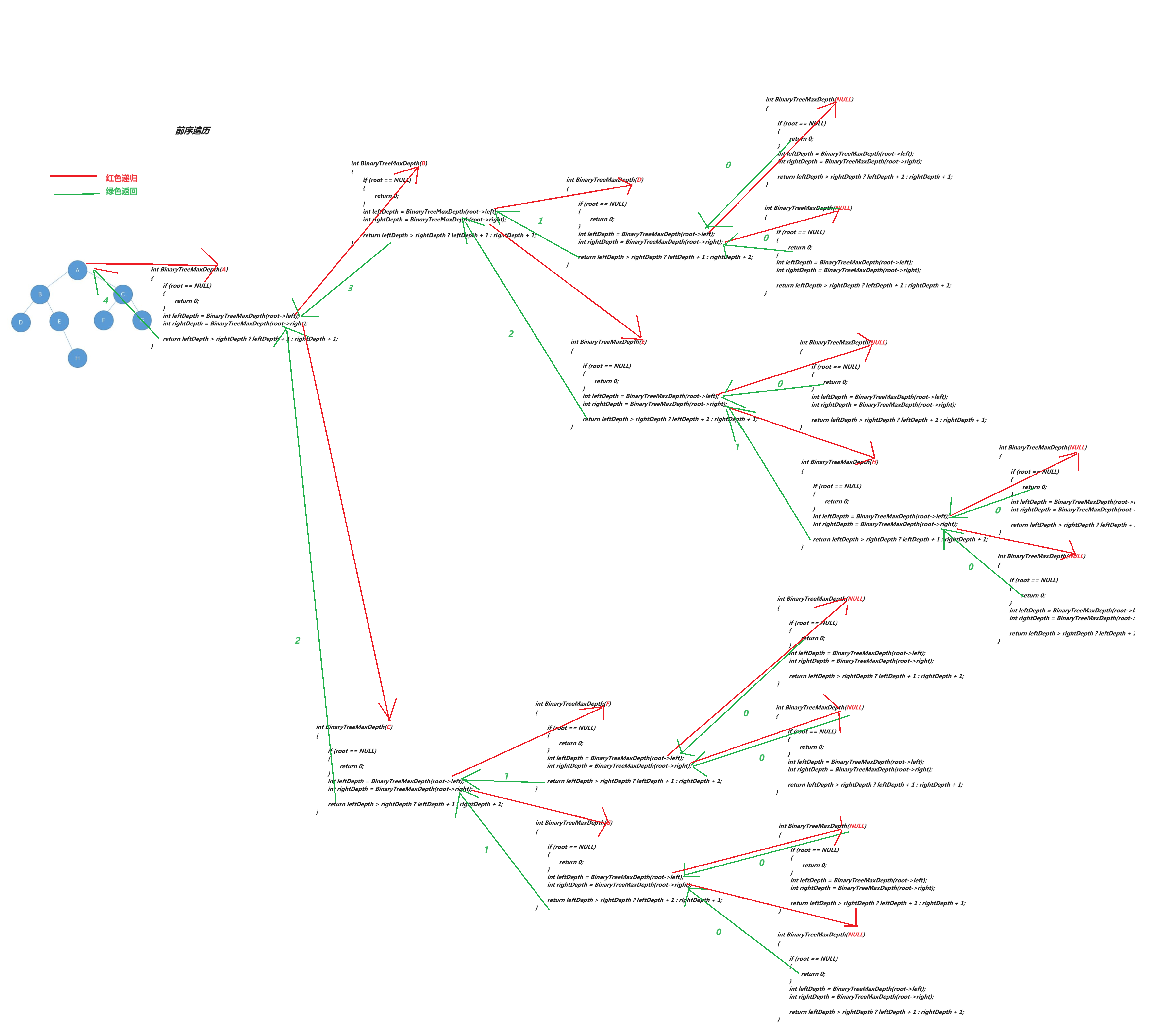
// 二叉树的深度(高度)
int BinaryTreeMaxDepth(BTNode* root)
{// 先判断当前树的根结点是否为空if (root == NULL){return 0;}// 当前树的根结点不为空,分别计算其左右子树的深度int leftDepth = BinaryTreeMaxDepth(root->left);int rightDepth = BinaryTreeMaxDepth(root->right);// 比较当前树左右子树的深度,最大的那个+1 就是当前树的深度return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
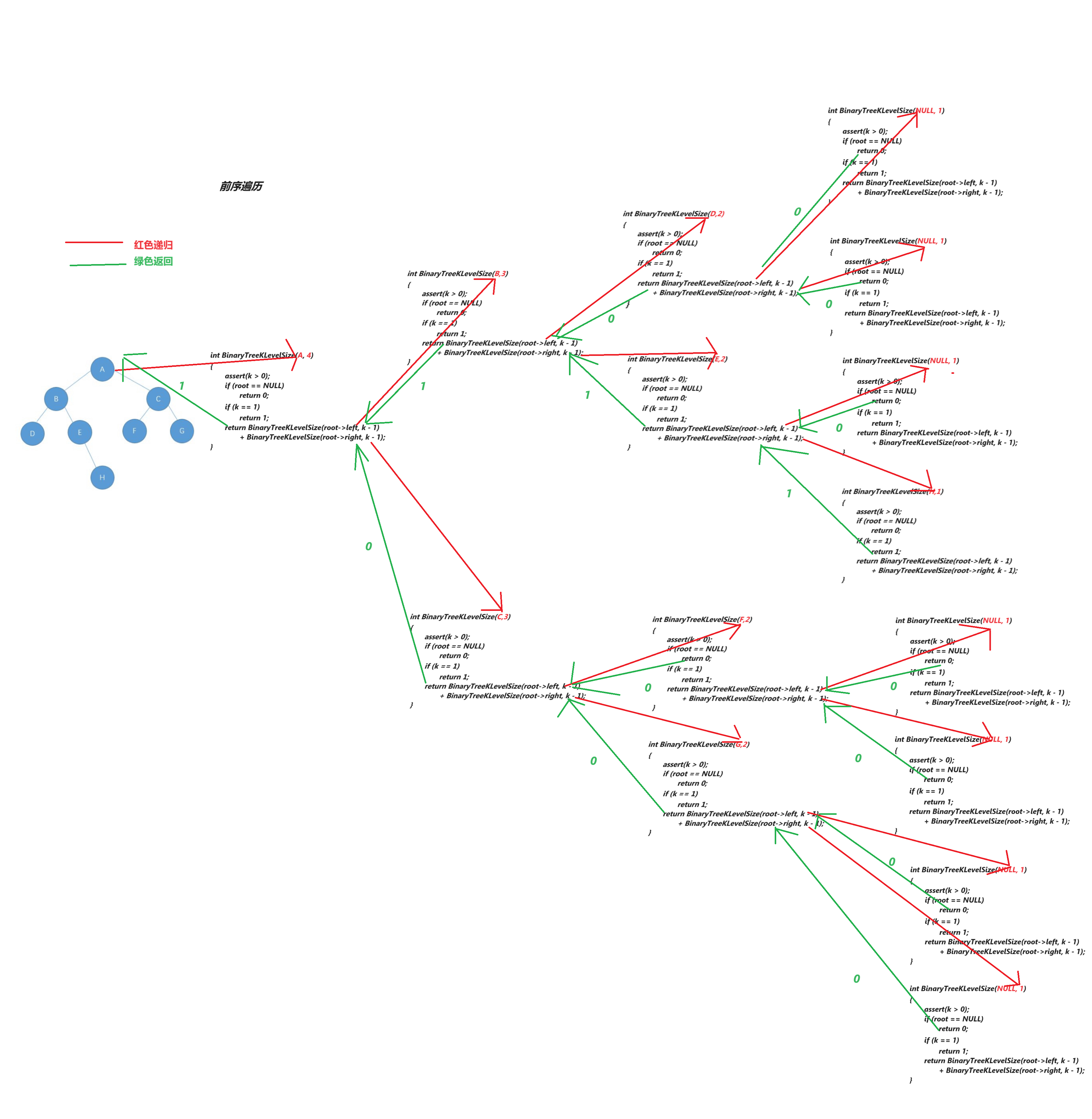
二叉树第k层结点个数
//第k层结点的个数O(N)
int BinaryTreeKLevelSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)//第一层结点个数return 1;//相对于父结点的第k层的结点个数 = 相对于两个孩子结点的第k-1层的结点个数之和return BinaryTreeKLevelSize(root->left, k - 1) + BinaryTreeKLevelSize(root->right, k - 1);
}
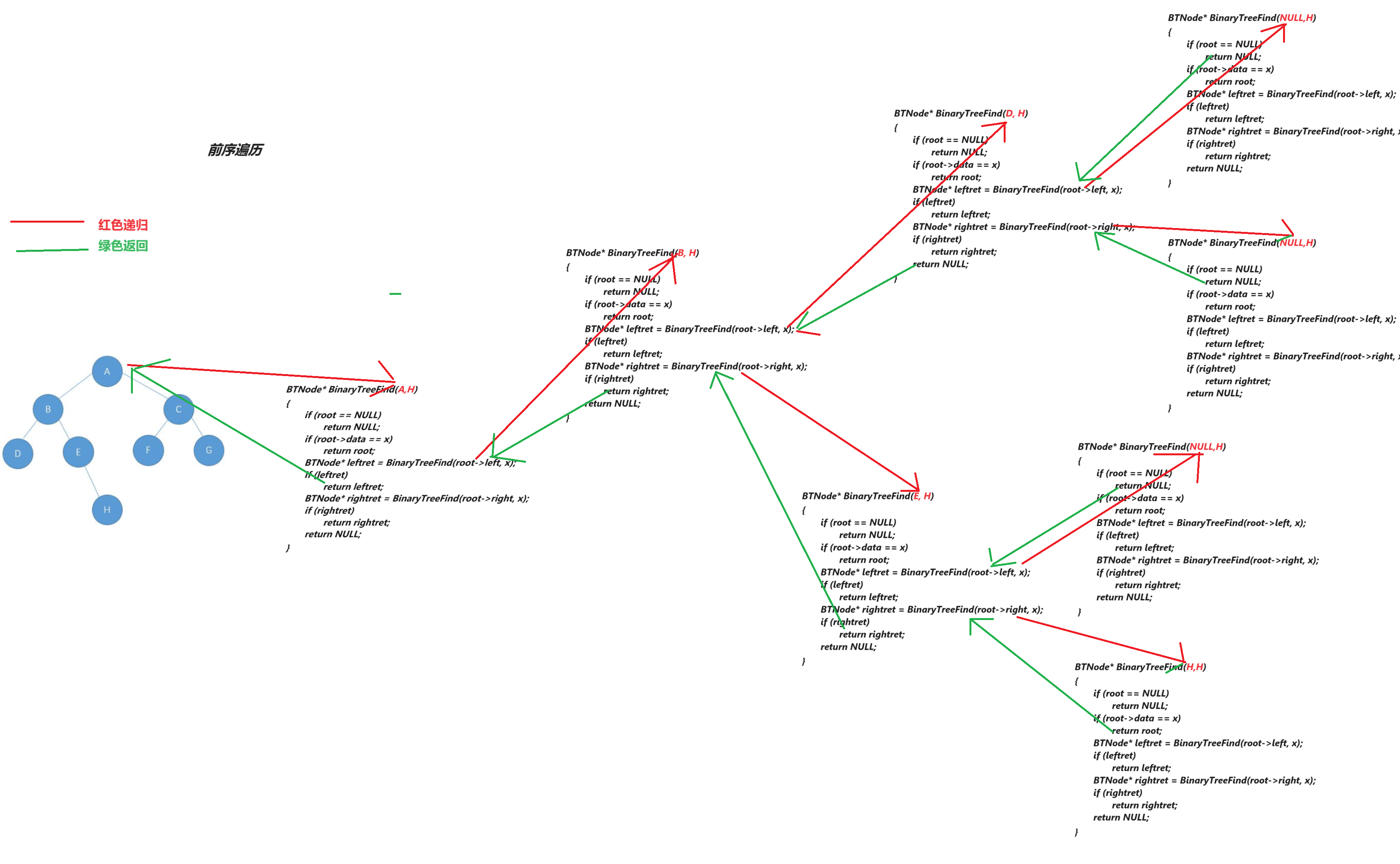
二叉树查找x值的结点
//查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)//空树return NULL;if (root->data == x)//先判断根结点return root;BTNode* leftret = BinaryTreeFind(root->left, x);//在左子树中找if (leftret)return leftret;BTNode* rightret = BinaryTreeFind(root->right, x);//在右子树中找if (rightret)return rightret;return NULL;//根结点和左右子树中均没有找到
}
销毁二叉树
这里要用后序遍历来销毁,左子树->右子树->根
//销毁二叉树
void BinaryTreeDestroy(BTNode* root)
{if (root == NULL)return;BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);free(root);//没有用二级指针,这里只是实参的拷贝,需要用完主动置空再函数外置空}
二叉树的创建及遍历
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。
例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
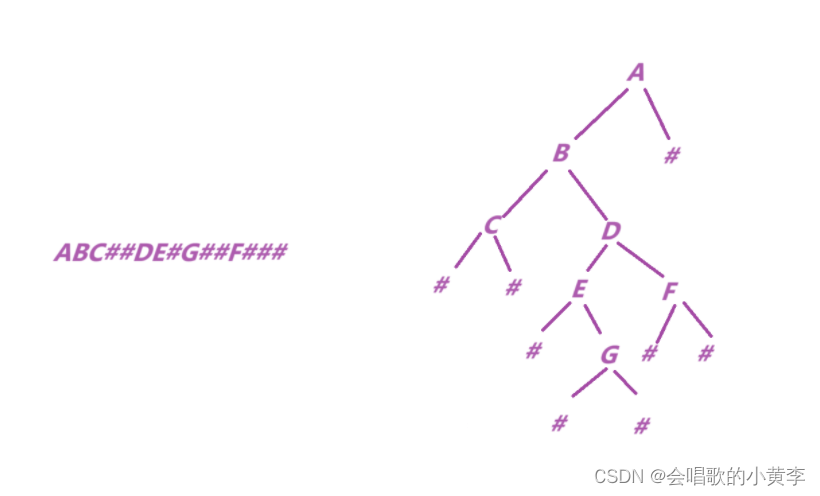
依次读取字符,拆分成子问题:
1.如果不是#,创建结点,存值,然后递归其左子树和右子树;
2.如果是#,说明不能构建结点了,直接返回NULL;
#include <stdio.h>typedef char BTDataType;
typedef struct BinaryTreeNode{BTDataType data;struct BinaryTreeNode*left;struct BinaryTreeNode*right;}BTNode;BTNode*BinaryTreeCreat(char*arr,int*pi)
{if(arr[*pi]=='#'){(*pi)++;return NULL;}BTNode*node=(BTNode*)malloc(sizeof(BTNode));node->data=arr[*pi];(*pi)++;node->left=NULL;node->right=NULL;
node->left=BinaryTreeCreat(arr,pi);//递归构建左子树
node->right=BinaryTreeCreat(arr,pi);//递归构建右子树
return node;
}//中序遍历
void BinaryInOrder(BTNode*root)
{if(root==NULL)return;BinaryInOrder(root->left);printf("%c ",root->data);BinaryInOrder(root->right);
}int main() {
char ret[100];
scanf("%s",&ret );
int i=0;
BTNode*root= BinaryTreeCreat(ret,&i);
BinaryInOrder(root);
printf("\n");return 0;
}
衍生题
判断二叉树是否为完全二叉树
用一个队列来判断
将根从队尾入列,然后从队头出数据,出根的时候入它的左孩子和右孩子,NULL也入列。重复次操作,当出数据第一次遇到NULL时,停止入队列并且检查队列中是否还有数据,如果全部为NULL则此树时完全二叉树
如果队列中还有数据,则不是完全二叉树。
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);//初始化队列if (root != NULL)QueuePush(&q, root);while (!QueueEmpty(&q))//当队列不为空时,循环继续{BTNode* front = QueueFront(&q);//读取队头元素QueuePop(&q);//删除队头元素//遇到第一个NULL结点直接跳出循环if (front == NULL)break;QueuePush(&q, front->left);//出队元素的左孩子入队列(NULL也入)QueuePush(&q, front->right);//出队元素的右孩子入队列(NULL也入)}//前面遇到空以后,后面还有非空就不是完全二叉树while (!QueueEmpty(&q))//当队列不为空时,循环继续{BTNode* front = QueueFront(&q);//读取队头元素QueuePop(&q);//删除队头元素if (front){QueueDestroy(&q);//销毁队列return false;}}//没有遇到说明是完全二叉树QueueDestroy(&q);//销毁队列return true;
}
判断二叉树是否为单值二叉树
单值二叉树,所有结点的值都相同的二叉树即为单值二叉树,判断某一棵二叉树是否是单值二叉树的一般步骤如下:
1.判断根的左孩子的值与根结点是否相同。
2.判断根的右孩子的值与根结点是否相同。
3.判断以根的左孩子为根的二叉树是否是单值二叉树。
4.判断以根的右孩子为根的二叉树是否是单值二叉树。
若满足以上情况,则是单值二叉树。
bool isUnivalTree(struct TreeNode* root) {if(root==NULL)return true;if(root->left&&root->left->val!=root->val) return false;if(root->right&&root->right->val!=root->val)return false;return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
判断两颗二叉树是否相同
拆分成子问题:
先判断根是否为空
再比较根的左子树是否相同
再比较跟根的右子树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if(p==NULL&&q==NULL)return true;if(p==NULL||q==NULL)return false;if(p->val!=q->val)return false;return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
判断二叉树是否为对称二叉树
实际上就是要判断根节点的左右两个子树是否镜像对称。因此,其解决方案为:按照对称的方式遍历左右子树,比较同时遍历的节点是否一致。而且在遍历过程中,只有两个子树的根节点对称了,继续比较左右子树是否对称才有意义,因此我们使用"中序遍历"(其实不是严格的中序遍历,只是我们先比较根节点)
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p==NULL&&q==NULL)return true;if(p==NULL||q==NULL)return false;if(p->val!=q->val)return false;return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);}bool isSymmetric(struct TreeNode* root) {if(root==NULL)return true;return isSameTree(root->left,root->right);}
判断一颗二叉树是否为另一颗二叉树的子树
两个树都是空树,返回true
如果两个树一个是空,一个不是空,不包含
两个树都是非空,比较根节点的值是不是相等,如果相等的话,比较一下p和q是不是相同的树
递归的判定一下,p是否被q的左子树包含
递归的判定一下,p是否被q的右子树包含。
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p==NULL&&q==NULL)return true;if(p==NULL||q==NULL)return false;if(p->val!=q->val)return false;return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root==NULL)return false;if(isSameTree(root->left,subRoot))return true;return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);}
判断二叉树是否为平衡二叉树
如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
子问题:
求出左子树的深度。
求出右子树的深度。
若左子树与右子树的深度差的绝对值不超过1,并且左右子树也是平衡二叉树,则该树是平衡二叉树。
int max(int x, int y)
{return x>y?x:y;
}
int height(struct TreeNode* root)
{if (root == NULL) return 0;return max(height(root->left), height(root->right)) + 1;
}bool isBalanced(struct TreeNode* root)
{if (root == NULL) return true;//左右子树高度差的绝对值不超过1 && 其左子树是平衡二叉树 && 其右子树是平衡二叉树return fabs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) &&isBalanced(root->right);//fabs取绝对值,要用要包含头文件#include<math.h>
}
翻转二叉树
子问题:
翻转左子树。
翻转右子树。
交换左右子树的位置。
//翻转二叉树
struct TreeNode* invertTree(struct TreeNode* root)
{if (root == NULL)//根为空,直接返回return root;struct TreeNode* left = invertTree(root->left);//翻转左子树struct TreeNode* right = invertTree(root->right);//翻转右子树//左右子树位置交换root->left = right;root->right = left;return root;
}
相关文章:

【数据结构】链式二叉树(超详细)
文章目录 前言二叉树的链式结构二叉树的遍历方式二叉树的深度优先遍历前序遍历(先根遍历)中序遍历(中根遍历)后序遍历(后根遍历) 二叉树的广度优先遍历层序遍历 二叉树链式结构接口实现二叉树结点个数二叉树叶子结点个数二叉树的深度(高度)二叉树第k层结…...

排序题目:最小绝对差
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:最小绝对差 出处:1200. 最小绝对差 难度 2 级 题目描述 要求 给定整数数组 arr \texttt{arr} arr,其中每个元素都不相同&…...

沃飞携AE200真机亮相澳门,全方位赋能城市低空出行
5月22日-25日,第四届BEYOND国际科技创新博览会(BEYOND Expo 2024)在澳门盛大举行。吉利沃飞长空携旗下全自研产品AE200真机亮相,吸引了现场众多领导嘉宾以及媒体、观众的关注。 作为亚洲顶尖的年度科技盛会,本届BEYOND…...
)
判断当前系统是linux、windows还是MacOS (python)
在很多情况下,需要在python中获取当前系统的类型,用于判断是unix/windows/mac或者java虚拟机等,python中提供了os.name, sys.platform, platform.system等方式 sys sys.platform会返回当前系统平台的标识符ÿ…...

Minikube部署单节点Kubernetes
1.1 Minikube部署单节点K8s Minikube是由Kubernetes社区维护的单机版的Kubernetes集群,支持macOS, Linux, andWindows等多种操作系统平台,使用最新的官方stable版本,并支持Kubernetes的大部分功能,从基础的容器编排管理࿰…...
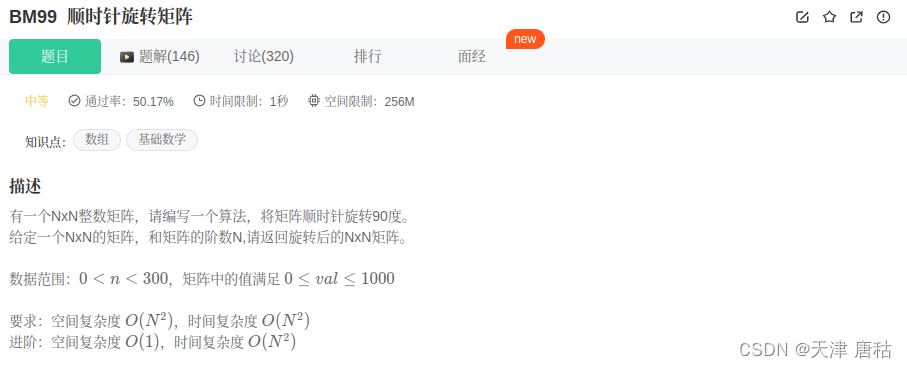
leetcode-顺时针旋转矩阵-111
题目要求 思路 1.假设现在有一个矩阵 123 456 789 2.我们可以根据19这个对角线将数据进行交换,得到矩阵 147 258 369 3.然后将矩阵每一行的数据再翻转,得到矩阵 741 852 963 代码实现 class Solution { public:vector<vector<int> > rot…...

解决GoLand无法Debug
goland 调试的的时候提示如下错误 WARNING: undefined behavior - version of Delve is too old for Go version 1.22.3 (maximum supported v 其实个原因是因为正在使用的Delve调试器版本太旧,无法兼容当前的Go语言版本1.22.3。Delve是Go语言的一个调试工具&#…...

云原生周刊:K8s 上的 gRPC 名称解析和负载平衡
开源项目推荐 Kraken Kraken 是一个基于 P2P 的 Docker 注册表,专注于可扩展性和可用性。它专为混合云环境中的 Docker 镜像管理、复制和分发而设计。借助可插拔的后端支持,Kraken 可以轻松集成到现有的 Docker 注册表设置中作为分发层。 E2E Framewo…...
从0开始回顾ElasticSearch
1 elasticsearch概述 1.1 elasticsearch简介 官网: https://www.elastic.co/ ElasticSearch是一个基于Lucene的搜索服务器。它提供了一个分布式多用户能力的全文搜索引擎,基于RESTful web接口。Elasticsearch是用Java开发的,并作为Apache许可条款下的…...

小阿轩yx-Shell编程之条件语句
小阿轩yx-Shell编程之条件语句 条件测试操作 Shell 环境根据命令执行后的返回状态值($?)来判断是否执行成功 返回值 为 0 时:表示成功否则(非 0 值)表示失败或异常 测试工具 test 命令,对特定条件进行…...

MyBatis-Plus 从入门到精通
MyBatis-Plus 从入门到精通 前言快速入门创建一个SpringBoot项目导入依赖配置数据库创建一个实体类创建一个mapper接口在SpringBoot启动类上配置mapper接口的扫描路径在数据库中创建表编写一个SpringBoot测试类 核心功能注解CRUD接口Mapper CRUD接口Service CRUD 接口条件构造器…...
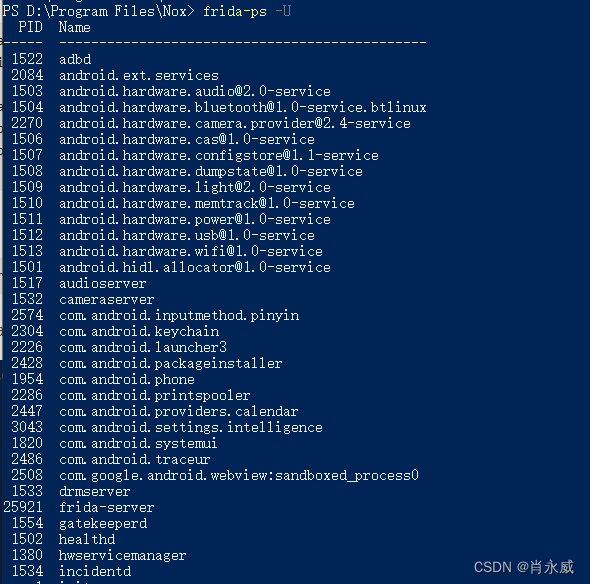
爬虫利器Frida RPC入门——夜神模拟器环境篇
Frida是一款轻量级HOOK框架,可用于多平台上,例如android、windows、ios等。 frida分为两部分,服务端运行在目标机上,通过注入进程的方式来实现劫持应用函数,另一部分运行在系统机器上。frida上层接口支持js、python、…...
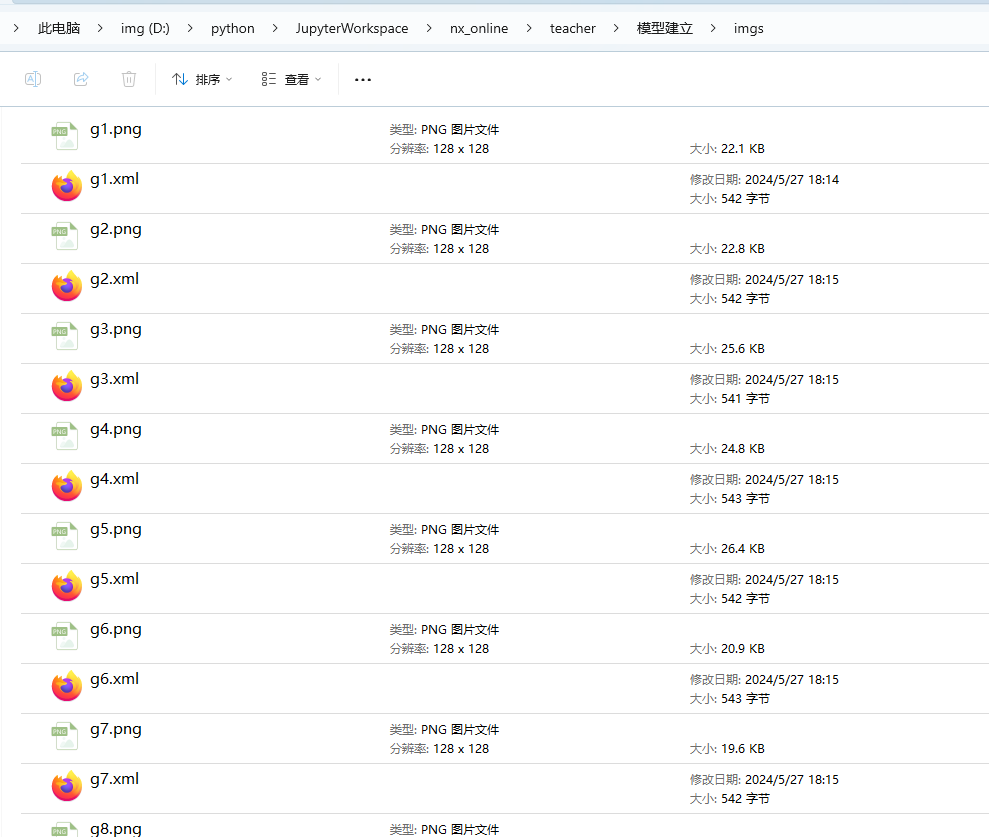
猫狗分类识别模型建立①数据标记
一、labelImg库说明 LabelImg是一款非常流行的图像标注工具,广泛用于机器学习和计算机视觉领域。以下是关于LabelImg的详细介绍: 主要功能和特点 1.图像标注 允许用户在图像中标注物体,选择特定区域,并为这些区域添加标签或类…...

FME学习之旅---day28
我们付出一些成本,时间的或者其他,最终总能收获一些什么。 教程:CSV 入门...

vue3项目中字典和全局方法的创建与使用
在src下新建dict.ts/js,写入下面代码 import { App, Plugin } from vue;interface Dict {auditgrouptypeList: { label: string; value: string }[];auditstateList: { label: string; value: string }[];accountchangeList: { label: string; value: number }[]; }const Dict…...
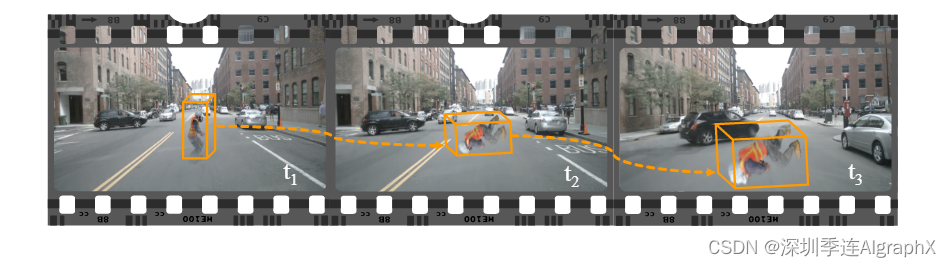
51-54 Sora能制作动作大片还需要一段时间 | DrivingGaussian:周围动态自动驾驶场景的复合高斯飞溅
24年3月,北大、谷歌和加州大学共同发布了DrivingGaussian: Composite Gaussian Splatting for Surrounding Dynamic Autonomous Driving Scenes。视图合成和可控模拟可以生成自动驾驶的极端场景Corner Case,这些安全关键情况有助于以更低成本验证和增强自…...

数据挖掘实战-基于余弦相似度的印度美食推荐系统
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

深入探索DreamFusion:文本到3D生成的革命性技术
深入探索DreamFusion:文本到3D生成的革命性技术 引言: 在人工智能和计算机视觉领域,DreamFusion无疑是一个引人注目的新星。这项技术,基于Google提出的深度学习模型,将自然语言与三维内容生成紧密结合,开…...

JSP期末要点复习
一、JSP工作原理 1.客户端请求JSP页面:用户通过浏览器发送一个请求到服务器,请求一个特定的JSP页面。这个请求被服务器上的Web容器(如Apache Tomcat)接收。 2.JSP转换为Servlet:当JSP页面第一次被请求时࿰…...
)
AJAX(JavaScript版本)
目录 一.AJAX简介 二.XMLHttpRequests对象 2.1XMLHttpRequests对象简介 2.2创建XMLHttpRequests对象 2.3定义回调函数 2.4发送请求 2.5XMLHttpRequests对象方法介绍 2.6XMLHttpRequests对象属性 三.向服务器发送请求 3.1发送请求 3.2使用GET还是POST 3.3使用GET来发…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
