Java(其十二)--集合·初级
ArrayList集合
集合有很多种,ArrayList 是最常用的一种,集合的作用相当于C++中的STL
最显著的特点就是:自动扩容。
一般定义式
ArrayList list = new ArrayList();
//该 list 是可以储存各种类型的数据的,要想约束储存的数据,就需要<>
//导包也是必要的使用前提
//如同C++中的STL一般
约束定义式
ArrayList<String> list = new ArrayList<>();
//如此,只能储存String类型的数据
常用的集合方法

注1:其中的 index 索引是使用的数组的逻辑,即第一个元素的索引是0.
注2:当使用 remove 指定元素值删除,并且该指定值存在重复时,默认删除最靠前的那个元素值。
相关文章:

Java(其十二)--集合·初级
ArrayList集合 集合有很多种,ArrayList 是最常用的一种,集合的作用相当于C中的STL 最显著的特点就是:自动扩容。 一般定义式 ArrayList list new ArrayList(); //该 list 是可以储存各种类型的数据的,要想约束储存的数据&#x…...

疯狂“造人”!美国两党共推新法案,5年培养100万AI及量子人才
当前,全球量子计算人才的短缺已成为制约该领域快速发展的关键瓶颈。 为了解决量子计算人才短缺的问题,各国政府和企业采取了积极措施,加大了对量子教育和培训的投入。根据美国参议院官网消息,2024年5月23日,美国两党议…...

Python 文件操作指南:使用 open 和 with open 实现高效读写
🍀 前言 博客地址: CSDN:https://blog.csdn.net/powerbiubiu 👋 简介 本系列文章主要分享文件操作,了解如何使用 Python 进行文件的读写操作,介绍常见文件格式的读取和写入方法,包括TXT、 CS…...

FasterNet代码阅读
FasterNet 类参数初始化 将图像切分为非重叠的图像块 PatchEmbed 类 将图像分解为非重叠的图像块有以下几个好处: 1. 缩小计算量:对于大尺寸的图像,直接对整个图像进行处理可能会导致计算和内存消耗过大。将图像切分为小块可以降低计算量…...
Rust开源Web框架Salvo源码编译
1.克隆源码: https://github.com/salvo-rs/salvo.git 2.进入salve目录并运行cargo build编译 编译成功 3.编译生成的库 4.安装salve-cli git clone --recursive https://github.com/salvo-rs/salvo-cli.git 编译salve-cli...
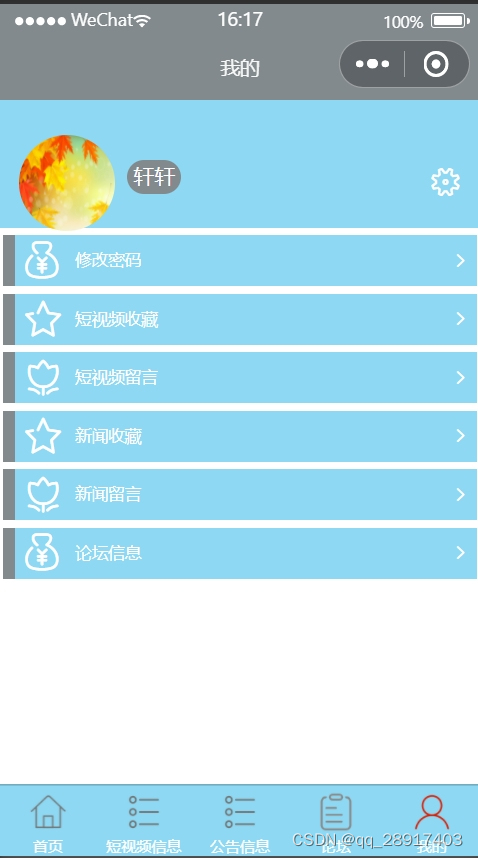
基于Java+SpringBoot+Mybaties-plus+Vue+elememt + uniapp 新闻资讯 的设计与实现
一.项目介绍 本系统分为 后端 和 小程序端 后端:点击登录按钮 设置个人中心、 管理员账号数据维护、 基础数据维护、 短视频信息维护(包括查看短视频留言、短视频收藏)、 论坛维护(增删改查帖子信息,包括查…...
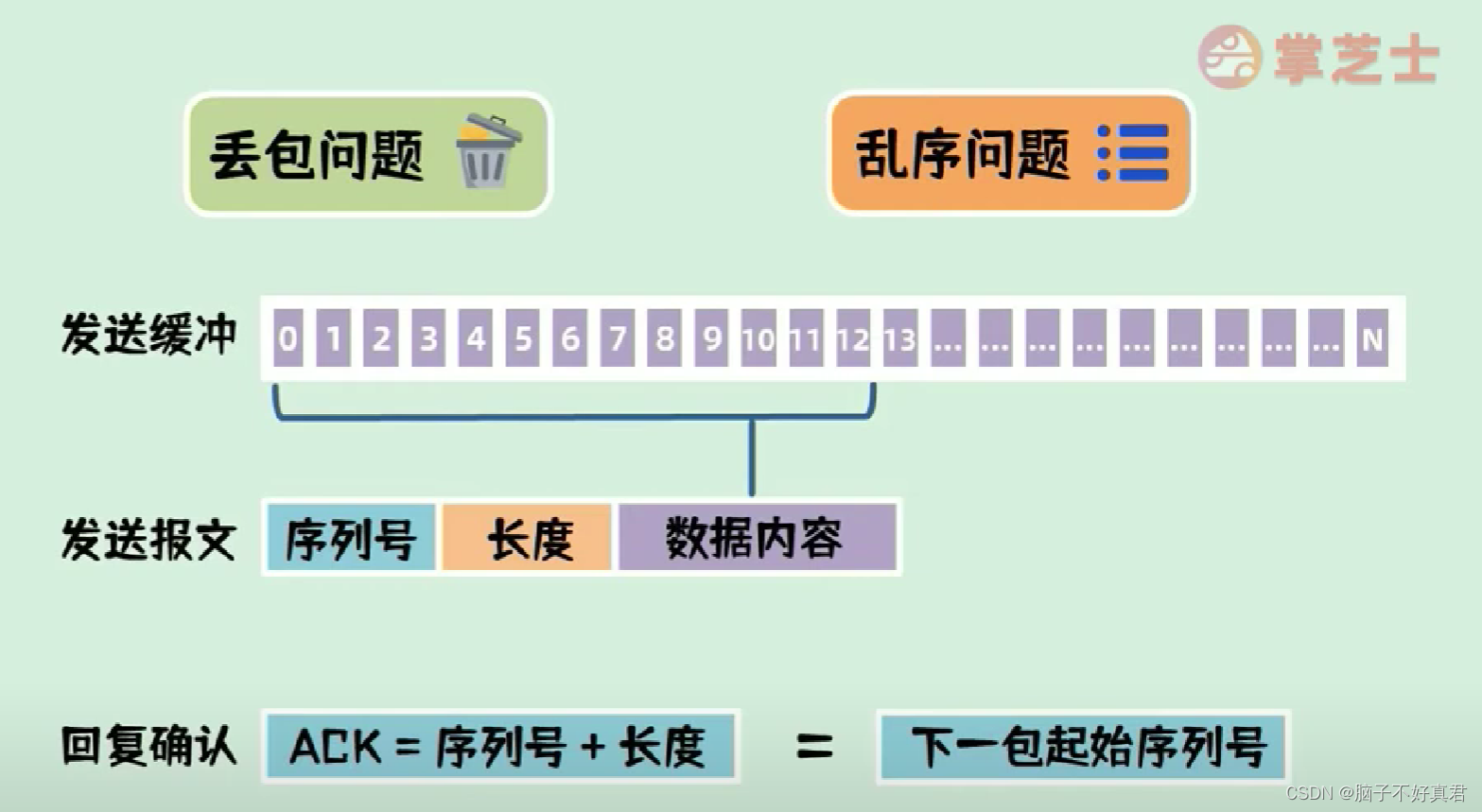
TCP—三次握手和四次挥手
目录 一、三次握手和四次挥手的目的 二、TCP可靠的方面 三、什么是三次握手 四、第三次握手的目的 五、什么是四次挥手 六、超时时间的目的 七、SYN包、ACK包、FIN包 八、解决丢包和乱序 九、参考资料 一、三次握手和四次挥手的目的 TCP三次握手的目的主要是为了确保两…...

基于UDP的网络聊天室
一.项目需求: 如果有用户登录,其他用户可以收到这个人的登录信息如果有人发送信息,其他用户可以收到这个人的群聊信息如果有人下线,其他用户可以收到这个人的下线信息服务器可以发送系统信息 二.服务器端 #include <myhead.h&…...
数组-两个升序数组中位数
一、题目描述 二、解题思路 (一).基本思想: 如果列表总长度allsize( arr1.size()arr2.size() ) 为奇数时,中位数位置应该在两个列表排序后的第 allsize/2 位置处,如果allsize为偶数,中位数应该取 (allsize/2)-1 和 allsize/2 的…...

每日一题《leetcode--116.填充每个结点的下一个右侧结点》
https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/ 题目要求给每个结点的next指针进行填充,使每个结点的next指针指向其下一个右侧结点。如果右侧没有结点,则将next指针设置为空。 struct Node* connect(struct Node* root) {…...
-磁盘结构(5)-Redolog)
【MySQL精通之路】InnoDB(6)-磁盘结构(5)-Redolog
主博客: 【MySQL精通之路】InnoDB(6)-磁盘上的InnoDB结构-CSDN博客 上一篇: 【MySQL精通之路】InnoDB-双写缓冲区-CSDN博客 下一篇: 目录 1.配置Redo Log容量(MySQL 8.0.30或更高版本) 2.配置重做日志容量(MySQL…...

【探索自然语言处理:构建一个简单的文本分类器】
文章目录 前言文本预处理特征提取模型训练文本分类结论 前言 在信息时代,文本数据无处不在,从社交媒体帖子到客户反馈,文本是沟通和信息交流的主要媒介。自然语言处理(NLP)是人工智能的一个分支,它使计算机…...

概率论统计——大数定律
大数定律 弱大数定律(辛钦大数定律) 利用切比雪夫不等式,证明弱大数定律 应用 伯努利大数定理,(辛钦大数定理的推论) 证明伯努利大数定理 注意:这里将二项分布转化成0,1分布来表示,…...

vscode终端命令行前面出现两个conda环境名的问题决解方法
已经安装了conda,打开vscode的terminal时,命令行前面有两个虚拟环境名。 进入vscode的setting 找到Python->Python:Default Interpreter Path,把这个值复位,就可以解决。 如果不想前面带(base),可以运行 conda co…...

“AI黏土人”一夜爆火,图像生成类应用应该如何长期留住用户?
文章目录 最近大火的“AI黏土人”,一股浓浓的《小羊肖恩》风。 凭借这这种搞怪的风格,“AI黏土人”等图像生成类应用凭借其创新技术和市场需求迅速崛起并获得巨大关注。然而,要保持用户黏性并确保长期发展,这些应用需要采取一系列…...
-查询优化(12)-块嵌套循环和批处理Key访问联接)
【MySQL精通之路】SQL优化(1)-查询优化(12)-块嵌套循环和批处理Key访问联接
在MySQL中,可以使用批处理Key访问(BKA)联接算法,该算法使用对联接表的索引访问和联接缓冲区。 BKA算法支持内联接、外联接和半联接操作,包括嵌套的外部联接。 BKA的优点包括由于更高效的表扫描而提高了联接性能。 此…...
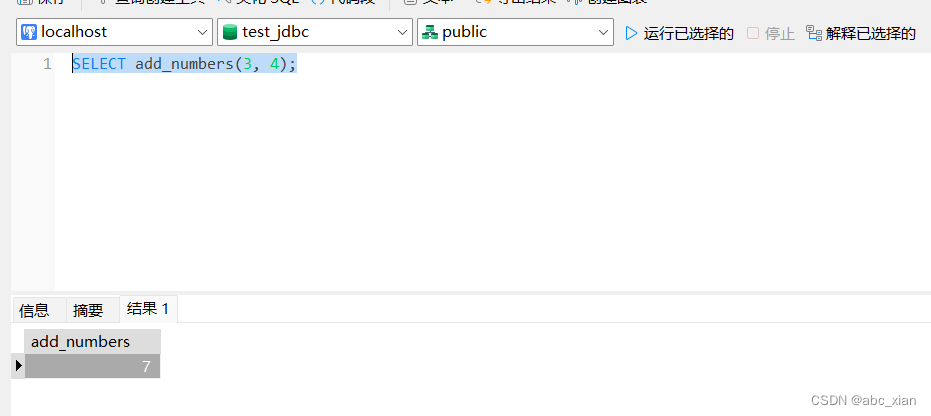
SQL使用函数给多个分表添加同一字段
数据库中分表时,往往需要向多个分表中添加同一个字段,可以定义一个函数,每次调用这个函数向多个份表中添加同意字段。 1、创建函数示例: 在PostgreSQL中创建一个简单的函数 以下是一个在PostgreSQL中创建函数的简单示例&#x…...

OpenAI 再次刷新认知边界:GPT-4 颠覆语音助手市场,流畅度直逼真人互动?
前言 近日,美国人工智能研究公司 OpenAI 发布了其最新旗舰模型 GPT-4o,这一革命性的进展不仅标志着人工智能领域的新突破,更预示着即将步入一个全新的交互时代?GPT-4o 的发布,对于我们来说,意味着人工智能…...
UE5 使用外置摄像头进行拍照并保存到本地
连接外置摄像头功能:https://docs.unrealengine.com/4.27/zh-CN/WorkingWithMedia/IntegratingMedia/MediaFramework/HowTo/UsingWebCams/ 核心功能:UE4 相机拍照功能(图片保存)_ue 移动端保存图片-CSDN博客 思路是: …...
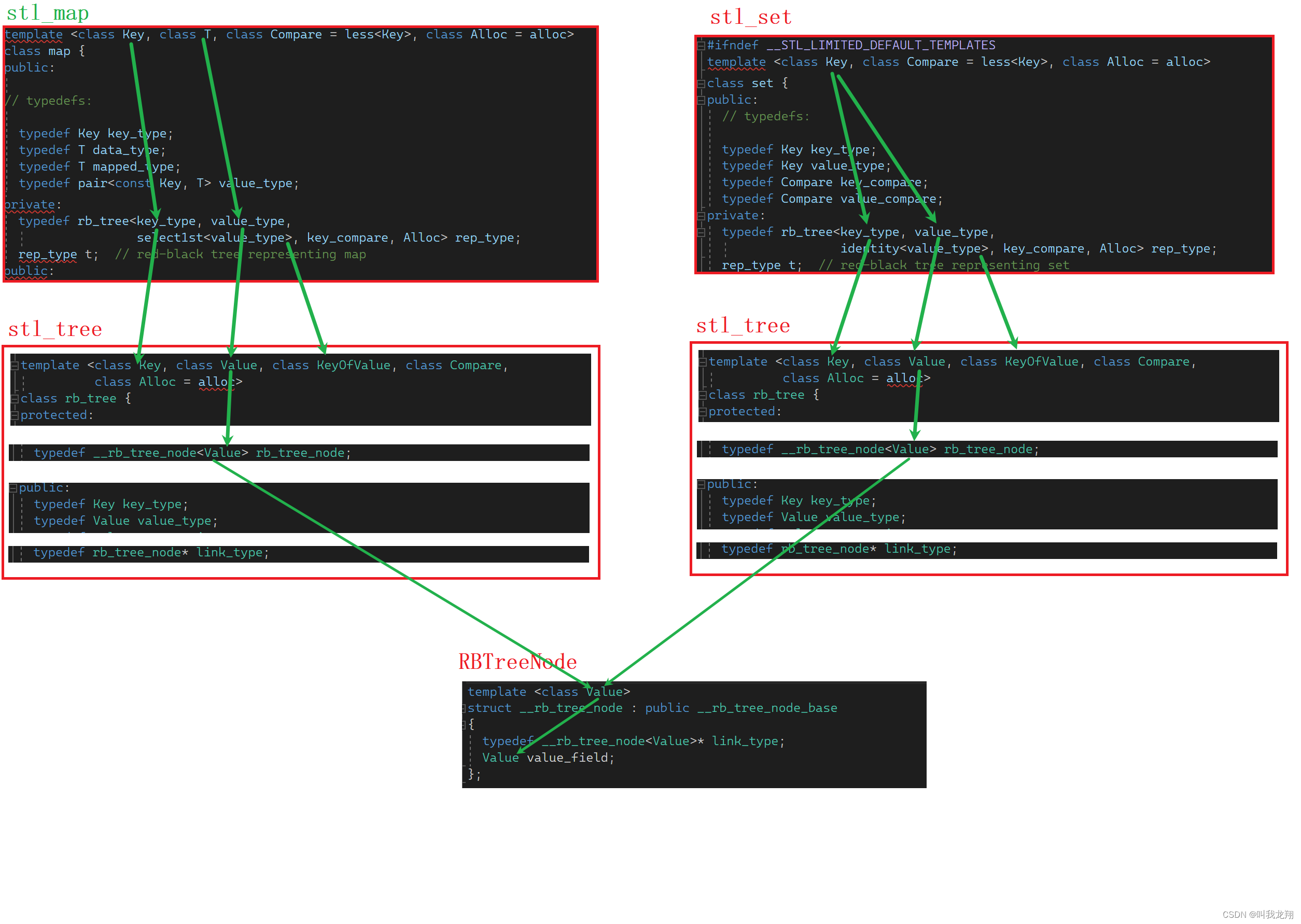
【C++】从零开始map与set的封装
送给大家一句话: 今日的事情,尽心、尽意、尽力去做了,无论成绩如何,都应该高高兴兴地上床恬睡。 – 三毛 《亲爱的三毛》 🌃🌃🌃🌃🌃🌃🌃&#x…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
