数组-两个升序数组中位数
一、题目描述

二、解题思路
(一).基本思想:
如果列表总长度allsize( =arr1.size()+arr2.size() ) 为奇数时,中位数位置应该在两个列表排序后的第 allsize/2 位置处,如果allsize为偶数,中位数应该取 (allsize/2)-1 和 allsize/2 的平均数。
设置两个指针p1、p2,一个指向列表 arr1[0] ,一个指向列表 arr2[0] ,比较两个指针指向列表的值,值较小的指针往后移动一位
再次比较p1、p2,重复上述动作。
(二).注意:因为两个列表长度不一定相同,所以存在某一个指针p1遍历到列表末尾,但是仍然没有找到中位数,这时候中位数有可能就会出现①p1、p2均在列表中间,此时取二者较小值或者平均值、②在另一个列表中、③另一个列表中两个元素取平均值、④p1(此时在末尾)和p2取平均值、⑤p1(此时在末尾)这几种情况,下面就对各种可能出现的情况进行举例说明,以写出比较严谨的代码实现,覆盖各种可能出现的情况。
比较次数和总列表长度的奇偶性还有确定中位数位置是有关联性的,这一点可以自己在下面例子里尝试一下。
1.当allsize为奇数时:只存在一个中位数,此时比较次数为 allsize/2 次
(1).p1、p2在中间位置
[1,2,3,8,9] 和 [4,5,6,7] ,总列表 [1,2,3,4,5,6,7,8,9]
总长度为9,比较4次:
第一次 p1->1,p2->4,p1<p2,p1++;
第二次 p1->2,p2->4,p1<p2,p1++;
第三次 p1->3,p2->4,p1<p2,p1++;
第四次 p1->8,p2->4,p1>p2,p2++;
此时:p1->8,p2->5 取二者较小值为5,中位数为5
(2).p1在arr1末尾,并且p1<=p2时
[1,2,3,4]和[5,6,7,8,9],总列表 [1,2,3,4,5,6,7,8,9]
总长度为9,比较4次:
第一次 p1->1,p2->5,p1<p2,p1++;
第二次 p1->2,p2->5,p1<p2,p1++;
第三次 p1->3,p2->5,p1<p2,p1++;
第四次 p1->4,p2->5,p1<p2,此时p1已经在末尾,不再++,设置变量标记中位数在arr2中(p2侧);
此时:直接取p2为中位数,中位数为5
(3).p1在arr1末尾,并且p1>p2时
[1,2,3,5]和[4,6,7,8,9],总列表 [1,2,3,4,5,6,7,8,9]
总长度为9,比较4次:
第一次 p1->1,p2->4,p1<p2,p1++;
第二次 p1->2,p2->4,p1<p2,p1++;
第三次 p1->3,p2->4,p1<p2,p1++;
第四次 p1->5,p2->4,p1>p2,此时p2++;
此时:p1->5,p2->6 取p1、p2二者较小值,中位数为5
2.当allsize为偶数时,中位数等于中间两个元素取平均值,此时两个元素比较次数为 allsize/2 -1 次,执行完allsize/2 -1 次判断时:
(1).p1、p2在中间位置,并不能确定中间两个数在哪一侧产生,可能是两侧各贡献一个(包括p1或者p2没有发生移动的情况)
两侧各贡献一个:
(这种情况牛客里面的测试用例没有覆盖这种情况,刚开始我写的代码这部分有缺陷,所以会出现问题,下面的代码实现已经补上了处理策略,判断过程看下面加粗黄色说明部分)
[1,2,3,8,9] 和 [4,5,6,7,10] ,总列表 [1,2,3,4,5,6,7,8,9,10]
总长度为10,比较4次:
第一次 p1->1,p2->4,p1<p2,p1++;
第二次 p1->2,p2->4,p1<p2,p1++;
第三次 p1->3,p2->4,p1<p2,p1++;
第四次 p1->8,p2->4,p1>p2,p2++;
此时:p1->8,p2->5,最后一次移动的是p2(作为求平均数的左值),且p2未到达末尾,需要比较(p2+1)和p1位置的值,(p2+1)->6,p1->8,取二者较小值为6,中位数为(5+6)/2=5.5
[4,5,6,7,10] 和 [1,2,3,8,9] ,总列表 [1,2,3,4,5,6,7,8,9,10]
总长度为10,比较4次:
第一次 p2->4,p1->1,p1>p2,p2++;
第二次 p1->4,p2->2,p1>p2,p2++;
第三次 p1->4,p2->3,p1>p2,p2++;
第四次 p1->4,p2->8,p1<p2,p1++;
此时:p1->5,p2->8,最后一次移动的是p1(作为求平均数的左值),且p1未到达末尾,需要比较(p1+1)和p2位置的值,(p1+1)->6,p1->8,取二者较小值为6,中位数为(5+6)/2=5.5
p1或者p2没有发生移动的情况:
[1,2,3,7]和[4,5,8,9],总列表 [1,2,3,4,5,7,8,9]
总长度为8,比较3次:
第一次 p1->1,p2->4,p1<p2,p1++;
第二次 p1->2,p2->4,p1<p2,p1++;
第三次 p1->3,p2->4,p1<p2,p1++;
此时:p1->7,p2->4 需要比较一下p1和p2+1位置的大小,如果p1>p2+1,中位数选择p2和p2+1位置元素和的平均值;如果p1<p2+1,中位数选择p1和p2的平均值。
[4,5,8,9] 和 [1,2,3,7],总列表 [1,2,3,4,5,7,8,9]
总长度为8,比较3次:
第一次 p1->4,p2->1,p1>p2,p2++;
第二次 p1->4,p2->2,p1>p2,p2++;
第三次 p1->4,p2->3,p1>p2,p2++;
此时:p1->4,p2->7 需要比较一下p2和p1+1位置的大小,如果p2>p1+1,中位数选择p1和p1+1位置元素和的平均值;如果p2<p1+1,中位数选择p1和p2的平均值。
并不能确定是否只出现在一侧的情况:
[1,8] 和 [4,5,6,7,8,9],总列表 [1,4,5,6,7,8,8,9]
总长度为8,比较3次:
第一次 p1->1,p2->4,p1<p2,p1++;
第二次 p1->8到达末尾,p2->4,p1>p2,p2++;
第三次 p1->8到达末尾,p2->5,p1>p2,p2++;
此时:p1->8,p2->6 p1到达末尾,p2一定是中间两个数之一,需要比较一下p2+1和p1的大小,取较小值作为另一个数,p2+1->7,p1->8,取p2+1和p2的平均数作为中位数,值为6.5。
(2).p1早已到达arr1末尾,确定两个数确定在p2侧产生
[6,7] 和 [5,9,10,11,12,13],总列表 [5,6,7,9,10,11,12,13]
总长度为8,比较3次:
第一次 p1->6,p2->5,p1>p2,p2++;
第二次 p1->6,p2->9,p1<p2,p1++;
第三次 p1->7到达末尾,p2->9,p1<p2,p2++,且设置标志位;
此时:中间两个数只会是p2和p2+1位置的值,计算两个数的平均数:p2->9,(p2+1)->10,平均值为8.5。
(3).p2早已到达arr2末尾,中间两个数确定在p1侧产生,这个执行过程大家自己根据上面(2)的过程推理一下。
[5,9,10,11,12,13] 和 [6,7],总列表 [5,6,7,9,10,11,12,13]
三、代码实现
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param nums1 int整型ArrayList* @param nums2 int整型ArrayList* @return double浮点型*/public double Median (ArrayList<Integer> nums1, ArrayList<Integer> nums2) {double res = 0;int allsize = nums1.size() + nums2.size();int mididx = allsize / 2;int icounter=0;boolean oddnum=false;//奇数数if(allsize%2!=0){oddnum=true;//此时根据side判断取哪一侧的值,如果没有出现倾斜情况,则取p1、p2较小值icounter=mididx;}else{oddnum=false;//此时取p1和p2位置平均值icounter=mididx-1;}int p1 = 0, p2 = 0;boolean p1side=false,p2side=false;int lastestmove=0;while (icounter > 0) {if (p1 < (nums1.size() - 1) && nums1.get(p1) <= nums2.get(p2)) {p1++;lastestmove=1;}else if(p1 == (nums1.size() - 1)){if(!oddnum){if(!p2side&&nums1.get(p1)>nums2.get(p2)){p2++;lastestmove=2;}else if(!p2side&&nums1.get(p1)<=nums2.get(p2)){p2side=true;}else{p2++;lastestmove=2;} }else{if(!p2side&&nums1.get(p1)>nums2.get(p2)){p2++;lastestmove=2;}else{if(!p2side){p2side=true;}else{p2++;lastestmove=2;}}}}else if (p2 < (nums2.size() - 1) && nums1.get(p1) > nums2.get(p2)) {p2++;lastestmove=2;}else if (p2 == (nums2.size() - 1)) {if(!oddnum){if(!p1side&&nums2.get(p2)>=nums1.get(p1)){p1++;lastestmove=1;}else if(!p1side&&nums2.get(p2)<nums1.get(p1)){p1side=true;}else{p1++;lastestmove=1;} }else{if(!p1side&&nums2.get(p2)>nums1.get(p1)){p1++;lastestmove=1;}else{if(!p1side){p1side=true;}else{p1++;lastestmove=1;}}}}icounter--;}if (!oddnum) { //此时取中间两个值的平均数为中位数if(p1side){//中间两个数位于p1侧res=((double)(nums1.get(p1)) + (double)(nums1.get(p1+1))) / 2;}else if(p2side){//中间两个数位于p2侧res=((double)(nums2.get(p2)) + (double)(nums2.get(p2+1))) / 2;}else{double minright=(double)(nums2.get(p2));double minleft=(double)(nums1.get(p1));if(lastestmove==1){//此时p1为左值//偶数个数时,当最后一次移动发生在p1侧且p1侧没有到达末尾,比较p1+1和p2大小,取较小值作为右值minleft=(double)(nums1.get(p1));minright=nums1.get(p1+1)>nums2.get(p2)?nums2.get(p2):nums1.get(p1+1);}else if(lastestmove==2){//此时p2为右值//原理同上,比较p2+1和p1大小,取较小值minleft=(double)(nums2.get(p2));minright=nums2.get(p2+1)>nums1.get(p1)?nums1.get(p1):nums2.get(p2+1);}res=( minleft + minright) / 2;}} else { //此时取p1、p2两者较小的值if(p1side){res = nums1.get(p1);}else if(p2side){res = nums2.get(p2);}else{res = Math.min(nums2.get(p2),nums1.get(p1));}}return res;}
}四、刷题链接
两个升序数组的中位数_牛客题霸_牛客网
五、近似题目
数组-在两个长度相等的有序数组中找到上中位数-CSDN博客文章浏览阅读272次,点赞4次,收藏6次。java刷题:查找两个长度相等的有序数组中的上中位数。https://blog.csdn.net/hehe_soft_engineer/article/details/139200124?spm=1001.2014.3001.5502
相关文章:
数组-两个升序数组中位数
一、题目描述 二、解题思路 (一).基本思想: 如果列表总长度allsize( arr1.size()arr2.size() ) 为奇数时,中位数位置应该在两个列表排序后的第 allsize/2 位置处,如果allsize为偶数,中位数应该取 (allsize/2)-1 和 allsize/2 的…...

每日一题《leetcode--116.填充每个结点的下一个右侧结点》
https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/ 题目要求给每个结点的next指针进行填充,使每个结点的next指针指向其下一个右侧结点。如果右侧没有结点,则将next指针设置为空。 struct Node* connect(struct Node* root) {…...
-磁盘结构(5)-Redolog)
【MySQL精通之路】InnoDB(6)-磁盘结构(5)-Redolog
主博客: 【MySQL精通之路】InnoDB(6)-磁盘上的InnoDB结构-CSDN博客 上一篇: 【MySQL精通之路】InnoDB-双写缓冲区-CSDN博客 下一篇: 目录 1.配置Redo Log容量(MySQL 8.0.30或更高版本) 2.配置重做日志容量(MySQL…...

【探索自然语言处理:构建一个简单的文本分类器】
文章目录 前言文本预处理特征提取模型训练文本分类结论 前言 在信息时代,文本数据无处不在,从社交媒体帖子到客户反馈,文本是沟通和信息交流的主要媒介。自然语言处理(NLP)是人工智能的一个分支,它使计算机…...

概率论统计——大数定律
大数定律 弱大数定律(辛钦大数定律) 利用切比雪夫不等式,证明弱大数定律 应用 伯努利大数定理,(辛钦大数定理的推论) 证明伯努利大数定理 注意:这里将二项分布转化成0,1分布来表示,…...

vscode终端命令行前面出现两个conda环境名的问题决解方法
已经安装了conda,打开vscode的terminal时,命令行前面有两个虚拟环境名。 进入vscode的setting 找到Python->Python:Default Interpreter Path,把这个值复位,就可以解决。 如果不想前面带(base),可以运行 conda co…...

“AI黏土人”一夜爆火,图像生成类应用应该如何长期留住用户?
文章目录 最近大火的“AI黏土人”,一股浓浓的《小羊肖恩》风。 凭借这这种搞怪的风格,“AI黏土人”等图像生成类应用凭借其创新技术和市场需求迅速崛起并获得巨大关注。然而,要保持用户黏性并确保长期发展,这些应用需要采取一系列…...
-查询优化(12)-块嵌套循环和批处理Key访问联接)
【MySQL精通之路】SQL优化(1)-查询优化(12)-块嵌套循环和批处理Key访问联接
在MySQL中,可以使用批处理Key访问(BKA)联接算法,该算法使用对联接表的索引访问和联接缓冲区。 BKA算法支持内联接、外联接和半联接操作,包括嵌套的外部联接。 BKA的优点包括由于更高效的表扫描而提高了联接性能。 此…...
SQL使用函数给多个分表添加同一字段
数据库中分表时,往往需要向多个分表中添加同一个字段,可以定义一个函数,每次调用这个函数向多个份表中添加同意字段。 1、创建函数示例: 在PostgreSQL中创建一个简单的函数 以下是一个在PostgreSQL中创建函数的简单示例&#x…...

OpenAI 再次刷新认知边界:GPT-4 颠覆语音助手市场,流畅度直逼真人互动?
前言 近日,美国人工智能研究公司 OpenAI 发布了其最新旗舰模型 GPT-4o,这一革命性的进展不仅标志着人工智能领域的新突破,更预示着即将步入一个全新的交互时代?GPT-4o 的发布,对于我们来说,意味着人工智能…...
UE5 使用外置摄像头进行拍照并保存到本地
连接外置摄像头功能:https://docs.unrealengine.com/4.27/zh-CN/WorkingWithMedia/IntegratingMedia/MediaFramework/HowTo/UsingWebCams/ 核心功能:UE4 相机拍照功能(图片保存)_ue 移动端保存图片-CSDN博客 思路是: …...
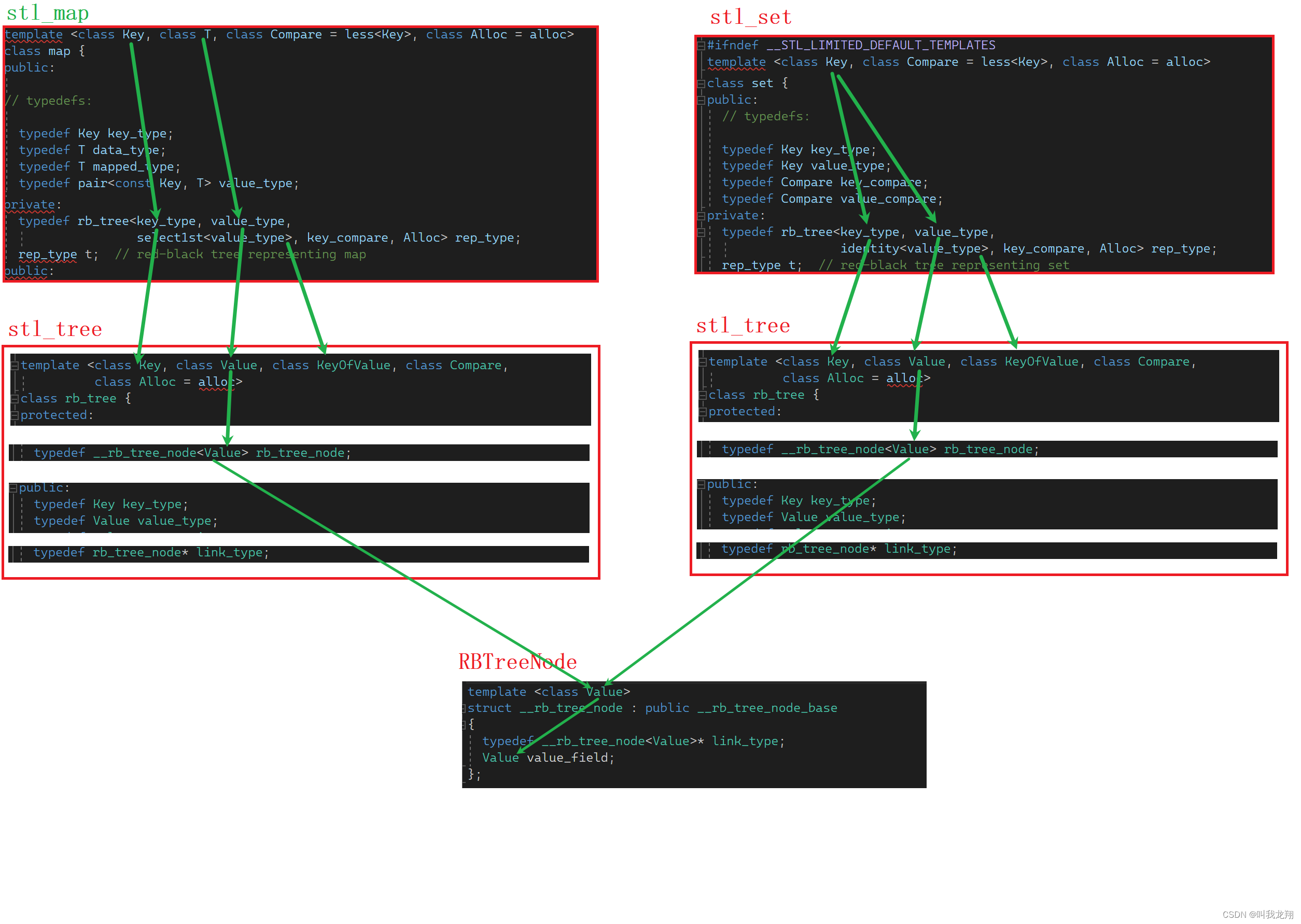
【C++】从零开始map与set的封装
送给大家一句话: 今日的事情,尽心、尽意、尽力去做了,无论成绩如何,都应该高高兴兴地上床恬睡。 – 三毛 《亲爱的三毛》 🌃🌃🌃🌃🌃🌃🌃&#x…...

Python可以声明并赋值一个hash类型变量吗?
在Python中,不能直接声明一个变量为hash类型,因为Python是一种动态类型语言,不需要(也不能)在声明变量时指定其类型。变量的类型是根据赋给它的值自动推断的。 将一个哈希值(即一个整数)赋值给…...

苗情灾情监控系统—提高农业生产效率
TH-MQ2苗情灾情监控系统是一种用于监测农作物生长状况和灾情的设备,通过实时监测和数据分析,帮助农民及时了解作物生长情况,采取相应的管理措施,提高农业生产效率和降低生产成本。 该系统通常由多种传感器、摄像头、数据传输模块等…...

wpf自定义按钮样式
在WPF中,自定义按钮样式可以通过创建一个ControlTemplate来实现。以下是一个简单的自定义按钮样式的例子: 首先,在你的WPF项目资源字典中定义按钮的ControlTemplate。 <Window.Resources><ControlTemplate x:Key"CustomButto…...

Meme币总市值突破630亿美元 以太坊ETF获批意味着代币化资产“完全安全”
近日,数字货币市场再次掀起轩然大波。一方面,Meme币总市值突破了630亿美元,令人瞠目结舌;另一方面,以太坊ETF的获批也引发了市场的广泛关注,被视为代币化资产的“完全安全”标志。 Meme币总市值飙升 Meme币…...
MySQL数据库语法(二)
一、数据库的创建 创建数据库CRATE DATABASE语法:CREATE DATABASE [IF NOT EXISTS]数据库名;功能:用给定的名字创建一个数据库如果数据库已经存在,发生一个错误。查看创建数据库:SHOW CREATE DATABASE <数据库名>ÿ…...

Linux makefile
Linux makefile 用makefile去自动编译和删除静态库和动态库 在实际开发中,项目的源代码文件比较多,按类型、功能、模块分别存放在不同的目录和文件中,哪些文件需要先编译,那些文件后编译,那些文件需要重新编译…...

信息安全基础知识
信息安全基础知识 安全策略表达模型是一种对安全需求与安全策略的抽象概念表达,一般分为自主访问控制模型(HRU)和强制访问控制模型(BLP、Biba)IDS基本原理是通过分析网络行为(访问方式、访问量、与历史访问…...
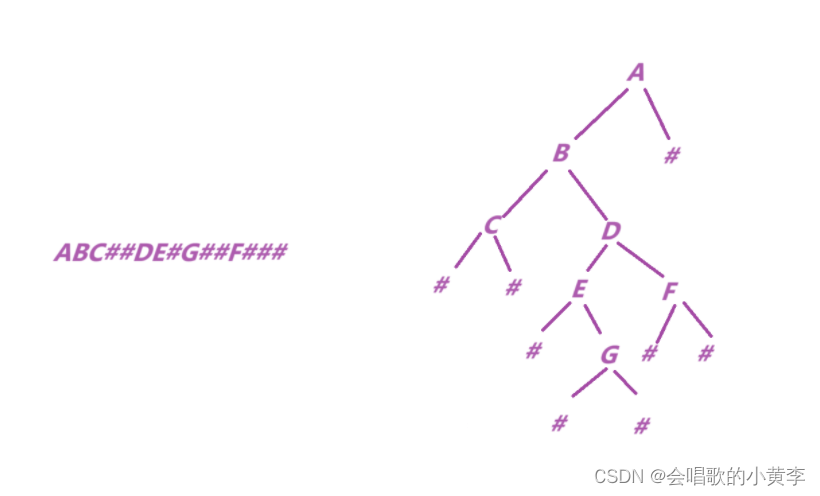
【数据结构】链式二叉树(超详细)
文章目录 前言二叉树的链式结构二叉树的遍历方式二叉树的深度优先遍历前序遍历(先根遍历)中序遍历(中根遍历)后序遍历(后根遍历) 二叉树的广度优先遍历层序遍历 二叉树链式结构接口实现二叉树结点个数二叉树叶子结点个数二叉树的深度(高度)二叉树第k层结…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
