Borel-Cantelli 引理
翻译自大佬
https://huarui1998.com/Notes/math/borel-cantelli.html
1. 集序列的 lim inf \lim\inf liminf 和 lim sup \lim\sup limsup
类似于定义实数序列 { a k } \{a_k\} {ak} 的 lim inf \lim\inf liminf 和 lim sup \lim\sup limsup,
lim inf k → ∞ a k = sup n ≥ 1 ( inf k ≥ n a k ) , lim sup k → ∞ a k = inf n ≥ 1 ( sup k ≥ n a k ) , \liminf\limits_{k\to\infty}a_k = \sup_{n\geq 1}(\inf_{k\geq n} a_k),\quad \limsup\limits_{k\to\infty}a_k = \inf_{n\geq 1}(\sup_{k\geq n} a_k), k→∞liminfak=n≥1sup(k≥ninfak),k→∞limsupak=n≥1inf(k≥nsupak),
我们也可以定义集序列 { A k } \{A_k\} {Ak} 的 lim inf \lim\inf liminf 和 lim sup \lim\sup limsup,
只需将 inf \inf inf 替换为 ∩ \cap ∩,将 sup \sup sup 替换为 ∪ \cup ∪,即
lim inf k → ∞ A k = ⋃ n ≥ 1 ⋂ k ≥ n A k , lim sup k → ∞ A k = ⋂ n ≥ 1 ⋃ k ≥ n A k . \liminf\limits_{k\to\infty}A_k = \bigcup_{n\geq 1}\bigcap_{k\geq n} A_k,\quad \limsup\limits_{k\to\infty}A_k = \bigcap_{n\geq 1}\bigcup_{k\geq n} A_k. k→∞liminfAk=n≥1⋃k≥n⋂Ak,k→∞limsupAk=n≥1⋂k≥n⋃Ak.
根据德摩根定律,我们有
( lim sup k → ∞ A k ) c = ( ⋂ n ≥ 1 ⋃ k ≥ n A k ) c = ⋃ n ≥ 1 ( ⋃ k ≥ n A k ) c = ⋃ n ≥ 1 ⋂ k ≥ n A k c = lim inf k → ∞ A k c . (1) \left(\limsup\limits_{k\to\infty}A_k\right)^c = \left(\bigcap_{n\geq 1}\bigcup_{k\geq n} A_k\right)^c = \bigcup_{n\geq 1}\left(\bigcup_{k\geq n} A_k\right)^c = \bigcup_{n\geq 1}\bigcap_{k\geq n} A_k^c =\liminf\limits_{k\to\infty}A_k^c.\tag{1} (k→∞limsupAk)c=(n≥1⋂k≥n⋃Ak)c=n≥1⋃(k≥n⋃Ak)c=n≥1⋃k≥n⋂Akc=k→∞liminfAkc.(1)
这两个符号有两个重要性质。
定理
- a ∈ lim inf k A k a\in \lim \inf \limits_k A_k a∈limkinfAk 当且仅当存在一个整数 N N N 使得 a ∈ A n a\in A_n a∈An 对所有 n ≥ N n\geq N n≥N 成立。
- a ∈ lim sup k A k a\in\lim \sup \limits_kA_k a∈limksupAk 当且仅当 a a a 属于 { A k } \{A_k\} {Ak} 的无穷多个项。
证明
首先,如果 a ∈ lim inf k A k a\in\liminf_kA_k a∈liminfkAk,这意味着 a a a 属于 { ∩ k ≥ n A k : n ≥ 1 } \{\cap_{k\geq n}A_k:n\geq 1\} {∩k≥nAk:n≥1} 中的至少一个,假设 a ∈ ∩ k ≥ N A k a\in \cap_{k\geq N}A_k a∈∩k≥NAk,
那么 a ∈ A k a\in A_k a∈Ak 对所有 k ≥ N k\geq N k≥N 成立。
其次,如果 a ∈ lim sup k A k a\in\limsup_kA_k a∈limsupkAk,这意味着 a a a 属于 { ∪ k ≥ n A k : n ≥ 1 } \{\cup_{k\geq n}A_k:n\geq 1\} {∪k≥nAk:n≥1} 的所有。
假设 a a a 只属于 { A k } \{A_k\} {Ak} 的有限项,例如 { A k 1 , ⋯ , A k m } \{A_{k_1},\cdots,A_{k_m}\} {Ak1,⋯,Akm},那么令 M = max { k 1 , ⋯ , k m } M = \max\{k_1,\cdots,k_m\} M=max{k1,⋯,km},我们有
a ∉ A k a\notin A_k a∈/Ak 对所有 k ≥ M + 1 k\geq M+1 k≥M+1 成立,即 a ∉ ∪ k ≥ M + 1 A k a\notin \cup_{k\geq M+1}A_k a∈/∪k≥M+1Ak,这导致矛盾。
■ \tag*{$\blacksquare$} ■
由于上述定理,有时我们说事件 A k A_k Ak ( k = 1 , 2 , ⋯ k=1,2,\cdots k=1,2,⋯) 无穷次发生,如果事件 lim sup k A k \limsup_kA_k limsupkAk 发生,或简称为 A k A_k Ak i.o.。
定理
如果每个 A k A_k Ak 是一个事件(即 ∈ F \in\cal F ∈F),我们有
- P ( lim inf k → ∞ A k ) = lim n → ∞ P ( ⋂ k ≥ n A k ) (2) \mathbb{P} (\liminf\limits_{k\to\infty}A_k)=\lim_{n\to\infty}\mathbb{P}(\bigcap_{k\geq n}A_k)\tag{2} P(k→∞liminfAk)=n→∞limP(k≥n⋂Ak)(2)
- P ( lim sup k → ∞ A k ) = lim n → ∞ P ( ⋃ k ≥ n A k ) (3) \mathbb{P}(\limsup\limits_{k\to\infty}A_k)=\lim_{n\to\infty}\mathbb{P}(\bigcup_{k\geq n}A_k)\tag{3} P(k→∞limsupAk)=n→∞limP(k≥n⋃Ak)(3)
证明
记
F n = ⋂ k ≥ n A k , F_n = \bigcap_{k\geq n}A_k, Fn=k≥n⋂Ak,
那么 { F n } \{F_n\} {Fn} 是一个递增序列,即 F 1 ⊆ F 2 ⊆ F 3 ⋯ F_1\subseteq F_2 \subseteq F_3\cdots F1⊆F2⊆F3⋯,根据概率测度的连续性,我们有
P ( ⋃ n F n ) = lim n → ∞ P ( F n ) , \mathbb{P}(\bigcup_{n}F_n) = \lim_{n\to\infty}\mathbb{P}(F_n), P(n⋃Fn)=n→∞limP(Fn),
因此 (2) 成立。 (3) 也直接由 (1) 和 (2) 得出。
■ \tag*{$\blacksquare$} ■
2. 第一 Borel-Cantelli 引理
定理(Borel-Cantelli)
假设 { A k } \{A_k\} {Ak} 是事件,如果
∑ k P ( A k ) < ∞ , \sum_k\mathbb{P}(A_k)\lt\infty, k∑P(Ak)<∞,
那么我们有 P ( A k i.o. ) = 0. \mathbb{P}(A_k\;\text{i.o.})=0. P(Aki.o.)=0.
证明
记 B n B_n Bn 为 B n = ⋃ k ≥ n A k , B_n = \bigcup_{k\geq n} A_k, Bn=k≥n⋃Ak,
根据 (3) 我们有
P ( A k i.o. ) = P ( lim sup k → ∞ A k ) = lim n → ∞ P ( B n ) . \mathbb{P}(A_k\;\text{i.o.}) = \mathbb{P}(\limsup\limits_{k\to\infty}A_k)=\lim_{n\to\infty}\mathbb{P}(B_n). P(Aki.o.)=P(k→∞limsupAk)=n→∞limP(Bn).
我们只需要证明 P ( B n ) → 0 \mathbb{P}(B_n)\to 0 P(Bn)→0。
由于概率测度的次可加性,我们有
P ( B n ) = P ( ⋃ k ≥ n A k ) ≤ ∑ k = n ∞ P ( A k ) = ∑ k = 1 ∞ P ( A k ) − ∑ k = 1 n − 1 P ( A k ) → 0 , \mathbb{P}(B_n) = \mathbb{P}(\bigcup_{k\geq n} A_k)\leq \sum_{k=n}^\infty \mathbb{P}(A_k)=\sum_{k=1}^\infty \mathbb{P}(A_k) -\sum_{k=1}^{n-1} \mathbb{P}(A_k)\to 0, P(Bn)=P(k≥n⋃Ak)≤k=n∑∞P(Ak)=k=1∑∞P(Ak)−k=1∑n−1P(Ak)→0,
当 n → ∞ n\to \infty n→∞ 时,收敛性由
∑ k = 1 ∞ P ( A k ) < ∞ \sum_{k=1}^\infty \mathbb{P}(A_k)\lt\infty k=1∑∞P(Ak)<∞ 保证。
■ \tag*{$\blacksquare$} ■
3. 第二 Borel-Cantelli 引理
定理(Borel-Cantelli)
假设 { A k } \{A_k\} {Ak} 是独立事件,如果
∑ k P ( A k ) = ∞ , \sum_k\mathbb{P}(A_k)=\infty, k∑P(Ak)=∞,
那么我们有 P ( A k i.o. ) = 1. \mathbb{P}(A_k\;\text{i.o.})=1. P(Aki.o.)=1.
证明
根据(1),我们有:
P ( A k i.o. ) = P ( lim sup k → ∞ A k ) = 1 − P ( lim inf k → ∞ A k c ) = 1 − lim n → ∞ P ( ⋂ k ≥ n A k c ) (根据 (2)) = 1 − lim n → ∞ ∏ k = n ∞ P ( A k c ) (由于独立性) = 1 − lim n → ∞ ∏ k = n ∞ ( 1 − P ( A k ) ) ≥ 1 − lim n → ∞ ∏ k = n ∞ exp ( − P ( A k ) ) (因为 1 − x ≤ e − x ) = 1 − lim n → ∞ exp ( − ∑ k = n ∞ P ( A k ) ) = 1 (因为对于任何 n , ∑ k = n ∞ P ( A k ) = ∞ ) \begin{align*} \mathbb{P}(A_k\;\text{i.o.}) &= \mathbb{P}(\limsup_{k \to \infty} A_k) \\ &= 1 - \mathbb{P}(\liminf_{k \to \infty} A_k^c) \\ &= 1 - \lim_{n \to \infty} \mathbb{P}\left(\bigcap_{k \geq n} A_k^c\right) & \text{(根据 (2))} \\ &= 1 - \lim_{n \to \infty} \prod_{k = n}^\infty \mathbb{P}(A_k^c) & \text{(由于独立性)} \\ &= 1 - \lim_{n \to \infty} \prod_{k = n}^\infty (1 - \mathbb{P}(A_k)) \\ &\geq 1 - \lim_{n \to \infty} \prod_{k = n}^\infty \exp(-\mathbb{P}(A_k)) & \text{(因为 $1 - x \leq e^{-x}$)} \\ &= 1 - \lim_{n \to \infty} \exp\left(-\sum_{k = n}^\infty \mathbb{P}(A_k)\right) \\ &= 1 & \text{(因为对于任何 $n$,$\sum_{k = n}^\infty \mathbb{P}(A_k) = \infty$)} \end{align*} P(Aki.o.)=P(k→∞limsupAk)=1−P(k→∞liminfAkc)=1−n→∞limP(k≥n⋂Akc)=1−n→∞limk=n∏∞P(Akc)=1−n→∞limk=n∏∞(1−P(Ak))≥1−n→∞limk=n∏∞exp(−P(Ak))=1−n→∞limexp(−k=n∑∞P(Ak))=1(根据 (2))(由于独立性)(因为 1−x≤e−x)(因为对于任何 n,∑k=n∞P(Ak)=∞)
\tag*{ ■ \blacksquare ■}
我们可以通过将“独立”替换为一个更弱的条件“成对独立”来增强第二 Borel-Cantelli 引理。
定理(成对独立版本 Borel-Cantelli 引理)
假设 { A k } \{A_k\} {Ak} 是成对独立事件,如果
∑ k P ( A k ) = ∞ , \sum_k\mathbb{P}(A_k)=\infty, k∑P(Ak)=∞,
那么我们有 P ( A k i.o. ) = 1. \mathbb{P}(A_k\;\text{i.o.})=1. P(Aki.o.)=1.
证明
设 I k \mathbb{I}_{k} Ik 为 A k A_k Ak 的指示函数,则 E ( I k ) = P ( A k ) \mathbb{E}(\mathbb{I}_k) = \mathbb{P}(A_k) E(Ik)=P(Ak)。设 S n S_n Sn 为 I k \mathbb{I}_k Ik 的部分和,即
S n = ∑ k = 1 n I k , S_n = \sum^n_{k=1} \mathbb{I}_k, Sn=k=1∑nIk,
记
S = lim n → ∞ S n = ∑ k = 1 ∞ I k . S = \lim_{n\to \infty} S_n = \sum^\infty_{k=1} \mathbb{I}_k. S=n→∞limSn=k=1∑∞Ik.
那么 ∑ k P ( A k ) = ∞ \sum_k\mathbb{P}(A_k) = \infty ∑kP(Ak)=∞ 意味着
E ( S ) = ∞ . \mathbb{E}(S) = \infty. E(S)=∞.
而 x ∈ A k i.o. x \in A_k \;\text{i.o.} x∈Aki.o. 等价于
S ( x ) = ∑ k = 1 ∞ I k ( x ) = ∞ , S(x) = \sum^\infty_{k=1}\mathbb{I}_k(x) = \infty, S(x)=k=1∑∞Ik(x)=∞,
因此我们的目标是证明 P ( S = ∞ ) = 1 \mathbb{P}(S=\infty)=1 P(S=∞)=1。记 p k = P ( A k ) p_k = \mathbb{P}(A_k) pk=P(Ak),则 S n S_n Sn 的方差为
V a r ( S n ) = E ( S n 2 ) − [ E ( S n ) ] 2 = E ( ∑ k = 1 n I k 2 + ∑ i ≠ j I i I j ) − ( ∑ k = 1 n p k ) 2 = ∑ k = 1 n E ( I k 2 ) + ∑ i ≠ j E ( I i ) E ( I j ) − ( ∑ k = 1 n p k ) 2 = ∑ k = 1 n p k + ∑ i ≠ j p i p j − ( ∑ k = 1 n p k ) 2 = ∑ k = 1 n p k + ( ∑ k = 1 n p k ) 2 − ∑ k = 1 n p k 2 − ( ∑ k = 1 n p k ) 2 = ∑ k = 1 n ( p k − p k 2 ) ≤ E ( S n ) \begin{aligned} Var(S_n) &= \mathbb{E}(S_n^2)-[\mathbb{E}(S_n)]^2 \\ &= \mathbb{E}\left(\sum_{k=1}^n \mathbb{I}_k^2 + \sum_{i\neq j} \mathbb{I}_i \mathbb{I}_j\right) - \left(\sum_{k=1}^n p_k\right)^2 \\ &= \sum_{k=1}^n \mathbb{E}(\mathbb{I}_k^2) + \sum_{i\neq j} \mathbb{E}(\mathbb{I}_i) \mathbb{E}(\mathbb{I}_j) - \left(\sum_{k=1}^n p_k\right)^2 \\ &= \sum_{k=1}^n p_k + \sum_{i\neq j} p_i p_j - \left(\sum_{k=1}^n p_k\right)^2 \\ &= \sum_{k=1}^n p_k + \left(\sum_{k=1}^n p_k\right)^2 - \sum_{k=1}^n p_k^2 - \left(\sum_{k=1}^n p_k\right)^2 \\ &= \sum_{k=1}^n (p_k - p_k^2) \\ &\leq \mathbb{E}(S_n) \end{aligned} Var(Sn)=E(Sn2)−[E(Sn)]2=E k=1∑nIk2+i=j∑IiIj −(k=1∑npk)2=k=1∑nE(Ik2)+i=j∑E(Ii)E(Ij)−(k=1∑npk)2=k=1∑npk+i=j∑pipj−(k=1∑npk)2=k=1∑npk+(k=1∑npk)2−k=1∑npk2−(k=1∑npk)2=k=1∑n(pk−pk2)≤E(Sn)
然后,
P ( S < E ( S n ) 2 ) ≤ P ( S n < E ( S n ) 2 ) = P ( S n − E ( S n ) < − E ( S n ) 2 ) ≤ P ( ∣ S n − E ( S n ) ∣ ≥ E ( S n ) 2 ) ≤ 4 V a r ( S n ) [ E ( S n ) ] 2 ( 由切比雪夫不等式 ) ≤ 4 E ( S n ) ( 因为 V a r ( S n ) ≤ E ( S n ) ) (4) \begin{aligned} \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right) &\leq \mathbb{P}\left(S_n < \frac{\mathbb{E}(S_n)}{2}\right) \\ &= \mathbb{P}\left(S_n - \mathbb{E}(S_n) < -\frac{\mathbb{E}(S_n)}{2}\right) \\ &\leq \mathbb{P}\left(\left|S_n - \mathbb{E}(S_n)\right| \geq \frac{\mathbb{E}(S_n)}{2}\right) \\ &\leq \frac{4 Var(S_n)}{[\mathbb{E}(S_n)]^2} \quad (\text{由切比雪夫不等式}) \\ &\leq \frac{4}{\mathbb{E}(S_n)} \quad (\text{因为 $Var(S_n)\leq \mathbb{E}(S_n)$}) \end{aligned} \tag{4} P(S<2E(Sn))≤P(Sn<2E(Sn))=P(Sn−E(Sn)<−2E(Sn))≤P(∣Sn−E(Sn)∣≥2E(Sn))≤[E(Sn)]24Var(Sn)(由切比雪夫不等式)≤E(Sn)4(因为 Var(Sn)≤E(Sn))(4)
注意 { S < E ( S n ) 2 } \{S < \frac{\mathbb{E}(S_n)}{2}\} {S<2E(Sn)} 上升到 { S < ∞ } \{S < \infty\} {S<∞},最后通过概率测度的连续性,
P ( S < ∞ ) = P ( ⋃ n = 1 ∞ { S < E ( S n ) 2 } ) = lim n → ∞ P ( S < E ( S n ) 2 ) ≤ lim n → ∞ 4 E ( S n ) = 0 , \mathbb{P}(S < \infty) = \mathbb{P}\left(\bigcup_{n=1}^\infty \{S < \frac{\mathbb{E}(S_n)}{2}\}\right) = \lim_{n \to \infty} \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right) \leq \lim_{n \to \infty} \frac{4}{\mathbb{E}(S_n)} = 0, P(S<∞)=P(n=1⋃∞{S<2E(Sn)})=n→∞limP(S<2E(Sn))≤n→∞limE(Sn)4=0,
那么我们得出
P ( S = ∞ ) = 1 − P ( S < ∞ ) = 1. \mathbb{P}(S = \infty) = 1 - \mathbb{P}(S < \infty) = 1. P(S=∞)=1−P(S<∞)=1.
■ \tag*{$\blacksquare$} ■
4. Erdös-Rényi 定理
上述定理中的成对独立条件可以进一步放宽,得到 Erdös-Rényi 定理。
定理(Erdös-Rényi)
假设 { A k } \{A_k\} {Ak} 是事件,如果
∑ k P ( A k ) = ∞ , \sum_k \mathbb{P}(A_k) = \infty, k∑P(Ak)=∞,
并且
lim inf n → ∞ ∑ j = 1 n ∑ k = 1 n P ( A j ∩ A k ) ( ∑ k = 1 n P ( A k ) ) 2 = 1 , (5) \liminf_{n \to \infty} \frac{\sum_{j=1}^n \sum_{k=1}^n \mathbb{P}(A_j \cap A_k)}{\left(\sum_{k=1}^n \mathbb{P}(A_k)\right)^2} = 1,\tag{5} n→∞liminf(∑k=1nP(Ak))2∑j=1n∑k=1nP(Aj∩Ak)=1,(5)
那么我们有
P ( A k i.o. ) = 1. \mathbb{P}(A_k\;\text{i.o.}) = 1. P(Aki.o.)=1.
证明
我们将使用与之前相同的记号 S n S_n Sn 和 S S S。因为
E ( S n 2 ) = E [ ( ∑ k = 1 n I k ) 2 ] = ∑ j , k = 1 n E ( I j I k ) = ∑ j , k = 1 n P ( A j ∩ A k ) , \mathbb{E}(S^2_n) = \mathbb{E}\left[\left(\sum_{k=1}^n \mathbb{I}_k\right)^2\right] = \sum_{j, k = 1}^n \mathbb{E}(\mathbb{I}_j \mathbb{I}_k) = \sum_{j, k = 1}^n \mathbb{P}(A_j \cap A_k), E(Sn2)=E (k=1∑nIk)2 =j,k=1∑nE(IjIk)=j,k=1∑nP(Aj∩Ak),
并且
E ( S n ) = ∑ k = 1 n P ( A k ) , \mathbb{E}(S_n) = \sum_{k=1}^n \mathbb{P}(A_k), E(Sn)=k=1∑nP(Ak),
因此 (5) 等价于
lim inf n → ∞ E ( S n 2 ) [ E ( S n ) ] 2 = 1 。 \liminf_{n \to \infty} \frac{\mathbb{E}(S^2_n)}{[\mathbb{E}(S_n)]^2} = 1。 n→∞liminf[E(Sn)]2E(Sn2)=1。
根据 (4) 的前四行,我们有
P ( S < E ( S n ) 2 ) ≤ 4 E ( S n 2 ) − [ E ( S n ) ] 2 [ E ( S n ) ] 2 = 4 ( E ( S n 2 ) [ E ( S n ) ] 2 − 1 ) , \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right) \leq 4\frac{\mathbb{E}(S_n^2) - [\mathbb{E}(S_n)]^2}{[\mathbb{E}(S_n)]^2} = 4\left(\frac{\mathbb{E}(S_n^2)}{[\mathbb{E}(S_n)]^2} - 1\right), P(S<2E(Sn))≤4[E(Sn)]2E(Sn2)−[E(Sn)]2=4([E(Sn)]2E(Sn2)−1),
然后我们有
P ( S < ∞ ) = P ( ⋃ n = 1 ∞ { S < E ( S n ) 2 } ) = lim n → ∞ P ( S < E ( S n ) 2 ) ( 因为 { S < E ( S n ) 2 } 递增,且根据单调收敛定理 ) = lim inf n → ∞ P ( S < E ( S n ) 2 ) ( 因为最后极限由单调收敛定理存在 ) ≤ 4 ( lim inf n → ∞ E ( S n 2 ) [ E ( S n ) ] 2 − 1 ) = 0 , \begin{aligned} \mathbb{P}(S < \infty) &= \mathbb{P}\left(\bigcup_{n=1}^\infty \{S < \frac{\mathbb{E}(S_n)}{2}\}\right) \\ &= \lim_{n \to \infty} \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right)\quad (\text{因为 $\{S < \frac{\mathbb{E}(S_n)}{2}\}$ 递增,且根据单调收敛定理}) \\ &= \liminf_{n \to \infty} \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right)\quad (\text{因为最后极限由单调收敛定理存在}) \\ &\leq 4\left(\liminf_{n \to \infty} \frac{\mathbb{E}(S^2_n)}{[\mathbb{E}(S_n)]^2} - 1\right) = 0, \end{aligned} P(S<∞)=P(n=1⋃∞{S<2E(Sn)})=n→∞limP(S<2E(Sn))(因为 {S<2E(Sn)} 递增,且根据单调收敛定理)=n→∞liminfP(S<2E(Sn))(因为最后极限由单调收敛定理存在)≤4(n→∞liminf[E(Sn)]2E(Sn2)−1)=0,
这表明
P ( S = ∞ ) = 1 − P ( S < ∞ ) = 1. \mathbb{P}(S = \infty) = 1 - \mathbb{P}(S < \infty) = 1. P(S=∞)=1−P(S<∞)=1.
■ \tag*{$\blacksquare$} ■
参考文献
- Kai Lai Chung, A Course in Probability Theory, 第三版 (2001)
- Rick Durrett, Probability: Theory and Examples, 第五版 (2019)
相关文章:

Borel-Cantelli 引理
翻译自大佬 https://huarui1998.com/Notes/math/borel-cantelli.html 1. 集序列的 lim inf \lim\inf liminf 和 lim sup \lim\sup limsup 类似于定义实数序列 { a k } \{a_k\} {ak} 的 lim inf \lim\inf liminf 和 lim sup \lim\sup limsup, …...

算法训练营第四十一天 | LeetCode 509 斐波那契数列、LeetCode 70 爬楼梯、LeetCode 746 使用最小花费爬楼梯
LeetCode 509 斐波那契数列 这题动规五部曲都定义得比较明确。首先是dp数组下标,题目中给定F(0) 0说明从0开始,dp[i]直接表示F(i)的值即可。递推公式也直接给出了,也给了开头两个作为递推基础的数值作为初始化依据。遍历顺序也指明是从前往…...
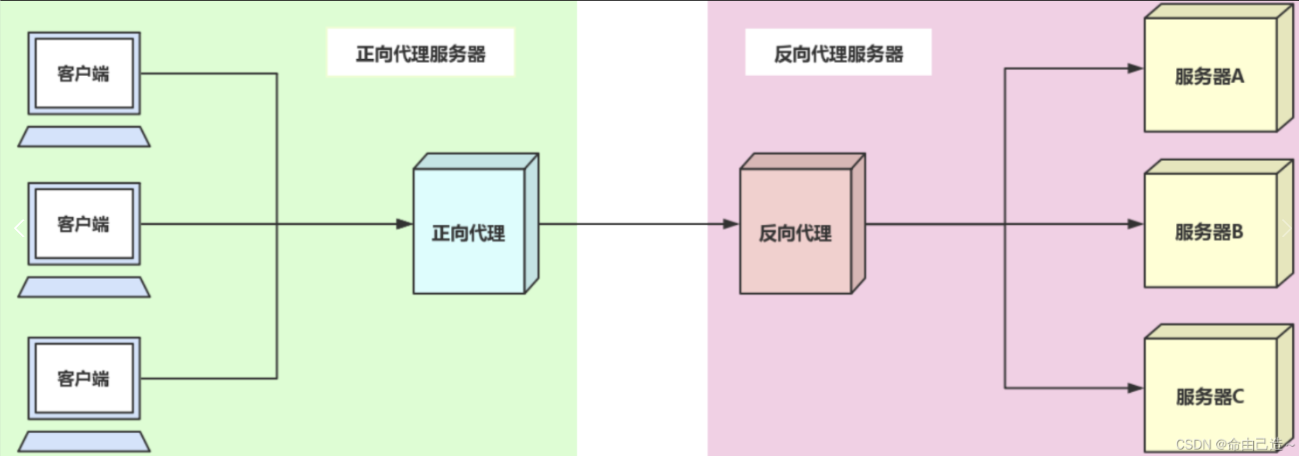
网络其他重要协议(DNS、ICMP、NAT)
1.DNS DNS是一整套从域名映射到IP的系统 1.1 DNS背景 TCP/IP中使用IP地址和端口号来确定网络上的一台主机的一个程序,但是IP地址不方便记忆,例如我们想访问百度就会在浏览器中输入baidu.com而不是百度的IP地址。于是人们发明了一种叫主机名的东西, 是…...
进行组合约束建模)
利用PyCSP3库(含大量全局约束)进行组合约束建模
文章目录 1. 什么是 PyCSP3 ?2. 安装方法(Windows)2.1 通过 Google_colab 直接运行2.2 通过 pip 进行安装3. 快速入门3.1 声明变量3.2 更新约束3.3 定义目标3.4 常用的全局约束1. 什么是 PyCSP3 ? PyCSP3 是 Python 中的一个库,用于对组合约束问题进行建模,包括 约束满足…...

解决updateByExample时属性值异常的问题(部分属性值没有使用占位符?进行占位,而是变成了属性的名称)
目录 场景简介代码片断实体类 报错信息排查原因解决测试过程解决方案 场景简介 1、程序将mybatis框架升级为3.5.9版本后执行updateByExample方法时报错 代码片断 Condition condition new Condition(MbCcsSessionConfig.class); condition.createCriteria().andEqualTo(&quo…...

[C++][algorithm][Eigen] 基于Eigen实现Softmax函数
1 简介 Softmax函数是机器学习和深度学习中一个非常重要的激活函数,它在多分类问题中尤其关键。Softmax函数能够将一个向量或一组实数转换成概率分布,使得每个元素的值都在0到1之间,并且所有元素的和为1。本博客文章《【Eigen】基于Eigen实现…...
一招教大家,如何移除受保护的excel工作表的编辑权限限制?
有时候,我们打开工作表发现只有部分单元格可以编辑,点击其他单元格都显示“您试图更改的单元格或图标受保护”,既没法正常编辑或下拉填充,也没有办法快捷筛选。这时候我们可以通过输入密码解除保护,就可以正常编辑了。…...
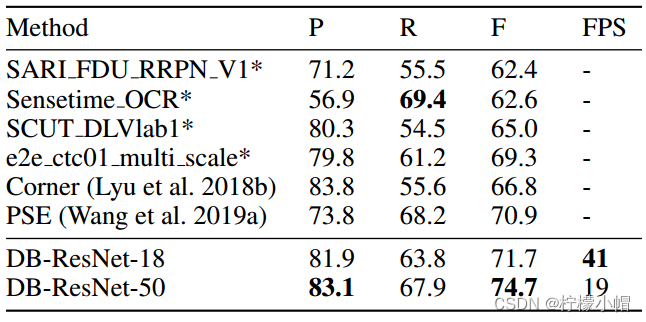
Python 全栈体系【四阶】(五十三)
第五章 深度学习 十二、光学字符识别(OCR) 2. 文字检测技术 2.3 DB(2020) DB全称是Differentiable Binarization(可微分二值化),是近年提出的利用图像分割方法进行文字检测的模型。前文所提…...

民国漫画杂志《时代漫画》第27期.PDF
时代漫画27.PDF: https://url03.ctfile.com/f/1779803-1248635258-b6a842?p9586 (访问密码: 9586) 《时代漫画》的杂志在1934年诞生了,截止1937年6月战争来临被迫停刊共发行了39期。 ps: 资源来源网络!...
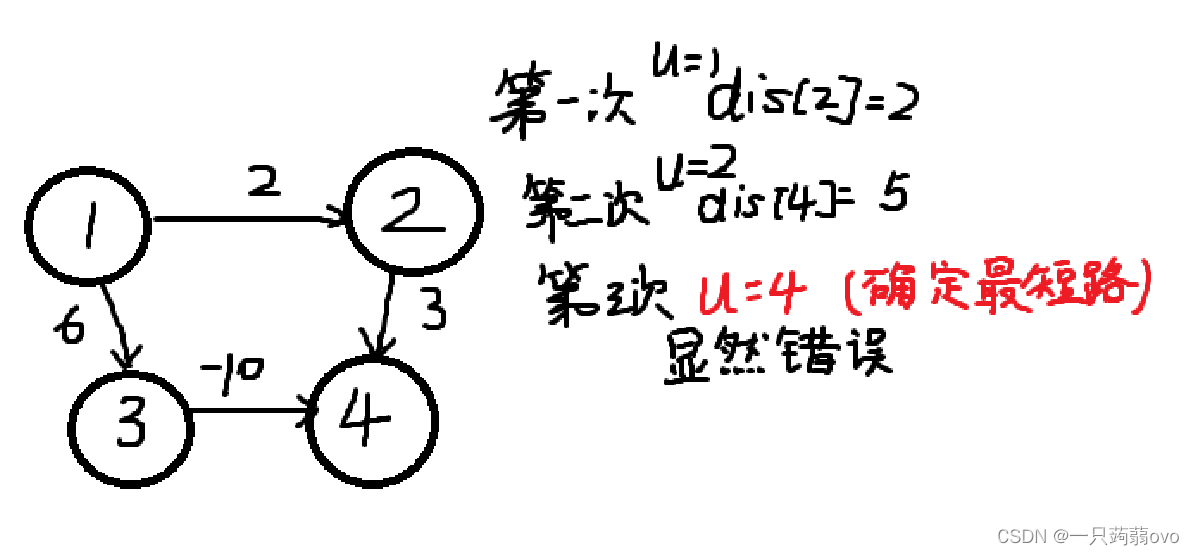
图论(四)—最短路问题(Dijkstra)
一、最短路 概念:从某个点 A 到另一个点B的最短距离(或路径)。从点 A 到 B 可能有多条路线,多种距离,求其中最短的距离和相应路径。 最短路径分类: 单源最短路:图中的一个点到其余各点的最短路径…...
用友NC linkVoucher SQL注入漏洞复现
0x01 产品简介 用友NC是由用友公司开发的一套面向大型企业和集团型企业的管理软件产品系列。这一系列产品基于全球最新的互联网技术、云计算技术和移动应用技术,旨在帮助企业创新管理模式、引领商业变革。 0x02 漏洞概述 用友NC /portal/pt/yercommon/linkVoucher 接口存在…...

部署Prometheus + Grafana实现监控数据指标
1.1 Prometheus安装部署 Prometheus监控服务 主机名IP地址系统配置作用Prometheus192.168.110.27/24CentOS 7.94颗CPU 8G内存 100G硬盘Prometheus服务器grafana192.168.110.28/24CentOS 7.94颗CPU 8G内存 100G硬盘grafana服务器 监控机器 主机名IP地址系统配置k8s-master-0…...
GEE27:遥感数据可用数据源计算及条带号制作
1.写在前面 🌍✨今天读了一篇关于遥感数据可用数据源计算及条带号制作的文章,结合着自己的理解,添加了一些内容。 2.GEE代码 📚📚这段代码的主要作用是利用Google Earth Engine平台,通过分析Landsat 8影…...

FURNet问题
1. 为什么选择使用弱监督学习? 弱监督学习减少了对精确标注数据的依赖,这在医学图像处理中尤为重要,因为高质量标注数据通常需要大量专业知识和时间。弱监督学习通过利用少量标注数据或粗略标注数据来训练模型,降低了数据准备的成…...
抖音小店怎么对接达人合作?达人带货的细节分享,附邀约达人话术
大家好,我是电商花花 人有多大胆,地就有多大产,做抖店想要出单,爆单,那必须要对接大量的达人来帮我们带货,抖音小店就是直播电商,帮我们对接的达人越多,出单就越多。 所以做抖店如…...
迈向未来:Web3 技术开发的无限可能
在当今的数字时代,互联网技术日新月异,推动着各行各业的变革与发展。从Web1.0的信息发布,到Web2.0的社交互动,互联网的每一次进化都为人们的生活带来了深远的影响。如今,Web3的到来正在开启一个全新的时代,…...
)
Python应用开发——30天学习Streamlit Python包进行APP的构建(2)
🗓️ 天 14 Streamlit 组件s Streamlit 组件s 是第三方的 Python 模块,对 Streamlit 进行拓展 [1]. 有哪些可用的 Streamlit 组件s? 好几十个精选 Streamlit 组件s 罗列在 Streamlit 的网站上 [2]. Fanilo(一位 Streamlit 创作者)在 wiki 帖子中组织了一个很棒的 St…...

Leecode热题100---46:全排列(递归)
题目: 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 思路: 元素交换函数递归: 通过交换元素来实现全排列。即对于[x, nums.size()]中的元素,for循环遍历每个元素分别成…...

Android 多语言
0. Locale方法 Locale locale Locale.forLanguageTag("zh-Hans-CN"); 执行如下方法返回字符串如下: 方法 英文下执行 中文下执行 备注 getLanguage()zhzhgetCountry()CNCNgetDisplayLanguage()zh中文getDisplayCountry()CN中国getDisplayName()zh (…...

Thingsboard规则链:Message Type Filter节点详解
一、Message Type Filter节点概述 二、具体作用 三、使用教程 四、源码浅析 五、应用场景与案例 智能家居自动化 工业设备监控 智慧城市基础设施管理 六、结语 在物联网(IoT)领域,数据处理与自动化流程的实现是构建智能系统的关键。作…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
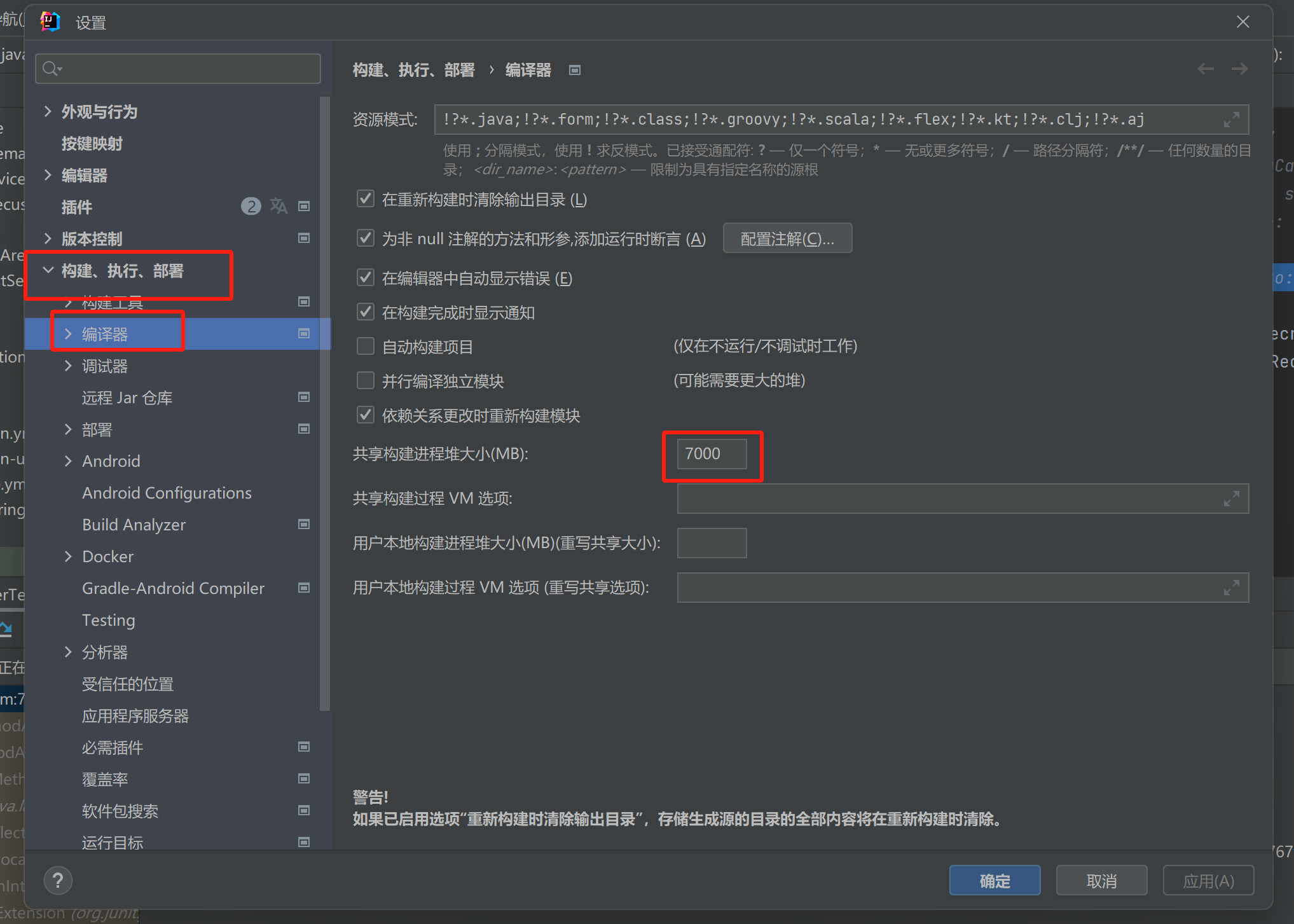
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
