当前位置： 首页 > news >正文

不含一阶导数项的线性二阶微分方程的通解

news 2026/2/9 2:17:08

假设这里有一个线性二阶微分等式，形式如下：

y^{''}+F(\theta)y=f(\theta)           （1）

其中F是连续的，f是在实闭区间是\theta_{0}\leq \theta \leq \theta_{f}连续的,如果有人倾向于推广，在相对假弱的假设下，这个结果能够被发现。如果\varphi_{1},\varphi_{2}是下列其次线性方程的任意两个线性无关的解

y^{''}+F(\theta)y=0                 （2）

于是，关于\varphi_{1},\varphi_{2}的朗斯基行列式被定义为\varphi_{1}\varphi_{2}^{'}-\varphi_{2}\varphi_{1}^{'}，很显然是一个常值\theta_{0}\leq \theta \leq \theta_{f}，因为

(\varphi_{1}\varphi_{2}^{'}-\varphi_{2}\varphi_{1}^{'})^{'}=\varphi_{1}\varphi_{2}^{''}-\varphi_{2}\varphi_{1}^{''}=-F\varphi_{1}\varphi_{2}+F\varphi_{1}\varphi_{2}=0                     （3）

因为\varphi_{1},\varphi_{2}能够被任意非零的常数乘，它是可能的来归一化这些常值使其满足

\varphi_{1}\varphi_{2}^{'}-\varphi_{2}\varphi_{1}^{'}=1,\theta_{0}\leq\theta\leq\theta_{f}                     （4）

因此，\varphi_{1},\varphi_{2}代表线性方程（2）的线性独立解，并且满足（4）式。

引入一个新的函数，让我们联想到朗斯基行列式，但是与f有关，按如下形式定义：

w(f)=S(\varphi_{1}f)\varphi_{2}-S(\varphi_{2}f)\varphi_{1}           （5）

其中S(\varphi_{1}f)=\int_{\theta_{0}}^{\theta}\varphi_{1}(\tau)f(\tau)\textup{d}\tau,S(\varphi_{2}f)=\int_{\theta_{0}}^{\theta}\varphi_{2}(\tau)f(\tau)\textup{d}\tau

观察得到

\frac{\textup{d}^{2}w(f)}{\textup{d}\theta^{2}}=S(\varphi_{1}f)\varphi_{2}^{''}-S(\varphi_{2}f)\varphi_{1}^{''}+f         （6）

代入（1）式，可以得到w是该线性二阶微分方程的特解，于是，整个问题的解可以写为

y^{*}=c_{1}\varphi_{1}+c_{2}\varphi_{2}+w(f)              （7）

其中c_{1},c_{2}可以是任意的常数

相关文章：

不含一阶导数项的线性二阶微分方程的通解

假设这里有一个线性二阶微分等式，形式如下： （1） 其中是连续的，是在实闭区间是连续的,如果有人倾向于推广，在相对假弱的假设下，这个结果能够被发现。如果是下列其次线性方程的任意两个线性无关的…...

编程日记 2024/5/27 22:27:32

Redis篇 String

String概念和set,get扩充 一. String类型的基本介绍二. String中set,get方法扩充 一. String类型的基本介绍 redis中所有的key都是字符串类型的,但是value的类型差异很大. redis中的字符串,直接就是二进制方式存储的,可以存储整数,二进制数据 文本数据,Json,xml还有音频等. 二.…...

编程日记 2024/5/27 22:25:31

【vue-2】v-on、v-show、v-if及按键修饰符

目录 1、v-on事件 2、按键修饰符 3、显示和隐藏v-show 4、条件渲染v-if 1、v-on事件 创建button按钮有以下两种方式&#xff1a; <button v-on:click"edit">修改</button> <button click"edit">修改</button> 完整示例代码…...

编程日记 2024/5/27 22:24:30

华为交换机基础实验----VLAN基础

交换机篇实验&#xff1a; 给交换机创建VLAN 1.单个VLAN的创建 [S]vlan 10 查看的方法&#xff1a;dis vlan 2.批量创建vlan的方法 Vlan b 20 30 40 连续创建三个vlan&#xff0c;分别为vlan20 vlan30和vlan40 [SONY-S1-vlan10]vlan b 20 30 40 3.批量创建连续的vlan&#xf…...

编程日记 2024/5/27 22:23:29

Vue3学习使用axios和qs进行POST请求和响应处理

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 一、前言1.准备工作2.发送POST请求3.处理响应数据4.总结 一、前言 在前端开发中&#xff0c;经常需要与后端进行数据交互&#xff0c;其中包括发送POST请求并处理响…...

编程日记 2024/5/27 22:22:28

张大哥笔记：赚钱高手养成计划---如何将一份时间产生N份收入？

我们常说的赚钱的四种境界有哪些&#xff1f; 1.靠体力挣钱 2.靠技能挣钱 3.靠知识挣钱 4.靠平台钱生钱 所以对应的收入的模式就会是下面4种模式&#xff1a; 1.一份时间卖1次 2.一份时间卖N次 3.一份时间溢价卖N次 4.购买他人时间为自己所用 时间对于每个人都是相同的…...

编程日记 2024/5/27 22:21:26

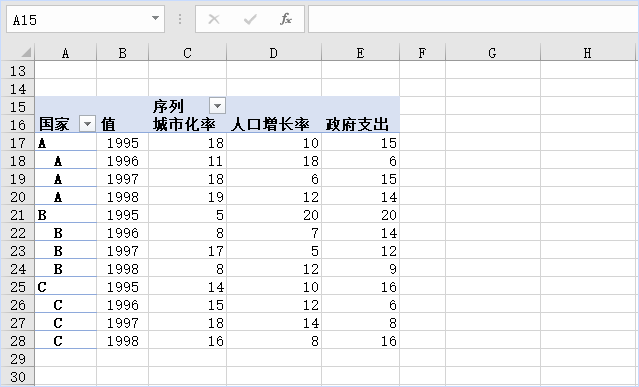
excel里如何将数据分组转置？

这个表格怎样转换为下表&#xff1f;按照国家来分组&#xff0c;把不同年份对应的不同序列值进行转置&#xff1f;&#xff1f; 这演示用数据透视表就完成这个数据转换。 1.创建数据透视表 选中数据中任意单元格&#xff0c;点击插入选项卡&#xff0c;数据透视表&#xff0c;…...

编程日记 2024/5/27 22:20:25

WHAT - 前端安全性测试和常见攻击手段

目录 一、安全性测试二、前端安全性测试三、跨站脚本&#xff08;XSS&#xff09;攻击1. 介绍2. 三大类型反射型 XSS&#xff08;Reflected XSS&#xff09;存储型 XSS&#xff08;Stored XSS&#xff09;DOM 型 XSS&#xff08;DOM-based XSS&#xff09; 3. xss 盲打4. xss 水…...

编程日记 2024/5/27 22:19:24

重量and体积，不要在傻傻的花冤枉钱寄快递了！

寄快递时有没有遇到过明明不重却被按体积收费的情况&#xff1f;别急&#xff0c;今天就来给大家揭秘快递收费的奥秘&#xff01; 实际重量和体积重量&#xff01; 首先&#xff0c;我们要明白两个概念&#xff1a;实际重量和体积重量。实际重量就是你看到的物品重量&#xf…...

编程日记 2024/5/27 22:18:23

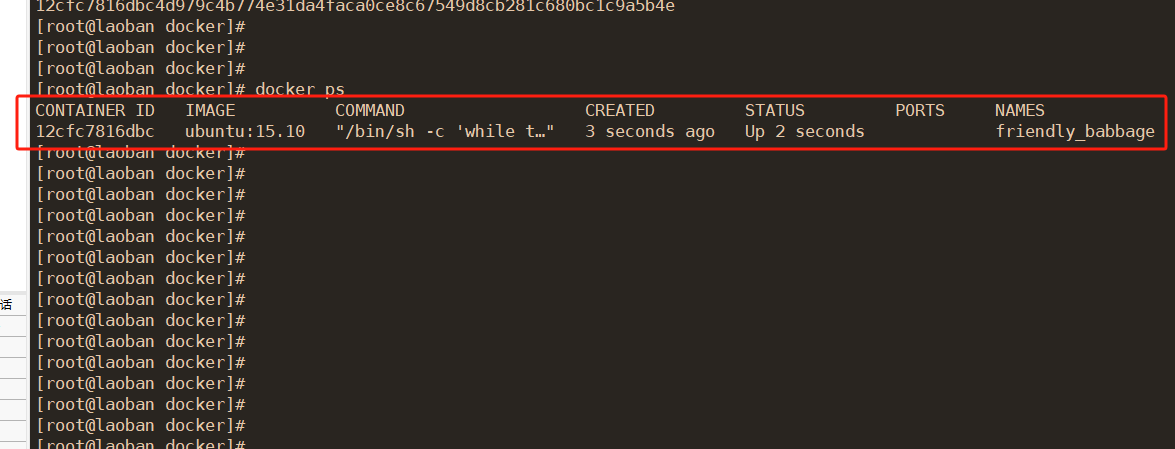
docker ps显示的参数具体是什么意思

1&#xff0c;运行一个容器 docker run -d ubuntu:15.10 /bin/sh -c "while true; do echo hello world; sleep 1; done"这段命令的作用是使用 docker run 命令运行一个基于 ubuntu:15.10 镜像的 Docker 容器&#xff0c;并在容器中执行一个无限循环的命令。 具体解…...

编程日记 2024/5/27 22:17:22

【C++】多态：编程中的“一人千面”艺术

目录 一、多态的概念二、多态的定义及实现1.多态的构成条件2.虚函数的重写2.1 什么是虚函数&#xff1f;2.2 虚函数的重写是什么&#xff1f;2.3 虚函数重写的两个例外2.4 C11 override 和 final2.5 重载、覆盖(重写)、隐藏(重定义)的对比 三、抽象类3.1 概念3.2 接口继承和实现…...

编程日记 2024/5/27 22:16:21

【必备工具】gitee上传-保姆级教程

目录 1.gitee是什么 2.gitee怎么注册 ​编辑 3.gitee怎么提交代码 4.gitee的三板斧 Clone仓库 Q&A 1. Gitee 只有三板斧吗&#xff1f; 2. Git 教了&#xff0c;Gitee 上没有绿点怎么办&#xff1f; 3. 用户名和密码输入错误怎么办&#xff1f; 4. 操作时不小心…...

编程日记 2024/5/27 22:15:20

P1115 最长子段和

题目描述 给出一个长度为 &#x1d45b;n 的序列 &#x1d44e;a&#xff0c;选出其中连续且非空的一段使得这段和最大。 输入格式 第一行是一个整数&#xff0c;表示序列的长度 &#x1d45b;。 第二行有 &#x1d45b;n 个整数&#xff0c;第 &#x1d456; 个整数表示序列的…...

编程日记 2024/5/27 22:14:19

02 FreeRTOS 任务

1、创建任务函数 1.1 动态内存的使用 在之前我们如果要创建一个与学生有关的任务&#xff0c;我们会定义&#xff1a; //打印50个学生的信息 char name[50][100]; int age[50]; int sex[50]; //1表示男&#xff0c;0表示女 int score[50]; 如果之后要对其进行修改会非常麻烦&…...

编程日记 2024/5/27 22:13:17

NSS题目练习4

[LitCTF 2023]1zjs 打开后是一个游戏&#xff0c;用dirsearch扫描&#xff0c;什么都没发现 查看源代码搜索flag&#xff0c;发现没有什么用 搜索php&#xff0c;访问 出现一堆符号&#xff0c;看样子像是jother编码 解码得到flag&#xff0c;要删掉[] [LitCTF 2023]Http pro …...

编程日记 2024/5/27 22:11:15

【算法】合并k个已排序的链表

✨题目链接&#xff1a; NC51 合并k个已排序的链表 ✨题目描述 合并 k 个升序的链表并将结果作为一个升序的链表返回其头节点。 数据范围&#xff1a;节点总数 0≤&#x1d45b;≤50000≤n≤5000&#xff0c;每个节点的val满足 ∣&#x1d463;&#x1d44e;&#x1d459;∣&…...

编程日记 2024/5/27 22:10:14

【Muduo】三大核心之EventLoop

Muduo网络库的EventLoop模块是网络编程框架中的核心组件&#xff0c;负责事件循环的驱动和管理。以下是对EventLoop模块的详细介绍&#xff1a; 作用与功能&#xff1a; EventLoop是网络服务器中负责循环的重要模块&#xff0c;它持续地监听、获取和处理各种事件&#xff0c;…...

编程日记 2024/5/27 22:07:09

ubuntu安装完桌面后如何启动

ubuntu安装完桌面后如何启动 在Ubuntu服务器上安装桌面环境后&#xff0c;您可以使用以下命令启动图形界面&#xff1a; sudo systemctl start gdm3如果您使用的是Ubuntu 20.04或更新版本&#xff0c;可能需要使用gdm3作为显示管理器。在早期的Ubuntu版本中&#xff0c;可能使…...

编程日记 2024/5/27 22:05:07

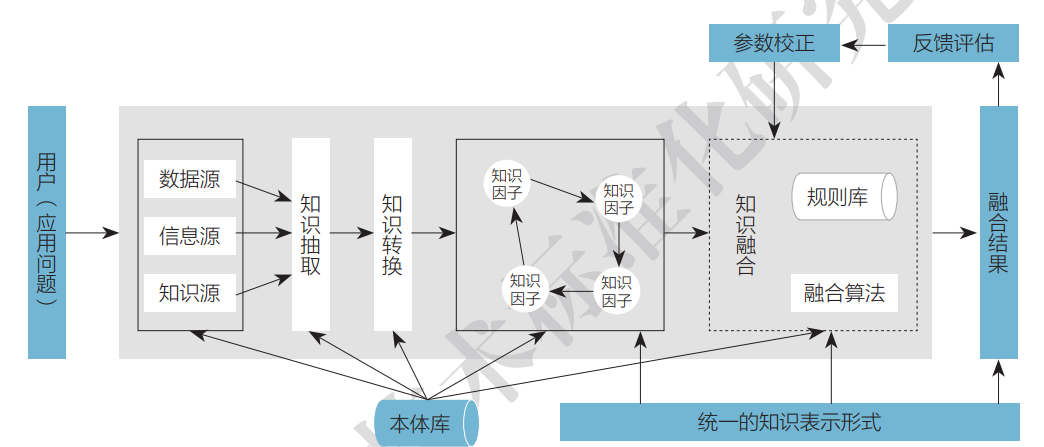
知识融合概述

文章目录 知识融合知识融合过程研究现状技术发展趋势 知识融合 知识融合的概念最早出现在1983年发表的文献中&#xff0c;并在20世纪九十年代得到研究者的广泛关注。而另一种知识融合的定义是指对来自多源的不同概念、上下文和不同表达等信息进行融合的过程认为知识融合的目标是…...

编程日记 2024/5/27 22:03:04

LIO-EKF: High Frequency LiDAR-Inertial Odometry using Extended Kalman Filters

一、论文摘要 里程计估计是每个需要在未知环境中导航的自主系统的关键要素。在现代移动机器人中&#xff0c;3D LiDAR 惯性系统通常用于执行此任务。通过融合 LiDAR 扫描和 IMU 测量&#xff0c;这些系统可以减少因顺序注册各个 LiDAR 扫描而引起的累积漂移&#xff0c;并提供稳…...

编程日记 2024/5/27 22:02:03

mongodb源码分析session执行handleRequest命令find过程

mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程&#xff0c;并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令&#xff0c;把数据流转换成Message&#xff0c;状态转变流程是&#xff1a;State::Created 》 St…...

编程新知 2026/1/15 4:39:38

vue3 字体颜色设置的多种方式

在Vue 3中设置字体颜色可以通过多种方式实现&#xff0c;这取决于你是想在组件内部直接设置&#xff0c;还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法&#xff1a; 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

编程新知 2026/2/4 20:47:44

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候&#xff0c;写过一篇简单实现&#xff0c;后期随着对该模型的深入研究&#xff0c;本次记录涉及到prophet 的公式以及参数调优&#xff0c;从公式可以更直观…...

编程新知 2026/1/27 5:01:54

Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！

一、引言 在数据驱动的背景下&#xff0c;知识图谱凭借其高效的信息组织能力&#xff0c;正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合&#xff0c;探讨知识图谱开发的实现细节&#xff0c;帮助读者掌握该技术栈在实际项目中的落地方法。 …...

编程新知 2025/9/17 21:39:04

2023赣州旅游投资集团

单选题 1.“不登高山&#xff0c;不知天之高也&#xff1b;不临深溪&#xff0c;不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

编程新知 2025/11/8 16:42:13

力扣-35.搜索插入位置

题目描述 给定一个排序数组和一个目标值&#xff0c;在数组中找到目标值&#xff0c;并返回其索引。如果目标值不存在于数组中&#xff0c;返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

编程新知 2025/12/3 3:22:43

HashMap中的put方法执行流程（流程图）

1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中&#xff0c;其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下&#xff1a; 初始判断与哈希计算&#xff1a; 首先&#xff0c;putVal 方法会检查当前的 table&#xff08;也就…...

编程新知 2026/2/8 3:32:52

人机融合智能 | “人智交互”跨学科新领域

本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

编程新知 2026/1/25 13:33:35

处理vxe-table 表尾数据是单独一个接口，表格tableData数据更新后，需要点击两下，表尾才是正确的

修改bug思路&#xff1a; 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑&#xff1a;async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

编程新知 2026/1/25 6:16:49

TMC2226超静音步进电机驱动控制模块

目前已经使用TMC2226量产超过20K，发现在静音方面做的还是很不错。 一、TMC2226管脚定义说明 二、原理图及下载地址 一、TMC2226管脚定义说明 引脚编号类型功能OB11电机线圈 B 输出 1BRB2线圈 B 的检测电阻连接端。将检测电阻靠近该引脚连接到地。使用内部检测电阻时，将此引…...

编程新知 2025/7/6 6:43:40