【论文笔记】advPattern
【论文题目】
advPattern: Physical-World Attacks on Deep Person Re-Identification via Adversarially Transformable Patterns
Abstract
本文首次尝试对深度reID实施鲁棒的物理世界攻击。提出了一种新颖的攻击算法,称为advPattern,用于在衣服上生成对抗模式,它通过学习不同相机之间图像对的变化来拉近来自同一相机的图像特征,同时将来自不同相机的特征推得更远。通过穿着本文设计的"隐形斗篷",敌手可以逃避人员搜索,或者假冒目标人员来欺骗物理世界中的深度身份识别模型。
使用Market1501和本文建立的PRCS数据集评估本文的可变换模式在对手服装上的有效性。实验结果表明,在逃避攻击下,reID模型匹配对手的rank-1准确率从87.9%下降到27.1%。此外,在模拟攻击下,敌手可以以47.1%的1级准确率和67.9 %的mAP模拟目标人物。结果表明,深度reID系统容易受到我们的物理攻击。
3 System Model
在这一部分中,我们首先介绍了威胁模型,然后介绍了我们的设计目标。
3.1 Threat Model
工作主要集中在对基于DNN的reID系统的物理可实现的攻击上,该系统可以实时捕获行人,并在非重叠的摄像机中自动搜索感兴趣的人。
通过将探测图像(probe image, 查询的图像)提取的特征与从其他相机实时采集的一组不断更新的画廊图像(gallery image)的特征进行比较,reID系统从图库中输出被认为与查询图像最相似的图像。
假设攻击者对训练好的深度reID模型具有白盒访问权限,因此他具有模型结构和参数的知识,并且只在推理阶段对reID模型实施攻击。不允许对手操纵数字查询图像或从相机收集的图库图像。 此外,对手在攻击reID系统时不得改变自己的物理外观,以免引起人类监督者的怀疑。这些合理的假设使得在reID系统上成功实现物质世界攻击具有一定的挑战性。
3.2 Design Objectives
提出两种攻击情境,逃避攻击(Evading Attack)和冒充攻击(Impersonation Attack)。
逃避攻击:躲避攻击是一种无针对性的攻击:reID模型被愚弄,将对手比作一个除自己之外的任何人,看起来好像对手穿着隐形斗篷。形式上,一个reID模型 f θ ( ⋅ , ⋅ ) f_\theta(\cdot,\cdot) fθ(⋅,⋅)输出一对图像的相似度分数,其中 θ \theta θ是模型参数。给定对手的探测图像 p a d v p_{adv} padv,对手的画廊图像 g a d v g_{adv} gadv,尝试找到一个贴到对手衣服上的图案 δ \delta δ,通过下面的优化问题,使得reID模型错误识别:
max D ( δ ) , s . t . R a n k ( f θ ( p a d v + δ , g a d v + δ ) ) > K (1) \max D(\delta), s.t. Rank(f_\theta(p_{adv+\delta},g_{adv+\delta}))>K\tag{1} maxD(δ),s.t.Rank(fθ(padv+δ,gadv+δ))>K(1)
其中 D ( ⋅ ) D(\cdot) D(⋅)用于测量生成的图案的真实性。与以往的工作旨在生成视觉上不明显的扰动不同,本文尝试为摄像头传感生成可见图案,同时使生成的图案与衣服上的自然装饰图案无法区分。只有当图像对 ( p a d v + δ , g a d v + δ ) (p_{adv+\delta},g_{adv+\delta}) (padv+δ,gadv+δ)排在top-K结果后面时,对抗模式才能成功构建,这意味着reID系统无法实现对手的跨相机图像匹配。
冒充攻击:是一种目标攻击(targetted attack),可以看作是逃避攻击的一种扩展:对手试图欺骗身份识别模型,使其将自己识别成目标身份。
给定目标身份图像 I t I_t It,形式上冒充攻击是优化下面的优化过程:
max D ( δ ) , s . t . { R a n k ( f θ ( p a d v + δ , g a d v + δ ) ) > K R a n k ( f θ ( p a d v + δ , I t ) ) < K (2) \max D(\delta), s.t. \begin{equation} \left\{ \begin{aligned} Rank(f_\theta(p_{adv+\delta},g_{adv+\delta}))>K \\ Rank(f_\theta(p_{adv+\delta}, I_t)) < K \end{aligned} \right. \end{equation}\tag{2} maxD(δ),s.t.{Rank(fθ(padv+δ,gadv+δ))>KRank(fθ(padv+δ,It))<K(2)
4 Adversarial Pattern Generation
4.1 Transformable Patterns across Camera Views
对于逃避攻击,给定由对手构建的生成集 X = ( x 1 , x 2 , ⋯ , x m ) X=(x_1,x_2,\cdots,x_m) X=(x1,x2,⋯,xm),包含了从 m m m个不同的摄像机捕捉的对手图片。对于每张 X X X中图像 x i x_i xi,计算对抗图像 x i ′ = o ( x i , T i ( δ ) ) x_i'=o(x_i,T_i(\delta)) xi′=o(xi,Ti(δ))。这表示将变换后的 x i x_i xi对应区域 T i ( ⋅ ) T_i(\cdot) Ti(⋅)与生成的图案 δ δ δ进行叠加。这里 T i ( δ ) T_i(\delta) Ti(δ)是对 δ \delta δ的透视变换操作。
通过优化下面的问题生成可转移的对抗性图案 δ \delta δ:
argmin δ ∑ i = 1 m ∑ j = 1 m f θ ( x i ′ , x j ′ ) , s . t . i ≠ j (3) {\underset{\delta}{\operatorname{arg min}}}\sum_{i=1}^m\sum_{j=1}^m f_\theta(x_i',x_j'),s.t. i\neq j\tag{3} δargmini=1∑mj=1∑mfθ(xi′,xj′),s.t.i=j(3)
迭代地最小化来自不同摄像机的对手图像的相似度分数,以通过生成的对抗模式逐渐进一步提取来自不同摄像机的对手图像的特征。
对于冒充攻击,给定目标行人图像 I t I_t It,优化下面问题:
argmin δ ∑ i = 1 m ∑ j = 1 m f θ ( x i ′ , x j ′ ) − α ( f θ ( x i ′ , I t ) + f θ ( x j ′ , I t ) ) , s . t . i ≠ j (4) {\underset{\delta}{\operatorname{arg min}}}\sum_{i=1}^m\sum_{j=1}^m f_\theta(x_i',x_j')-\alpha(f_\theta(x_i',I_t)+f_\theta(x_j',I_t)),s.t. i\neq j\tag{4} δargmini=1∑mj=1∑mfθ(xi′,xj′)−α(fθ(xi′,It)+fθ(xj′,It)),s.t.i=j(4)
其中 α \alpha α控制不同项的强度。通过在Eq.4中加入第二项,额外最大化敌手图像与目标人物图像的相似性分数,以生成一个更强大的对抗模式来拉近敌手图像与目标人物图像的提取特征。
4.2 Scalable Patterns in Varying Positions
对抗模式应该能够在任何位置实施成功的攻击,这意味着攻击应该与位置无关。为了实现这一目标,本文进一步改进了对抗模式在不同位置上的可扩展性。
由于无法精确捕捉视角变换的分布,因此采用多位置采样策略增加生成集的体量,以近似生成可扩展对抗性图案的图像分布。对抗者的扩展生成集 X C X^C XC是通过收集从各个摄像机视角拍摄的不同距离和角度的对抗者图像,并对原始收集的图像进行平移和缩放等图像变换合成实例构建的。
对于逃避攻击,从 X C X^C XC中给定三元组 t r i k = < x k o , x k + , x k − > tri_k=<x_k^o,x_k^+,x_k^-> trik=<xko,xk+,xk−>,其中 x k o x_k^o xko和 x k + x_k^+ xk+是同一摄像机下的行人图像,和 x k − x_k^- xk−是不同摄像机下的行人图像。对于 t r i k tri_k trik中的每个图像 x k x_k xk,计算对抗图像 x k ′ x_k' xk′为 o ( x k , T k ( δ ) ) o(x_k,T_k(\delta)) o(xk,Tk(δ))。每次迭代时随机选择一个三元组来求解下列优化问题:
argmin δ E t r i k ∼ X C f θ ( ( x k o ) ′ , ( x k − ) ′ ) − β f θ ( ( x k o ) ′ , ( x k + ) ′ ) (5) {\underset{\delta}{\operatorname{arg min}}} \mathbb{E}_{tri_k\sim X^C} f_\theta((x_k^o)',(x_k^-)')-\beta f_\theta((x_k^o)',(x_k^+)')\tag{5} δargminEtrik∼XCfθ((xko)′,(xk−)′)−βfθ((xko)′,(xk+)′)(5)
其中 β \beta β是权衡不同项的超参数。式中:目标式Eq.5是最小化 x k o x_k^o xko与 x k − x_k^- xk−的相似度得分,以区分跨摄像机视角的行人图像,而最大化 x k o x_k^o xko与 x k + x_k^+ xk+的相似度得分,以保持同一摄像机视角下行人图像的相似性。
在优化过程中,生成模式从增广生成集 X C X^C XC中学习可伸缩性,以拉近从同一相机中提取的人物图像特征,同时将来自不同相机的特征推得更远,如图4所示。
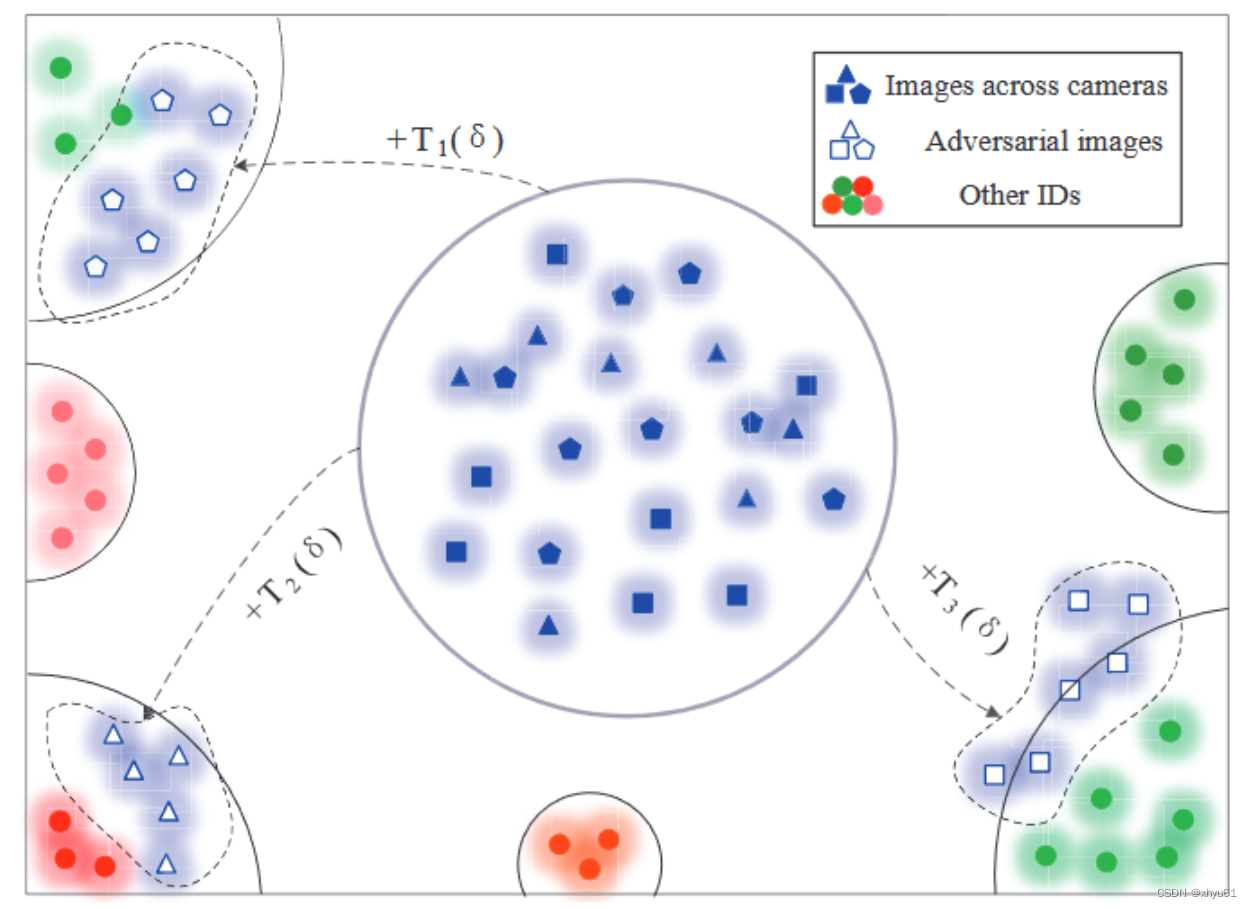
图4:可扩展对抗模式如何工作的说明。通过添加生成的对抗模式,将来自同一相机视图的对抗图像在特征空间中聚集在一起。同时,来自不同摄像头的对抗图像的距离变得更远。
对于冒充攻击,给定目标的图像集合 I t I^t It,每个迭代选择一个四元组 q u a d k = < x k o , x k + , x k − , t k > quad_k=<x_k^o,x_k^+,x_k^-,t_k> quadk=<xko,xk+,xk−,tk>,由 t r i k tri_k trik和从 I t I^t It中选择的 t k t_k tk组成。迭代地优化下面的问题:
argmax δ E q u a d k ∼ { X C , I t } f θ ( ( x k o ) ′ , t k ) + λ 1 f θ ( ( x k o ) ′ , ( x k + ) ′ ) − λ 2 f θ ( ( x k o ) ′ , ( x k − ) ′ ) (6) {\underset{\delta}{\operatorname{arg max}}}\mathbb{E}_{quad_k\sim \{X^C,I^t\}}f_\theta((x_k^o)',t_k)+\lambda_1 f_\theta((x_k^o)',(x_k^+)')-\lambda_2 f_\theta((x_k^o)',(x_k^-)')\tag{6} δargmaxEquadk∼{XC,It}fθ((xko)′,tk)+λ1fθ((xko)′,(xk+)′)−λ2fθ((xko)′,(xk−)′)(6)
其中 λ 1 \lambda_1 λ1和 λ 2 \lambda_2 λ2是控制不同目标的强度的超参数。
相关文章:

【论文笔记】advPattern
【论文题目】 advPattern: Physical-World Attacks on Deep Person Re-Identification via Adversarially Transformable Patterns Abstract 本文首次尝试对深度reID实施鲁棒的物理世界攻击。提出了一种新颖的攻击算法,称为advPattern,用于在衣服上生成…...
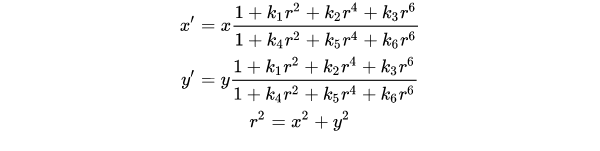
【鱼眼镜头11】Kannala-Brandt模型和Scaramuzza多项式模型区别,哪个更好?
Kannala-Brandt模型和Scaramuzza多项式模型在描述鱼眼相机畸变时都有其特定的数学表示和应用,但它们之间存在一些区别。以下是对两者区别的分点表示和归纳: 数学表示: Kannala-Brandt模型:它假设图像光心到投影点的距离和角度的多…...
微信小程序仿胖东来轮播和背景效果(有效果图)
效果图 .wxml <view class"swiper-index" style"--width--:{{windowWidth}}px;"><image src"{{swiperList[(cardCur bgIndex -1?swiperList.length - 1:cardCur bgIndex > swiperList.length -1?0:cardCur bgIndex)]}}" clas…...

10.SpringBoot 统一处理功能
文章目录 1.拦截器1.1在代码中的应用1.1.1定义拦截器1.1.2注册配置拦截器 1.2拦截器的作用1.3拦截器的实现 2.统一数据返回格式2.1 为什么需要统⼀数据返回格式?2.2 统⼀数据返回格式的实现 3.统一异常处理4.SpringBoot专业版创建项目无Java8版本怎么办?…...

【八股系列】为什么会有webpack配置?webpack的构建流程是什么?
文章目录 1. webpack是什么?2. 为什么需要webpack?3. webpack构建原理4. 构建流程通常包括以下步骤5. Webpack构建流程图 1. webpack是什么? Webpack是一个模块打包工具,它可以将项目中的各种静态资源,如JavaScript、…...

sdf 测试-2-openssl
任务详情 在openEuler(推荐)或Ubuntu或Windows(不推荐)中完成下面任务,参考网内容 和AI要给出详细过程,否则不得分。 0. 根据gmt0018标准,如何调用接口实现基于SM3求你的学号姓名的SM3值?(5‘) 使用OpenSSL实现SDF接…...

头歌springboot初体验
您好!看起来您可能在询问关于Spring Boot的入门体验。Spring Boot是一个开源的Java框架,它设计用来简化Spring应用程序的初始搭建和开发过程。以下是一些Spring Boot的基本概念和入门步骤: Spring Boot简介: Spring Boot是Spring框…...
矩阵对角化在机器学习中的奥秘与应用
在机器学习的广阔领域中,矩阵对角化作为一种重要的数学工具,扮演着不可或缺的角色。从基础的线性代数理论到复杂的机器学习算法,矩阵对角化都在其中发挥着重要的作用。 矩阵对角化的概念与原理 矩阵对角化是矩阵理论中的一个基本概念&#x…...

操作MySQL数据库
【一】针对库的增删查改(文件夹) 【1】创建数据库 (1)语法 创建一个存储数据表的文件夹。 注意:mysql中的编码字符集中utf-8,要换成utf8mb4。SQL语句中的中括号部分表示可选。 create database [if no…...
)
Linux shell 文件生成文件脚本(模拟生成文件、生成大量文件)
文章目录 Linux shell 文件生成文件脚本 Linux shell 文件生成文件脚本 TARGET_DIR:生成文件路径 NUM_FILES:生成文件数量 FILE_SIZE:生成文件大小(KB) #!/bin/bashset -e set -u# Directory where files will be cr…...

theharvester一键收集域名信息(KALI工具系列十)
目录 1、KALI LINUX简介 2、theharvester工具简介 3、在KALI中使用theharvester 3.1 用搜索引擎扫描 3.2 扫描并输出结果 3.3 扫描某域名下的所有账号 3.4 使用所有的搜索引擎扫描 4、总结 1、KALI LINUX简介 Kali Linux 是一个功能强大、多才多艺的 Linux 发行版&…...

「动态规划」删除并获得点数
力扣原题链接,点击跳转。 给你一个整数数组nums。每次操作,可以删除任意一个值n,接着获得点数n,并同时删除所有的n-1和n1。你最多能获取多少点数? 这个问题的解法相当巧妙。我们可以把问题先转化一下。用类似计数排序…...

MongoDB CRUD操作:内嵌文档数组查询
MongoDB 内嵌文档数组查询 文章目录 MongoDB 内嵌文档数组查询查询数组内嵌文档为文档数组中的字段指定查询条件指定文档数组内嵌文档字段的查询条件使用数组索引查询内嵌文档的字段 为文档数组指定多个条件单个内嵌文档满足内嵌字段的多个查询条件符合标准的元素组合 使用 Mon…...
)
【C++】每日一题 50 Pow(x,n)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x^n )。 当需要计算x的n次幂时,可以使用递归或者迭代的方式来实现。 #include <iostream>double myPow(double x, int n) {if (n 0) {return 1.0;} else if (…...

HG/T 6088-2022 透水道路用涂料检测
透水混凝土是指由水泥、矿物掺合料、骨料、外加剂及水等主要材料经拌合形成的,具有透水功能的混凝土材料,用于其表面的涂料称为透水道路用涂料。 HG/T 6088-2022透水道路用涂料检测项目: 测试指标 测试方法 有害物质限量 GB 38468 在容器…...

linux定时清理docker日志脚本
Linux 定时清理 Docker 日志的脚本与配置指南 在使用 Docker 容器化应用程序时,日志文件可能会迅速增长,占用大量磁盘空间。为了保持系统的稳定性和高效运行,定期清理 Docker 日志文件是必要的。本文将介绍如何编写一个 Linux 脚本来清理 Docker 日志文件,并通过 cron 定时…...
ROS学习笔记(16):夹缝循迹
0.前言 在笔记的第15期对巡墙驾驶的原理进行了简单讲解,而这期我们来讲一下夹缝循迹,也常被叫follow the gap,也更新一些概念。 1.探索式路径规划与避障 1.概念 无预先建图的路径规划叫探索式路径规划,例如巡墙循迹和夹缝循迹&…...
-锁和事务语句)
【MySQL精通之路】SQL语句(3)-锁和事务语句
目录 1.START TRANSACTION、COMMIT和ROLLBACK语句 2.无法回滚的语句 3.导致隐含COMMIT的语句 4.SAVEPOINT、ROLLBACK TO SAVEPOINT和RELEASE SAVEPOINT语句 5.LOCK INSTANCE FOR BACKUP和UNLOCK INSTANCE语句 6.LOCK TABLE和UNLOCK TABLES语句 6.1 表锁获取 6.2 表锁释放…...
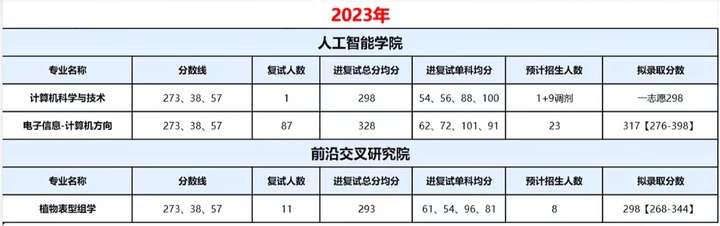
211大学计算机专业不考408,新增的交叉专业却考408!南京农业大学计算机考研考情分析!
南京农业大学信息科技学院可追溯至1981年成立的计算中心和1985年筹建的农业图书情报专业。1987年设立了农业图书情报系,1993 年农业图书情报系更名为信息管理系,本科专业名称也于1999年更名为信息管理与信息系统专业。1994年计算中心开始招收计算机应用专…...

利用java8 的 CompletableFuture 优化 Flink 程序,性能提升 50%
你好,我是 shengjk1,多年大厂经验,努力构建 通俗易懂的、好玩的编程语言教程。 欢迎关注!你会有如下收益: 了解大厂经验拥有和大厂相匹配的技术等 希望看什么,评论或者私信告诉我! 文章目录 一…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
