【ES001】elasticsearch实战经验总结(最近更新中)
相关文章:
)
【ES001】elasticsearch实战经验总结(最近更新中)
1.熟悉、梳理、总结下elasticsearch相关知识体系。 2.日常研发过程中使用较少,随着时间的推移,很快就忘得一干二净,所以梳理总结下,以备日常使用参考 3.欢迎批评指正,跪谢一键三连! 文章目录 1. 1....

OpenBayes 一周速览|TripoSR 开源:1 秒即 2D 变 3D、经典 GTZAN 音乐数据集上线
公共资源速递 This Weekly Snapshots !5 个数据集: FER2013 面部表情识别数据集 GTZAN 音乐流派分类数据集 MVTec-AD 工业异常检测数据集 UCAS-AOD 遥感目标检测数据集 Oxford 102 Flowers 花卉图片数据集 3 个教程: Latte 全球首个开…...
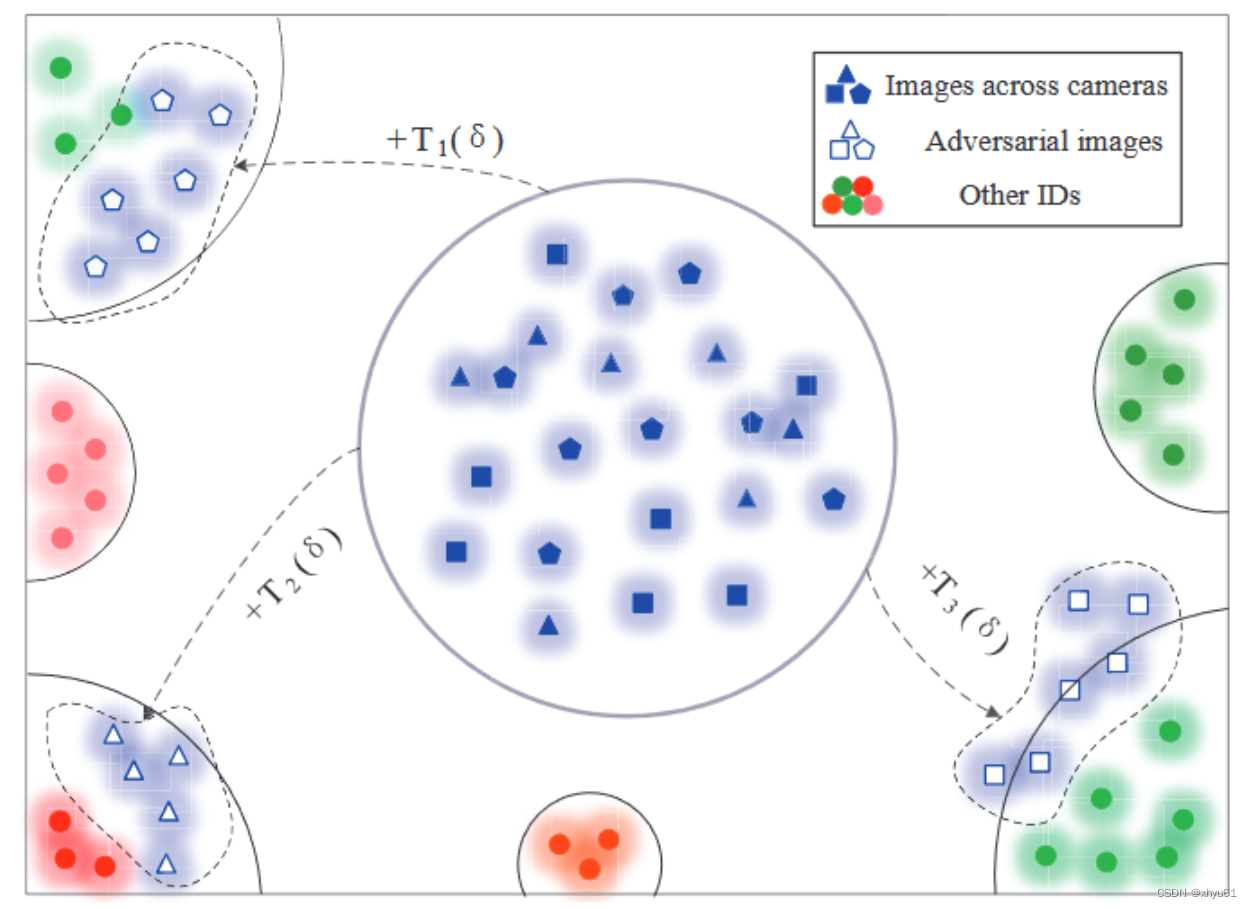
【论文笔记】advPattern
【论文题目】 advPattern: Physical-World Attacks on Deep Person Re-Identification via Adversarially Transformable Patterns Abstract 本文首次尝试对深度reID实施鲁棒的物理世界攻击。提出了一种新颖的攻击算法,称为advPattern,用于在衣服上生成…...
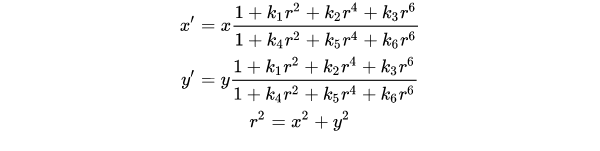
【鱼眼镜头11】Kannala-Brandt模型和Scaramuzza多项式模型区别,哪个更好?
Kannala-Brandt模型和Scaramuzza多项式模型在描述鱼眼相机畸变时都有其特定的数学表示和应用,但它们之间存在一些区别。以下是对两者区别的分点表示和归纳: 数学表示: Kannala-Brandt模型:它假设图像光心到投影点的距离和角度的多…...
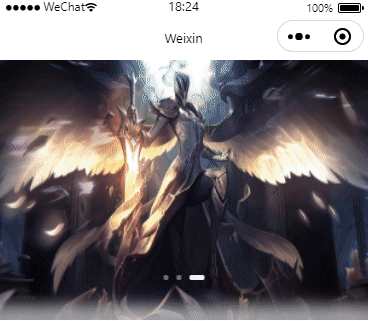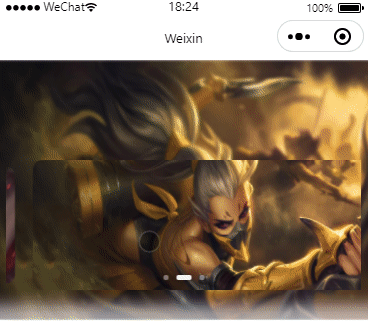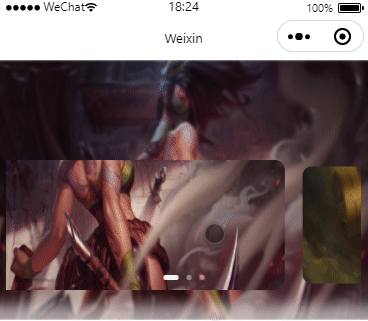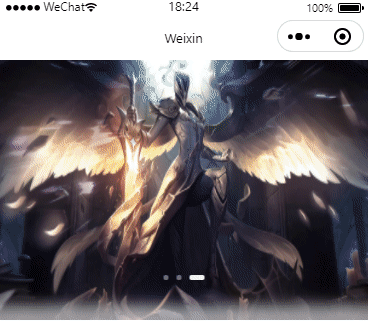
微信小程序仿胖东来轮播和背景效果(有效果图)
效果图 .wxml <view class"swiper-index" style"--width--:{{windowWidth}}px;"><image src"{{swiperList[(cardCur bgIndex -1?swiperList.length - 1:cardCur bgIndex > swiperList.length -1?0:cardCur bgIndex)]}}" clas…...

10.SpringBoot 统一处理功能
文章目录 1.拦截器1.1在代码中的应用1.1.1定义拦截器1.1.2注册配置拦截器 1.2拦截器的作用1.3拦截器的实现 2.统一数据返回格式2.1 为什么需要统⼀数据返回格式?2.2 统⼀数据返回格式的实现 3.统一异常处理4.SpringBoot专业版创建项目无Java8版本怎么办?…...

【八股系列】为什么会有webpack配置?webpack的构建流程是什么?
文章目录 1. webpack是什么?2. 为什么需要webpack?3. webpack构建原理4. 构建流程通常包括以下步骤5. Webpack构建流程图 1. webpack是什么? Webpack是一个模块打包工具,它可以将项目中的各种静态资源,如JavaScript、…...

sdf 测试-2-openssl
任务详情 在openEuler(推荐)或Ubuntu或Windows(不推荐)中完成下面任务,参考网内容 和AI要给出详细过程,否则不得分。 0. 根据gmt0018标准,如何调用接口实现基于SM3求你的学号姓名的SM3值?(5‘) 使用OpenSSL实现SDF接…...

头歌springboot初体验
您好!看起来您可能在询问关于Spring Boot的入门体验。Spring Boot是一个开源的Java框架,它设计用来简化Spring应用程序的初始搭建和开发过程。以下是一些Spring Boot的基本概念和入门步骤: Spring Boot简介: Spring Boot是Spring框…...
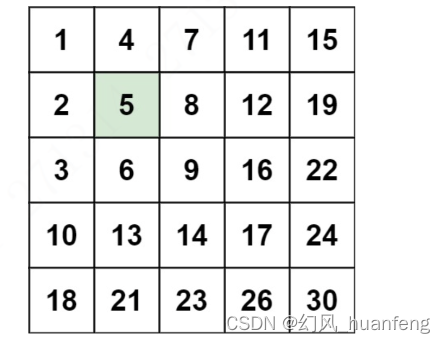
矩阵对角化在机器学习中的奥秘与应用
在机器学习的广阔领域中,矩阵对角化作为一种重要的数学工具,扮演着不可或缺的角色。从基础的线性代数理论到复杂的机器学习算法,矩阵对角化都在其中发挥着重要的作用。 矩阵对角化的概念与原理 矩阵对角化是矩阵理论中的一个基本概念&#x…...

操作MySQL数据库
【一】针对库的增删查改(文件夹) 【1】创建数据库 (1)语法 创建一个存储数据表的文件夹。 注意:mysql中的编码字符集中utf-8,要换成utf8mb4。SQL语句中的中括号部分表示可选。 create database [if no…...
)
Linux shell 文件生成文件脚本(模拟生成文件、生成大量文件)
文章目录 Linux shell 文件生成文件脚本 Linux shell 文件生成文件脚本 TARGET_DIR:生成文件路径 NUM_FILES:生成文件数量 FILE_SIZE:生成文件大小(KB) #!/bin/bashset -e set -u# Directory where files will be cr…...

theharvester一键收集域名信息(KALI工具系列十)
目录 1、KALI LINUX简介 2、theharvester工具简介 3、在KALI中使用theharvester 3.1 用搜索引擎扫描 3.2 扫描并输出结果 3.3 扫描某域名下的所有账号 3.4 使用所有的搜索引擎扫描 4、总结 1、KALI LINUX简介 Kali Linux 是一个功能强大、多才多艺的 Linux 发行版&…...

「动态规划」删除并获得点数
力扣原题链接,点击跳转。 给你一个整数数组nums。每次操作,可以删除任意一个值n,接着获得点数n,并同时删除所有的n-1和n1。你最多能获取多少点数? 这个问题的解法相当巧妙。我们可以把问题先转化一下。用类似计数排序…...

MongoDB CRUD操作:内嵌文档数组查询
MongoDB 内嵌文档数组查询 文章目录 MongoDB 内嵌文档数组查询查询数组内嵌文档为文档数组中的字段指定查询条件指定文档数组内嵌文档字段的查询条件使用数组索引查询内嵌文档的字段 为文档数组指定多个条件单个内嵌文档满足内嵌字段的多个查询条件符合标准的元素组合 使用 Mon…...
)
【C++】每日一题 50 Pow(x,n)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x^n )。 当需要计算x的n次幂时,可以使用递归或者迭代的方式来实现。 #include <iostream>double myPow(double x, int n) {if (n 0) {return 1.0;} else if (…...

HG/T 6088-2022 透水道路用涂料检测
透水混凝土是指由水泥、矿物掺合料、骨料、外加剂及水等主要材料经拌合形成的,具有透水功能的混凝土材料,用于其表面的涂料称为透水道路用涂料。 HG/T 6088-2022透水道路用涂料检测项目: 测试指标 测试方法 有害物质限量 GB 38468 在容器…...

linux定时清理docker日志脚本
Linux 定时清理 Docker 日志的脚本与配置指南 在使用 Docker 容器化应用程序时,日志文件可能会迅速增长,占用大量磁盘空间。为了保持系统的稳定性和高效运行,定期清理 Docker 日志文件是必要的。本文将介绍如何编写一个 Linux 脚本来清理 Docker 日志文件,并通过 cron 定时…...
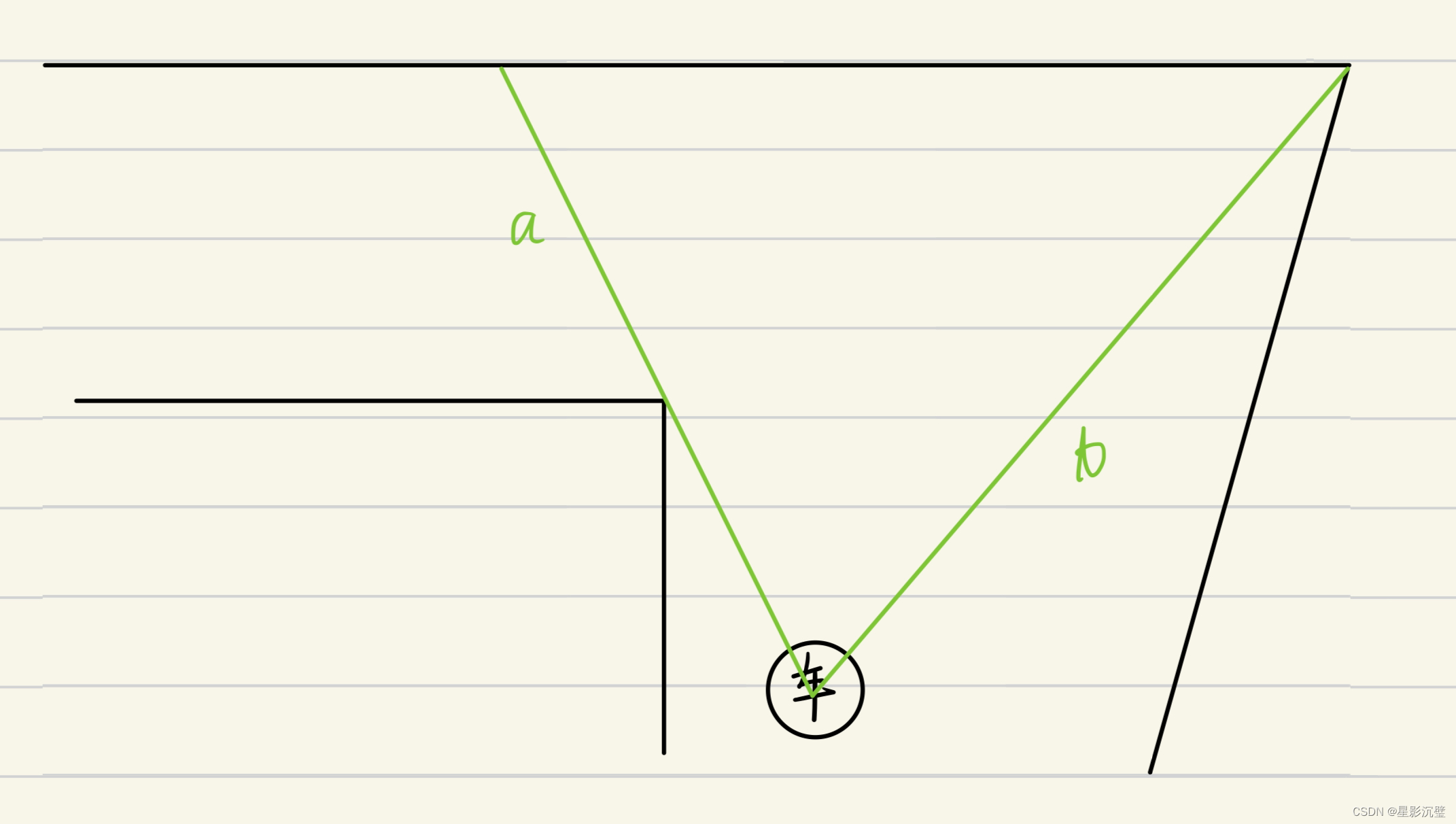
ROS学习笔记(16):夹缝循迹
0.前言 在笔记的第15期对巡墙驾驶的原理进行了简单讲解,而这期我们来讲一下夹缝循迹,也常被叫follow the gap,也更新一些概念。 1.探索式路径规划与避障 1.概念 无预先建图的路径规划叫探索式路径规划,例如巡墙循迹和夹缝循迹&…...
-锁和事务语句)
【MySQL精通之路】SQL语句(3)-锁和事务语句
目录 1.START TRANSACTION、COMMIT和ROLLBACK语句 2.无法回滚的语句 3.导致隐含COMMIT的语句 4.SAVEPOINT、ROLLBACK TO SAVEPOINT和RELEASE SAVEPOINT语句 5.LOCK INSTANCE FOR BACKUP和UNLOCK INSTANCE语句 6.LOCK TABLE和UNLOCK TABLES语句 6.1 表锁获取 6.2 表锁释放…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
