分布式事务解决方案(最终一致性【TCC解决方案】)
最终一致性分布式事务概述
强一致性分布式事务解决方案要求参与事务的各个节点的数据时刻保持一致,查询任意节点的数据都能得到最新的数据结果,这就导致在分布式场景,尤其是高并发场景下,系统的性能受到了影响。而最终一致性分布式事务解决方案并不要求参与事务的各个节点数据时刻保持一致,运行其存在中间状态,只要一段时间后,能够达到数据的最终一致状态即可,在电商场景中使用比较多
典型方案
业界基于Base理论提出的最终一致性分布式事务解决方案有:
- TCC解决方案
- 可靠消息最终一致性解决方案
- 最大努力通知型解决方案
优缺点
最终一致性分布式事务解决方案的优点:
- 性能比较高,这是因为最终一致性分布式事务解决方案不要求数据时刻保持一致,不会因为长时间持有事务占用的资源而过度消耗过多的性能
- 具备可用性
- 适合高并发场景
最终一致性分布式事务解决方案的缺点:
- 因为数据存在短暂的不一致,所以在某个时刻查询出的数据状态可能会不一致
- 对于事务一致性要求特别高的场景不适用
服务模式
- 可查询操作:需要服务操作具有可标识性,主要体现在服务的操作具有全局唯一的标识,可以是业务的单据编码(如订单号)也可以是系统分配的操作流水号,另外在可查询的服务模式中,也要有完整的操作时间信息
- 幂等性操作:指对同一个方法,只要参数相同,无论执行多少次都与第一次执行时产生的影响相同,为了保证数据的最终一致性,系统会提供很多次重试操作,这个时候就需要接口实现幂等性操作
- TCC操作:这个模式下包括了3个阶段,Try阶段(尝试业务执行)、Confirm阶段(确认业务阶段)和cancel阶段(取消业务执行)
Try阶段
- 完成所有业务的一致性检查
- 预留必要的业务资源,并需要与其他操作隔离
Confirm阶段
- 此阶段会真正执行业务操作
- 因为在Try阶段完成了业务的一致性检查,所有此阶段不会做任务业务检查
- 只用Try阶段预留的业务资源进行操作
- 此阶段的操作需要满足幂等性
Cancel阶段
- 释放Try阶段预留的业务资源
- 此阶段的操作需要满足幂等性
- 可补偿操作:某些数据处于不正常的状态,需要通过某种方式进行业务补偿,使数据能够达到最终一致性,这种因数据不正常而进行的补偿操作,就是可补偿操作服务模式
TCC解决方案
TCC是一种典型的解决分布式事务问题的方案,主要解决跨服务调用场景下得分布式事务问题,广泛应用于分布式事务场景
适用场景
用于具有强隔离性,严格一致性要的业务场景,也适用于执行时间比较短的业务,对于电商场景中下得减库存等业务,如果使用TCC分布式事务,则会经历Try、Confirm、Cancel三个阶段
需要实现的服务模式
在TCC分布式事务解决方案中,需要实现的服务模式包括TCC操作,幂等操作、可补偿操作、可查询操作。
例如实现TCC分布式事务方案时,需要实现Try、Confirm、Cancel三个阶段的业务逻辑,这就是TCC操作,在TCC操作的每个阶段的方法都需要实现幂等性,这就是幂等操作,如果在执行分布式事务过程中业务服务出现了异常情况,则需要支持重试阶段,以达到事务补偿的目的,这就是可补偿操作,另外业务服务需要提供可以查询自身内部事务状态的接口,以供其他服务调用,这就是可查询操作
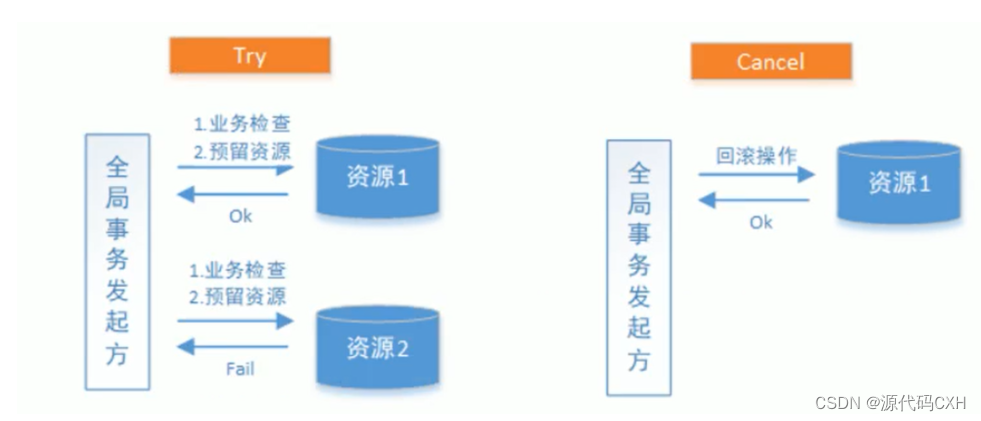
分支事务失败的情况:
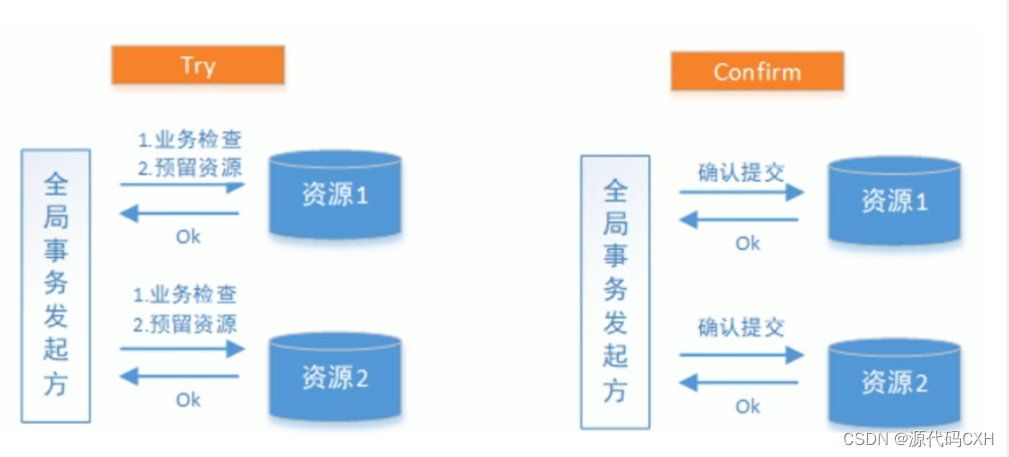
本质上讲,TCC是一种应用层实现的二阶段提交协议,TCC方案的执行流程如下
- Try阶段:不会执行任务业务逻辑,仅做业务的一致性检查和预留相应的资源,这些资源能够和其他操作保持隔离
- confirm阶段:当Try阶段所有分支事务执行成后开始执行Confirm阶段,通常情况下,采用TCC解决分布式事务时会任务Confirm阶段是不会出错的,也就是说,只要Try阶段的操作执行成功了,Confirm阶段就一定会执行成功,如果Confirm阶段出错了,就需要引入重试机制或者人工处理,对出错的事务进行干预
- Cancel阶段:在业务执行异常或出现错误的情况下,需要回滚事务的操作,执行分支事务的取消操作,并且释放Try阶段预留的资源,通常情况下,采用TCC方法解决分布式事务时,同样会认为Cacnel阶段也是一定会执行成功的,如果出现错误,就需要引入重试机制或者人工处理,对出错的事务进行干预
方案的优缺点
TCC方案的优点
- 在应用层实现具体的逻辑,锁定资源的粒度变小,不会锁定所有资源,提升了系统的性能
- Confirm阶段和Cancel阶段的方法具备幂等性,能够保证分布式事务执行完毕后数据的一致性
- TCC分布式解决方案有主业务发起整个事务,无论主业务还是分支事务所在的业务,都能部署为集群模式,从而解决了XA规范的单点故障问题
TCC方案的缺点
- 代码需要耦合到业务中,每个参与分布式事务的业务方法都要拆成Try、Confirm、Cancel三个阶段的方法,提高了开发的成本
需要注意的问题
使用TCC方案解决分布式事务问题时,需要注意空回滚、幂等和悬挂问题
空回滚问题
- 原因:出现空回滚的原因是一个分支事务所在的服务器宕机或者网络发生异常,此分支事务调用失败,此时并未执行此分支的Try阶段的方法,当服务器或者网络恢复后,TCC分布式事务执行回滚操作,会调用分支事务的Cancel阶段的方法,如果Cancel阶段的方法不能处理这种情况,就会出现空回滚的问题
- 解决方案:识别是否出现空回滚操作的方法是判断是否执行了Try阶段的方法,如果执行了Try阶段的方法,就没有空回滚,否则则出现空回滚
幂等问题
- 原因:由于服务器宕机、应用崩溃或者网络异常等原因,可能会出现方法调用超时的情况,为了保证方法的正常执行,往往会在TCC方案中加入超时重试机制,因为超时重试有可能导致数据的不一致问题,所以需要保证分支事务的执行以及TCC方案的Confirm阶段和Cancel阶段具备幂等性
- 解决方案:在分支事务记录表中增加事务的执行状态,每次执行分支事务以及Confirm阶段和Cancel阶段的方法时,都查询次事务的执行状态,以此判断事务的幂等性
悬挂问题
- 原因:TCC分布式事务中,通过RPC调用分支事务Try阶段的方法时,会先注册分支事务,在执行RPC调用。如果此时发生服务器宕机,应用崩溃或者网络异常等情况,RPC调用就会超时,如果RPC调用超时,事务管理器会通知对于的资源管理器回滚事务,可能资源管理器回滚完事务后,RPC请求达到了参与分支事务所在的业务方法,因为此时事务以及回滚,所以在Try阶段预留的资源就无法释放了,这种情况下,就成为悬挂
- 解决方案:如果执行了Confirm阶段或者Cancel阶段的方法,则Try阶段的方法就不能再执行了,具体方案是在执行Try阶段的方法时,判断分支记录表中是否存在同一全局事务下Confirm阶段或者Cancel阶段的事务记录,如果存在,则不执行Try阶段的方法
相关文章:

分布式事务解决方案(最终一致性【TCC解决方案】)
最终一致性分布式事务概述 强一致性分布式事务解决方案要求参与事务的各个节点的数据时刻保持一致,查询任意节点的数据都能得到最新的数据结果,这就导致在分布式场景,尤其是高并发场景下,系统的性能受到了影响。而最终一致性分布式…...
App Inventor 2 Encrypt.Security 安全性扩展:MD5哈希,SHA/AES/RSA/BASE64
这是关于App Inventor和Thunkable安全性的扩展,它提供MD5哈希,SHA1和SHA256哈希,AES加密/解密,RSA加密/解密,BASE64编码/解码方法。 权限 此扩展程序不需要任何权限。 事件 OnErrorOccured 抛出任何异常时将触发此事件…...

深入了解Linux中的环境变量
在Linux系统中,环境变量(Environment Variables)是用于配置操作系统和应用程序运行环境的一种机制。它们储存在键值对中,可以控制程序的行为、路径查找和系统配置。本文将深入探讨环境变量的基本概念、常见类型、设置和管理方法&a…...

雷军-2022.8小米创业思考-8-和用户交朋友,非粉丝经济;性价比是最大的诚意;新媒体,直播离用户更近;用真诚打动朋友,脸皮厚点!
第八章 和用户交朋友 2005年,为了进一步推动金山的互联网转型,让金山的同事更好地理解互联网的精髓,我推动了一场向谷歌学习的运动,其中一个小要求就是要能背诵“谷歌十诫”。 十诫的第一条就令人印象深刻:以用户为中…...
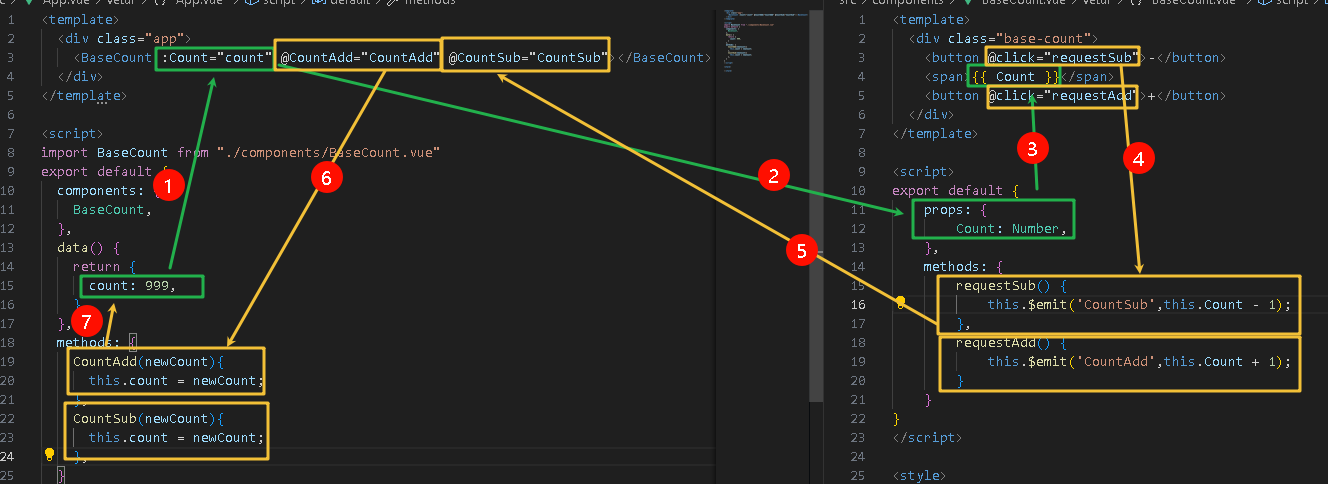
【Vue2.x】props技术详解
1.什么是prop? 定义:组件标签上注册的一些自定义属性作用:向子组件传递数据特点 可以传递任意数量的prop可以传递任意类型的prop 2.prop校验 为了避免乱传数据,需要进行校验 完整写法 将之前props数组的写法,改为对象…...

C语言例题46、根据公式π/4=1-1/3+1/5-1/7+1/9-1/11+…,计算π的近似值,当最后一项的绝对值小于0.000001为止
#include <stdio.h> #include <math.h>int main() {int fm 1;//分母double sign 1;//正负号double fzs 1;//分子式double sum 0;while (fabs(fzs) > 0.000001) {sum fzs;sign * -1; //变换正负号fm 2; //分母3、5、7、9...增长fzs sign / fm;//分子式…...
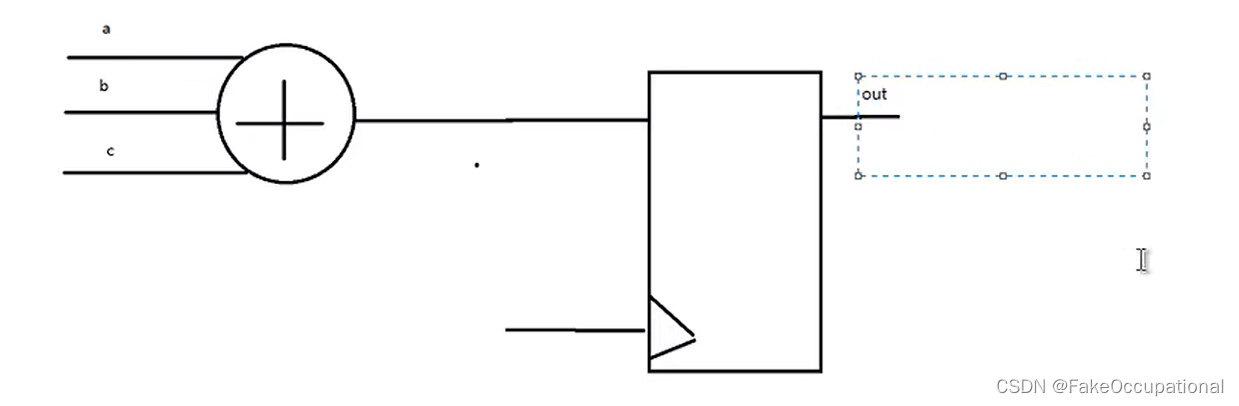
fpga系列 HDL: 05 阻塞赋值(=)与非阻塞赋值(<=)
在Verilog硬件描述语言(HDL)中,信号的赋值方式主要分为两种:连续赋值和过程赋值。每种赋值方式有其独特的用途和语法,并适用于不同类型的电路描述。 1. 连续赋值(Continuous Assignment,assign 和…...
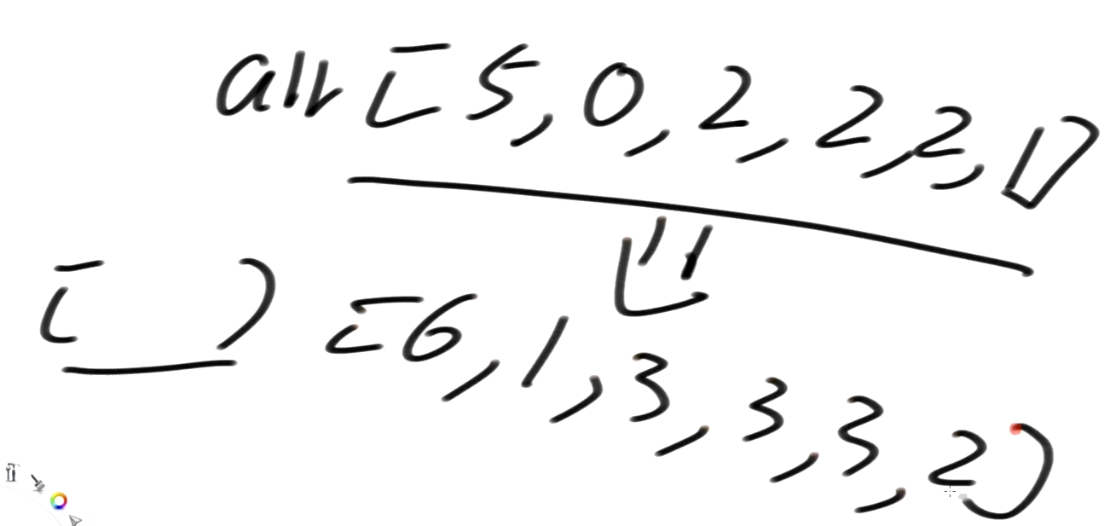
大白话DC3算法
DC3算法是什么 DC3算法(也称为Skew算法)是一种高效的构建后缀数组的算法,全称为Difference Cover Modulo 3算法。 该算法于2002年被提出,论文参考: https://www.cs.cmu.edu/~guyb/paralg/papers/KarkkainenSanders0…...

力扣HOT100 - 75. 颜色分类
解题思路: 单指针,对数组进行两次遍历。 class Solution {public void sortColors(int[] nums) {int p 0;int n nums.length;for (int i 0; i < n; i) {if (nums[i] 0) {int tmp nums[i];nums[i] nums[p];nums[p] tmp;p;}}for (int i p; i …...

Vue.js - 计算属性与侦听器 【0基础向 Vue 基础学习】
文章目录 计算属性 computedcomputed 的使用方法computed 与 method 的区别计算属性完整写法 watch 侦听器(监视器)简单写法 → 简单类型数据,直接监视完整写法 → 添加额外配置项 计算属性 computed computed 的使用方法 **概念࿱…...

技术速递|使用 C# 集合表达式重构代码
作者:David Pine 排版:Alan Wang 本文是系列文章的第二篇,该系列文章涵盖了探索 C# 12功能的各种重构场景。在这篇文章中,我们将了解如何使用集合表达式重构代码,我们将学习集合初始化器、各种表达式用法、支持的集合目…...
我的世界开服保姆级教程
前言 Minecraft开服教程 如果你要和朋友联机时,可以选择的方法有这样几种: 局域网联机:优点:简单方便,在MC客户端里自带。缺点:必须在同一局域网内。 有些工具会带有联机功能:优点:一…...
[转载]同一台电脑同时使用GitHub和GitLab
原文地址:https://developer.aliyun.com/article/893801 简介: 工作中我们有时可能会在同一台电脑上使用多个git账号,例如:公司的gitLab账号,个人的gitHub账号。怎样才能在使用gitlab与github时,切换成对应…...

【网络协议】【OSI】一次HTTP请求OSI工作过程详细解析
目录 1. 一次HTTP请求OSI工作过程 1.1 应用层(第7层) 1.2 表示层(第6层) 1.3 会话层(第5层) 1.4 传输层(第4层)...

springboot vue 开源 会员收银系统 (2) 搭建基础框架
前言 完整版演示 前面我们对会员系统https://blog.csdn.net/qq_35238367/article/details/126174288进行了分析 确定了技术选型 和基本的模块 下面我们将从 springboot脚手架开发一套收银系统 使用脚手架的好处 不用编写基础的rabc权限系统将工作量回归业务本身生成代码 便于…...

Java进阶学习笔记26——包装类
包装类: 包装类就是把基本类型的数据包装成对象。 看下API文档: deprecated:极力反对、不赞成的意思。 marked for removal:标识为去除的意思。 自动装箱:基本数据类型可以自动转换成包装类。 自动拆箱:…...

【JavaEE进阶】——要想代码不写死,必须得有spring配置(properties和yml配置文件)
目录 本章目标: 🚩配置文件 🚩SpringBoot配置文件 🎈配置⽂件的格式 🎈 properties 配置⽂件说明 📝properties语法格式 📝读取配置文件 📝properties 缺点分析 dz…...

第十四 Elasticsearch介绍和安装
docker-compose安装 kibana: image: docker.elastic.co/kibana/kibana:7.5.1 container_name: kibana ports: - "5601:5601" environment: ELASTICSEARCH_HOSTS: http://elasticsearch:9200 depends_on: - elasticsearch…...
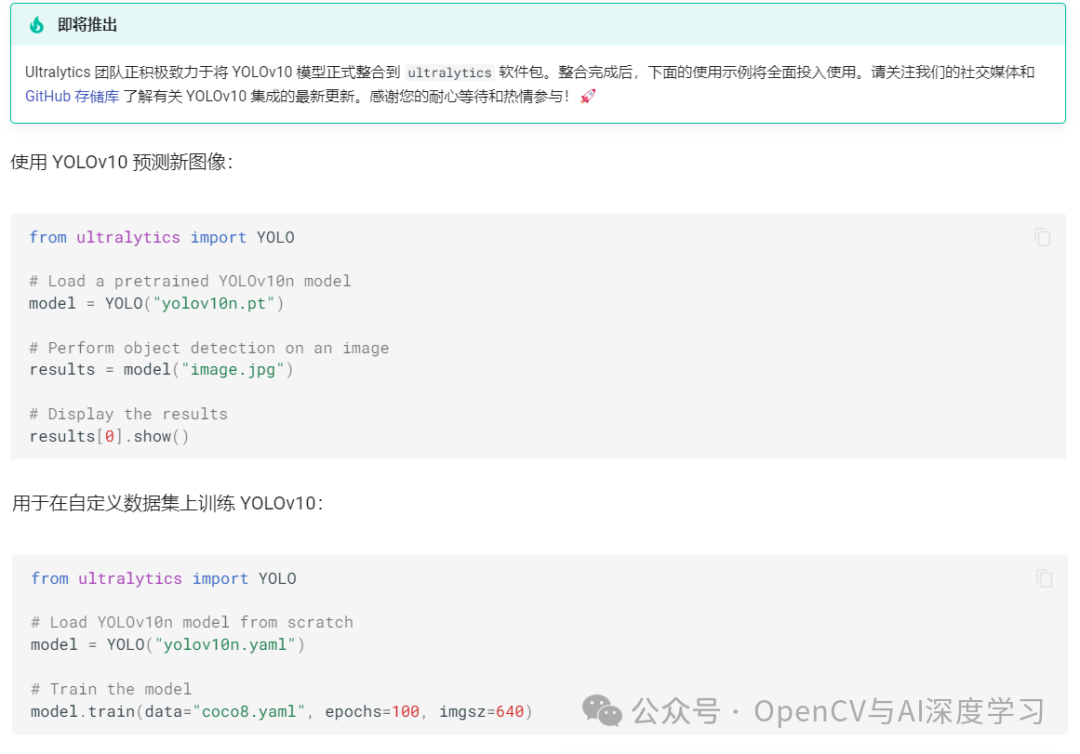
YOLOv10介绍与推理--图片和视频演示(附源码)
导 读 本文主要对YOLOv10做简单介绍并给出推理图片和视频的步骤演示。 YOLOv10简介 YOLOv10是清华大学的研究人员在Ultralytics Python包的基础上,引入了一种新的实时目标检测方法,解决了YOLO 以前版本在后处理和模型架构方面的不足。通过消除非最大抑…...

Java实验08
实验一 demo.java package q8.demo02;public class demo{public static void main(String[] args) {WindowMenu win new WindowMenu("Hello World",20,30,600,290);} }WindowMenu.java package q8.demo02; import javax.swing.*;public class WindowMenu extends…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
