算法刷题day54:搜索(一)
目录
- 引言
- 一、池塘计数
- 二、城堡问题
- 三、山峰和山谷
- 四、迷宫问题
- 五、武士风度的牛
- 六、抓住那头牛
- 七、矩阵距离
- 八、魔板
引言
针对于蓝桥杯,搜索问题还是非常之重要的,在省赛前深知暴搜的重要性,所以提前先把提高课的搜索一章给看了,结果省赛时用到的算法很少,几乎是没有,反而是刚学一两个星期的暴搜给了我很大的作用,全部题目几乎都用的是暴搜,所以对于 O I OI OI 赛制来说,暴搜的技巧还是很重要的,其实到了国赛也是很重要,听说国赛题都很难,而且有的题都是假题,所以说对于这种题,暴搜就显得更重要了,听说全打暴力就能国三,再对个一两道题目说不定就能国二,其实暴搜大部分样例跟全做出来没啥区别,只要你剪枝剪的好,就能多对几个样例,还是要多练,加油!
一、池塘计数
标签:BFS、Flood Fill
思路:其实就是一个找连通块的题目,只不过是一个八连通的,把 B F S BFS BFS 里的循环和方向变为对应的八个方向即可。具体的做法就是,遍历每一个格子,如果该格子没有被访问过,并且是一个池塘,就用 B F S BFS BFS 把这个池塘全部访问,然后结果加一,最后输出结果。
题目描述:
农夫约翰有一片 N∗M 的矩形土地。最近,由于降雨的原因,部分土地被水淹没了。现在用一个字符矩阵来表示他的土地。每个单元格内,如果包含雨水,则用”W”表示,如果不含雨水,则用”.”表示。现在,约翰想知道他的土地中形成了多少片池塘。每组相连的积水单元格集合可以看作是一片池塘。每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。请你输出共有多少片池塘,即矩阵中共有多少片相连的”W”块。输入格式
第一行包含两个整数 N 和 M。接下来 N 行,每行包含 M 个字符,字符为”W”或”.”,用以表示矩形土地的积水状况,字符之间没有空格。输出格式
输出一个整数,表示池塘数目。数据范围
1≤N,M≤1000
输入样例:
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
输出样例:
3
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010, M = N, INF = 0x3f3f3f3f;int n, m;
char g[N][N];
bool st[N][N];int dir[8][2] = {-1,-1, -1,0, -1,1, 0,-1, 0,1, 1,-1, 1,0, 1,1};void bfs(PII S)
{st[S.x][S.y] = true;queue<PII> q; q.push(S);while(q.size()){auto t = q.front(); q.pop();for(int i = 0; i < 8; ++i){int x = t.x + dir[i][0];int y = t.y + dir[i][1];if(x < 0 || x >= n || y < 0 || y >= m) continue;if(st[x][y] || g[x][y] == '.') continue;st[x][y] = true;q.push({x,y});}}
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 0; i < n; ++i) cin >> g[i];int res = 0;for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){if(!st[i][j] && g[i][j] == 'W'){res++;bfs({i,j});}}}cout << res << endl;return 0;
}
二、城堡问题
标签:BFS
思路:这道题要求的是连通块的个数,以及连通块中最大的那个。不一样的是,该题的限制变成了每一个房间都会有墙,也就是说能不能向某一个方向移动就看该方向是否有墙,一般这种拿数字代表墙的都是二进制位来表示的,只要把对应方向和该二进制位对应起来,拿位运算就知道该方向是否有墙,然后就是正常操作了,每找一个点就给该连通块数加一,返回总数即可。
题目描述:
1 2 3 4 5 6 7 #############################1 # | # | # | | ######---#####---#---#####---#2 # # | # # # # ##---#####---#####---#####---#3 # | | # # # # ##---#########---#####---#---#4 # # | | | | # ##############################(图 1)# = Wall | = No wall- = No wall方向:上北下南左西右东。
图1是一个城堡的地形图。请你编写一个程序,计算城堡一共有多少房间,最大的房间有多大。城堡被分割成 m∗n个方格区域,每个方格区域可以有0~4面墙。注意:墙体厚度忽略不计。输入格式
第一行包含两个整数 m 和 n,分别表示城堡南北方向的长度和东西方向的长度。接下来 m 行,每行包含 n 个整数,每个整数都表示平面图对应位置的方块的墙的特征。每个方块中墙的特征由数字 P 来描述,我们用1表示西墙,2表示北墙,4表示东墙,8表示南墙,P 为该方块包含墙的数字之和。例如,如果一个方块的 P 为3,则 3 = 1 + 2,该方块包含西墙和北墙。城堡的内墙被计算两次,方块(1,1)的南墙同时也是方块(2,1)的北墙。输入的数据保证城堡至少有两个房间。输出格式
共两行,第一行输出房间总数,第二行输出最大房间的面积(方块数)。数据范围
1≤m,n≤50,0≤P≤15
输入样例:
4 7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13
输出样例:
5
9
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 55, M = N, INF = 0x3f3f3f3f;int n, m;
int g[N][N];
bool st[N][N];int dir[4][2] = {0,-1, -1,0, 0,1, 1,0}; // 对应方向 int bfs(PII S) // 找出每个连通块内的块数
{st[S.x][S.y] = true;int res = 1;queue<PII> q; q.push(S);while(q.size()){auto t = q.front(); q.pop();for(int i = 0; i < 4; ++i){// 注意这里是从 t 走的if(g[t.x][t.y] >> i & 1) continue; // 刚好用与运算与之对应方向int x = t.x + dir[i][0];int y = t.y + dir[i][1];if(x < 0 || x >= n || y < 0 || y >= m) continue;if(st[x][y]) continue;res++;st[x][y] = true;q.push({x,y}); } }return res;
} int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m; // 不要被变量名所骗,要看具体含义for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){cin >> g[i][j];}}int sum = 0, maxv = 0;for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){if(!st[i][j]){int t = bfs({i,j});sum++;maxv = max(maxv, t);}}}cout << sum << endl << maxv << endl;return 0;
}
三、山峰和山谷
标签:BFS、Flood Fill
思路:这道题问山峰和山谷的数量,其实就是遍历每一个连通块(高度相同),然后遍历的同时,看看周围有没有比它更高的或者更低的,如果没有比他高的那就是山峰,如果没有比它低的,那就是山谷,如果两个都没有那就都是,刚好也满足题目的要求。有一个细节,就是判断的是周围,所以只要不越界就都要判断一下,所以不必先判断是否能走,应最后判断。
题目描述:
FGD小朋友特别喜欢爬山,在爬山的时候他就在研究山峰和山谷。为了能够对旅程有一个安排,他想知道山峰和山谷的数量。给定一个地图,为FGD想要旅行的区域,地图被分为 n×n 的网格,每个格子 (i,j) 的高度 w(i,j) 是给定的。若两个格子有公共顶点,那么它们就是相邻的格子,如与 (i,j) 相邻的格子有(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1)
,(i+1,j),(i+1,j+1)。我们定义一个格子的集合 S 为山峰(山谷)当且仅当:S 的所有格子都有相同的高度。S 的所有格子都连通。对于 s 属于 S,与 s 相邻的 s′ 不属于 S,都有 ws>ws′(山峰),或者 ws<ws′(山谷)。如果周围不存在相邻区域,则同时将其视为山峰和山谷。你的任务是,对于给定的地图,求出山峰和山谷的数量,如果所有格子都有相同的高度,那么整个地图即是山峰,又是山谷。输入格式
第一行包含一个正整数 n,表示地图的大小。接下来一个 n×n 的矩阵,表示地图上每个格子的高度 w。输出格式
共一行,包含两个整数,表示山峰和山谷的数量。数据范围
1≤n≤1000,0≤w≤109
输入样例1:
5
8 8 8 7 7
7 7 8 8 7
7 7 7 7 7
7 8 8 7 8
7 8 8 8 8
输出样例1:
2 1
输入样例2:
5
5 7 8 3 1
5 5 7 6 6
6 6 6 2 8
5 7 2 5 8
7 1 0 1 7
输出样例2:
3 3
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010, M = N, INF = 0x3f3f3f3f;int n, m;
int g[N][N];
bool st[N][N];
int high, low;int dir[8][2] = {-1,-1, -1,0, -1,1, 0,-1, 0,1, 1,-1, 1,0, 1,1};void bfs(PII S)
{st[S.x][S.y] = true;bool has_higher = false, has_lower = false;queue<PII> q; q.push(S);while(q.size()){auto t = q.front(); q.pop();for(int i = 0; i < 8; ++i){int x = t.x + dir[i][0];int y = t.y + dir[i][1];if(x < 0 || x >= n || y < 0 || y >= n) continue; // 先判断是否越界if(g[x][y] > g[t.x][t.y]) has_higher = true; // 判断周围if(g[x][y] < g[t.x][t.y]) has_lower = true;if(st[x][y] || g[x][y] != g[t.x][t.y]) continue; // 判断是否为连通块st[x][y] = true;q.push({x,y});}}if(!has_higher) high++; // 没有比它高的if(!has_lower) low++; // 没有比他低的
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){cin >> g[i][j];}}for(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){if(!st[i][j]){bfs({i,j});}}}cout << high << " " << low << endl;return 0;
}
四、迷宫问题
标签:BFS
思路:这道题问的是一个最短的路径,其实针对于 B F S BFS BFS 来说第一次走过的点,就是该点的最短路径,我们只要在遍历的时候,把要更新的点的前驱记下来即可。因为路径是从起点开始,我们可以直接从后向前遍历,这样在推导的时候就可以顺便打印了。
题目描述:
给定一个 n×n 的二维数组,如下所示:int maze[5][5] = {0, 1, 0, 0, 0,0, 1, 0, 1, 0,0, 0, 0, 0, 0,0, 1, 1, 1, 0,0, 0, 0, 1, 0,};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角
的最短路线。数据保证至少存在一条从左上角走到右下角的路径。输入格式
第一行包含整数 n。接下来 n 行,每行包含 n 个整数 0 或 1,表示迷宫。输出格式
输出从左上角到右下角的最短路线,如果答案不唯一,输出任意一条路径均可。按顺序,每行输出一个路径中经过的单元格的坐标,左上角坐标为 (0,0),右下角坐标为 (n−1,n−1)。数据范围
0≤n≤1000
输入样例:
5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
0 0
1 0
2 0
2 1
2 2
2 3
2 4
3 4
4 4
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010, M = N, INF = 0x3f3f3f3f;int n, m;
int g[N][N];
bool st[N][N];
PII pre[N][N]; int dir[4][2] = {0,1,0,-1,1,0,-1,0};void bfs()
{st[n-1][n-1] = true;queue<PII> q; q.push({n-1,n-1});while(q.size()){auto t = q.front(); q.pop();if(t.x == 0 && t.y == 0) return;for(int i = 0; i < 4; ++i){int x = t.x + dir[i][0];int y = t.y + dir[i][1];if(x < 0 || x >= n || y < 0 || y >= n) continue;if(st[x][y] || g[x][y] == 1) continue;st[x][y] = true;pre[x][y] = {t.x,t.y};q.push({x,y});}}
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){cin >> g[i][j];}}bfs();PII start = {0,0}, end = {n-1,n-1};while(start != end){cout << start.x << " " << start.y << endl;start = pre[start.x][start.y];}cout << end.x << " " << end.y << endl;return 0;
}
五、武士风度的牛
标签:搜索、广度优先搜索、BFS
思路:这道题首先要看清楚行列,不一定是按顺序给你的,所以要小心,然后就是只不过搜索的时候把方式变了,其实本质上还是行列的一个变化而已,然后就是正常的求最短路。
最短路注意要点: 1. 输入的行列顺序 2. 起始点有时就是障碍 3. 起点有时是终点 4. 终点的符号跟正常的符号不一样
题目描述:
农民 John 有很多牛,他想交易其中一头被 Don 称为 The Knight 的牛。这头牛有一个独一无二的超能力,在农场里像 Knight 一样地跳(就是我们熟悉的象棋中马的走法)。虽然这头神奇的牛不能跳到树上和石头上,但是它可以在牧场上随意跳,我们把牧场用一个 x,y 的坐标图来表示。这头神奇的牛像其它牛一样喜欢吃草,给你一张地图,上面标注了 The Knight 的开始位置,树、灌木、石头以及其它障碍的位置,
除此之外还有一捆草。现在你的任务是,确定 The Knight 要想吃到草,至少需要跳多少次。The Knight 的位置用 K 来标记,障碍的位置用 * 来标记,草的位置用 H 来标记。这里有一个地图的例子:11 | . . . . . . . . . .10 | . . . . * . . . . . 9 | . . . . . . . . . . 8 | . . . * . * . . . . 7 | . . . . . . . * . . 6 | . . * . . * . . . H 5 | * . . . . . . . . . 4 | . . . * . . . * . . 3 | . K . . . . . . . . 2 | . . . * . . . . . * 1 | . . * . . . . * . . 0 ----------------------1 0 1 2 3 4 5 6 7 8 9 0
The Knight 可以按照下图中的 A,B,C,D… 这条路径用 5 次跳到草的地方(有可能其它路线的长度也是 5):11 | . . . . . . . . . .10 | . . . . * . . . . .9 | . . . . . . . . . .8 | . . . * . * . . . .7 | . . . . . . . * . .6 | . . * . . * . . . F<5 | * . B . . . . . . .4 | . . . * C . . * E .3 | .>A . . . . D . . .2 | . . . * . . . . . *1 | . . * . . . . * . .0 ----------------------10 1 2 3 4 5 6 7 8 9 0
注意: 数据保证一定有解。输入格式
第 1 行: 两个数,表示农场的列数 C 和行数 R。第 2..R+1 行: 每行一个由 C 个字符组成的字符串,共同描绘出牧场地图。输出格式
一个整数,表示跳跃的最小次数。数据范围
1≤R,C≤150
输入样例:
10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..
输出样例:
5
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 155, M = N, INF = 0x3f3f3f3f;int n, m;
char g[N][N];
int dist[N][N];
PII S, E;int dir[8][2] = {-2,-1, -2,1, -1,-2, -1,2, 1,-2, 1,2, 2,-1, 2,1};int bfs()
{if(g[S.x][S.y] == '*' || g[E.x][E.y] == '*') return false;memset(dist, -1, sizeof dist);dist[S.x][S.y] = 0;queue<PII> q; q.push(S);while(q.size()){auto t = q.front(); q.pop();if(t == E) return dist[t.x][t.y]; // 防止起点即终点for(int i = 0; i < 8; ++i){int x = t.x + dir[i][0];int y = t.y + dir[i][1];if(x < 0 || x >= n || y < 0 || y >= m) continue;if(dist[x][y] != -1 || g[x][y] == '*') continue; //=='*',因为起始点都不是'.' ,如果 != '.',访问不到终点dist[x][y] = dist[t.x][t.y] + 1;q.push({x,y}); }}return -1;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> m >> n; // 看清楚行列for(int i = 0; i < n; ++i) {cin >> g[i];for(int j = 0; j < m; ++j){if(g[i][j] == 'K') S = {i,j};if(g[i][j] == 'H') E = {i,j};}}cout << bfs() << endl;return 0;
}
六、抓住那头牛
标签:BFS
思路:这道题实际上跟上一题差不多,都是改变坐标,只不过这种方式第一次可能写不出来,但是看了一遍就会了,其余的也只是正常写法。这里说一下为什么小于零,或者大于两倍的 n n n 就非最优解,因为答案存在于 0 ∼ n 0\sim n 0∼n ,能走到零肯定是减到的,所以之后唯一的操作就是加,那就多余走了嘛。然后因为最多也只会走到这,再走明显就不如之前了。
题目描述:
农夫知道一头牛的位置,想要抓住它。农夫和牛都位于数轴上,农夫起始位于点 N,牛位于点 K。农夫有两种移动方式:从 X 移动到 X−1 或 X+1,每次移动花费一分钟从 X 移动到 2∗X,每次移动花费一分钟假设牛没有意识到农夫的行动,站在原地不动。农夫最少要花多少时间才能抓住牛?输入格式
共一行,包含两个整数N和K。输出格式
输出一个整数,表示抓到牛所花费的最少时间。数据范围
0≤N,K≤105
输入样例:
5 17
输出样例:
4
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 2e5+10, M = N, INF = 0x3f3f3f3f;int n, m;
int dist[N];int bfs()
{memset(dist, -1, sizeof dist);dist[n] = 0;queue<int> q; q.push(n);while(q.size()){int t = q.front(); q.pop();if(t == m) return dist[t];for(int i = 0; i < 3; ++i){int x;if(!i) x = t - 1;else if(i == 1) x = t + 1;else x = t * 2;if(x < 0 || x > N) continue; // 因为已经非最优解了if(dist[x] != -1) continue;dist[x] = dist[t] + 1;q.push(x); }}return -1;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;cout << bfs() << endl;return 0;
}
七、矩阵距离
标签:BFS、多源BFS
思路:这道题问的是所有的格子到 1 1 1 的最短距离,我们可以反过来从所有的 1 1 1 出发,去求到所有的距离,实际做法就是把所有的 1 1 1 入队,并把距离初始化为 0 0 0 ,然后跑一遍 B F S BFS BFS 。
题目描述:
给定一个 N 行 M 列的 01 矩阵 A,A[i][j] 与 A[k][l] 之间的曼哈顿距离定义为:dist(A[i][j],A[k][l])=|i−k|+|j−l|输出一个 N 行 M 列的整数矩阵 B,其中:B[i][j]=min1≤x≤N,1≤y≤M,A[x][y]=1dist(A[i][j],A[x][y])输入格式
第一行两个整数 N,M。
接下来一个 N 行 M 列的 01 矩阵,数字之间没有空格。输出格式
一个 N 行 M 列的矩阵 B,相邻两个整数之间用一个空格隔开。数据范围
1≤N,M≤1000
输入样例:
3 4
0001
0011
0110
输出样例:
3 2 1 0
2 1 0 0
1 0 0 1
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010, M = N, INF = 0x3f3f3f3f;int n, m;
char g[N][N];
int dist[N][N];int dir[4][2] = {0,1,0,-1,1,0,-1,0};void bfs()
{memset(dist, -1, sizeof dist);queue<PII> q;for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){if(g[i][j] == '1'){dist[i][j] = 0;q.push({i,j});}}}while(q.size()){auto t = q.front(); q.pop();for(int i = 0; i < 4; ++i){int x = t.x + dir[i][0];int y = t.y + dir[i][1];if(x < 0 || x >= n || y < 0 || y >= m) continue;if(dist[x][y] != -1) continue;dist[x][y] = dist[t.x][t.y] + 1;q.push({x,y});}}
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 0; i < n; ++i) cin >> g[i];bfs();for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){cout << dist[i][j] << " ";}cout << endl;}return 0;
}
八、魔板
标签:BFS
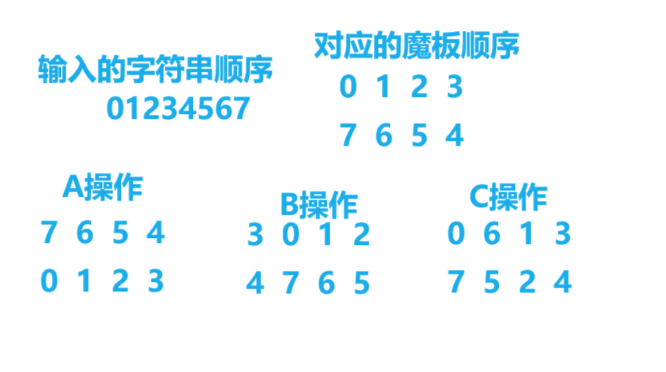
思路:其实就是状态的表示发生了变化,我用的是如下图的一个对应的顺序,其实这个表示方式不唯一,只要输入输出和变化一一对应即可。我这里面的数字都是下标,这样在变化的时候好理解。总的就是一个 B F S BFS BFS ,然后每次取出队头,进行三种变化,由于字典序最小,就按照 A B C ABC ABC 的顺序,然后有一个哈希表,存的是一对键值都是字符串,分别对应当前的状态,以及从起点到当前状态的操作方式,具体就跟 d i s t dist dist 的作用是一样的,还能用 c o u n t count count 方法来看这个状态是否访问过,根据操作方法的顺序来增加操作方法,然后就是具体的操作,我就是根据具体的下标变化,来赋值的。详情见代码,发现结构跟抓住那头牛是一模一样,只是状态和具体的操作不一样了而已。
题目描述:
Rubik 先生在发明了风靡全球的魔方之后,又发明了它的二维版本——魔板。这是一张有 8 个大小相同的格子的魔板:1 2 3 4
8 7 6 5
我们知道魔板的每一个方格都有一种颜色。这 8 种颜色用前 8 个正整数来表示。可以用颜色的序列来表示一种魔板状态,规定从魔板的左上角开始,沿顺时针方向依次取出整数,构成一个颜色序列。对于上图的魔板状态,我们用序列 (1,2,3,4,5,6,7,8) 来表示,这是基本状态。这里提供三种基本操作,分别用大写字母 A,B,C 来表示(可以通过这些操作改变魔板的状态):A:交换上下两行;
B:将最右边的一列插入到最左边;
C:魔板中央对的4个数作顺时针旋转。下面是对基本状态进行操作的示范:A:8 7 6 5
1 2 3 4
B:4 1 2 3
5 8 7 6
C:1 7 2 4
8 6 3 5
对于每种可能的状态,这三种基本操作都可以使用。你要编程计算用最少的基本操作完成基本状态到特殊状态的转换,输出基本操作序列。注意:数据保证一定有解。输入格式
输入仅一行,包括 8 个整数,用空格分开,表示目标状态。输出格式
输出文件的第一行包括一个整数,表示最短操作序列的长度。如果操作序列的长度大于0,则在第二行输出字典序最小的操作序列。数据范围
输入数据中的所有数字均为 1 到 8 之间的整数。输入样例:
2 6 8 4 5 7 3 1
输出样例:
7
BCABCCB
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1e5+10, M = N, INF = 0x3f3f3f3f;int n, m;
unordered_map<string,string> dist;
string S = "12345678", E;string dir = "ABC";string op1(string src)
{string res = src;for(int i = 0; i < 4; ++i){swap(res[i], res[7-i]);}return res;
}string op2(string src)
{string res = src;int t[8] = {3,0,1,2,5,6,7,4};for(int i = 0; i < 8; ++i){res[i] = src[t[i]];}return res;
}string op3(string src)
{string res = src;res[1] = src[6], res[2] = src[1];res[5] = src[2], res[6] = src[5];return res;
}string bfs()
{dist[S] = "";queue<string> q; q.push(S);while(q.size()){auto t = q.front(); q.pop();if(t == E) return dist[E];for(int i = 0; i < 3; ++i){string x;if(!i) x = op1(t);else if(i == 1) x = op2(t);else x = op3(t);if(dist.count(x)) continue;dist[x] = dist[t] + dir[i];q.push(x); }}return "impossible";
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);string t; while(cin >> t) E += t;string res = bfs();cout << res.size() << endl;if(res.size()) cout << res << endl;return 0;
}
相关文章:

算法刷题day54:搜索(一)
目录 引言一、池塘计数二、城堡问题三、山峰和山谷四、迷宫问题五、武士风度的牛六、抓住那头牛七、矩阵距离八、魔板 引言 针对于蓝桥杯,搜索问题还是非常之重要的,在省赛前深知暴搜的重要性,所以提前先把提高课的搜索一章给看了࿰…...

深入了解Redis的过期策略和内存淘汰机制
✨✨谢谢大家捧场,祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天开心哦!✨✨ 🎈🎈作者主页: 喔的嘛呀🎈🎈 ✨✨ 帅哥美女们,我们共同加油!一起进步&am…...

小白不知道怎么投稿?记住这个好方法
作为一名单位信息宣传员,我最初踏上这条道路时,满心憧憬着通过文字传递我们单位的精彩瞬间,让社会听见我们的声音。然而,理想与现实之间的距离,却在一次次邮箱投稿的石沉大海中渐渐清晰。那时的我,像所有“小白”一样,以为只要用心撰写稿件,通过电子邮件发给各大媒体,就能收获满…...

gRPC - Protocol Buffer 编译器安装
文章目录 Protocol Buffer 编译器安装如何安装 Protocol Buffer 编译器使用包管理器安装Linux 上,使用 apt 或 apt-get,例如:macOS 上,使用 Homebrew: 安装预编译的二进制文件(任何操作系统)其他…...

【Linux】centos7下载安装Python3.10,下载安装openssl1.1.1
目录 centos7下载安装Python(版本3.10.14) (1)网页下载python压缩包,并解压缩 (2)编译安装 Python在make altinstall时,报错及解决 (3)将安装目录和可执…...

通过 python 操作mongodb
库引入 Python 要连接 MongoDB 需要 MongoDB 驱动,这里我们使用 PyMongo 驱动来连接。 import pymongo 链接数据库 创建数据库需要使用 MongoClient 对象,并且指定连接的ip和端口号。 myclientpymongo.MongoClient("localhost",27017)#连接…...
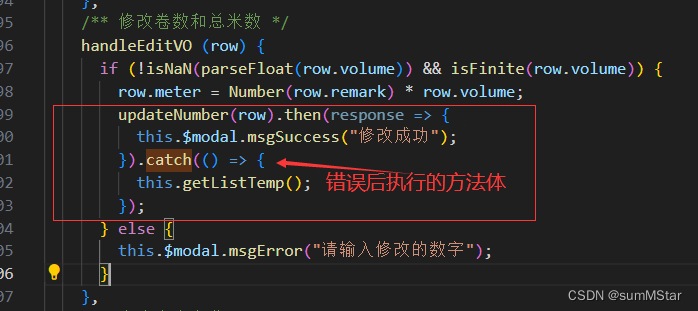
若依框架对于后端返回异常后怎么处理?
1、后端返回自定义异常serviceException 2、触发该异常后返回json数据 因为若依对请求和响应都封装了,所以根据返回值response获取不到Code值但若依提供了一个catch方法用来捕获返回异常的数据 3、处理的方法...
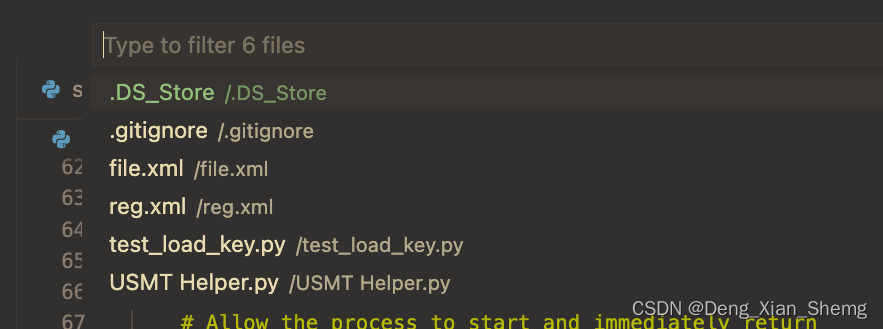
vs code怎么补全路径,怎么快捷输入文件路径
安装插件: 链接:https://marketplace.visualstudio.com/items?itemNamejakob101.RelativePath 使用 按住 Ctrl Shift H,弹出窗口,输入文件补全,回车就可以了 排除文件 如果你的项目下文件太多,它会…...

git分支开发主干合并流程
文章目录 一、分支开发二、主干合并三、删除合并过的分支 一、分支开发 创建分支git branch <分支名> # git branch my_new_branch开发后提交代码git commit -m 本次开发内容 # git commit -m 增加登录保持功能同步远端仓库git push origin <分支名> # git push o…...

01Python相关基础学习
Python基础 模块相关导入模块sys模块 模块相关 导入模块 1. import 模块名 2. import 模块名 as 别名 3. from 模块名 import 成员名 as 别名sys模块 1. sys.argv 介绍: 实现从程序的外部想程序传递参数返回的是一个列表,第一个元素是程序文件名,第二个元素是程序外部传入的…...

InTouch历史报警、历史事件按时段查询,导出
简介:本插件基于上位机组态InTouch的历史报警、操作记录而开发 适用InTouch版本:不限 适用Windows系统:不限 适用数据库:SQL Server 标记名点数:不限 配套软件安装:Excel、WPS、SQL Server 功能&…...

网络攻防概述(基础概念)
文章目录 APTAPT概念APT攻击过程 网络空间与网络空间安全网络空间(Cyberspace)网络空间安全(Cyberspace Security) 网络安全属性机密性(Confidentiality或Security)完整性(Integrity)可用性(Availability)不可否认性(Non-repudiation…...

了解Java垃圾收集
Java 的垃圾收集机制在 Java 应用程序开发中至关重要。此机制对于通过消除不再使用的对象来释放内存空间得过程来说至关重要。在这篇文章中,我带大家深入了解下 Java 垃圾收集的机制,并探索其工作原理、优点以及实现最佳性能的最佳实践。 1.什么是 Java…...

快速搭建 WordPress 外贸电商网站指南
本指南全面解析了在 Hostinger 平台上部署 WordPress 外贸电商网站的详细步骤,涵盖托管方案选择、WordPress 一键安装、主题挑选与演示数据导入、主题个性化定制、SEO插件插件 AIOSEO 安装、通过 GTranslate 实现多语言自动翻译、地区访问控制插件,助力用…...

网络编程 —— Http进度条
第一种下载带进度的方法 string url "https://nodejs.org/dist/v20.10.0/node-v20.10.0-x64.msi"; 1使用getASync获取服务器响应数据 参数1请求的路径, 参数2 HttpCompletionOption.ResponseHeadersRead 请求完成时候等待请求带什么程度才…...

5月26(信息差)
🌍 珠峰登顶“堵车”后冰架断裂 5人坠崖 2人没爬上来! 珠峰登顶“堵车”后冰架断裂 5人坠崖 2人没爬上来! 🎄 Windows 11 Beta 22635.3646 预览版发布:中国大陆地区新增“微软电脑管家”应用 ✨ 成都限购解除即将满…...
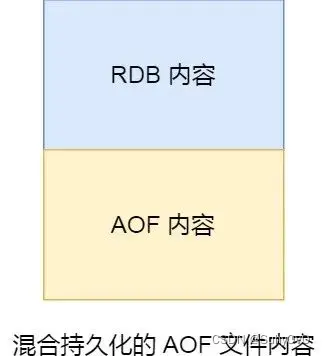
【Redis】持久化操作详解
Redis 持久化操作详解 Redis 实现持久化的时候,具体是按照什么样的策略来实现的呢? Redis支持两种方式的持久化,一种是RDB方式、另一种是AOF(append-only-file)方式,两种持久化方式可以单独使用其中一种&…...
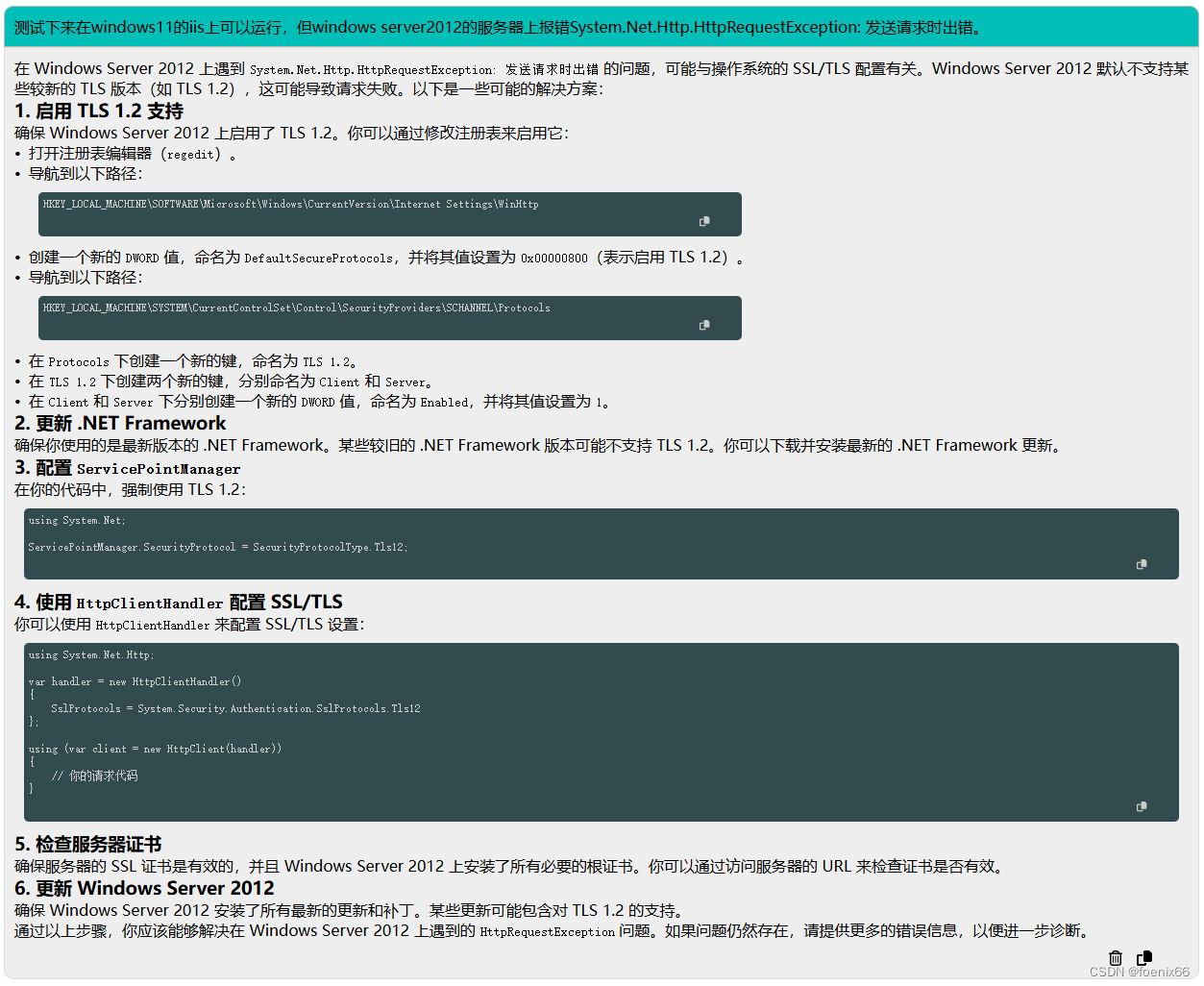
C#调用HttpClient.SendAsync报错:System.Net.Http.HttpRequestException: 发送请求时出错。
C#调用HttpClient.SendAsync报错:System.Net.Http.HttpRequestException: 发送请求时出错。 var response await client.SendAsync(request, HttpCompletionOption.ResponseHeadersRead, cancellationToken);问题出在SSL/TLS,Windows Server 2012不支持…...

大模型基础知识
文章目录 1. 位置编码1.1 绝对位置编码1.2 相对位置编码1.3 旋转位置编码2. 注意力机制2.1 MHA(muti head attention)2.2 MQA(muti query attention)2.3 GQA(grouped query attention)3. 大模型分类4. 微调方法4.1 Prompt Tuning4.2 Prefix Tuning4.3 Lora4.4 QLora5. La…...

时间序列预测模型实战案例(三)(LSTM)(Python)(深度学习)时间序列预测(包括运行代码以及代码讲解)
目录 引言 LSTM的预测效果图 LSTM机制 了解LSTM的结构 忘记门 输入门 输出门 LSTM的变体 只有忘记门的LSTM单元 独立循环(IndRNN)单元 双向RNN结构(LSTM) 运行代码 代码讲解 引言 LSTM(Long Short-Term Memory)是一种常用的循环神经网络&a…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...
