有限元法之有限元空间的构造
目录
一、区域Ω的剖分
二、三角形一次元
三、一次元的基函数与面积坐标
四、三角形二次元及其基函数
前两节我们介绍了有限元基本概念和变分理论的推导,本节我们继续探讨有限元空间的构造。
一、区域Ω的剖分
对矩形区域进行三角剖分,其中x方向剖分m份,y方向剖分n份,共得到
个节点及
个三角形单元。图1是
的剖分情况,节点编号用数字表示,单元用带圈的数字表示。为了实现后面的程序编写,必须明确单元上的局部编号与整体编号,如图2所示。通过设置剖分数,可以建立单元上整体编号与局部编号之间的关系,可设置二维数组
,第一个参数为单元编号,第二个参数为局部节点编号,如
等,表示第3个单元第0号局部节点的整体节点编号为8,而
则表示第2个单元第1号局部节点的整体节点编号为2。可以通过循环设置所有的节点。


二、三角形一次元
前面两节提到,可以选取为分片连续的一次多项式函数空间,也就是在每个单元e上,
中的函数都是一次多项式,且要保证整体连续。因此对于相邻的两个三角形单元,它们有一条公共边,只要保证分片一次多项式在这条公共边的两个端点(也是剖分节点)处函数值相同即可保证函数整体连续。这样,分片一次多项式在每个单元上的表达式就可以由它在3个顶点处的值唯一确定。下面,在节点
(对应整体编号为i,j,k)的单元e上考虑数值解
的表达式,尝试用基函数来表示
,其中
为待定基函数,满足以下性质:
且它们都是一次函数。这样,数值解在单元e上的表达式完全由它在3个顶点处
处的值
决定,
可以看作精确解u在整体编号i,j,k的节点处的近似。一旦把所有
求出来(边界点除外,因为
从而边界节点处
的值为零),则数值解
的表达式也就确定了。所以现在的基本问题是对离散问题式
求,使得
建立的关系式。
三、一次元的基函数与面积坐标
由于基函数在单元e上是一次多项式,尝试设,其中a,b,c为待定系数,且单元e上s号节点
的坐标为
,则由条件公式(1)可知:
从而解出
代入可得
可以证明以(逆时针排列)为顶点的三角形单元e的面积
。
于是,若内有一点P的坐标为
,如图3所示,则
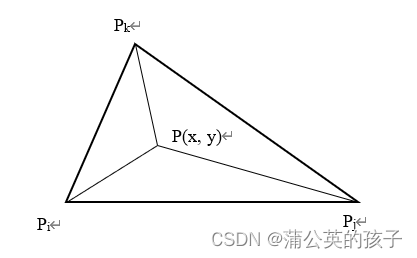
同理,
注意到,显然有
也就是说不是相互独立的。换言之,
内任一点
,必然可以唯一对应一组坐标
,基函数
被称为重心坐标。由于它们又都是三角形的面积比,所以它们也称为面积坐标。面积坐标在有限元分析中非常重要,它是从一般单元变化到标准单元的工具,也是进行Sobolev空间范数估计的有效手段。事实上,公式(4)、(5)可以反解出直角坐标
与重心坐标之间的对应关系式:
从而可以实现将一般的三角形单元变换成标准单元
,如图4所示。

四、三角形二次元及其基函数
我们除了可以选取为分片连续的一次多项式函数空间外,也可以选取
为分片连续的二次多项式函数空间,也就是在每个单元e上,
中的函数都是二次多项式,且要保证整体连续。因此在每个单元e上,
中的分片二次多项式函数
就形如
,其中
均为待定常数,从而需要有6个条件来唯一确定这个表达式。与一次元相似,要确定这6个常数,我们可以取三角形单元e的3个顶点及3条边的中点值作为条件(这些条件称为自由度),即分片二次多项式在每个单元上的表达式就可以由它在这个单元3个顶点和3条边的中点处的值唯一确定,这样也可以保证函数的整体连续性。事实上,在相邻的两个三角形单元上的公共边上,位置变量x和y有一个直线方程的线性约束,从而
在这条边上成为一个只关于自变量x的二次函数,这个函数在3个不同的点(两个顶点和一个中点)上取值相同,说明
在公共边上的表达式所示唯一确定的,也就是说,这个分片二次多项式在相邻两个单元上虽然整体表达式不相同,但在其公共边上表达式相同,这就保证了函数在
上整体连续,从而实现
。
对于以上的三角形二次元,由于涉及到三角形单元的中点,所以尽管三角形剖分情况不变,即共有2mn个三角形单元,但整体节点数变为个,且节点的编号将随之发生改变。例如,图1将变为图5。
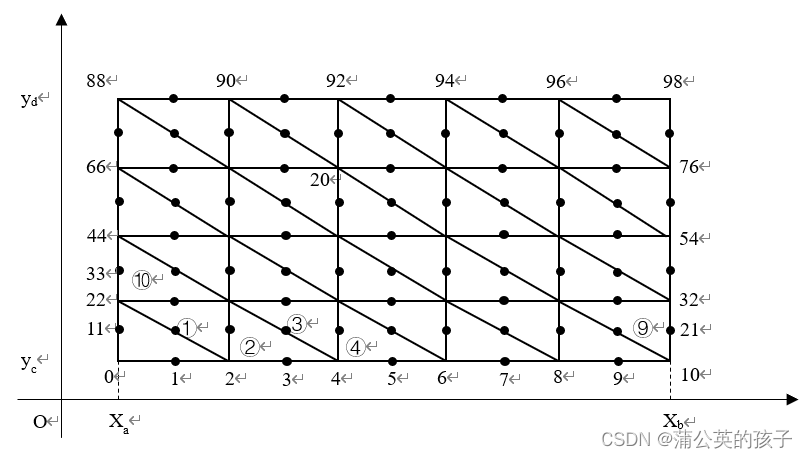
接下来,在单元e上考虑数值解的表达式,其中e的3个顶点为
(对应整体编号为i,j,k),3条边的中点为
(对应整体编号为
),如图6。
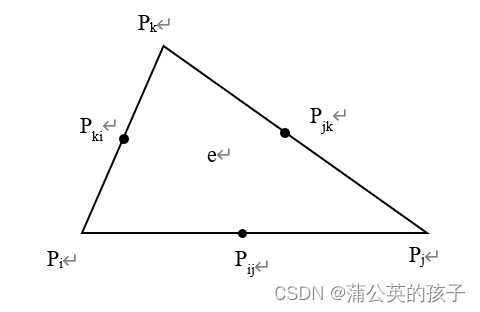
在单元e上的表达式尝试用基函数表示为
其中为待定基函数,满足以下性质:
利用重心坐标,很容易将上述基函数表示出来,即有分别对应于三角形单元3个顶点的基函数:
及对应于三角形3条边中点的 基函数:
至此,数值解 在单元e上的表达式就确定为:
综上,有限元空间由一个三元组
确定。具体的,设
是区域Ω的一个剖分,e是剖分
中的单元,参数h定义为所有单元的最大直径,即
,
是选定的分片多项式函数空间,
是每个e上用于唯一确定
内的多项式函数所需要的条件。
相关文章:
有限元法之有限元空间的构造
目录 一、区域Ω的剖分 二、三角形一次元 三、一次元的基函数与面积坐标 四、三角形二次元及其基函数 前两节我们介绍了有限元基本概念和变分理论的推导,本节我们继续探讨有限元空间的构造。 一、区域Ω的剖分 对矩形区域进行三角剖分,其中x方向剖…...

高通车规芯片分析
高通三款芯片 SA8155P 7nm SA8295P 5nm SA8255P 5nm 分析AECQ等级 AECQ100里面定义了5个工作环境温度等级:Grade0:-40-150 Grade1:-40-125 Grade2:-40-105 Grade3:-40-85 Grade4:0-70AEC-Q100整体认证测试…...

Flutter 中的 TextButton 小部件:全面指南
Flutter 中的 TextButton 小部件:全面指南 在Flutter的世界里,TextButton是一个基础的小部件,用于创建只包含文本的按钮。它通常用于对话框、表单以及需要强调主要操作的界面。本文将为您提供一个全面的指南,帮助您了解如何使用T…...

通过键值对访问字典
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 在Python中,如果想将字典的内容输出也比较简单,可以直接使用print()函数。例如,要想打印dictionary字典ÿ…...

海外仓扫码管理系统怎么选?精准,高效管理需求才是核心需求
海外仓对那些想拓展国际市场的商家来说还是非常重要的,大部分的货物都需要先运到海外仓,才能继续进行下一步的物流快递发货。 那对于海外仓本身来说,当面临大量订单的时候,怎么快速的管理订单,拣选货物就变得十分重要…...

基于51单片机的智能灯光控制系统
一.硬件方案 智能灯光控制系统由单片机最小系统、人体感应模块、关照强度模块、灯光控制模块、电源模块和灯泡组成。本文以STC89C52单片机为核心,通过利用光照度和红外人体感应相结合主动与被动的探测方法,现了室内无人或者关照充足时灯光自动光灯&…...

测试开发面试题
简述自动化测试的三大等待 强制等待。直接使用time.sleep()方法让程序暂停指定的时间。优点是实现简单,缺点是不够灵活,可能会导致不必要的等待时间浪费。隐式等待。设置一个固定的等待时间,在这个时间内不断尝试去查找元素,如果…...
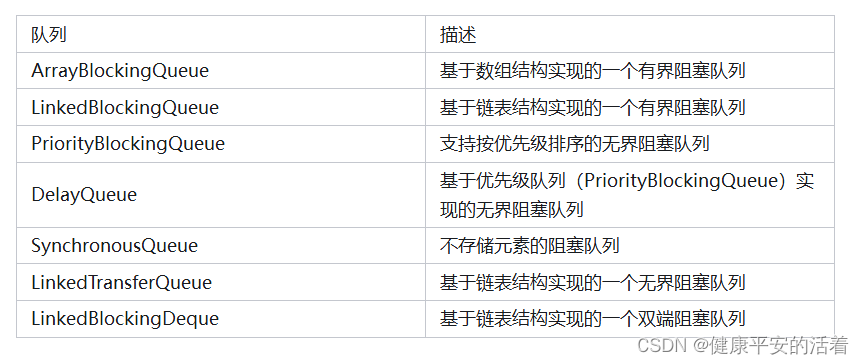
多线程JUC 第2季 BlockingQueue 阻塞队列
一 阻塞队列 1.1 阻塞队列介绍 阻塞队列(BlockingQueue)是一个在队列基础上又支持了两个附加操作的队列: put方法:当队列装满时,添加的线程则被阻塞,直到队列不满,则可用。 take方法&#x…...
-带查询扩展的全文搜索)
【MySQL精通之路】全文搜索(3)-带查询扩展的全文搜索
博主PS:你可以把他理解为,查询猜测,膨胀查询,查询的第六感。 全文搜索支持查询扩展(尤其是其变体“盲查询扩展”)。 当搜索短语太短时,这通常很有用,这通常意味着用户依赖于全文搜索…...
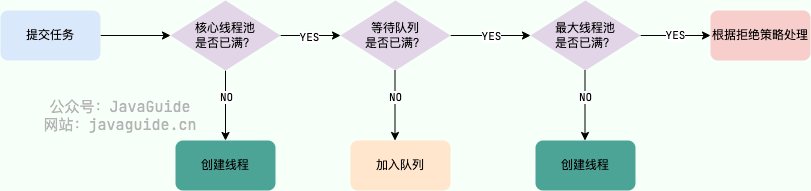
【面试必看】Java并发
并发 1. 线程 1. 线程vs进程 进程是程序的一次执行过程,是系统运行程序的基本单位,因此进程是动态的。 系统运行一个程序即是一个进程从创建,运行到消亡的过程。在 Java 中,当我们启动 main 函数时其实就是启动了一个 JVM 的进…...

C++的第一道门坎:类与对象(一)
1.面向过程与面向对象 1.1面向过程 我们之前学习的C语言就是一种面向过程的语言,面向过程的语言强调的是具体实现的过程,一般用函数来具体实现。我们用面向过程的思想,就可以把炒菜分为以下几个步骤: 1.2面向对象 而对于面向对象的语言而言…...

经典面试题:MySQL如何调优?
目录 前言1. SQL查询优化2. 索引优化3. 表结构设计4. 硬件与配置优化5. 日常维护6. 性能测试与基准测试 前言 MySQL如何进行调优?这是面试中容易被问到的高频问题。 1. SQL查询优化 避免使用select* :只选取需要的列,减少数据传输量。使用…...

【程序员如何送外卖】
嘿,咱程序员要在美团送外卖,那还真有一番说道呢。 先说说优势哈,咱程序员那逻辑思维可不是盖的,规划送餐路线什么的,简直小菜一碟。就像敲代码找最优解一样,能迅速算出怎么送最省时间最有效率。而且咱平时…...

【git pull 和 push详解】
git pull 和 push详解 1.背景2.命令和解释2.1 git pull简介详情 2.2 git push简介Git Push 参数及详细解释 1.背景 在分布式开发环境中,git pull和git push的使用确保了团队成员之间的代码一致性,减少了不同步导致的问题。它们简化了版本管理,…...

数据挖掘导致直接路径读(direct path read)耗尽了IO
一大早就有喊业务卡的,检查等待事件源头,均为oracle写等待 查看IO负载持续维持在100%繁忙 后台有两个并行rman备份在,停止备份io繁忙没有好转,检查最近ash报告,发现DDTEK ODBC Oracle程序模块占用最高 检查该模块&…...

用队列实现栈 用栈实现队列 设计循环队列
用队列实现栈 思路 栈的特点:后进先出 队列的特点:先进先出 使用两个队列实现栈: 我们可以使用两个队列,一个队列为:空队列,一个队列为:非空队列 当我们要出队列时: 将 size - …...

BFS解决最短路问题(详解)
目录 BFS简介 && 框架: 一.二叉树的最小深度 二:迷宫中里入口最近的出口: 三.最小基因变化: 四:单词接龙: 五:为高尔夫比赛砍树: BFS简介 && 框架: 说到BFS…...
按尺寸筛选轮廓图中的轮廓
1.按短边筛选 原始轮廓图: import cv2 import numpy as np# 读取轮廓图 contour_image cv2.imread(..\\IMGS\\pp_edge.png, cv2.IMREAD_GRAYSCALE)# 使用cv2.findContours()函数获取所有轮廓 contours, _ cv2.findContours(contour_image, cv2.RETR_EXTERNAL, cv2…...

VBA高级应用30例:实现在列表框内及列表框间实现数据拖动
《VBA高级应用30例》(版权10178985),是我推出的第十套教程,教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开,这套教程案例与理论结合,紧贴“实战”,并做“战术总结”,以…...

「AIGC算法」R-tree算法
R-tree算法是一种非常实用的空间数据索引技术,它可以帮助我们在复杂的空间数据中快速找到我们想要的信息。下面我将用一些生活中的例子来帮助大家更好地理解R-tree算法。 1. 定义与原理 想象一下,你有一个巨大的图书馆,里面有成千上万本书,每本书都有它在书架上的特定位置…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
