【简单介绍下线性回归模型】
🌈个人主页: 程序员不想敲代码啊
🏆CSDN优质创作者，CSDN实力新星，CSDN博客专家
👍点赞⭐评论⭐收藏
🤝希望本文对您有所裨益，如有不足之处，欢迎在评论区提出指正，让我们共同学习、交流进步！
🛸线性回归模型
🛸线性回归模型是一种用于建立变量之间线性关系的统计学模型，它假设自变量（输入）与因变量（输出）之间存在一个线性关系，通过寻找最佳拟合直线来预测因变量的值。线性回归模型的表达式可以写为：
🛸y = β0 + β1x1 + β2x2 + … + βn*xn + ε
🛸其中，y表示因变量，x1, x2, …, xn表示自变量，β0, β1, β2, …, βn表示模型的参数，ε表示误差项。
🛸在训练过程中，线性回归模型通过最小化实际观测值与模型预测值之间的误差（通常使用最小二乘法）来估计参数的值，从而找到最佳拟合直线，这使得我们可以使用该模型进行预测，并对自变量对因变量的影响进行解释。
🛸线性回归模型应用广泛，例如在经济学中用于预测房价、市场分析；在社会科学中用于研究人口统计数据等。但需要注意，线性回归模型对数据之间的线性关系假设较为严格，当数据存在非线性关系时，可能需要考虑其他类型的回归模型。
相关文章：
【简单介绍下线性回归模型】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者，CSDN实力新星，CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益，如有不足之处，欢迎在评论区提出指正，让我们共…...
有限元法之有限元空间的构造
目录 一、区域Ω的剖分 二、三角形一次元 三、一次元的基函数与面积坐标 四、三角形二次元及其基函数 前两节我们介绍了有限元基本概念和变分理论的推导，本节我们继续探讨有限元空间的构造。 一、区域Ω的剖分 对矩形区域进行三角剖分，其中x方向剖…...
高通车规芯片分析
高通三款芯片 SA8155P 7nm SA8295P 5nm SA8255P 5nm 分析AECQ等级 AECQ100里面定义了5个工作环境温度等级：Grade0：-40-150 Grade1：-40-125 Grade2：-40-105 Grade3：-40-85 Grade4：0-70AEC-Q100整体认证测试…...
Flutter 中的 TextButton 小部件：全面指南
Flutter 中的 TextButton 小部件：全面指南 在Flutter的世界里，TextButton是一个基础的小部件，用于创建只包含文本的按钮。它通常用于对话框、表单以及需要强调主要操作的界面。本文将为您提供一个全面的指南，帮助您了解如何使用T…...
通过键值对访问字典
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 在Python中，如果想将字典的内容输出也比较简单，可以直接使用print()函数。例如，要想打印dictionary字典ÿ…...
海外仓扫码管理系统怎么选？精准，高效管理需求才是核心需求
海外仓对那些想拓展国际市场的商家来说还是非常重要的，大部分的货物都需要先运到海外仓，才能继续进行下一步的物流快递发货。 那对于海外仓本身来说，当面临大量订单的时候，怎么快速的管理订单，拣选货物就变得十分重要…...
基于51单片机的智能灯光控制系统
一.硬件方案 智能灯光控制系统由单片机最小系统、人体感应模块、关照强度模块、灯光控制模块、电源模块和灯泡组成。本文以STC89C52单片机为核心，通过利用光照度和红外人体感应相结合主动与被动的探测方法，现了室内无人或者关照充足时灯光自动光灯&…...
测试开发面试题
简述自动化测试的三大等待 强制等待。直接使用time.sleep()方法让程序暂停指定的时间。优点是实现简单，缺点是不够灵活，可能会导致不必要的等待时间浪费。隐式等待。设置一个固定的等待时间，在这个时间内不断尝试去查找元素，如果…...
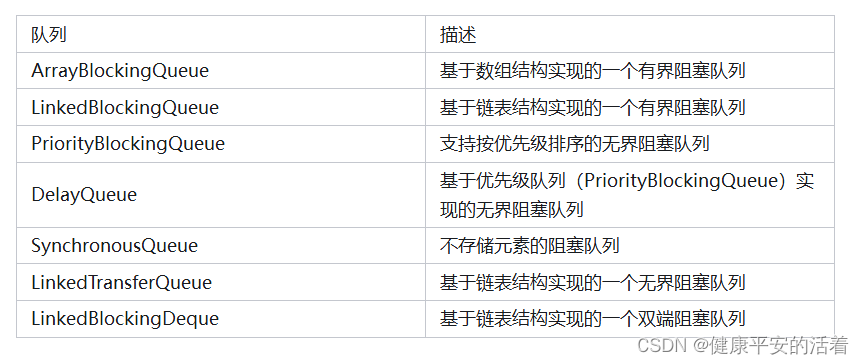
多线程JUC 第2季 BlockingQueue 阻塞队列
一 阻塞队列 1.1 阻塞队列介绍 阻塞队列（BlockingQueue）是一个在队列基础上又支持了两个附加操作的队列： put方法：当队列装满时，添加的线程则被阻塞，直到队列不满，则可用。 take方法&#x…...
-带查询扩展的全文搜索)
【MySQL精通之路】全文搜索(3)-带查询扩展的全文搜索
博主PS：你可以把他理解为，查询猜测，膨胀查询，查询的第六感。 全文搜索支持查询扩展（尤其是其变体“盲查询扩展”）。 当搜索短语太短时，这通常很有用，这通常意味着用户依赖于全文搜索…...
【面试必看】Java并发
并发 1. 线程 1. 线程vs进程 进程是程序的一次执行过程，是系统运行程序的基本单位，因此进程是动态的。 系统运行一个程序即是一个进程从创建，运行到消亡的过程。在 Java 中，当我们启动 main 函数时其实就是启动了一个 JVM 的进…...
C++的第一道门坎:类与对象（一）
1.面向过程与面向对象 1.1面向过程 我们之前学习的C语言就是一种面向过程的语言，面向过程的语言强调的是具体实现的过程，一般用函数来具体实现。我们用面向过程的思想，就可以把炒菜分为以下几个步骤: 1.2面向对象 而对于面向对象的语言而言…...
经典面试题：MySQL如何调优？
目录 前言1. SQL查询优化2. 索引优化3. 表结构设计4. 硬件与配置优化5. 日常维护6. 性能测试与基准测试 前言 MySQL如何进行调优？这是面试中容易被问到的高频问题。 1. SQL查询优化 避免使用select* ：只选取需要的列，减少数据传输量。使用…...
【程序员如何送外卖】
嘿，咱程序员要在美团送外卖，那还真有一番说道呢。 先说说优势哈，咱程序员那逻辑思维可不是盖的，规划送餐路线什么的，简直小菜一碟。就像敲代码找最优解一样，能迅速算出怎么送最省时间最有效率。而且咱平时…...
【git pull 和 push详解】
git pull 和 push详解 1.背景2.命令和解释2.1 git pull简介详情 2.2 git push简介Git Push 参数及详细解释 1.背景 在分布式开发环境中，git pull和git push的使用确保了团队成员之间的代码一致性，减少了不同步导致的问题。它们简化了版本管理，…...
数据挖掘导致直接路径读（direct path read）耗尽了IO
一大早就有喊业务卡的，检查等待事件源头，均为oracle写等待 查看IO负载持续维持在100%繁忙 后台有两个并行rman备份在，停止备份io繁忙没有好转，检查最近ash报告，发现DDTEK ODBC Oracle程序模块占用最高 检查该模块&…...
用队列实现栈 用栈实现队列 设计循环队列
用队列实现栈 思路 栈的特点：后进先出 队列的特点：先进先出 使用两个队列实现栈： 我们可以使用两个队列，一个队列为：空队列，一个队列为：非空队列 当我们要出队列时： 将 size - …...
BFS解决最短路问题(详解)
目录 BFS简介 && 框架： 一.二叉树的最小深度 二：迷宫中里入口最近的出口： 三.最小基因变化: 四：单词接龙： 五：为高尔夫比赛砍树： BFS简介 && 框架： 说到BFS…...
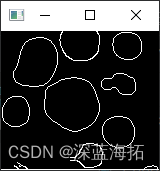
按尺寸筛选轮廓图中的轮廓
1.按短边筛选 原始轮廓图： import cv2 import numpy as np# 读取轮廓图 contour_image cv2.imread(..\\IMGS\\pp_edge.png, cv2.IMREAD_GRAYSCALE)# 使用cv2.findContours()函数获取所有轮廓 contours, _ cv2.findContours(contour_image, cv2.RETR_EXTERNAL, cv2…...
VBA高级应用30例：实现在列表框内及列表框间实现数据拖动
《VBA高级应用30例》（版权10178985），是我推出的第十套教程，教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开，这套教程案例与理论结合，紧贴“实战”，并做“战术总结”，以…...
应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间， 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点，不需要开启数据库闪回。…...
【人工智能】神经网络的优化器optimizer（二）：Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad（Adaptive Gradient Algorithm）是一种自适应学习率的优化算法，由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率，适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接：A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串，只有在同时为 o 时输出 Yes 并结束程序，否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...
R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
Git 3天2K星标：Datawhale 的 Happy-LLM 项目介绍（附教程）
引言 在人工智能飞速发展的今天，大语言模型（Large Language Models, LLMs）已成为技术领域的焦点。从智能写作到代码生成，LLM 的应用场景不断扩展，深刻改变了我们的工作和生活方式。然而，理解这些模型的内部…...
python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用： 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests：发送 …...
深度剖析 DeepSeek 开源模型部署与应用：策略、权衡与未来走向
在人工智能技术呈指数级发展的当下，大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性，吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型，成为释放其巨大潜力的关键所在&…...
java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用（Math::max） 2 函数接口…...
倒装芯片凸点成型工艺
UBM（Under Bump Metallization）与Bump（焊球）形成工艺流程。我们可以将整张流程图分为三大阶段来理解： 🔧 一、UBM（Under Bump Metallization）工艺流程（黄色区域ÿ…...
Python常用模块：time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的： 快速搭建小型Web服务器以提供数据。 工具： 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask： 建议： 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装，避免频繁切换。 PyCharm Terminal 配置建议： 打开 Py…...