朴素贝叶斯
经典三门问题
问题
一种说法(直觉派)
另一种说法(贝叶斯派)
注意P(B)=1, 已经知道路人抽中的就是绿豆
三门问题在网上争端比较大,分为直觉派和贝叶斯派,最后一个程序员出来写程序跑了一遍,发现就是贝叶斯派
朴素贝叶斯的直观理解
在X的条件下分别等于0~9的概率
注意之前我们讲的数据集是8*8的矩阵,然后我们处理矩阵的方式就是讲矩阵排列成一行
我们假设这个像素点的出现是相互独立的(在现实中并不是相互独立的)
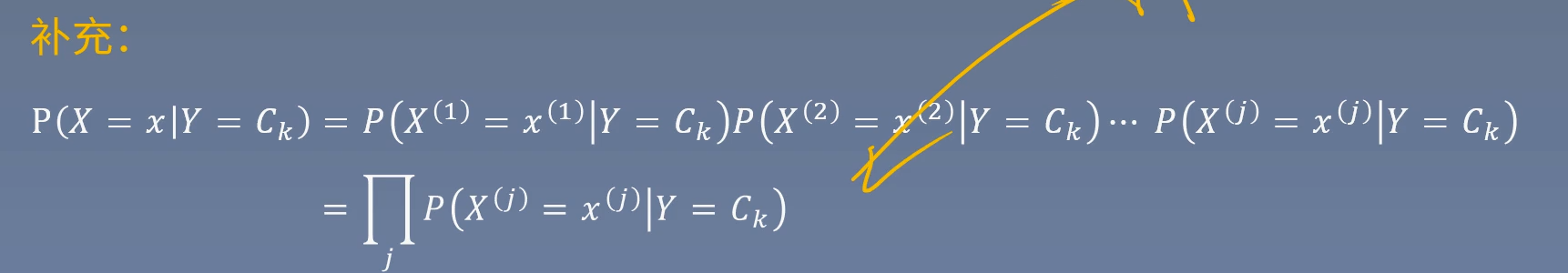
那个不太懂的点其实是Dodo讲错了,那里还是累乘的符号,然后64种情况累乘起来就是P(X=x),这是固定的,假设为C
所以求argmax就只用比较分子了
分子的比较涉及参数估计的知识
P(Y=CK)这是按照训练集0~9的个数来计算的,注意维度的区别,有些是像素维度,有些是图片维度
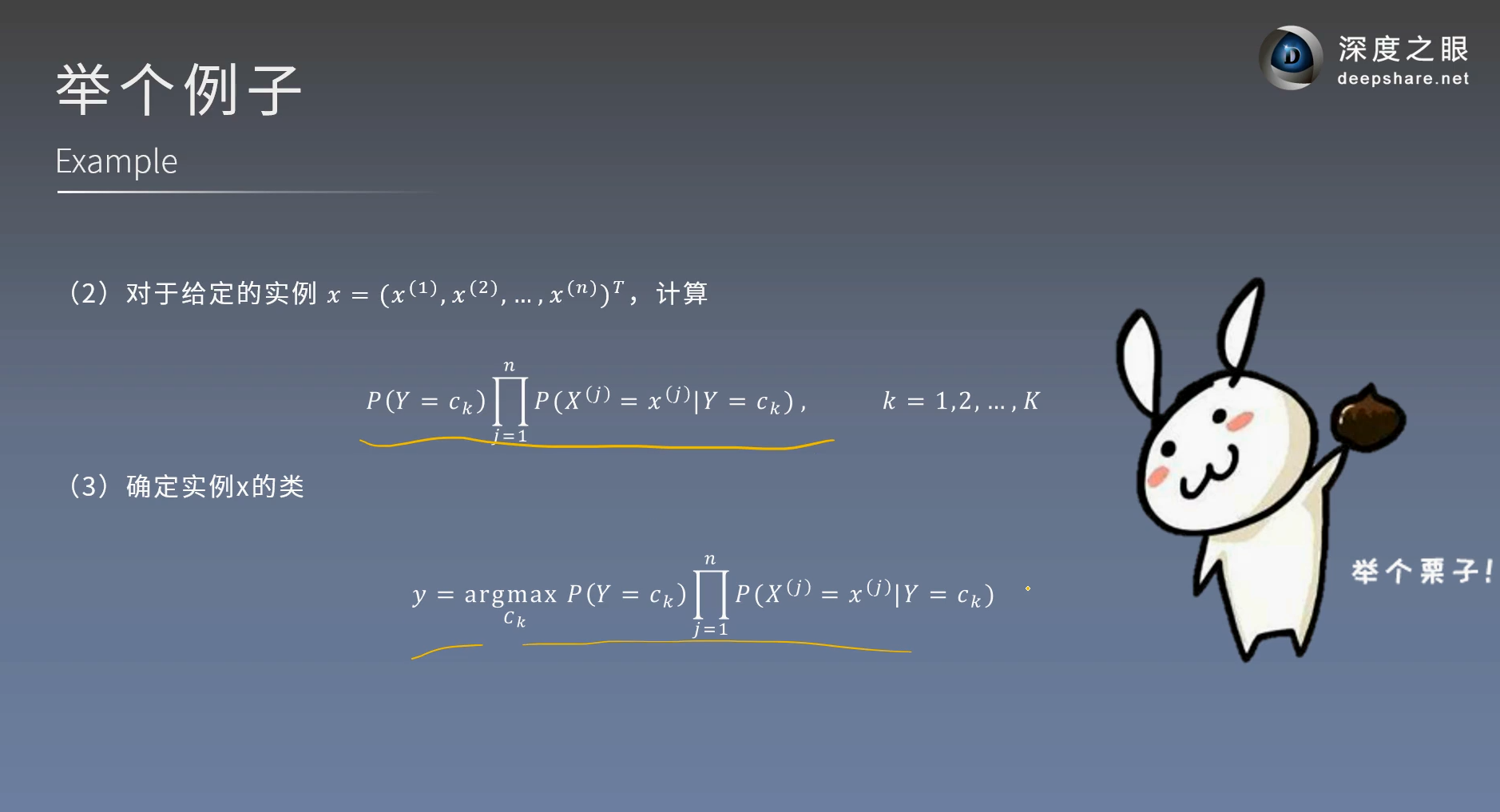
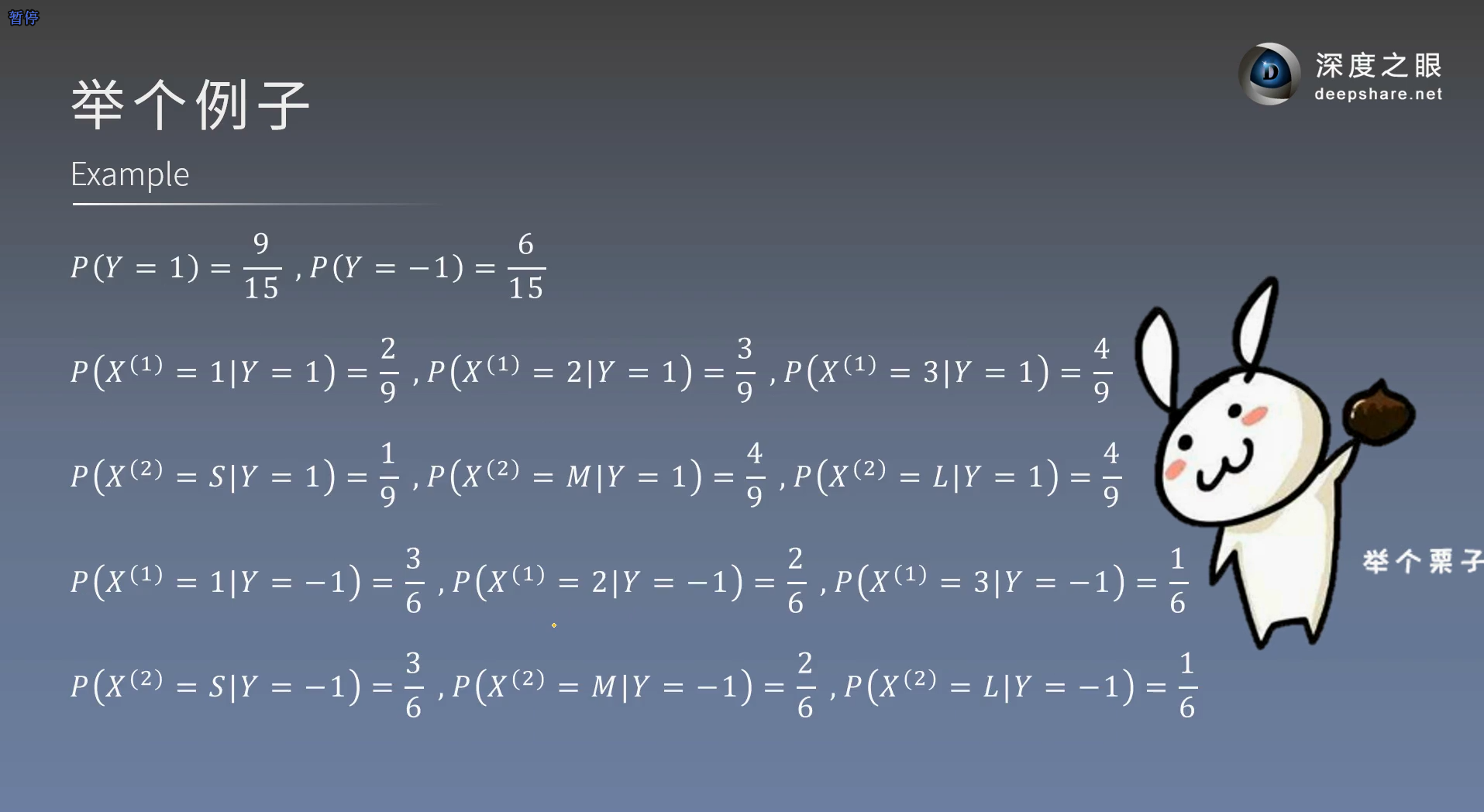
如果训练集中没有0,那么P(Y=CK)=0,就不能当分母了
贝叶斯估计
弥补前面分母为0的缺陷
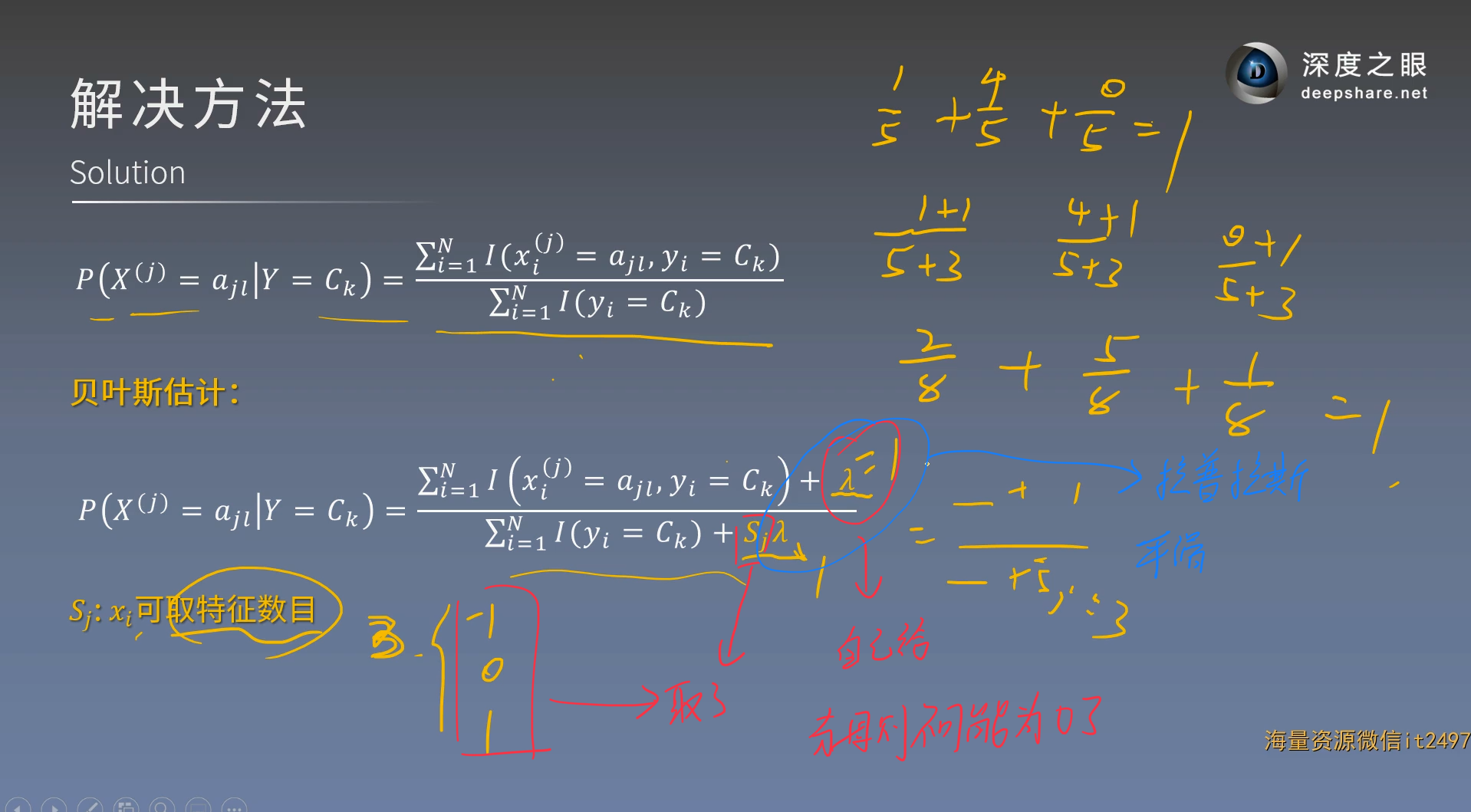
后验概率最大化(期望风险最小化)
下节预告
相关文章：
朴素贝叶斯
经典三门问题 问题 一种说法(直觉派) 另一种说法(贝叶斯派) 注意P(B)1, 已经知道路人抽中的就是绿豆 三门问题在网上争端比较大,分为直觉派和贝叶斯派,最后一个程序员出来写程序跑了一遍,发现就是贝叶斯派 朴素贝叶斯的直观理解 在X的条件下分别等于0~9的概率 注意之前我们讲的…...
【软件设计师】——10.面向对象技术
目录 10.1 基本概念 10.2设计原则 10.3 设计模式的概念与分类 10.4 创建型模式 10.4.1 Singleton 单例模式 10.4.2 Builder 构建器模式 10.4.3 Abstract Factory 抽象工厂模式 10.4.4 Prototype原型模式 10.4.5 Factory Method工厂方法模式 10.5 结构型模式 10.5.1 A…...
唐山无人机航拍，唐山无人机建模，唐山数据孪生
随着数字经济发展，各地逐渐兴起了无人机低空经济；尤其是无人机航拍，无人机建模；目前技术很成熟；比如水利部提出的数字孪生，四预的实现，都要通过无人机采集底层数据； 目前无人机建模…...
vue中分页查询的实现
在 Vue 中实现分页查询可以提升大型数据集的加载和显示效率。本文将逐步介绍如何使用 Vuex 状态管理和 axios HTTP 请求库来实现 Vue 分页查询。 1. 在 Vuex 中创建分页状态 首先，在 Vuex 状态管理中创建分页状态，该状态将存储每页的记录数、当前页码和…...
类 和 对象（二）
构造方法 接上篇，若每次都想下面的setDate方法给对象初始化，未免比较麻烦，那有什么方法可以让初始化更加简便呢？ public void setDate(int year, int month, int day){this.year year;this.month month;this.day day;}答&#…...
buu[HCTF 2018]WarmUp（代码审计）
buu[HCTF 2018]WarmUp（代码审计） 题目 访问source.php <?phphighlight_file(__FILE__);class emmm{public static function checkFile(&$page){$whitelist ["source">"source.php","hint">"hint.php…...
力扣爆刷第145天之图论五连刷（dfs和bfs）
力扣爆刷第145天之图论五连刷（dfs和bfs） 文章目录 力扣爆刷第145天之图论五连刷（dfs和bfs）总结一、797. 所有可能的路径二、200. 岛屿数量三、695. 岛屿的最大面积四、1020. 飞地的数量五、130. 被围绕的区域 总结 dfs是一条路走…...
Host头攻击-使用加密和身份验证机制
使用加密和身份验证机制，即安装合适的安全工具和软件，是确保Web服务器安全性的重要步骤。这种方法涉及使用各种安全工具来检测、预防、监控和响应潜在的安全威胁。以下是对第6种方法的详细讲解，包括一些常见的安全工具和软件的示例。 1. 防火…...
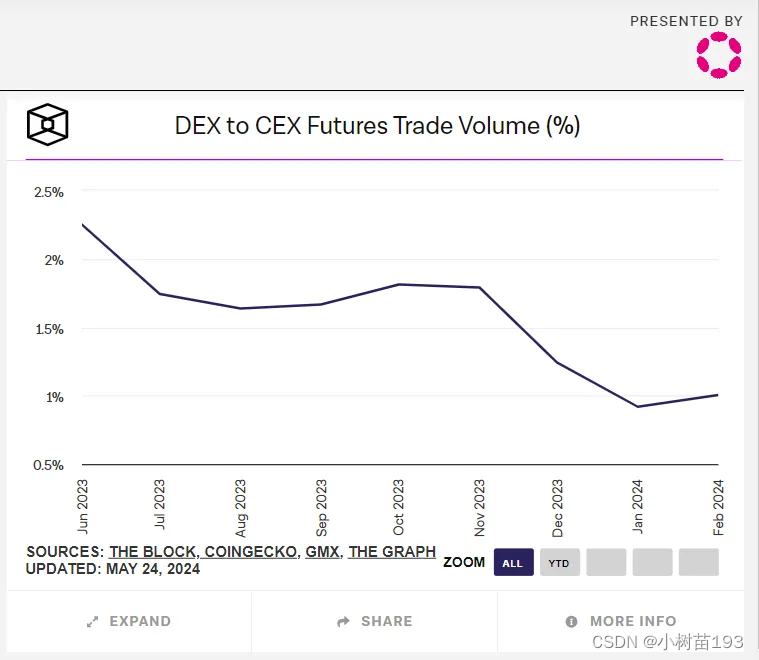
衍生品赛道的 UniSwap：SynFutures 或将成为行业领军者
经过一个周期的发展，DeFi 已经成为基于区块链构建的最成功的去中心化应用，并彻底改变了加密市场的格局。加密货币交易开始逐步从链下转移到链上，并从最初简单的 Swap 到涵盖借贷、Staking、衍生品交易等广泛的生态系统。 在 DeFi 领域&#x…...
TypeScript中的`let`、`const`、`var`区别：变量声明的规范与实践
TypeScript中的let、const、var区别：变量声明的规范与实践 引言 在TypeScript中，变量声明是代码编写的基础部分。let、const、var 是三种用于变量声明的关键字，它们各自有不同的作用域规则和可变性特点。 基础知识 作用域：变量…...
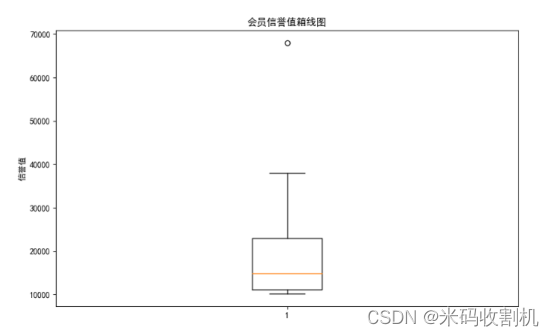
【python】python商家会员数据分析可视化（源码+数据集+课程报告论文）
👉博__主👈：米码收割机 👉技__能👈：C/Python语言 👉公众号👈：测试开发自动化【获取源码商业合作】 👉荣__誉👈：阿里云博客专家博主、5…...
Python限制输入的数范围
在Python中，我们可以使用多种方法来限制用户输入的数值范围。 1.使用while循环和try-except语句的方法 以下是一个使用while循环和try-except语句的示例，该示例将要求用户输入一个在指定范围内的整数。 假设我们要限制用户输入的数在1到100之间&#…...
postman都有哪些功能？
接口测试 可以方便地发送 HTTP 请求，包括各种方法（GET、POST、PUT、DELETE 等），并查看响应结果。 参数设置 能够灵活设置请求的参数，如查询参数、请求头、请求体等。 环境管理 支持创建不同的环境，方便…...
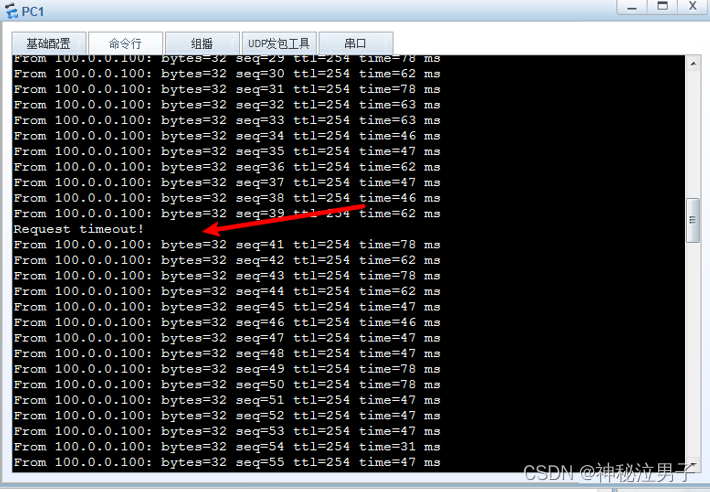
华为ensp中USG6000V防火墙双机热备VRRP+HRP原理及配置
作者主页：点击！ ENSP专栏：点击！ 创作时间：2024年5月6日20点26分 💯趣站推荐💯 前些天发现了一个巨牛的🤖人工智能学习网站，通俗易懂，风趣幽默，忍…...
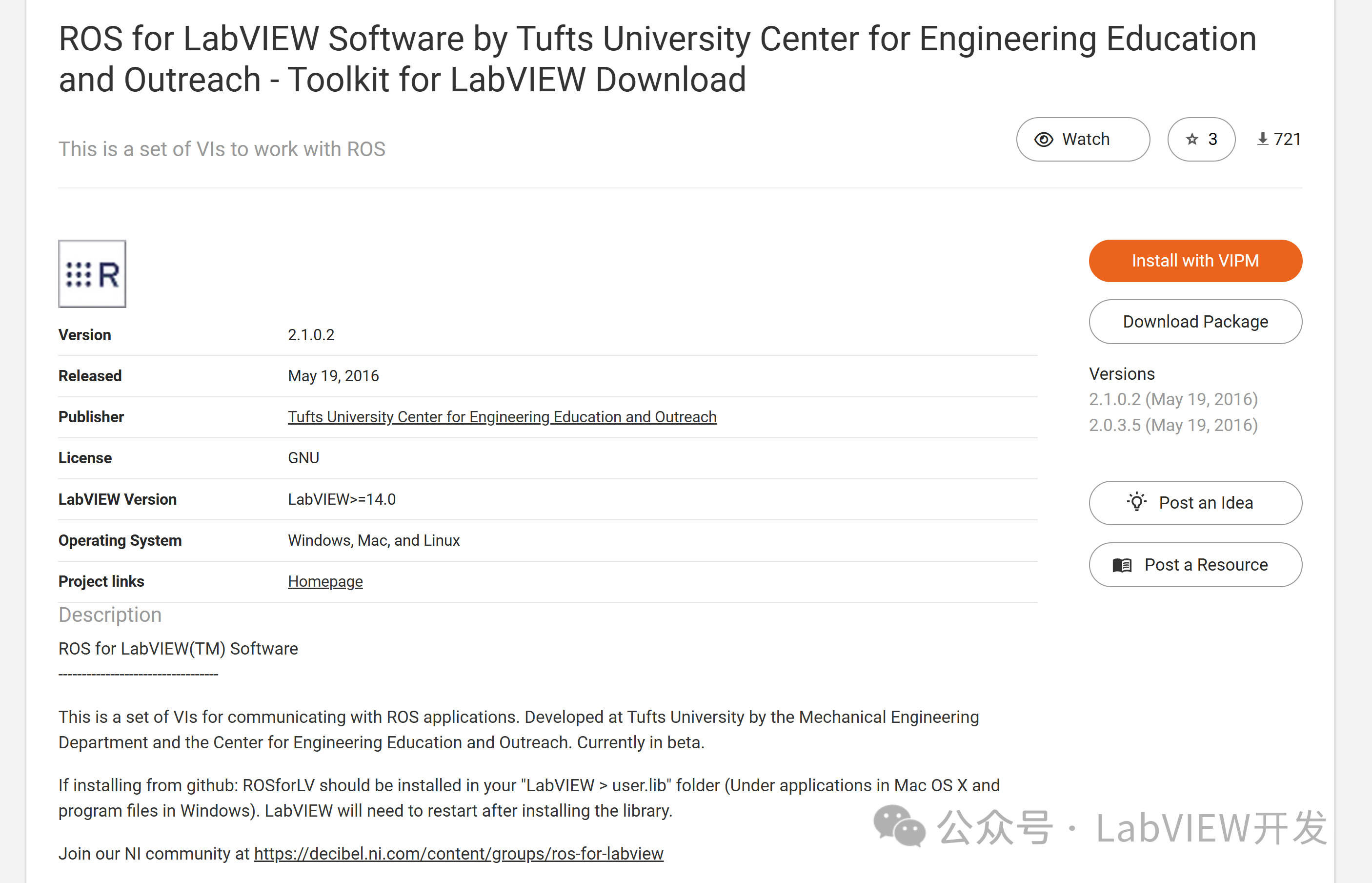
ROS for LabVIEW：实现LabVIEW与ROS的无缝集成
ROS for LabVIEW是由Tufts大学开发的一套VI集合，旨在实现LabVIEW与ROS（Robot Operating System）的无缝集成。ROS是一个灵活的机器人软件框架，而LabVIEW则是一种强大的图形化编程工具。这个工具包的推出使得LabVIEW用户能够直接与R…...
yolov8+ROS+ubuntu18.04——学习记录
参考文献 1.Ubuntu配置Yolov8环境并训练自己的数据集 ROS实时运行 2.https://juejin.cn/post/7313979467965874214 前提： 1.CUDA和Anaconda，PyTorch 2.python>3.8 一、创建激活环境，安装依赖 1.创建虚拟环境 conda create -n yol…...
｜Java中的List与Set转换)
Java小抄(一)｜Java中的List与Set转换
文章目录 List和Set的区别线程安全的区别相互转换List->SetSet->List List和Set的区别 在Java中，List和Set都是集合接口，它们之间有几个关键的区别： 重复元素： List允许重复元素，可以存储相同的元素多次。Set…...
)
【每日随笔】小人畏威不怀德 , 君子畏德不畏威 ( 先礼后兵 )
文章目录 一、小人畏威不怀德1、小人畏威不怀德2、小人场景一3、小人场景二 二、君子畏德不畏威三、先礼后兵 一、小人畏威不怀德 1、小人畏威不怀德 如果 友善 的对待 小人 , 这种人 认知低 且 素质差 , 小人 会将你的 " 友善 " 理解为 " 屈服 " , 他会认…...
不一样的2024
当我们继续往前走时，发现身边的事物不再那么的陌生，也不再那边多的阻碍，不管怎么，2024将会不一样。 当我们走进审批流时，全面石荒芜的，所以自己构建了一个体系。 当我们转向开源时，发现开源与…...
linux mv操作和cp操作
mv 和 cp 是 Linux 系统中用于移动和复制文件或文件夹的两个常用命令，它们之间的主要区别在于： mv（move）：mv 命令用于移动文件或文件夹，将它们从一个位置移动到另一个位置。移动后，原始文件或文…...
web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段： 构建阶段（Build Stage）：…...
vscode里如何用git
打开vs终端执行如下： 1 初始化 Git 仓库（如果尚未初始化） git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框，很难让人不联想到SQL注入，但提示都说了不是SQL注入，所以就不往这方面想了 先查看一下网页源码，发现一段JavaScript代码，有一个关键类ctfs…...
【机器视觉】单目测距——运动结构恢复
ps：图是随便找的，为了凑个封面 前言 在前面对光流法进行进一步改进，希望将2D光流推广至3D场景流时，发现2D转3D过程中存在尺度歧义问题，需要补全摄像头拍摄图像中缺失的深度信息，否则解空间不收敛…...
C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流，定义在 <sstream> 中： std::istringstream：输入流，从已有字符串中读取并解析。std::ostringstream：输出流，向内部缓冲区写入内容，最终取…...
c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署，直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型，但是目前国内可能使用不多，至少实践例子很少看见。开发训练模型就不介绍了&am…...
在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包： for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
Unity | AmplifyShaderEditor插件基础（第七集：平面波动shader）
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件，所以得把软件用docker打包起来，大部分功能都没问题，出了一个奇怪的事情。同样的代码，在本机上用vscode可以运行起来，但是打包之后在docker里出现了问题。使用的是dialog组件，…...
Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral（热门工具 Ruff 的开发者）推出的下一代高性能 Python 包管理器和构建工具，用 Rust 编写。它旨在解决传统工具（如 pip、virtualenv、pip-tools）的性能瓶颈，同时…...