Divisibility Part1(整除理论1)
Divisibility Part1
学习本节的基础:任意个整数之间进行加、减、乘的混合运算之后的结果仍然是整数。之后将不申明地承认这句话的正确性并加以运用。
用一个不为 0 0 0的数去除另一个数所得的商却不一定是整数( a a a除 b b b,写作 b a \frac{b}{a} ab, a a a除以 b b b,写作 a b \frac{a}{b} ba),所以我们需要引进整除的概念,这节会对整除进行深入讨论。
接下来,我们会给出定义,且给出并证明定义引申出的定理,最后对这些加以运用。
定义 1 1 1 设 a , b a,b a,b 是任意两个整数,其中 b ≠ 0 b\neq0 b=0,如果存在一个整数 q q q,使得等式
a = b q ( 1 ) \qquad \qquad \qquad \qquad \qquad a=bq\qquad\qquad\qquad\qquad\qquad(1) a=bq(1)
成立,我们就说 b b b 整除 a a a 或 a a a 被 b b b 整除,记作 b ∣ a b|a b∣a,此时我们把 b b b 叫做 a a a 的因数,把 a a a 叫做 b b b 的倍数。
如果 ( 1 ) (1) (1) 里面的整数 q q q 不存在,我们就说 b b b 不能整除 a a a,记作 b ∤ a b \nmid a b∤a 。
接下来从定义出发,证明一些关于整除的基本定理。
定理 1 1 1(传递性) 若 a a a 是 b b b 的倍数, b b b 是 c c c 的倍数,则 a a a 是 c c c 的倍数,也就是
b ∣ a , c ∣ b ⇒ a ∣ c b|a,c|b \Rarr a|c b∣a,c∣b⇒a∣c
证 由定义 1 1 1,可知 b ∣ a , c ∣ b b|a,c|b b∣a,c∣b,所以存在两个整数 a 1 , b 1 a_1,b_1 a1,b1,使得
a = a 1 b , b = b 1 c a=a_1b,\quad b=b_1c a=a1b,b=b1c
成立,因此
a = ( a 1 b 1 ) c a=(a_1b_1)c a=(a1b1)c
又因为 a 1 , b 1 a_1,b_1 a1,b1 是整数,所以 c ∣ a c|a c∣a。
定理 2 2 2 若 a , b a,b a,b 都是 m m m 的倍数,那么 a ± b a\pm b a±b 也是 m m m 的倍数。
证 a , b a,b a,b 都是 m m m 的倍数,所以存在两个整数 a 1 , b 1 a_1,b_1 a1,b1,使得
a = a 1 m , b = b 1 m a = a_1m,\quad b=b_1m a=a1m,b=b1m
a ± b a\pm b a±b 可以写作
a ± b = ( a 1 ± b 1 ) m a\pm b = (a_1\pm b_1)m a±b=(a1±b1)m
因 a 1 ± b 1 a_1\pm b_1 a1±b1 是整数,故 a ± b a\pm b a±b 是 m m m 的倍数。
同样的方法可以证明
定理 3 3 3 若 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an 都是 m m m 的倍数, q 1 , q 2 , ⋯ , q n q_1,q_2,\cdots,q_n q1,q2,⋯,qn 是任意 n n n 个整数,则 q 1 a 1 + q 2 a 2 + ⋯ + q n a n q_1a_1+q_2a_2+\cdots+q_na_n q1a1+q2a2+⋯+qnan 是 m m m 的倍数。
证 因为 q 1 a 1 , q 2 a 2 , ⋯ , q n a n q_1a_1,q_2a_2,\cdots,q_na_n q1a1,q2a2,⋯,qnan 是 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an 的倍数, a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an 是 m m m 的倍数,由定理 1 1 1 可得 q 1 a 1 , q 2 a 2 , ⋯ , q n a n q_1a_1,q_2a_2,\cdots,q_na_n q1a1,q2a2,⋯,qnan 是 m m m 的倍数
由定理 2 2 2 得 q 1 a 1 + q 2 a 2 + ⋯ + q n a n q_1a_1+q_2a_2+\cdots+q_na_n q1a1+q2a2+⋯+qnan 是 m m m 的倍数。
定理 4 4 4(带余除法) 若 a , b a,b a,b 是任意两个整数,其中 b > 0 b>0 b>0,则存在两个整数 q , r q,r q,r,使得
a = b q + r , 0 ≤ r < b ( 2 ) \qquad \qquad a=bq+r,\quad \: 0\leq r< b \qquad \qquad \qquad \qquad (2) a=bq+r,0≤r<b(2)
成立,而且 q , r q,r q,r 是唯一的。
证 作整数序列
⋯ , − 3 b , − 2 b , − b , 0 , b , 2 b , 3 b , ⋯ \cdots,-3b,-2b,-b,0,b,2b,3b,\cdots ⋯,−3b,−2b,−b,0,b,2b,3b,⋯
那么 a a a 在这个序列的某相邻两项之间,即存在一个整数 q q q,使得
b q ≤ a < b ( q + 1 ) ( 3 ) \qquad \qquad \qquad bq\leq a<b(q+1)\qquad \qquad\qquad\qquad\quad (3) bq≤a<b(q+1)(3)
成立。令 r = a − b q r=a-bq r=a−bq。代入 ( 3 ) (3) (3) 得
0 ≤ r < b 0\leq r<b 0≤r<b
所以存在两个整数 q , r q,r q,r 使得 ( 2 ) (2) (2) 成立。
下面证明 q , r q,r q,r 的唯一性:设 q , r q,r q,r 和 q 1 , r 1 q_1,r_1 q1,r1 是满足 ( 2 ) (2) (2) 的两对整数,则
{ a = b q + r ( 0 ≤ r < b ) a = b q 1 + r 1 ( 0 ≤ r 1 < b ) \begin{cases} a=bq+r\quad(0\leq r<b)\\ a=bq_1+r_1\quad(0\leq r_1<b) \end{cases} {a=bq+r(0≤r<b)a=bq1+r1(0≤r1<b)
联立得
b q + r = b q 1 + r 1 bq+r=bq_1+r_1 bq+r=bq1+r1
移项
b ( q − q 1 ) = r 1 − r b(q-q_1)=r_1-r b(q−q1)=r1−r
由于 r , r 1 r,r_1 r,r1 的值域都是 0 ≤ r < b 0\leq r<b 0≤r<b,所以二者相减的绝对值不超过 b b b。
即
b ∣ q − q 1 ∣ = ∣ r 1 − r ∣ b|q-q_1|=|r_1-r| b∣q−q1∣=∣r1−r∣
解得
{ q = q 1 r = r 1 \begin{cases} q=q_1\\ r=r_1 \end{cases} {q=q1r=r1
证毕。
整数的很多基本性质都可以从定理 ( 4 ) (4) (4) 引导出来,本章最主要的内容都是在定理 ( 4 ) (4) (4) 的基础上建立。
定义 2 2 2 ( 2 ) (2) (2) 中的 q q q 叫做 a a a 被 b b b 除所得到的不完全商, r r r 叫做 a a a 的余数。
习题
一
证明定理 3 3 3。
二
证明 3 ∣ n ( n + 1 ) ( 2 n + 1 ) 3|n(n+1)(2n+1) 3∣n(n+1)(2n+1),其中 n n n 是任意整数。
题解 设 n = 3 γ + r n=3\gamma+r n=3γ+r ( 0 ≤ r < 3 ) (0\leq r<3) (0≤r<3) 得
n ( n + 1 ) ( 2 n + 1 ) = ( 3 γ + r ) ( 3 γ + r + 1 ) ( 6 γ + 2 r + 1 ) n(n+1)(2n+1)=(3\gamma+r)(3\gamma+r+1)(6\gamma+2r+1) n(n+1)(2n+1)=(3γ+r)(3γ+r+1)(6γ+2r+1)
- 当 r = 1 r=1 r=1,那么 2 r + 1 = 3 2r+1=3 2r+1=3 ,又 3 ∣ 6 γ , 3 ∣ 3 3|6\gamma,3|3 3∣6γ,3∣3 所以 3 ∣ ( 6 γ + 2 r + 1 ) 3|(6\gamma+2r+1) 3∣(6γ+2r+1)
所以, 3 ∣ n ( n + 1 ) ( 2 n + 1 ) 3|n(n+1)(2n+1) 3∣n(n+1)(2n+1)。
- 当 r = 2 r=2 r=2,那么 r + 1 = 3 r+1=3 r+1=3,又 3 ∣ 3 γ , 3 ∣ 3 3|3\gamma,3|3 3∣3γ,3∣3 所以 3 ∣ ( 3 γ + r + 1 ) 3|(3\gamma+r+1) 3∣(3γ+r+1)
所以, 3 ∣ n ( n + 1 ) ( 2 n + 1 ) 3|n(n+1)(2n+1) 3∣n(n+1)(2n+1)。
- 当 r = 0 r=0 r=0, 3 ∣ n 3|n 3∣n,所以 3 ∣ n ( n + 1 ) ( n + 1 ) 3|n(n+1)(n+1) 3∣n(n+1)(n+1)。
证毕。
三
若 a x 0 + b y 0 ax_0+by_0 ax0+by0 是形如 a x + b y ax+by ax+by ( ( ( x , y x,y x,y 是任意整数, a , b a,b a,b 是两个不全为零的整数 ) ) ) 的数中最小的正整数,证明
( a x 0 + b y 0 ) ∣ ( a x + b y ) (ax_0+by_0)|(ax+by) (ax0+by0)∣(ax+by)
题解 设
a x + b y = q 1 ( a x 0 + b y 0 ) + r 1 ( 0 ≤ r 1 < a x 0 + b y 0 ) ax+by=q_1(ax_0+by_0)+r_1\quad(0\leq r_1<ax_0+by_0) ax+by=q1(ax0+by0)+r1(0≤r1<ax0+by0)
可得
r 1 = a ( x − q 1 x 0 ) + b ( y − q 1 y 0 ) r_1=a(x-q_1x_0)+b(y-q_1y_0) r1=a(x−q1x0)+b(y−q1y0)
r 1 r_1 r1 满足 a x + b y ax+by ax+by 的形式,而 a x 0 + b y 0 ax_0+by_0 ax0+by0 是形如 a x + b y ax+by ax+by 的数中最小的正整数,设 ( a x 0 + b y 0 ) (ax_0+by_0) (ax0+by0)为 d d d。
所以, r 1 r_1 r1 是 d d d 的倍数,设 r = q 2 d r=q_2d r=q2d,那么 a x + b y = q 1 d + q 2 d ax+by=q_1d+q_2d ax+by=q1d+q2d。
显然 d ∣ ( a x + b y ) d|(ax+by) d∣(ax+by)。
证毕。
四
若 a , b a,b a,b 是任意两个整数,且 b ≠ 0 b\neq0 b=0,证明:存在两个整数 s , t s,t s,t 使得
a = b s + t , ∣ t ∣ ≤ ∣ b ∣ 2 a=bs+t,\quad |t| \leq \frac{|b|}{2} a=bs+t,∣t∣≤2∣b∣
成立,并且当 b b b 是奇数的时候, s , t s,t s,t 是唯一存在的,当 b b b 是偶数的时候,结果如何?
题解 由定理 4 4 4 可知,对任意整数 a , b a,b a,b 都有
a = q b + r , 0 ≤ r < ∣ b ∣ a=qb+r,\quad 0\leq r<|b| a=qb+r,0≤r<∣b∣
- b b b 是正数
若 r ≤ b 2 r\leq\frac{b}{2} r≤2b,则 s = q , t = r s=q,t=r s=q,t=r。
若 r ≥ b 2 r\geq \frac{b}{2} r≥2b ,则 a = ( q + 1 ) b + ( r − b ) a=(q+1)b+(r-b) a=(q+1)b+(r−b),显然 ∣ r − b ∣ < b 2 |r-b|<\frac{b}{2} ∣r−b∣<2b, s = q + 1 , t = r − b s=q+1,t=r-b s=q+1,t=r−b
- b b b 是负数
若 r ≤ ∣ b 2 ∣ r\leq |\frac{b}{2}| r≤∣2b∣,则 s = q , t = r s=q,t=r s=q,t=r。
若 r ≥ ∣ b 2 ∣ r\geq |\frac{b}{2}| r≥∣2b∣,则 a = ( q − 1 ) b + ( r + b ) a=(q-1)b+(r+b) a=(q−1)b+(r+b),显然 ∣ r + b ∣ < b 2 |r+b|<\frac{b}{2} ∣r+b∣<2b, s = q − 1 , t = r + b s=q-1,t=r+b s=q−1,t=r+b
当 b b b 为奇数, b 2 \frac{b}{2} 2b 向下取整,不存在 r = b 2 r=\frac{b}{2} r=2b, s s s 只能取 q q q 或 q − 1 q-1 q−1 或 q + 1 q+1 q+1 中的一个。
当 b b b 为偶数,存在 r = b 2 r=\frac{b}{2} r=2b,所以当 r = b 2 r=\frac{b}{2} r=2b时, s s s 既能取 q q q,又能取 q − 1 q-1 q−1 或 q + 1 q+1 q+1 。
五
检查一个整数 n n n 是否能被 3 3 3 整除。
题解
对于任意一个整数 n n n,都可以写成:
n = a 0 × 1 0 0 + a 1 × 1 0 1 + ⋯ + a n × 1 0 n n=a_0\times10^0+a_1\times 10^1+\dots+a_n\times10^n n=a0×100+a1×101+⋯+an×10n
已知 1 0 i 10^i 10i 除以 3 3 3 的余数是 1 1 1,所以 a i × 1 0 i a_i\times10^i ai×10i 除以 3 3 3 的余数等价于 a i a_i ai 除以 3 3 3 的余数。
那么 n n n 除以 3 3 3 的余数,等价于 ∑ i = 1 n a [ i ] \sum_{i=1}^n a[i] ∑i=1na[i] 除以 3 3 3 的余数。
所以 n n n 能被 3 3 3 整除,等价于 ∑ i = 1 n a [ i ] \sum_{i=1}^{n}a[i] ∑i=1na[i] 能被 3 3 3 整除。
证毕。
六
检查一个整数 n n n 是否能被 4 4 4 整除。
题解
对于任意一个整数 n n n,都可以写成:
n = a 0 × 1 0 0 + a 1 × 1 0 1 + ⋯ + a n × 1 0 n n=a_0\times10^0+a_1\times 10^1+\dots+a_n\times10^n n=a0×100+a1×101+⋯+an×10n
已知 10 10 10 除以 4 4 4 的余数是 2 2 2,已知 1 0 i 10^i 10i ( i ≥ 2 ) (i\geq2) (i≥2)除以 4 4 4 的余数是 0 0 0。
所以 n n n 除以 4 4 4 的余数取决于于 a 0 + a 1 × 1 0 1 a_0+a_1\times10^1 a0+a1×101 除以 4 4 4 的余数。
如果 a 0 + a 1 × 1 0 1 a_0+a_1\times10^1 a0+a1×101 除以 4 4 4 的余数是 0 0 0,那么 n n n 能被 4 4 4 整除
换句话说, n n n 是否能被 4 4 4 整除,取决于 n n n 的最后两位能否被 4 4 4 整除。
证毕。
七
检查一个整数 n n n 是否能被 6 6 6 整除。
题解
先检查最后一位数是否是偶数(是否能被 2 2 2 整除),再利用第五题的结论,检查是否被 3 3 3 整除。
证毕。
八
检查一个整数 n n n 是否能被 7 7 7 整除。
同余做法
等价于直接判断 n m o d 7 n\:mod\:7 nmod7 是否为 0 0 0。
方法是将数字读入到字符串内,然后从最高位开始对 7 7 7 取模然后乘以 10 10 10,再下一位。
最后得到的数为 0 0 0,就说明是 7 7 7 的倍数。
时间复杂度 O ( n ) O(n) O(n) ( n n n 代表数位个数)。
这个方法是通用的,如果时间复杂度允许 7 7 7 可以换成任意的数。
string s;
cin >> s;
int now = 0;
for (int j = 0; j < s.size(); j++) {now = now * 10 + (s[j] - '0');now %= 7;
}
if(now == 0) cout << "Yes" << endl;
else cout << "No" << endl;
相关文章:
)
Divisibility Part1(整除理论1)
Divisibility Part1 学习本节的基础:任意个整数之间进行加、减、乘的混合运算之后的结果仍然是整数。之后将不申明地承认这句话的正确性并加以运用。 用一个不为 0 0 0的数去除另一个数所得的商却不一定是整数( a a a除 b b b,写作 b a \frac…...

代码随想录算法训练营第三十七天 | 860.柠檬水找零、406.根据身高重建队列、452.用最少数量的箭引爆气球
目录 860.柠檬水找零 思路 代码 406.根据身高重建队列 思路 代码 452. 用最少数量的箭引爆气球 思路 代码 860.柠檬水找零 本题看上好像挺难,其实挺简单的,大家先尝试自己做一做。 代码随想录 思路 这题还有什么难不难的,这道题不是非…...

GolangFoundation
GolangFoundation 一. Hello World1.1 SDK1.2 环境1.3 hello world1.4 语法规则二. 程序结构2.1 循环2.2 概述2.3 完整写法2.4 类似while2.5 死循环2.6 特殊循环三. 变量3.1 命名3.2 声明2.3 变量...
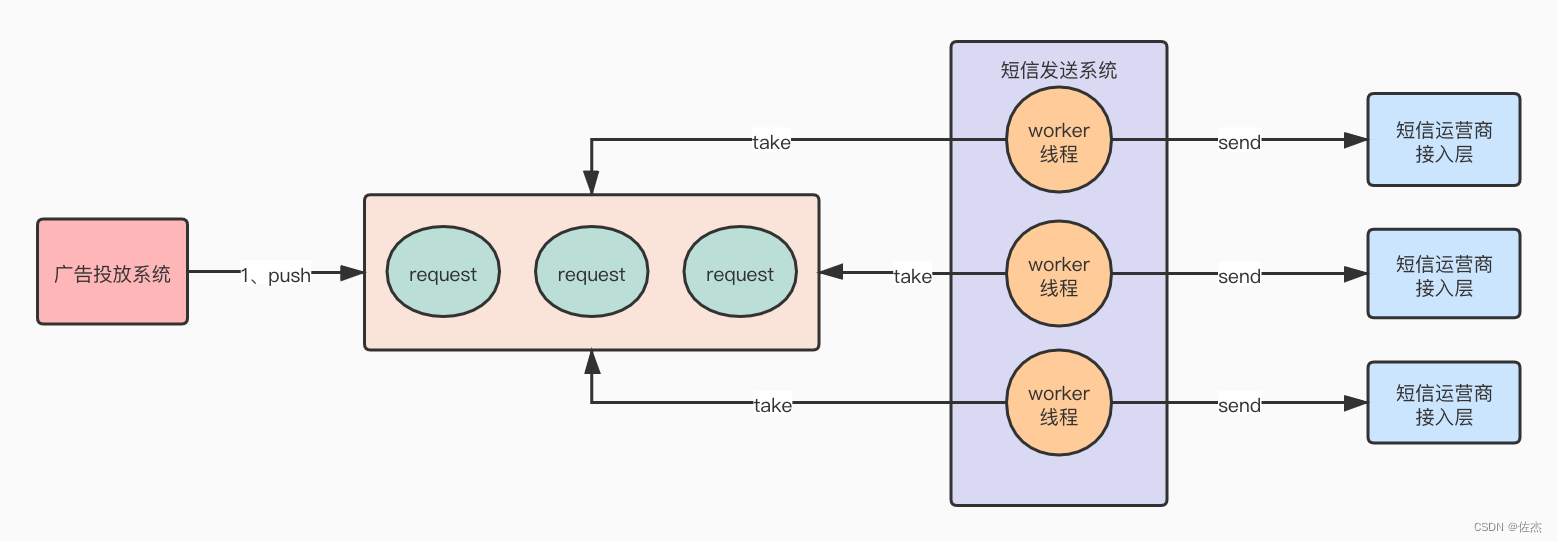
如果任务过多,队列积压怎么处理?
如果任务过多,队列积压怎么处理? 1、内存队列满了应该怎么办2、问题要治本——发短信导致吞吐量降低的问题不能忽略!!3、多路复用IO模型的核心组件简介1、内存队列满了应该怎么办 如图: 大家可以看到,虽然现在发短信和广告投递,彼此之间的执行效率不受彼此影响,但是请…...

FTP协议——BFTPD基本操作(Ubuntu+Win)
1、描述 本机(Win10)与虚拟机(Ubuntu22.04.4)上的BFTPD服务器建立FTP连接,执行一些基本操作。BFTPD安装教程:FTP协议——BFTPD安装(Linux)-CSDN博客 2、 步骤 启动BFTPD。启动文件…...

为什么需要分布式 ID?
目录 为什么需要分布式 ID 分布式 ID 的生成方法 分布式 ID 的应用场景 小结 在现代软件架构中,分布式系统架构变得越来越流行。在这些系统中,由于组件分散在不同的服务器、数据中心甚至不同的地理位置,因此要构建高性能、可扩展的应用系…...

MIT6.828 Lab2-3 Sysinfo
目录 一、实验内容二、实验过程2.1 已有的代码2.2 需补充内容/kernel/kalloc.c修改(剩余内存计算的函数)/kernel/proc.c修改(统计进程数量的函数)/kernel/defs.h修改添加/kernel/sysinfo.c文件/kernel/syscall.h修改/kernel/sysca…...

形态学操作:腐蚀、膨胀、开闭运算、顶帽底帽变换、形态学梯度区别与联系
一、总述相关概念 二、相关问题 1.形态学操作中的腐蚀和膨胀对图像有哪些影响? 形态学操作中的腐蚀和膨胀是两种常见的图像处理技术,它们通过对图像进行局部区域的像素值替换来实现对图像形状的修改。 腐蚀操作通常用于去除图像中的噪声和细小的细节&a…...

StringBufferInputStream类,你学会了吗?
在Java编程中,处理字符串数据流是一项常见的任务。 为了更灵活地处理字符串数据流,Java提供了StringBufferInputStream类,它允许将字符串转换为输入流,从而可以像处理其他输入流一样对字符串进行操作。 本文将深入探讨StringBufferInputStream类的背景、用法、优缺点以及…...
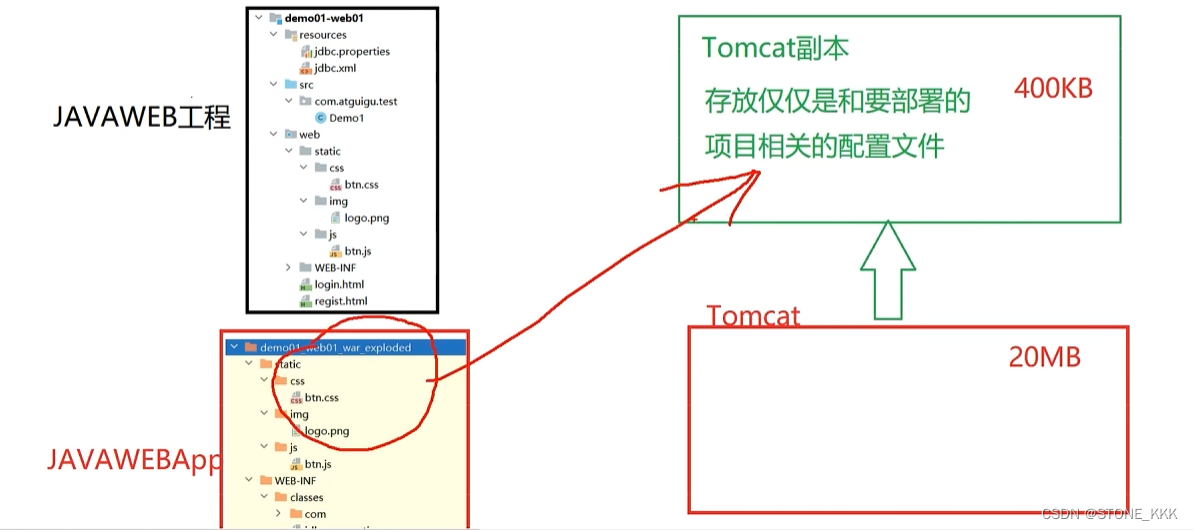
06_Tomcat
文章目录 Tomcat1.概念2.Tomcat安装3.Tomcat项目结构4.标准web项目结构5.Tomcat部署项目方式6.IDEA关联Tomcat6.1 构建tomcat和idea关联6.2 使用idea创建一个Javaweb工程6.3 使用idea将工程**构建**成一个app6.4 使用idea将构建好的app**部署**到tomcat中 Tomcat 1.概念 Tomc…...
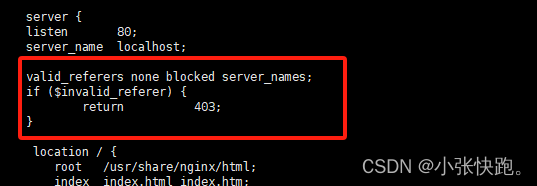
系统安全扫描扫出了:可能存在 CSRF 攻击怎么办
公司的H5在软件安全测试中被检查出可能存在 CSRF 攻击,网上找了一堆解决方法,最后用这种方式解决了。 1、问题描述 CSRF 是 Cross Site Request Forgery的缩写(也缩写为也就是在用户会话下对某个 CGI 做一些 GET/POST 的事,RIVTSTCNNARGO一这…...
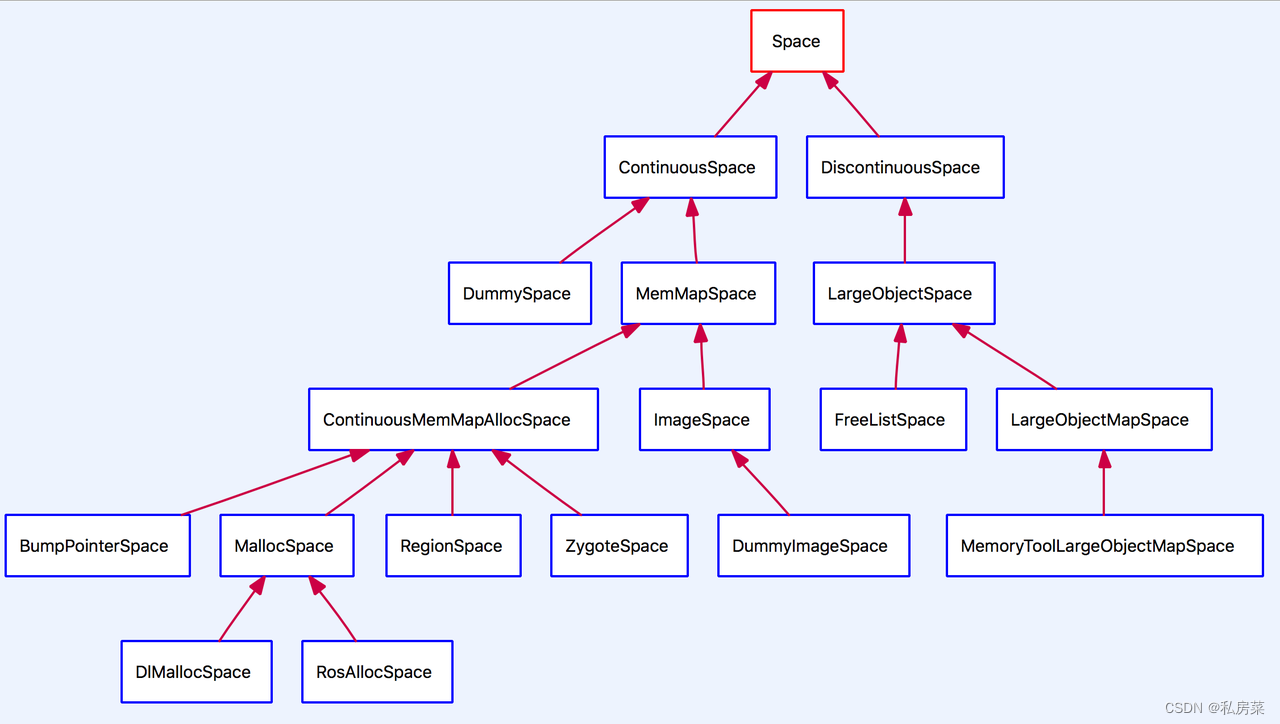
Android ART 虚拟机简析
源码基于:Android U 1. prop 名称选项名称heap 变量名称功能 dalvik.vm.heapstartsize MemoryInitialSize initial_heap_size_ 虚拟机在启动时,向系统申请的起始内存 dalvik.vm.heapgrowthlimit HeapGrowthLimit growth_limit_ 应用可使用的 max…...
Android低代码开发 - MenuPanel的源码剖析和基本使用
看了我上篇文章Android低代码开发 - 像启蒙和乐高玩具一样的MenuPanel 之后,本篇开始讲解代码。 源代码剖析 首先从MenuPanelItemRoot讲起。 package dora.widget.panelinterface MenuPanelItemRoot {/*** 菜单的标题。** return*/var title: String?fun hasTit…...

Leetcode刷题笔记3
18. 四数之和 18. 四数之和 - 力扣(LeetCode) 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应&…...
初识C语言——第二十九天
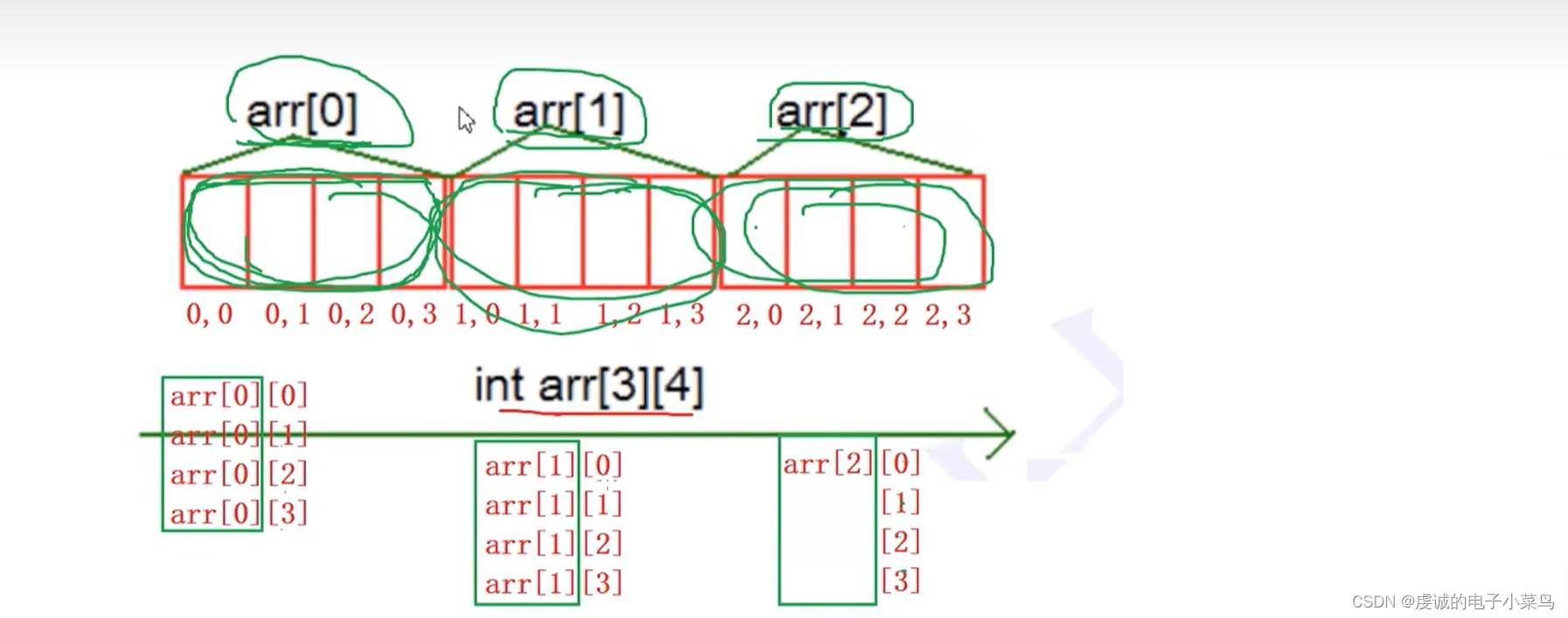
数组 本章重点 1.一维数组的创建和初始化 数组的创建 注意事项: 1.一维由低数组在内存中是连续存放的! 2.随着数组下标的增长,地址是由低到高变化的 2.二维数组的创建和初始化 注意事项: 1.二维数组在内存中也是连续存放的&am…...

LeetCode27.移除元素
题目链接: 27. 移除元素 - 力扣(LeetCode) 思路分析:同样属于经典的双指针移动问题,要掌握固定的思路即可。 算法分析:这个题目可以这样处理,我们把所有非val 的元素都向前移动,把…...

DiffMap:首个利用LDM来增强高精地图构建的网络
论文标题: DiffMap: Enhancing Map Segmentation with Map Prior Using Diffusion Model 论文作者: Peijin Jia, Tuopu Wen, Ziang Luo, Mengmeng Yang, Kun Jiang, Zhiquan Lei, Xuewei Tang, Ziyuan Liu, Le Cui, Kehua Sheng, Bo Zhang, Diange Ya…...

ComfyUI简单介绍
🍓什么是ComfyUI ComfyUI是一个为Stable Diffusion专门设计的基于节点的图形用户界面,可以通过各种不同的节点快速搭建自己的绘图工作流程。 软件打开之后是长这个样子: 同时软件本身是github上的一个开源项目,开源地址为&#…...

【内存泄漏Bug】animation未释放
问题描述 一个页面做了动画特效,这个页面有可能跳转到其他页面,并长时间不返回,该页面此时已经不活跃了,该页面的对象为无用对象,存在内存泄漏风险 问题分析 这个activity的特性是 1. 有可能跳转到其他页面 2. 有可…...

《异常检测——从经典算法到深度学习》28 UNRAVEL ANOMALIES:基于周期与趋势分解的时间序列异常检测端到端方法
《异常检测——从经典算法到深度学习》 0 概论1 基于隔离森林的异常检测算法 2 基于LOF的异常检测算法3 基于One-Class SVM的异常检测算法4 基于高斯概率密度异常检测算法5 Opprentice——异常检测经典算法最终篇6 基于重构概率的 VAE 异常检测7 基于条件VAE异常检测8 Donut: …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
