Habicht定理中有关子结式命题3.4.6的证明


个人认为红色区域有问题,因为 deg ( ϕ ( S j ) ) = r \deg{\left( \phi\left( S_{j} \right) \right) = r} deg(ϕ(Sj))=r,当 i ≥ r i \geq r i≥r时, s u b r e s i ( ϕ ( S j + 1 ) , ϕ ( S j ) ) subres_{i}\left( \phi(S_{j + 1}),\phi\left( S_{j} \right) \right) subresi(ϕ(Sj+1),ϕ(Sj))的定义不存在!!!
下面是我的证明过程:
【证明】
(a)
因为 ϕ ( R j + 1 2 ( j − i ) S i ) = ϕ ( s u b r e s i ( S j + 1 , S j ) ) = d e t p o l ( x j − i − 1 ϕ ( S j + 1 ) , … , ϕ ( S j + 1 ) , x j − i ϕ ( S j ) , … , ϕ ( S j ) ) {\phi\left( R_{j + 1}^{2(j - i)}S_{i} \right) }{= \phi\left( subres_{i}\left( S_{j + 1},S_{j} \right) \right) }{= detpol\left( x^{j - i - 1}\phi\left( S_{j + 1} \right),\ldots,\phi\left( S_{j + 1} \right),x^{j - i}\phi\left( S_{j} \right),\ldots,\phi\left( S_{j} \right) \right)} ϕ(Rj+12(j−i)Si)=ϕ(subresi(Sj+1,Sj))=detpol(xj−i−1ϕ(Sj+1),…,ϕ(Sj+1),xj−iϕ(Sj),…,ϕ(Sj))
而当 r + 1 ≤ i ≤ j − 1 r + 1 \leq i \leq j - 1 r+1≤i≤j−1时,有
deg ( ϕ ( S j + 1 ) ) = j + 1 > deg ( x j − i ϕ ( S j ) ) + 1 = j − ( r + 1 ) + r + 1 = j \deg\left( \phi\left( S_{j + 1} \right) \right) = j + 1 > \deg\left( x^{j - i}\phi\left( S_{j} \right) \right) + 1 = j - (r + 1) + r + 1 = j deg(ϕ(Sj+1))=j+1>deg(xj−iϕ(Sj))+1=j−(r+1)+r+1=j
此时有 d e t p o l ( x j − i − 1 ϕ ( S j + 1 ) , … , ϕ ( S j + 1 ) , x j − i ϕ ( S j ) , … , ϕ ( S j ) ) = 0 detpol\left( x^{j - i - 1}\phi\left( S_{j + 1} \right),\ldots,\phi\left( S_{j + 1} \right),x^{j - i}\phi\left( S_{j} \right),\ldots,\phi\left( S_{j} \right) \right) = 0 detpol(xj−i−1ϕ(Sj+1),…,ϕ(Sj+1),xj−iϕ(Sj),…,ϕ(Sj))=0,也就是 ϕ ( R j + 1 2 ( j − i ) S i ) = 0 \phi\left( R_{j + 1}^{2(j - i)}S_{i} \right) = 0 ϕ(Rj+12(j−i)Si)=0,即 ϕ ( S j − 1 ) = ϕ ( S j − 2 ) = … = ϕ ( S r + 1 ) = 0 \phi\left( S_{j - 1} \right) = \phi\left( S_{j - 2} \right) = \ldots = \phi\left( S_{r + 1} \right) = 0 ϕ(Sj−1)=ϕ(Sj−2)=…=ϕ(Sr+1)=0。
(b)
- 若 j = n j = n j=n,有
ϕ ( S r ) = d e t p o l ( x n − r − 1 ϕ ( S n + 1 ) , … , ϕ ( S n + 1 ) , x n − r ϕ ( S n ) , … , ϕ ( S n ) ) \phi\left( S_{r} \right) = detpol\left( x^{n - r - 1}\phi\left( S_{n + 1} \right),\ldots,\phi\left( S_{n + 1} \right),x^{n - r}\phi\left( S_{n} \right),\ldots,\phi\left( S_{n} \right) \right) ϕ(Sr)=detpol(xn−r−1ϕ(Sn+1),…,ϕ(Sn+1),xn−rϕ(Sn),…,ϕ(Sn))
由于 deg ( ϕ ( S n + 1 ) ) = n + 1 = deg ( x n − r ϕ ( S n ) ) + 1 = n − r + r + 1 = n + 1 \deg{\left( \phi\left( S_{n + 1} \right) \right) = n + 1 = \deg\left( x^{n - r}\phi\left( S_{n} \right) \right) + 1 = n - r + r + 1 = n + 1} deg(ϕ(Sn+1))=n+1=deg(xn−rϕ(Sn))+1=n−r+r+1=n+1,所以
ϕ ( S r ) = [ l c ( ϕ ( S n + 1 ) , x ) l c ( ϕ ( S n ) , x ) ] n − r ϕ ( S n ) \phi\left( S_{r} \right) = \left\lbrack lc\left( \phi\left( S_{n + 1} \right),x \right)lc\left( \phi\left( S_{n} \right),x \right) \right\rbrack^{n - r}\phi\left( S_{n} \right) ϕ(Sr)=[lc(ϕ(Sn+1),x)lc(ϕ(Sn),x)]n−rϕ(Sn)
- 若 j < n j < n j<n,则
ϕ ( R j + 1 2 ( j − r ) S r ) = d e t p o l ( x j − r − 1 ϕ ( S j + 1 ) , … , ϕ ( S j + 1 ) , x j − r ϕ ( S j ) , … , ϕ ( S j ) ) \phi\left( R_{j + 1}^{2(j - r)}S_{r} \right) = detpol\left( x^{j - r - 1}\phi\left( S_{j + 1} \right),\ldots,\phi\left( S_{j + 1} \right),x^{j - r}\phi\left( S_{j} \right),\ldots,\phi\left( S_{j} \right) \right) ϕ(Rj+12(j−r)Sr)=detpol(xj−r−1ϕ(Sj+1),…,ϕ(Sj+1),xj−rϕ(Sj),…,ϕ(Sj))
由于
deg ( ϕ ( S j + 1 ) ) = j + 1 = deg ( x j − r ϕ ( S n ) ) + 1 = j − r + r + 1 = j + 1 \deg{\left( \phi\left( S_{j + 1} \right) \right) = j + 1 = \deg\left( x^{j - r}\phi\left( S_{n} \right) \right) + 1 = j - r + r + 1 = j + 1} deg(ϕ(Sj+1))=j+1=deg(xj−rϕ(Sn))+1=j−r+r+1=j+1
所以
ϕ ( R j + 1 2 ( j − r ) S r ) = [ ϕ ( R j + 1 ) l c ( ϕ ( S n ) , x ) ] j − r ϕ ( S j ) \phi\left( R_{j + 1}^{2(j - r)}S_{r} \right) = \left\lbrack \phi\left( R_{j + 1} \right)lc\left( \phi\left( S_{n} \right),x \right) \right\rbrack^{j - r}\phi\left( S_{j} \right) ϕ(Rj+12(j−r)Sr)=[ϕ(Rj+1)lc(ϕ(Sn),x)]j−rϕ(Sj)
即
ϕ ( R j + 1 j − r S r ) = l c ( ϕ ( S n ) , x ) j − r ϕ ( S j ) \phi\left( R_{j + 1}^{j - r}S_{r} \right) = {lc\left( \phi\left( S_{n} \right),x \right)}^{j - r}\phi\left( S_{j} \right)\ ϕ(Rj+1j−rSr)=lc(ϕ(Sn),x)j−rϕ(Sj)
(c)
- 若 j = n j = n j=n,有
ϕ ( S r − 1 ) = d e t p o l ( x n − r ϕ ( S n + 1 ) , … , ϕ ( S n + 1 ) , x n − r + 1 ϕ ( S n ) , … , x ϕ ( S n ) , ϕ ( S n ) ) = ( − 1 ) n − r + 2 d e t p o l ( x n − r ϕ ( S n + 1 ) , … , x ϕ ( S n + 1 ) , x n − r + 1 ϕ ( S n ) , … , x ϕ ( S n ) , ϕ ( S n ) , ϕ ( S n + 1 ) ) {\phi\left( S_{r - 1} \right) = detpol\left( x^{n - r}\phi\left( S_{n + 1} \right),\ldots,\phi\left( S_{n + 1} \right),x^{n - r + 1}\phi\left( S_{n} \right),\ldots,x\phi\left( S_{n} \right),\phi\left( S_{n} \right) \right) }{= ( - 1)^{n - r + 2}detpol\left( x^{n - r}\phi\left( S_{n + 1} \right),\ldots,x\phi\left( S_{n + 1} \right),x^{n - r + 1}\phi\left( S_{n} \right),\ldots,x\phi\left( S_{n} \right),\phi\left( S_{n} \right),\phi\left( S_{n + 1} \right) \right)} ϕ(Sr−1)=detpol(xn−rϕ(Sn+1),…,ϕ(Sn+1),xn−r+1ϕ(Sn),…,xϕ(Sn),ϕ(Sn))=(−1)n−r+2detpol(xn−rϕ(Sn+1),…,xϕ(Sn+1),xn−r+1ϕ(Sn),…,xϕ(Sn),ϕ(Sn),ϕ(Sn+1))
由于
deg ( x ϕ ( S n + 1 ) ) = n + 2 = deg ( x n − r + 1 ϕ ( S n ) ) + 1 = n − r + 1 + r + 1 = n + 2 \deg{\left( x\phi\left( S_{n + 1} \right) \right) = n + 2 = \deg\left( x^{n - r + 1}\phi\left( S_{n} \right) \right) + 1 = n - r + 1 + r + 1 = n + 2} deg(xϕ(Sn+1))=n+2=deg(xn−r+1ϕ(Sn))+1=n−r+1+r+1=n+2,
deg ( ϕ ( S n + 1 ) ) = n + 1 = deg ( x n − r + 1 ϕ ( S n ) ) \deg{\left( \phi\left( S_{n + 1} \right) \right) = n + 1 = \deg\left( x^{n - r + 1}\phi\left( S_{n} \right) \right)} deg(ϕ(Sn+1))=n+1=deg(xn−r+1ϕ(Sn))
所以
ϕ ( S r − 1 ) = [ − l c ( ϕ ( S n + 1 ) , x ) ] n − r d e t p o l ( x n − r + 1 ϕ ( S n ) , … , x ϕ ( S n ) , ϕ ( S n ) , ϕ ( S n + 1 ) ) = [ − l c ( ϕ ( S n + 1 ) , x ) ] n − r p r e m ( ϕ ( S n + 1 ) , ϕ ( S n ) , x ) \phi\left( S_{r - 1} \right) = \left\lbrack - lc\left( \phi\left( S_{n + 1} \right),x \right) \right\rbrack^{n - r}detpol\left( x^{n - r + 1}\phi\left( S_{n} \right),\ldots,x\phi\left( S_{n} \right),\phi\left( S_{n} \right),\phi\left( S_{n + 1} \right) \right) = \left\lbrack - lc\left( \phi\left( S_{n + 1} \right),x \right) \right\rbrack^{n - r}prem\left( \phi\left( S_{n + 1} \right),\phi\left( S_{n} \right),x \right) ϕ(Sr−1)=[−lc(ϕ(Sn+1),x)]n−rdetpol(xn−r+1ϕ(Sn),…,xϕ(Sn),ϕ(Sn),ϕ(Sn+1))=[−lc(ϕ(Sn+1),x)]n−rprem(ϕ(Sn+1),ϕ(Sn),x)
- 若 j < n j < n j<n,有
ϕ ( R j + 1 2 ( j − r + 1 ) S r − 1 ) = d e t p o l ( x j − r ϕ ( S j + 1 ) , … , ϕ ( S j + 1 ) , x j − r + 1 ϕ ( S j ) , … , x ϕ ( S j ) , ϕ ( S j ) ) = ( − 1 ) j − r + 2 d e t p o l ( x j − r ϕ ( S j + 1 ) , … , x ϕ ( S j + 1 ) , x j − r + 1 ϕ ( S j ) , … , x ϕ ( S j ) , ϕ ( S j ) , ϕ ( S j + 1 ) ) {\phi\left( R_{j + 1}^{2(j - r + 1)}S_{r - 1} \right) = detpol\left( x^{j - r}\phi\left( S_{j + 1} \right),\ldots,\phi\left( S_{j + 1} \right),x^{j - r + 1}\phi\left( S_{j} \right),\ldots,x\phi\left( S_{j} \right),\phi\left( S_{j} \right) \right) }{= ( - 1)^{j - r + 2}detpol\left( x^{j - r}\phi\left( S_{j + 1} \right),\ldots,x\phi\left( S_{j + 1} \right),x^{j - r + 1}\phi\left( S_{j} \right),\ldots,x\phi\left( S_{j} \right),\phi\left( S_{j} \right),\phi\left( S_{j + 1} \right) \right)} ϕ(Rj+12(j−r+1)Sr−1)=detpol(xj−rϕ(Sj+1),…,ϕ(Sj+1),xj−r+1ϕ(Sj),…,xϕ(Sj),ϕ(Sj))=(−1)j−r+2detpol(xj−rϕ(Sj+1),…,xϕ(Sj+1),xj−r+1ϕ(Sj),…,xϕ(Sj),ϕ(Sj),ϕ(Sj+1))
由于
deg ( x ϕ ( S j + 1 ) ) = j + 2 = deg ( x j − r + 1 ϕ ( S n ) ) + 1 = j − r + r + 1 + 1 = j + 2 = deg ( ( S j + 1 ) ) + 1 = j + 1 + 1 = j + 2 {\deg\left( x\phi\left( S_{j + 1} \right) \right) = j + 2 }{= \deg\left( x^{j - r + 1}\phi\left( S_{n} \right) \right) + 1 = j - r + r + 1 + 1 = j + 2 }{= \deg{\left( \left( S_{j + 1} \right) \right) + 1} = j + 1 + 1 = j + 2} deg(xϕ(Sj+1))=j+2=deg(xj−r+1ϕ(Sn))+1=j−r+r+1+1=j+2=deg((Sj+1))+1=j+1+1=j+2
所以
ϕ ( R j + 1 2 ( j − r + 1 ) S r − 1 ) = ( − 1 ) j − r + 2 [ ϕ ( R j + 1 ) ] j − r d e t p o l ( x j − r + 1 ϕ ( S j ) , … , x ϕ ( S j ) , ϕ ( S j ) , ϕ ( S j + 1 ) ) {\phi\left( R_{j + 1}^{2(j - r + 1)}S_{r-1} \right) }{= ( - 1)^{j - r + 2}\left\lbrack \phi\left( R_{j + 1} \right) \right\rbrack^{j - r}detpol\left( x^{j - r + 1}\phi\left( S_{j} \right),\ldots,x\phi\left( S_{j} \right),\phi\left( S_{j} \right),\phi\left( S_{j + 1} \right) \right) } ϕ(Rj+12(j−r+1)Sr−1)=(−1)j−r+2[ϕ(Rj+1)]j−rdetpol(xj−r+1ϕ(Sj),…,xϕ(Sj),ϕ(Sj),ϕ(Sj+1))
即
ϕ ( − R j + 1 j − r + 2 ) ϕ ( S r − 1 ) = p r e m ( ϕ ( S j ) , ϕ ( S j + 1 ) ) \phi\left( - R_{j + 1}^{j - r + 2} \right)\phi\left( S_{r-1} \right) = prem\left( \phi\left( S_{j} \right),\phi\left( S_{j + 1} \right) \right) ϕ(−Rj+1j−r+2)ϕ(Sr−1)=prem(ϕ(Sj),ϕ(Sj+1))
相关文章:

Habicht定理中有关子结式命题3.4.6的证明
个人认为红色区域有问题,因为 deg ( ϕ ( S j ) ) r \deg{\left( \phi\left( S_{j} \right) \right) r} deg(ϕ(Sj))r,当 i ≥ r i \geq r i≥r时, s u b r e s i ( ϕ ( S j 1 ) , ϕ ( S j ) ) subres_{i}\left( \phi(S_{j 1}),\p…...

【Unity AR开发插件】如何快速地开发可热更的AR应用
预告 本专栏将介绍如何使用这个支持热更的AR开发插件,快速地开发AR应用。 Unity AR开发插件使用教程 更新 二、使用插件一键安装HybridCLR和ARCore 三、配置带HybridCLR的ARCore开发环境 四、制作热更数据-AR图片识别场景...
)
Divisibility Part1(整除理论1)
Divisibility Part1 学习本节的基础:任意个整数之间进行加、减、乘的混合运算之后的结果仍然是整数。之后将不申明地承认这句话的正确性并加以运用。 用一个不为 0 0 0的数去除另一个数所得的商却不一定是整数( a a a除 b b b,写作 b a \frac…...

代码随想录算法训练营第三十七天 | 860.柠檬水找零、406.根据身高重建队列、452.用最少数量的箭引爆气球
目录 860.柠檬水找零 思路 代码 406.根据身高重建队列 思路 代码 452. 用最少数量的箭引爆气球 思路 代码 860.柠檬水找零 本题看上好像挺难,其实挺简单的,大家先尝试自己做一做。 代码随想录 思路 这题还有什么难不难的,这道题不是非…...

GolangFoundation
GolangFoundation 一. Hello World1.1 SDK1.2 环境1.3 hello world1.4 语法规则二. 程序结构2.1 循环2.2 概述2.3 完整写法2.4 类似while2.5 死循环2.6 特殊循环三. 变量3.1 命名3.2 声明2.3 变量...
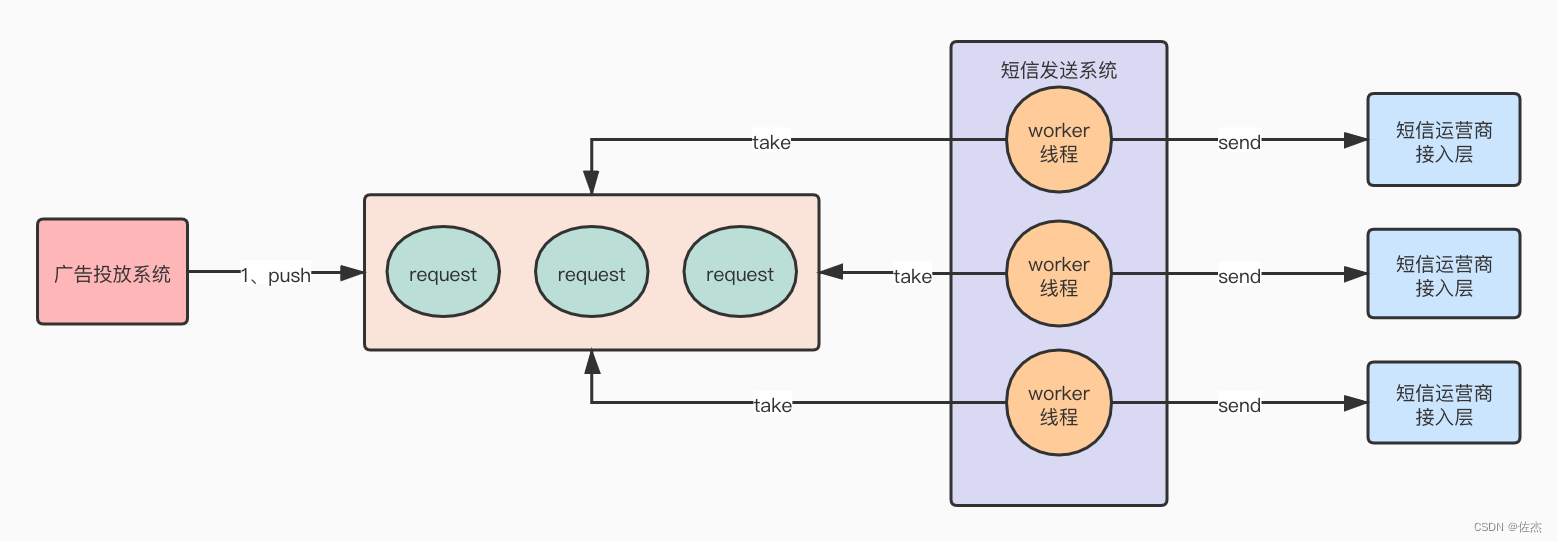
如果任务过多,队列积压怎么处理?
如果任务过多,队列积压怎么处理? 1、内存队列满了应该怎么办2、问题要治本——发短信导致吞吐量降低的问题不能忽略!!3、多路复用IO模型的核心组件简介1、内存队列满了应该怎么办 如图: 大家可以看到,虽然现在发短信和广告投递,彼此之间的执行效率不受彼此影响,但是请…...

FTP协议——BFTPD基本操作(Ubuntu+Win)
1、描述 本机(Win10)与虚拟机(Ubuntu22.04.4)上的BFTPD服务器建立FTP连接,执行一些基本操作。BFTPD安装教程:FTP协议——BFTPD安装(Linux)-CSDN博客 2、 步骤 启动BFTPD。启动文件…...

为什么需要分布式 ID?
目录 为什么需要分布式 ID 分布式 ID 的生成方法 分布式 ID 的应用场景 小结 在现代软件架构中,分布式系统架构变得越来越流行。在这些系统中,由于组件分散在不同的服务器、数据中心甚至不同的地理位置,因此要构建高性能、可扩展的应用系…...

MIT6.828 Lab2-3 Sysinfo
目录 一、实验内容二、实验过程2.1 已有的代码2.2 需补充内容/kernel/kalloc.c修改(剩余内存计算的函数)/kernel/proc.c修改(统计进程数量的函数)/kernel/defs.h修改添加/kernel/sysinfo.c文件/kernel/syscall.h修改/kernel/sysca…...

形态学操作:腐蚀、膨胀、开闭运算、顶帽底帽变换、形态学梯度区别与联系
一、总述相关概念 二、相关问题 1.形态学操作中的腐蚀和膨胀对图像有哪些影响? 形态学操作中的腐蚀和膨胀是两种常见的图像处理技术,它们通过对图像进行局部区域的像素值替换来实现对图像形状的修改。 腐蚀操作通常用于去除图像中的噪声和细小的细节&a…...

StringBufferInputStream类,你学会了吗?
在Java编程中,处理字符串数据流是一项常见的任务。 为了更灵活地处理字符串数据流,Java提供了StringBufferInputStream类,它允许将字符串转换为输入流,从而可以像处理其他输入流一样对字符串进行操作。 本文将深入探讨StringBufferInputStream类的背景、用法、优缺点以及…...
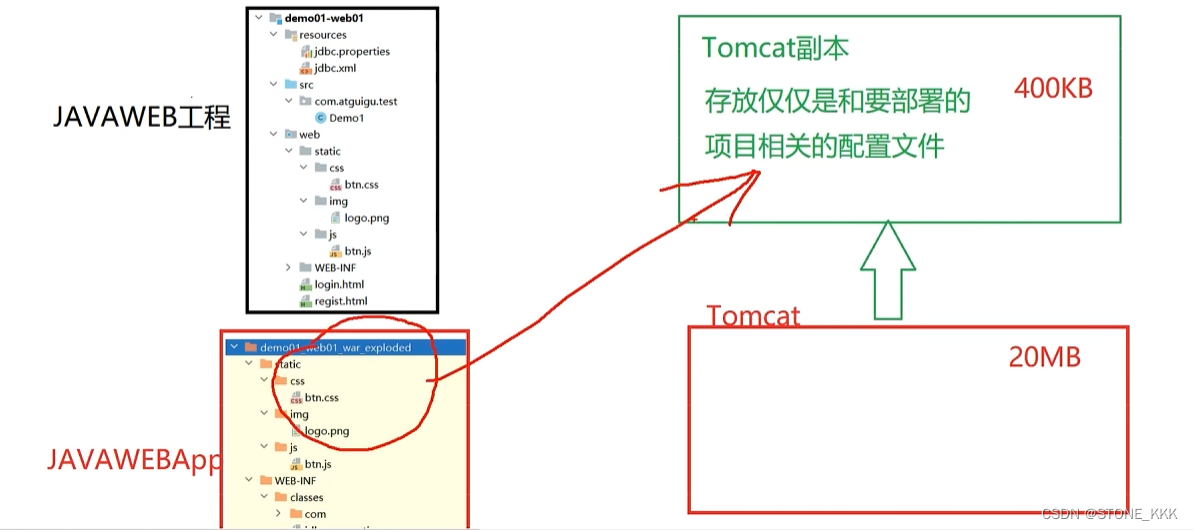
06_Tomcat
文章目录 Tomcat1.概念2.Tomcat安装3.Tomcat项目结构4.标准web项目结构5.Tomcat部署项目方式6.IDEA关联Tomcat6.1 构建tomcat和idea关联6.2 使用idea创建一个Javaweb工程6.3 使用idea将工程**构建**成一个app6.4 使用idea将构建好的app**部署**到tomcat中 Tomcat 1.概念 Tomc…...
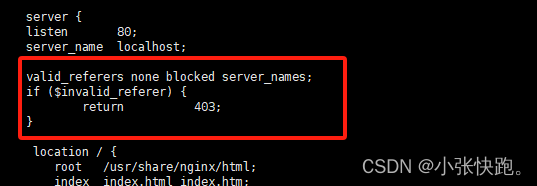
系统安全扫描扫出了:可能存在 CSRF 攻击怎么办
公司的H5在软件安全测试中被检查出可能存在 CSRF 攻击,网上找了一堆解决方法,最后用这种方式解决了。 1、问题描述 CSRF 是 Cross Site Request Forgery的缩写(也缩写为也就是在用户会话下对某个 CGI 做一些 GET/POST 的事,RIVTSTCNNARGO一这…...
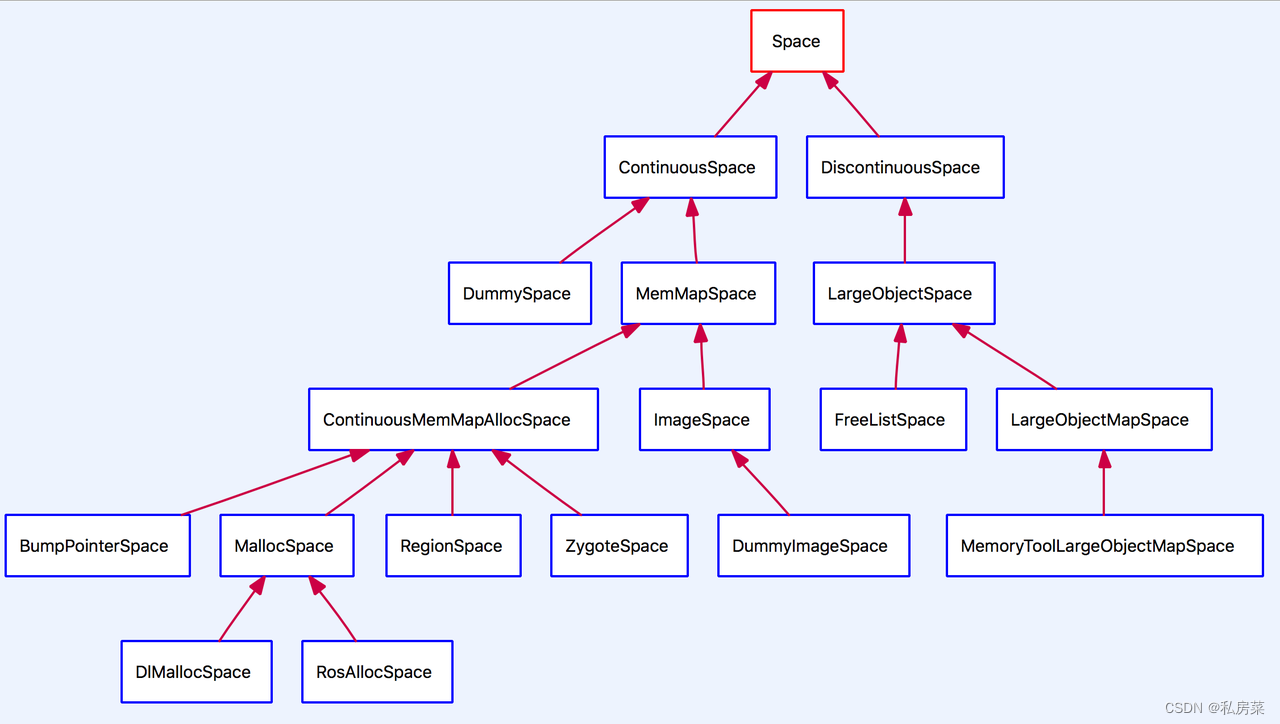
Android ART 虚拟机简析
源码基于:Android U 1. prop 名称选项名称heap 变量名称功能 dalvik.vm.heapstartsize MemoryInitialSize initial_heap_size_ 虚拟机在启动时,向系统申请的起始内存 dalvik.vm.heapgrowthlimit HeapGrowthLimit growth_limit_ 应用可使用的 max…...
Android低代码开发 - MenuPanel的源码剖析和基本使用
看了我上篇文章Android低代码开发 - 像启蒙和乐高玩具一样的MenuPanel 之后,本篇开始讲解代码。 源代码剖析 首先从MenuPanelItemRoot讲起。 package dora.widget.panelinterface MenuPanelItemRoot {/*** 菜单的标题。** return*/var title: String?fun hasTit…...

Leetcode刷题笔记3
18. 四数之和 18. 四数之和 - 力扣(LeetCode) 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应&…...
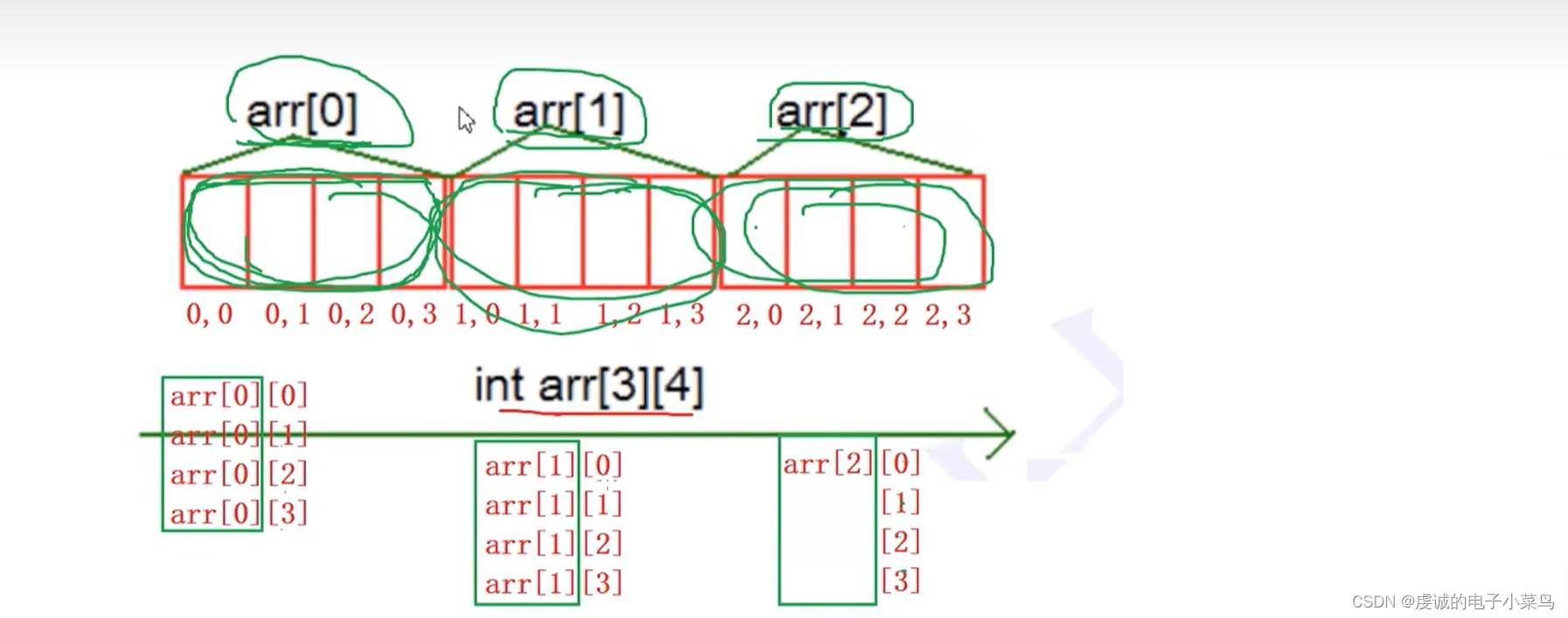
初识C语言——第二十九天
数组 本章重点 1.一维数组的创建和初始化 数组的创建 注意事项: 1.一维由低数组在内存中是连续存放的! 2.随着数组下标的增长,地址是由低到高变化的 2.二维数组的创建和初始化 注意事项: 1.二维数组在内存中也是连续存放的&am…...

LeetCode27.移除元素
题目链接: 27. 移除元素 - 力扣(LeetCode) 思路分析:同样属于经典的双指针移动问题,要掌握固定的思路即可。 算法分析:这个题目可以这样处理,我们把所有非val 的元素都向前移动,把…...

DiffMap:首个利用LDM来增强高精地图构建的网络
论文标题: DiffMap: Enhancing Map Segmentation with Map Prior Using Diffusion Model 论文作者: Peijin Jia, Tuopu Wen, Ziang Luo, Mengmeng Yang, Kun Jiang, Zhiquan Lei, Xuewei Tang, Ziyuan Liu, Le Cui, Kehua Sheng, Bo Zhang, Diange Ya…...

ComfyUI简单介绍
🍓什么是ComfyUI ComfyUI是一个为Stable Diffusion专门设计的基于节点的图形用户界面,可以通过各种不同的节点快速搭建自己的绘图工作流程。 软件打开之后是长这个样子: 同时软件本身是github上的一个开源项目,开源地址为&#…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
