小米8SE刷root(面具)
首先准备好一根数据线,一部小米8SE手机,和一台电脑
接下来需要的软件我会给出链接和使用方法,以及分享我遇到的困难和解决方案
下面操作不会的,可以参考这个博主的教程,我也是跟着这个教程刷好的
第一步解锁BL
开启开发者模式:打开设置->我的设备->全部参数->MIUI版本连续点击七次开启开发者模式
申请解锁BL:打开设置->更多设置->开发者选项(OEM解锁)->设备解锁状态->绑定账号和设备
开始解锁BL:先访问设备解锁状态中提供的网站,根据提示下载软件并进行解锁
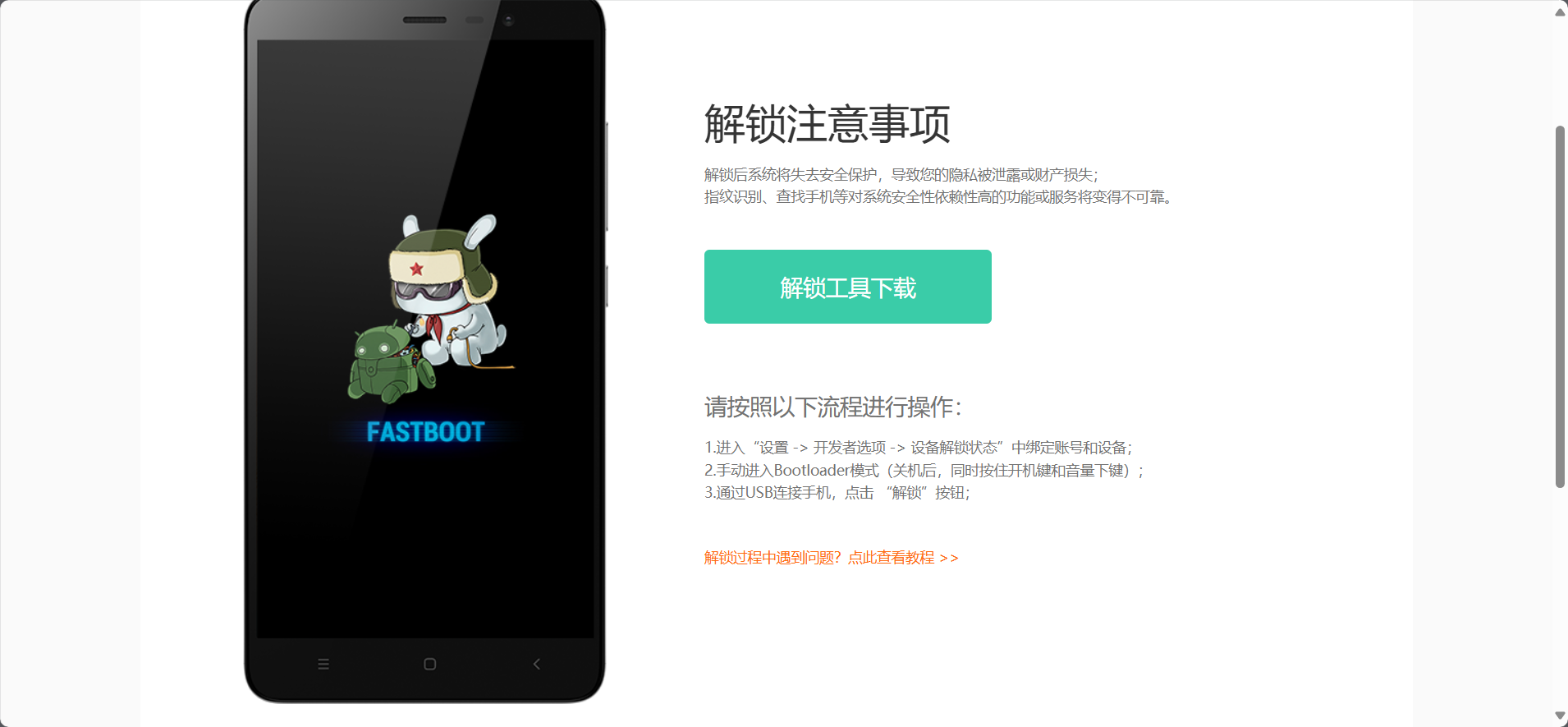
请按照以下流程进行操作:
1.进入“设置 -> 开发者选项 -> 设备解锁状态”中绑定账号和设备;
2.手动进入Bootloader模式(关机后,同时按住开机键和音量下键);
3.通过USB连接手机,点击 “解锁”按钮;
我这边遇到一个问题,就是明明连接了手机,却显示没有连接
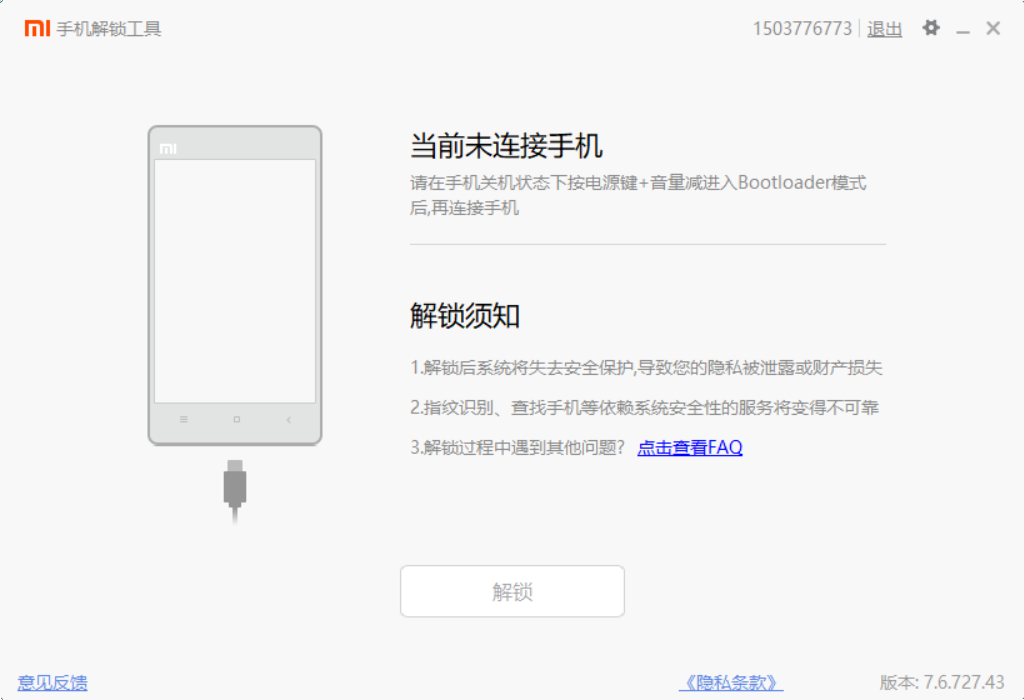
后面我找到这个方法,我使用的是其中的方法三,解决了这个问题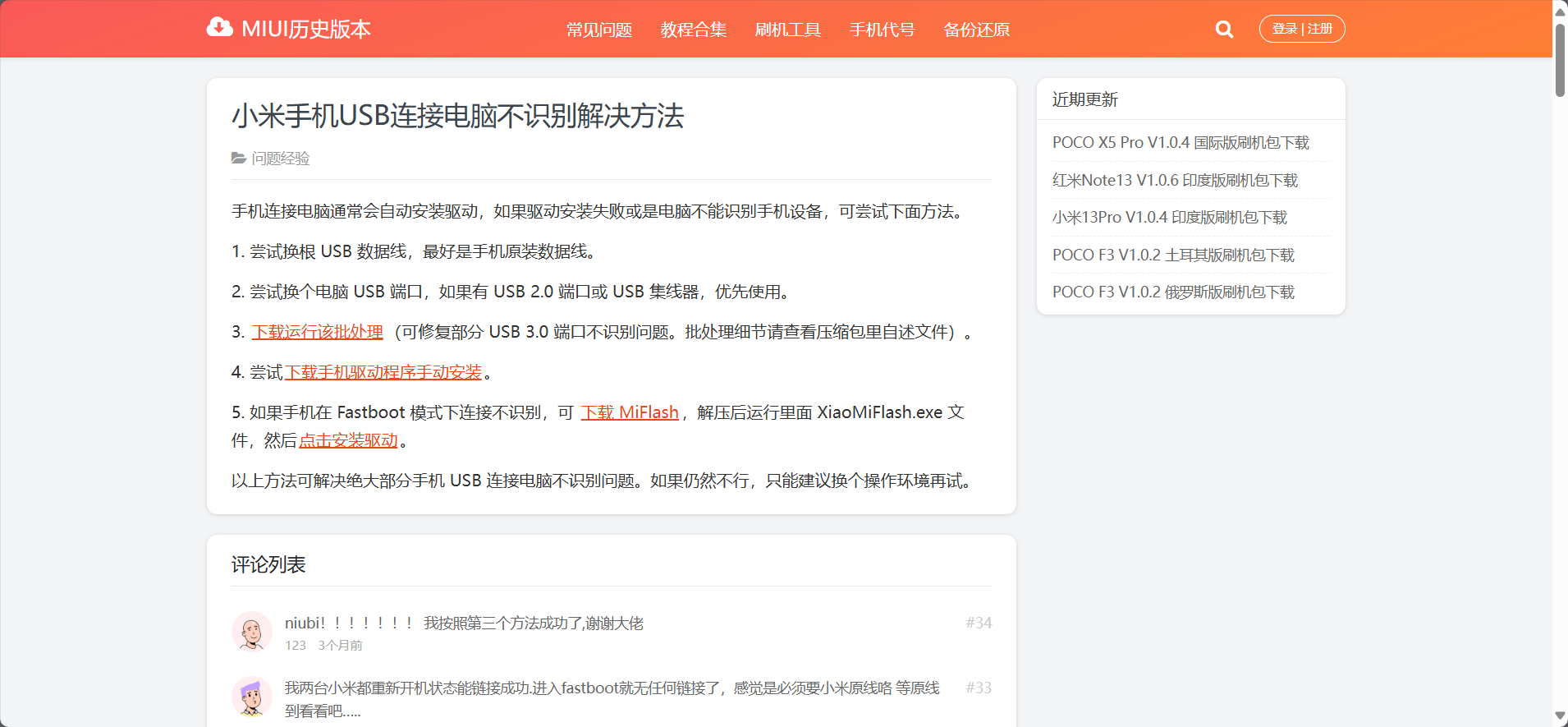
小米手机USB连接电脑不识别解决方法
问题经验
手机连接电脑通常会自动安装驱动,如果驱动安装失败或是电脑不能识别手机设备,可尝试下面方法。
- 尝试换根 USB 数据线,最好是手机原装数据线。
- 尝试换个电脑 USB 端口,如果有 USB 2.0 端口或 USB 集线器,优先使用。
- 下载运行该批处理(可修复部分 USB 3.0 端口不识别问题。批处理细节请查看压缩包里自述文件)。
- 尝试下载手机驱动程序手动安装。
- 如果手机在 Fastboot 模式下连接不识别,可 下载 MiFlash,解压后运行里面 XiaoMiFlash.exe 文件,然后点击安装驱动。
以上方法可解决绝大部分手机 USB 连接电脑不识别问题。如果仍然不行,只能建议换个操作环境再试。
接下来就是根据提示:关机->同时按下音量-和开启键(进入fastboot刷机模式)(线刷模式)->插线
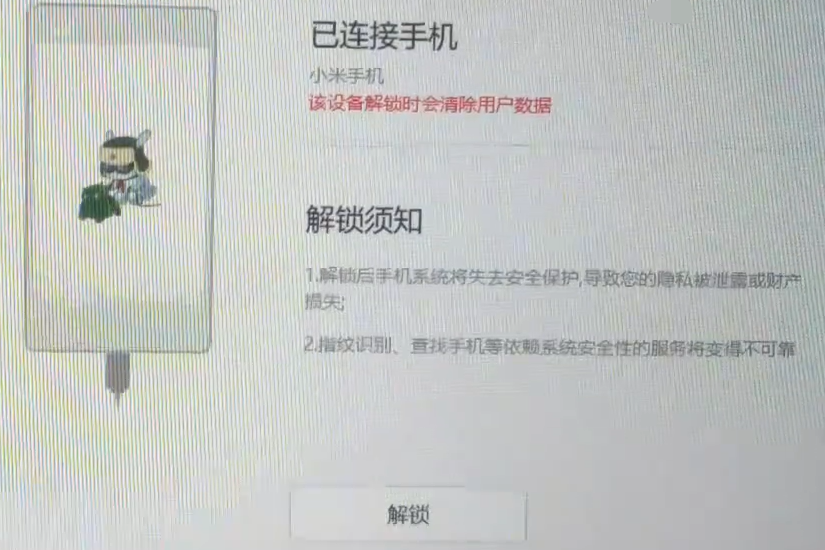
直接点击解锁,接下来的提示一直点击确认解锁即可
显示解锁成功后(拔线),重启即可
第二步刷入Rec
先下载对应的安卓系统的Twrp-Rec包
查看安卓版本:打开设置->我的设备->全部参数->Android版本
我的安卓版本为安卓10,找到对应的包
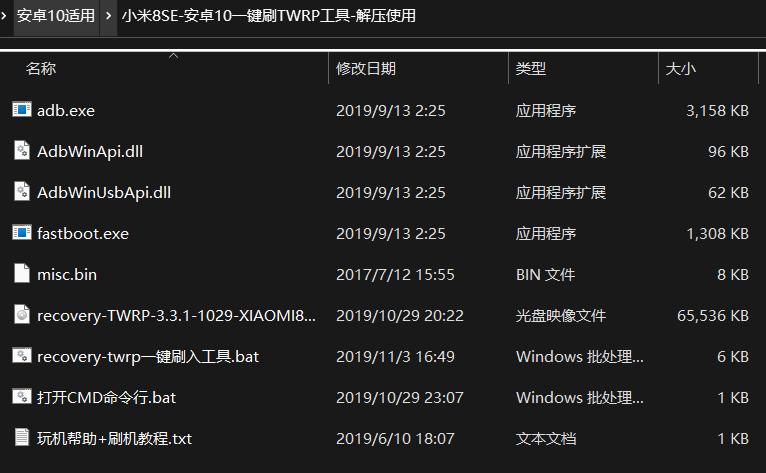
进入fastboot模式(同时按下音量减键和开机键)->插线
双击recovery-twrp一键刷入工具.bat

下一步

下一步

刷入成功

拔线,会自动进TWRP主页面(耐心等待即可)

点击高级->关闭AVB2.0效验(两个都选上)->滑动按钮确认操作->返回TWRP主页面

到此第二步完成。
第三步安装面具(root)
将下载好的面具安装包复制粘贴到小米8SE
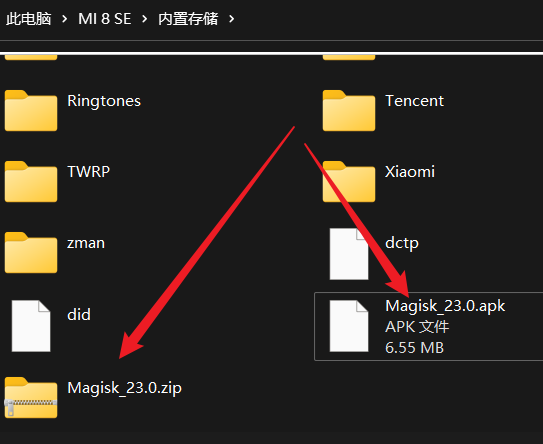
接下来就是安装了,来到TWRP主界面->安装->找到Magisk_23.0.zip(底层包)安装即可
啥也不用管,直接就是滑动按钮确认刷入即可
重启系统,如果发现Magisk无法打开,可能是软件包还没安装好
只需要进入文件管理,找到Magisk_23.0.apk软件包安装即可,到此完成所有步骤
软件链接
面具ZIP数据包及面具APK
下载链接:https://pan.baidu.com/s/1rSI6E2_ilV3OFBTRrNNC1A
提取码:lsp2
小米红米Redmi全系TWRP recovery
下载链接:https://pan.baidu.com/s/1m8vZwyFMT06cr6TA3bXgBQ
提取码:lsp1
以上链接均为此博主提供,如有失效,我也没办法,哈哈哈
相关文章:

小米8SE刷root(面具)
首先准备好一根数据线,一部小米8SE手机,和一台电脑 接下来需要的软件我会给出链接和使用方法,以及分享我遇到的困难和解决方案 下面操作不会的,可以参考这个博主的教程,我也是跟着这个教程刷好的 第一步解锁BL 开启开…...

如果创办Google
本文是一篇演讲稿,来自于《黑客与画家》一书的作者保罗*格雷厄姆,被称为硅谷创业之父。这是他为14至15岁的孩子们做的一次演讲,内容是关于如果他们将来想创立一家创业公司,现在应该做些什么。很多学校认为应该向学生们传授一些有关…...

邦芒职场:揭秘影响你职场收入的九大细节
在职场这个大舞台上,微小的细节往往能决定你收入的多少。以下九大细节,是你职场成功的关键,不容忽视。 1. 形象塑造 在这个注重第一印象的时代,良好的形象是你的第一张名片。精致的妆容、得体的着装,不仅能为你加分&a…...
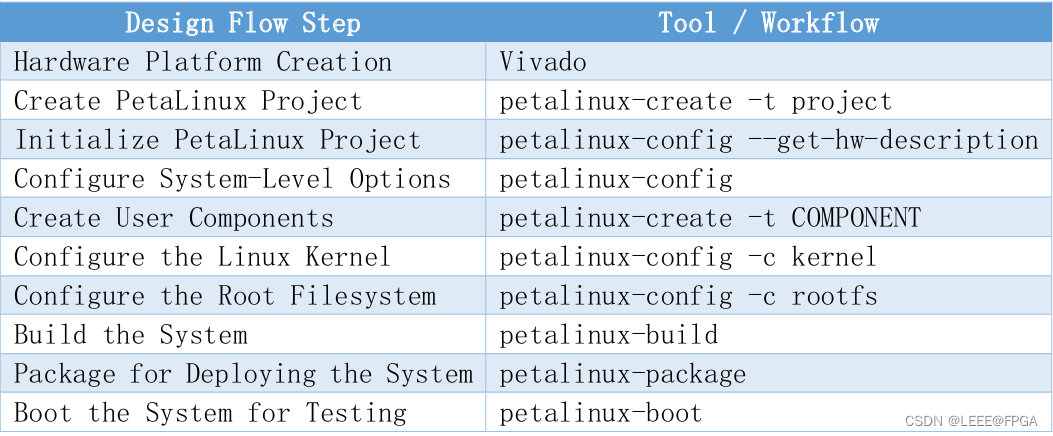
Petalinux 制作ZYNQ镜像文件流程
1概述 在Zynq-7000 SoC中搭建运行Linux,嵌入式软件栈。 处理器系统引导是一个分两个阶段的过程。第一个阶段是一个内部 BootROM,它存储 stage-0 的引导代码。BootROM 在 CPU 0 上执行,CPU 1 执行等待事件(WFE)指令。…...
99%的人都不知道,微信才是真正的学习神器
微信,作为一款全球最受欢迎的社交应用之一,除了聊天、朋友圈、小程序等功能外,还有许多隐藏的学习功能,今天小编就给大家分享10个微信隐藏的学习功能,助您轻松成为学霸。 1、微信笔记 用过代办清单软件的朋友都知道&…...
加速模型训练 GPU cudnn
GPU的使用 在定义模型时,如果没有特定的GPU设置,会使用 torch.nn.DataParallel 将模型并行化,充分利用多GPU的性能,这在加速训练上有显著影响。 model torch.nn.DataParallel(model).cuda() cudnn 的配置: cudnn.…...
《python编程从入门到实践》day40
# 昨日知识点回顾 编辑条目及创建用户账户 暂没能解决bug: The view learning_logs.views.edit_entry didnt return an HttpResponse object. It returned None instead.# 今日知识点学习 19.2.5 注销 提供让用户注销的途径 1.在base.html中添加注销链接 …...

IO多路复用学习笔记
参考资料: 视频1 视频2(本人B站也有发布) 视频3 参考笔记 参考博客...

Ubuntu设置中文输入法教程
在Ubuntu中设置中文输入法非常简单,只需按照以下步骤操作即可。 打开“设置”菜单。在Ubuntu的左上角点击“活动”按钮,然后在弹出的菜单中选择“设置”图标。 进入“区域和语言”设置。在设置菜单中,找到并点击“区域和语言”选项。 添加中…...
)
机器学习之爬山算法(Hill Climbing Algorithm)
爬山算法(Hill Climbing Algorithm)是一种简单而常见的启发式搜索算法,通常用于解决优化问题。它的基本思想类似于登山过程中爬升到山顶的过程,即从一个起始点开始,不断尝试向邻近的点移动,直到找到一个局部最优解。 下面是爬山算法的基本工作流程: 初始化:选择一个初…...
LeetCode - 贪心算法 (Greedy Algorithm) 集合 [分配问题、区间问题]
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/139242199 贪心算法,是在每一步选择中,都采取当前状态下,最好或最优(即最有利)的选择&…...
Linux中ftp配置
一、ftp协议 1、端口 ftp默认使用20、21端口 20端口用于建立数据连接 21端口用于建立控制连接 2、ftp数据连接模式 主动模式:服务器主动发起数据连接 被动模式:服务器被动等待数据连接 二、ftp安装 yum install -y vsftpd #---下…...
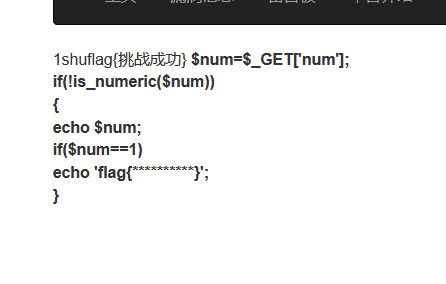
BWVS 靶场测试
一、PHP弱类型 is_numeric() 输入:127.0.0.1/BWVS/bug/php/code.php # 1、源代码分析 如果num不是数字,那么就输出num,同时如果num1,就输出flag。即num要是字符串又要是数字 # 2、函数分析: is_numeric()函数&…...
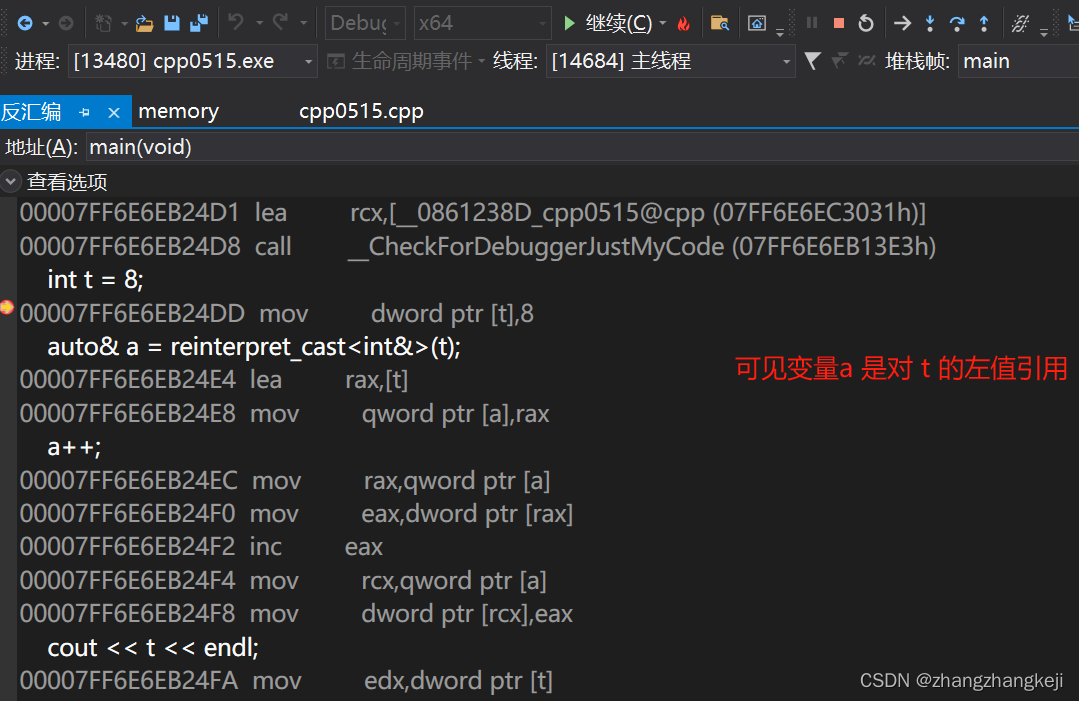
c++ 里重解释转换之于引用 reinterpret_cast< long >
今天遇到了这一很新奇的写法。模糊中记得王老师也这么讲过。c 里四大转换。把数据重解释为原来数据的引用。虽然也可以直接定义对变量的引用。测试如下: 咱们从反汇编再了解下 c 编译器是怎么处理这种写法的: 谢谢...
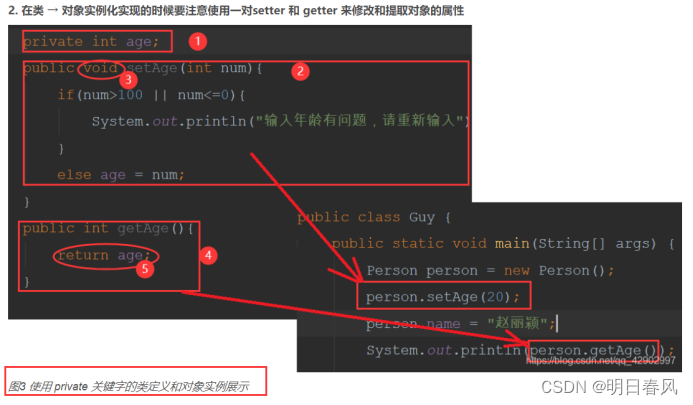
JAVASE2
封装的步骤: 1、所有属性私有化,使用private关键字进行修饰,private表示私有的,修饰的所有数据只能在本类中访问 2、对外提供简单入口:比如说被private修饰的成员变量,在其他类中只能通过getXxx/setXxx方法…...

ora-00392 ora-00312错误处理
检查当前日志组状态 对日志组进行clear操作 重新开库无报错...

网页、h5默认滚动条样式重构
文章目录 前言一、使用步骤1、在想要滚动的元素上设置相应的css类名2.设置样式 总结 前言 此文章用于,让我自己快速设置 浏览器、h5 默认滚动条样式…… 一、使用步骤 1、在想要滚动的元素上设置相应的css类名 代码如下: <div class"list scro…...

香橙派AIpro测评上手指南
一、前言 首先非常荣幸受到邀请参加本次香橙派开发板的测评活动,除了令人眼前一亮,做工非常精细的开发板,举办方还非常贴心地准备了散热套件,以及烧录好系统的TF卡,甚至准备了电源适配器,数据线࿱…...

GBDT 算法【python,机器学习,算法】
GBDT 即 Gradient Boosting Decision Tree 梯度提升树, 是一种迭代的决策树算法,又叫 MART(Multiple Additive Regression Tree), 它通过构造一组弱的学习器(树),然后把多棵决策树的结果累加起来作为最终的预测输出。该算法将决策…...
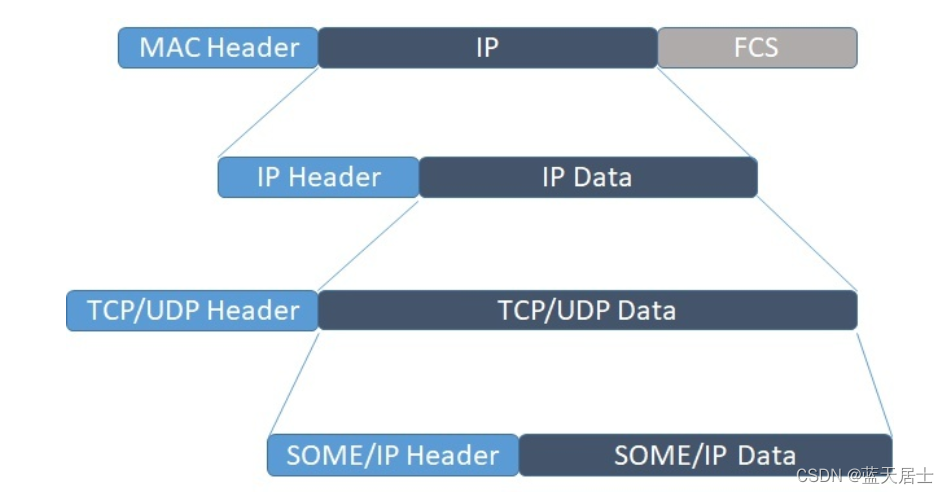
软考 系统架构设计师系列知识点之SOME/IP与DDS(3)
接前一篇文章:软考 系统架构设计师系列知识点之SOME/IP与DDS(2) 本文内容参考: 车载以太网 - SOME/IP简介_someip-CSDN博客 https://zhuanlan.zhihu.com/p/369422441 什么是SOME/IP?_someip-CSDN博客 SOME/IP 详解系列&#…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
