计算机网络:RIP协议以及距离向量算法
RIP协议
-
RIP是一种分布式的基于适量向量的路由选择协议,最大优点是简单。要求网络中的每一个路由器都要维护从它自己到其他每一个目的网络的唯一最佳(最短)距离记录,最多包含15个路由器,距离为16就表示网络不可达,RIP协议只适合小型互联网。
-
RIP协议维护路由表:
 1.仅和相邻的路由器交换信息(自己的路由表)。
1.仅和相邻的路由器交换信息(自己的路由表)。
2.每30秒交换路由信息,然后根据路由信息更新路由表;如果超过180秒,没有收到邻居的路由信息,则认为该邻居没了,更新自己的路由表。 -
收敛:开始时,路由器只知道直接相连的网络信息,接着与每一个相邻路由器交换路由信息并更新路由表。经过若干次更新后,所有路由器都知道到达本自治系统任何一个网络的最短距离和下一跳路由器的地址。
距离向量算法
-
修改相邻路由器发来的RIP报文中的所有表项:对于地址是X的相邻路由器发来的RIP报文,修改报文中的所有项目,即把下一跳的地址改为X,所有距离加1。

-
对修改后的RIP报文中的每一项,进行以下步骤:
1.若R1路由器中没有到达Net3的表项,则将直接将收到的表项加入R1路由表。
2.若R1路由器中有到达Net3的表项,则查看路由表中下一跳路由器地址:若下一跳是X,则用收到表项替换原来的表项;若下一跳不是X,走原来的距离比走X的距离远则更新,否则不做处理。 -
如果180秒还没收到相邻路由器X发送出的路由消息,则把路由器X记为不可达,把距离设置为16。
-
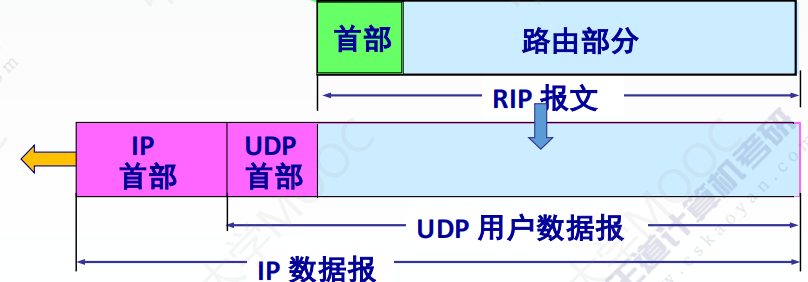
RIP是应用层协议,且最多传递25个路由信息。
相关文章:

计算机网络:RIP协议以及距离向量算法
RIP协议 RIP是一种分布式的基于适量向量的路由选择协议,最大优点是简单。要求网络中的每一个路由器都要维护从它自己到其他每一个目的网络的唯一最佳(最短)距离记录,最多包含15个路由器,距离为16就表示网络不可达&…...
[数据结构与算法(严蔚敏 C语言第二版)]第1章 绪论(课后习题+答案解析)
1. 简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。 数据 数据是客观事物的符号表示,是所有能输人到计算机中并被计算机程序处理的符号的总称。数据是信息的载体,能够被计算机识别、存储和加工 数据元素…...

JS_countup.js 的简单使用,数字滚动效果
countup.js countup.js 是一个轻量级,无依赖的JavaScript类,通过简单的设置就可以达到数字滚动的效果 官网:https://inorganik.github.io/countUp.js/ 源码 var CountUpfunction(target,startVal,endVal,decimals,duration,options){var …...

【C++知识点】STL 容器总结
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:C/C知识点 📣专栏定位:整理一下 C 相关的知识点,供大家学习参考~ ❤️如果有收获的话,欢迎点赞👍…...
)
C++---背包模型---装箱问题(每日一道算法2023.3.9)
注意事项: 本题是"动态规划—01背包"的扩展题,dp和优化思路不多赘述。 题目: 有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积(正整数)。 要求 n 个物品中,任取若…...
if-else if与switch的练习1:输入两个数,输出两个数的加减乘除的值
1.if-else if的练习 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice…...

【教程】你现在还不知道微软的New Bing?你out了,快点进来看
哈喽啊,大家好,好久不见,我是木易巷! 不禁感叹,AI人工智能时代真的已经来临! 目前,谷歌和微软就各自面向大众的产品发布了重大公告。谷歌推出了一款名为Bard实验性对话式 AI 服务,而…...

https流程
ssl加密协议包含以下4个步骤 1、服务器去第三方机构注册生成证书,第三方机构非对称加密生成公钥私钥,给服务器一个私钥,证书包含了公钥。 2、客户端向服务器索要证书 3、客户端向第三方机构验证证书 4、客户端对称加密生成密钥,在…...

python魔法方法
Python中的魔法方法(也称为特殊方法或双下划线方法)是在类定义中使用的一些特殊的函数,可以使用dir方法查询。它们以双下划线开头和结尾,例如__init__和__str__。这些方法被Python解释器用于执行特定的操作,例如实例化对象、字符串…...
软件测试员如何进行产品测试?
一般来讲,当软件成为一个成功的产品后,产品测试工作就会复杂很多。比如拥有的用户量大,迭代频繁,测试的周期短,重复性强。面对紧张复杂的产品测试工作,软件测试员应怎样完成这一系列的测试工作呢࿱…...
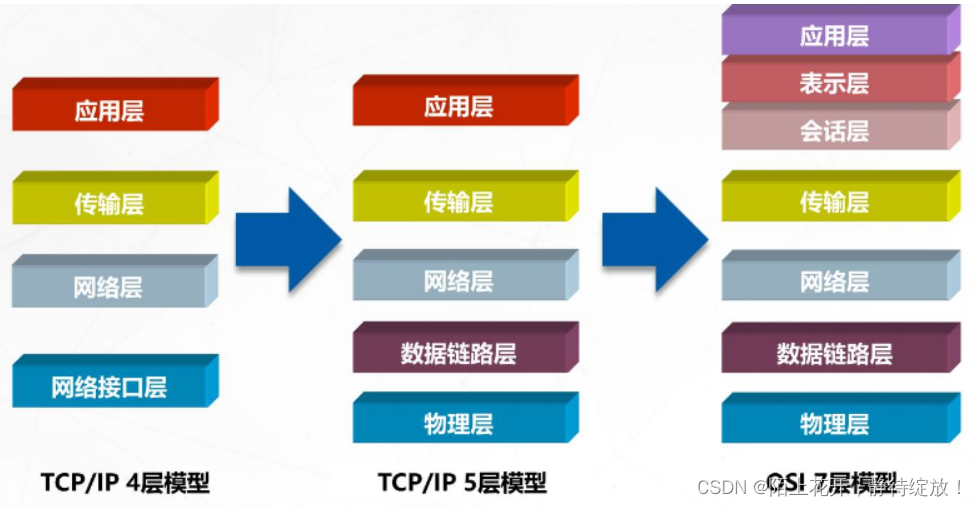
计算机网络基础知识点【1】
文章目录计算机网络第一章 计算机网络参考模型1.计算机网络为什么需要分层?1.1 分层思想1.2 分层好处2.OSI七层模型2.1 OSI七层模型总结2.2 OSI七层工作原理2.3 数据封装与解封装2.4 计算机网络常用协议3.TCP/IP参考模型3.1 什么是TCP/IP协议3.2 TCP/IP协议族的组成…...

c++ 中标准库类型 string 详解
👁🗨👁🗨 前言 标准库类型string 表示可变长的字符序列,使用string 类型必须首先包含string 头文件。string 定义在命名空间std 中。 定义和初始化 string 对象 首先说明如何初始化对象是由类本身决定的࿰…...
)
Html新增属性之拖拽(drag)
元素在拖放过程中触发的事件 HTML5中,只要将元素的 draggable 属性设置为 true 就可以实现拖放功能,在拖放过程中,触发了多个事件,如下: dragstart:事件主体是被拖放元素,在开始拖放被拖放元素时触发。dra…...
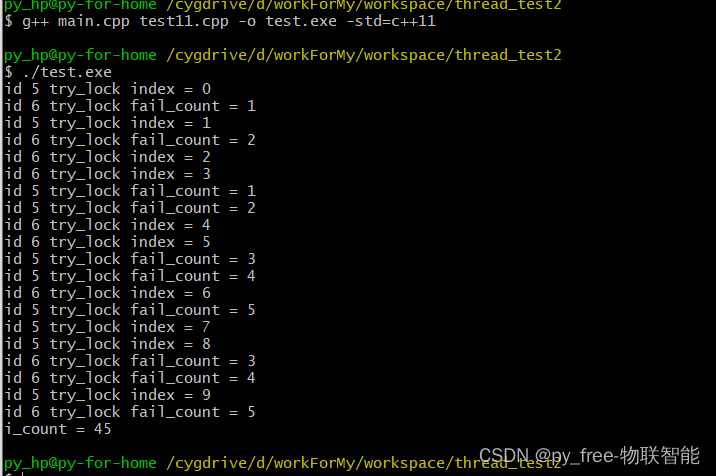
C/C++开发,无可避免的多线程(篇二).thread与其支持库
一、原子类型与原子操作 1.1 原子类型与操作介绍 在前一篇博文中,多线程交互示例代码中,给出了一个原子类型定义: // 原子数据类型 atomic_llong total {0}; 那么什么事原子数据类型呢,和c的基础数据类型有什么不同呢:…...
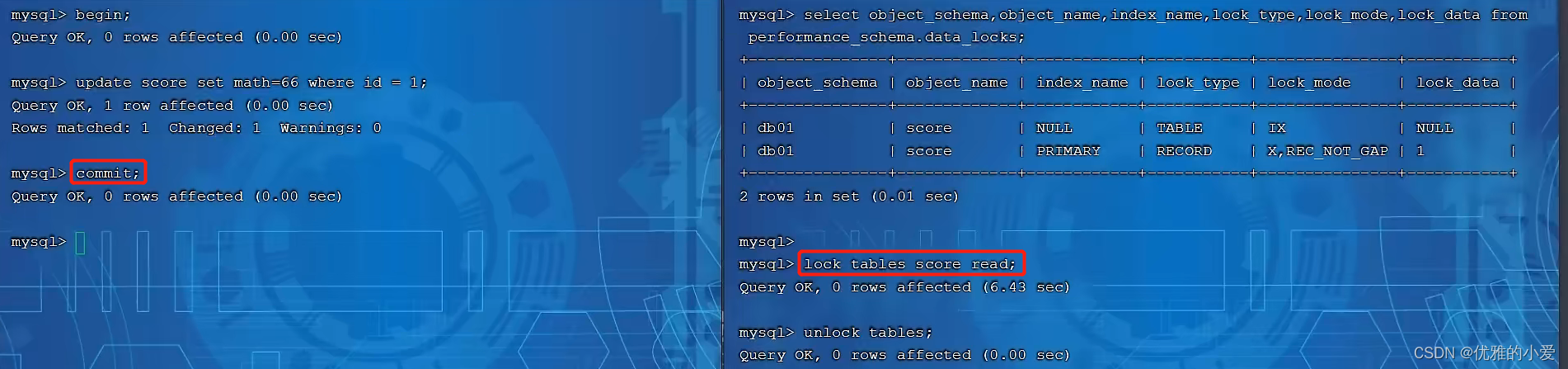
mysql数据库之表级锁
表级锁,每次操作锁住整张表。锁定粒度大,发生所冲突的概率最高,并发度最低。应用在myisam、innodb、bdb等存储引擎中。 一、表级锁分类。 1、表锁 2、元数据锁(meta data lock,MDL) 3、意向锁 二、表锁…...
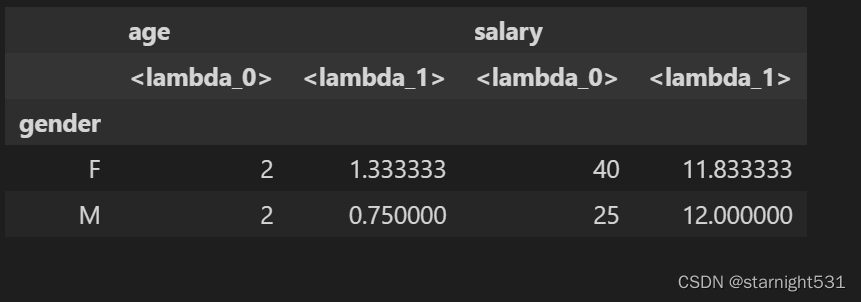
Python - Pandas - 数据分析(2)
Pandas数据分析2前言常用的21种统计方法describe():numeric_only:偏度skewness:功能:含义:计算公式:演示:峰度值:用途:数值:计算公式:演示&#x…...

我的十年编程路 2019年篇
随着2018年,三星天津研究院的裁撤,我选择了到广州的三星研究院工作,与最心爱的她开始一起生活。 这一年的开始,我注册了博客园。和2014年类似,在刚注册不久,我写了一篇题为《全新开始,全心出发…...

(蓝桥真题)剪格子(搜索+剪枝)
样例1输入: 3 3 10 1 52 20 30 1 1 2 3 样例1输出: 3 样例2输入: 4 3 1 1 1 1 1 30 80 2 1 1 1 100 样例2输出: 10 分析:这道题目我们直接从(1,1)点开始进行dfs搜索即可,但是需要注意一点的是我们搜…...

Kalman Filter in SLAM (3) ——Extended Kalman Filter (EKF, 扩展卡尔曼滤波)
文章目录1. 线性系统的 Kalman Filter 回顾2. Extended Kalman Filter 之 DR_CAN讲解笔记2.1. 非线性系统2.2. 非线性系统线性化2.2.1. 状态方程f(xk)f(x_k)f(xk)在上一次的最优估计状态x^k−1\hat{x}_{k-1}x^k−1处线性化2.2.2. 观测方程h(xk)h(x_k)h(xk)在这一次的预测…...

关于vertical-align的几问
vertical-align属性可以给我讲解一下吗? 当使用table-cell布局或inline元素时,可以使用CSS的vertical-align属性控制元素的垂直对齐方式。该属性可应用于元素本身以及其父元素(例如,td、th、tr和table)。 以下是vertic…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
