C++---背包模型---装箱问题(每日一道算法2023.3.9)
注意事项:
本题是"动态规划—01背包"的扩展题,dp和优化思路不多赘述。
题目:
有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积(正整数)。
要求 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
输入格式
第一行是一个整数 V,表示箱子容量。
第二行是一个整数 n,表示物品数。
接下来 n 行,每行一个正整数(不超过10000),分别表示这 n 个物品的各自体积。
输出格式
一个整数,表示箱子剩余空间。
数据范围
0<V≤20000,
0<n≤30
输入:
24
6
8
3
12
7
9
7
输出:
0
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;const int N = 20010;
int n, m;
int v[N], f[N];int main () {cin >> m >> n;for (int i = 1; i<=n; i++) cin >> v[i];//01背包,滚动数组优化模板for (int i = 1; i<=n; i++) {for (int j = m; j>=v[i]; j--) {f[j] = max(f[j], f[j-v[i]] + v[i]); //直接将v[i]本身当作价值,替换掉w[i]}}cout << m-f[m]; //求的是总体积减去最大体积,即为剩余体积return 0;
}
思路:
v[i]保持原位时看作 物品体积,在替换掉w[i]时看作 物品价值。
其实就是将01背包中的 ”物品价值“ 等价替换为 “物品体积”,其余部分不变即可。
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流
相关文章:
)
C++---背包模型---装箱问题(每日一道算法2023.3.9)
注意事项: 本题是"动态规划—01背包"的扩展题,dp和优化思路不多赘述。 题目: 有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积(正整数)。 要求 n 个物品中,任取若…...
if-else if与switch的练习1:输入两个数,输出两个数的加减乘除的值
1.if-else if的练习 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice…...

【教程】你现在还不知道微软的New Bing?你out了,快点进来看
哈喽啊,大家好,好久不见,我是木易巷! 不禁感叹,AI人工智能时代真的已经来临! 目前,谷歌和微软就各自面向大众的产品发布了重大公告。谷歌推出了一款名为Bard实验性对话式 AI 服务,而…...

https流程
ssl加密协议包含以下4个步骤 1、服务器去第三方机构注册生成证书,第三方机构非对称加密生成公钥私钥,给服务器一个私钥,证书包含了公钥。 2、客户端向服务器索要证书 3、客户端向第三方机构验证证书 4、客户端对称加密生成密钥,在…...

python魔法方法
Python中的魔法方法(也称为特殊方法或双下划线方法)是在类定义中使用的一些特殊的函数,可以使用dir方法查询。它们以双下划线开头和结尾,例如__init__和__str__。这些方法被Python解释器用于执行特定的操作,例如实例化对象、字符串…...
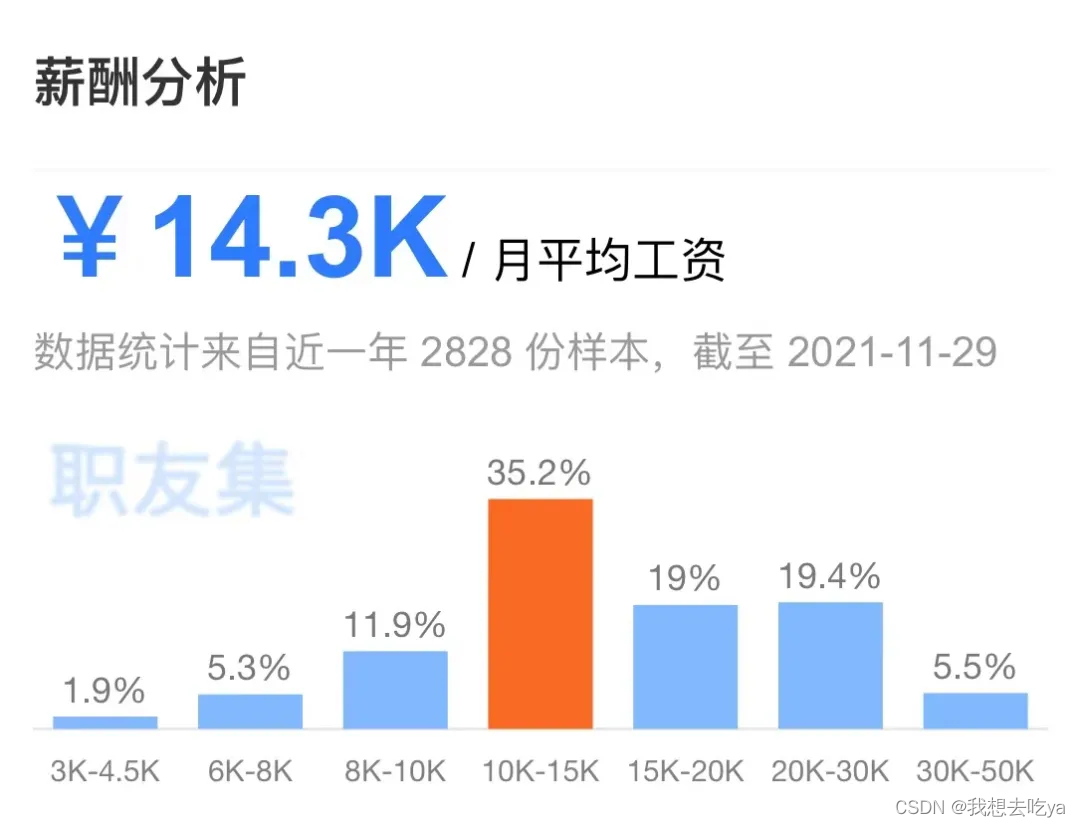
软件测试员如何进行产品测试?
一般来讲,当软件成为一个成功的产品后,产品测试工作就会复杂很多。比如拥有的用户量大,迭代频繁,测试的周期短,重复性强。面对紧张复杂的产品测试工作,软件测试员应怎样完成这一系列的测试工作呢࿱…...
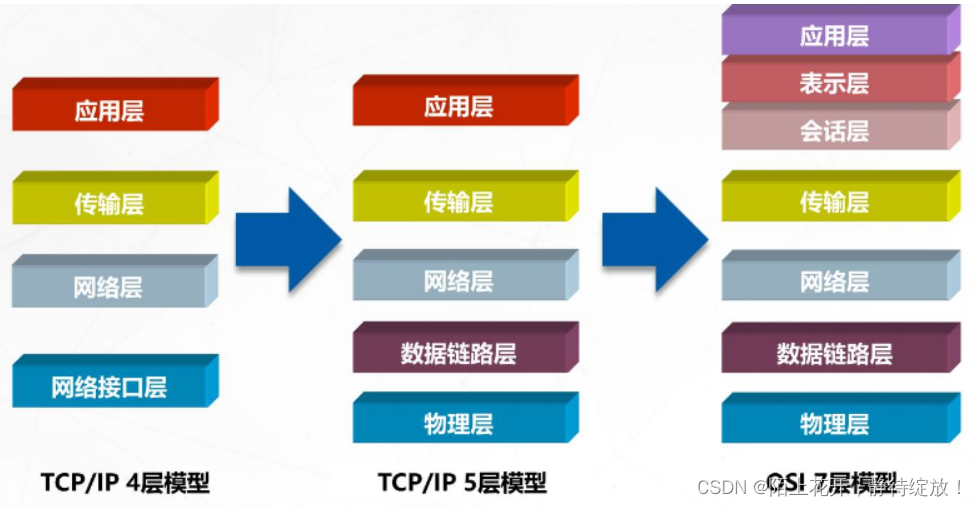
计算机网络基础知识点【1】
文章目录计算机网络第一章 计算机网络参考模型1.计算机网络为什么需要分层?1.1 分层思想1.2 分层好处2.OSI七层模型2.1 OSI七层模型总结2.2 OSI七层工作原理2.3 数据封装与解封装2.4 计算机网络常用协议3.TCP/IP参考模型3.1 什么是TCP/IP协议3.2 TCP/IP协议族的组成…...

c++ 中标准库类型 string 详解
👁🗨👁🗨 前言 标准库类型string 表示可变长的字符序列,使用string 类型必须首先包含string 头文件。string 定义在命名空间std 中。 定义和初始化 string 对象 首先说明如何初始化对象是由类本身决定的࿰…...
)
Html新增属性之拖拽(drag)
元素在拖放过程中触发的事件 HTML5中,只要将元素的 draggable 属性设置为 true 就可以实现拖放功能,在拖放过程中,触发了多个事件,如下: dragstart:事件主体是被拖放元素,在开始拖放被拖放元素时触发。dra…...
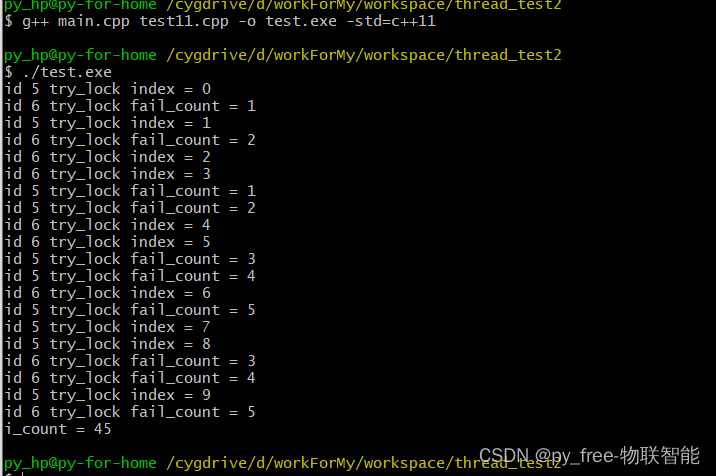
C/C++开发,无可避免的多线程(篇二).thread与其支持库
一、原子类型与原子操作 1.1 原子类型与操作介绍 在前一篇博文中,多线程交互示例代码中,给出了一个原子类型定义: // 原子数据类型 atomic_llong total {0}; 那么什么事原子数据类型呢,和c的基础数据类型有什么不同呢:…...
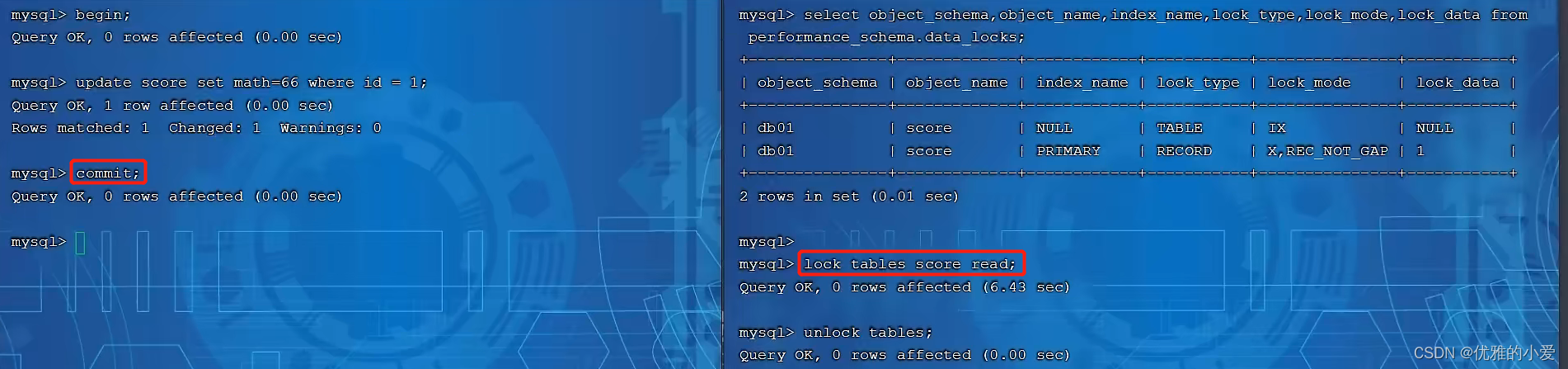
mysql数据库之表级锁
表级锁,每次操作锁住整张表。锁定粒度大,发生所冲突的概率最高,并发度最低。应用在myisam、innodb、bdb等存储引擎中。 一、表级锁分类。 1、表锁 2、元数据锁(meta data lock,MDL) 3、意向锁 二、表锁…...
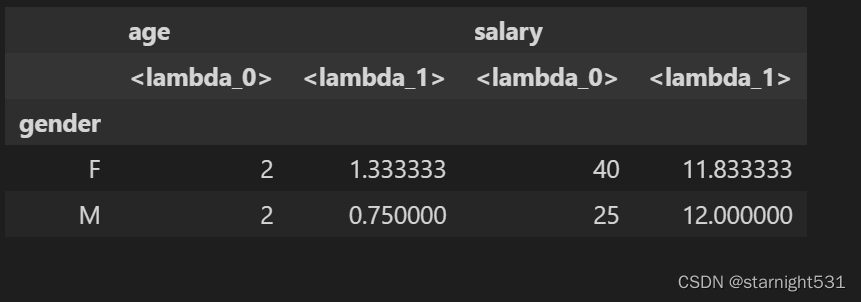
Python - Pandas - 数据分析(2)
Pandas数据分析2前言常用的21种统计方法describe():numeric_only:偏度skewness:功能:含义:计算公式:演示:峰度值:用途:数值:计算公式:演示&#x…...

我的十年编程路 2019年篇
随着2018年,三星天津研究院的裁撤,我选择了到广州的三星研究院工作,与最心爱的她开始一起生活。 这一年的开始,我注册了博客园。和2014年类似,在刚注册不久,我写了一篇题为《全新开始,全心出发…...

(蓝桥真题)剪格子(搜索+剪枝)
样例1输入: 3 3 10 1 52 20 30 1 1 2 3 样例1输出: 3 样例2输入: 4 3 1 1 1 1 1 30 80 2 1 1 1 100 样例2输出: 10 分析:这道题目我们直接从(1,1)点开始进行dfs搜索即可,但是需要注意一点的是我们搜…...

Kalman Filter in SLAM (3) ——Extended Kalman Filter (EKF, 扩展卡尔曼滤波)
文章目录1. 线性系统的 Kalman Filter 回顾2. Extended Kalman Filter 之 DR_CAN讲解笔记2.1. 非线性系统2.2. 非线性系统线性化2.2.1. 状态方程f(xk)f(x_k)f(xk)在上一次的最优估计状态x^k−1\hat{x}_{k-1}x^k−1处线性化2.2.2. 观测方程h(xk)h(x_k)h(xk)在这一次的预测…...

关于vertical-align的几问
vertical-align属性可以给我讲解一下吗? 当使用table-cell布局或inline元素时,可以使用CSS的vertical-align属性控制元素的垂直对齐方式。该属性可应用于元素本身以及其父元素(例如,td、th、tr和table)。 以下是vertic…...

【拜占庭将军问题】这一计谋,可以让诸葛丞相兴复汉室
我们都知道,诸葛亮第一次北伐是最可能成功的,魏国没有防备,还策反了陇西,陇西有大量的马匹可以装备蜀国骑兵,可惜街亭一丢,那边就守不住了 当时我不在,只能作诗一首~ 如果穿越过去,…...
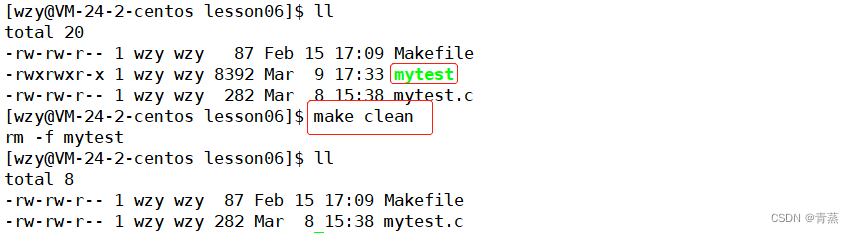
【Linux】 -- make/Makefile
目录 Linux项目自动化构建工具 – make/Makefile 背景 依赖关系和依赖方法 多文件编译 项目清理 make原理 Linux项目自动化构建工具 – make/Makefile 背景 一个工程的源文件不计其数 按照其类型、功能、模块分别放在若干个目录当中 Makefile定义了一系列的规则来指定&…...

Forter 对支付服务商应对欺诈的四个建议和Gartner的两个关键结论
Gartner新版2023年度《线上欺诈检测市场指南》发布恰逢其时-企业正面临来自专业黑产和欺诈者与日俱增的压力。而在2023年,许多商户将调整反欺诈策略,对拒付率和转化率进行更严格的监测,以最大限度减少损失并增加营收。以下是Gartn…...
——ANR监听方案之IdleHandler)
ANR系列(二)——ANR监听方案之IdleHandler
前言 关于IdleHandler,比较多同学错误地认为,这个Handler的作用是主线程空闲状态时才执行它,那么用它做一些耗时操作也没所谓。可是IdleHandler在主线程的MessageQueue中,执行queueIdle()默认当然也是执行在主线程中的࿰…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
