【拜占庭将军问题】这一计谋,可以让诸葛丞相兴复汉室
我们都知道,诸葛亮第一次北伐是最可能成功的,魏国没有防备,还策反了陇西,陇西有大量的马匹可以装备蜀国骑兵,可惜街亭一丢,那边就守不住了
当时我不在,只能作诗一首~

如果穿越过去,我将会向丞相献上一计,别说街亭,直接拿下长安,先看地图
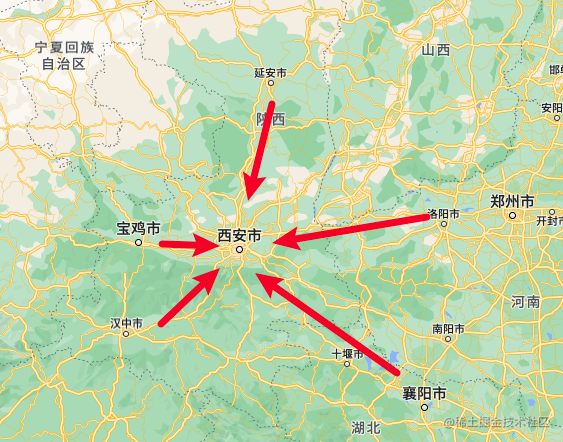
从延安,洛阳,策反魏国州长,让他们出兵。然后再结盟孙权,让他从久攻不下的合肥调来800精兵从襄阳进攻,让魏延从宝鸡出兵,自己率领大军从汉中进发
五路攻击,光围都能把长安围死
但是这个时候你可能会说:天方夜谭,且不说孙权,你怎么能确保洛阳和延安的兵听你的,而不是反贼?
这个呢,就需要我们今天要讲的问题,也称为【拜占庭将军问题】,多节点场景,没有中心化的协调,而且其中可能出现不可靠结点的情况下,如何保证大家行动的统一性?
我们先约定一些共识:
- 一个丞相发送指令,四个将军接收
- 所有人都可能是反贼
- 反贼回复的指令和丞相的相反
现在我们模拟一个场景,必须要五路进发才能够打下长安,其中有反贼。当主路——也就是诸葛亮的那一路发出“进攻”指令时,另外四路的将军会收到,同时会向其他三路求证,如果进攻指令数过半数,就会进攻。但是反贼会回复别的将军【撤退】指令
如果反贼过多,导致【撤退】指令过多,所有的将军都不会出动,丞相只能自己北伐了
-
那么此时忠反比多少才合适呢?
关键在于,即使有反贼存在,只要忠臣数量足够多,就可以保证最终的决策是正确的。
这是因为反贼无法破坏所有将军之间的通信,因此忠臣可以通过相互交流,确定反贼的存在并排除他们的虚假消息。最终的决策取决于忠臣的数量,通常情况下,当忠臣数量超过总将军数量的三分之二时,算法可以保证正确性。
-
那么为什么是三分之二呢?不是更多或者更少?
假设发指令的是丞相,其他为将军,总数为n, 反贼数为m,
其中每一个将军做判断的依据是接受到的指令取多数,
每个将军自己在判断时,只会考虑别的将军和丞相的指令,排除自己,所以此时有n - 1个指令,那么会出现 m 个假指令和n - m - 1 个真指令
只要保证 n - m - 1 > m,也就是 n > 2m + 1即可
这是基本情况,当n = 3, m = 1时,满足n > 2m + 1,但是忠臣只会收到一个真指令和一个假指令,无法判断丞相或者另一个将军谁是反贼,所以为了确保取
n > 3m,也就是忠臣占2/3多数
下面是一个简单的Java代码示例,演示了如何解决这个问题。
假设有6个将军,其中两个是反贼。每个将军都有一个唯一的ID和一个决策(attack或retreat)。这些将军之间通过消息传递来达成共识。
import java.util.Arrays;
import java.util.Random;
public class ByzantineGenerals {
private static final int NUM_GENERALS = 6;
private static final int REPEAT = 5;static int traitor;static int traitor2;public static void main(String[] args) {
String[] orders = new String[NUM_GENERALS]; // 命令集合for (int p = 0; p < REPEAT; p++) {traitor = new Random().nextInt(NUM_GENERALS - 1);traitor2 = new Random().nextInt(NUM_GENERALS);if (traitor == traitor2) traitor2 += 1;for (int i = 0; i < NUM_GENERALS; i++) {orders[i] = (i == traitor || i == traitor2) ? "retreat" : "attack";}
System.out.println("orders" + Arrays.toString(orders));boolean finalDecision = computeFinalDecision(orders);System.out.println("Final decision: " + (finalDecision ? "attack" : "retreat"));System.out.println();}}
private static boolean computeFinalDecision(String[] orders) {boolean[] decisions = new boolean[NUM_GENERALS];for (int i = 0; i < NUM_GENERALS; i++) {if (i == traitor || i == traitor2) {decisions[i] = (new Random().nextBoolean());} else {boolean[] receivedOrders = new boolean[NUM_GENERALS - 1];int index = 0;for (int j = 0; j < NUM_GENERALS; j++) {if (j != i) {receivedOrders[index++] = (orders[j].equals("attack")); // 每一位将军收集命令}}decisions[i] = computeDecision(receivedOrders);}}return computeDecision(decisions);}
private static boolean computeDecision(boolean[] decisions) {// Compute the majority decisionint numTrue = 0;int numFalse = 0;for (boolean decision : decisions) {if (decision) {numTrue++;} else {numFalse++;}}return (numTrue > numFalse);}
}
在上面的示例代码中,我们模拟了一个有6个将军的场景,并随机指定两个将军为反贼。每个将军都有一个决策,攻击或撤退。如果将军是反贼,他将发送虚假的命令,否则,将军将发送他真正的命令。在每个将军之间进行消息传递后,每个将军都会收到其他将军发送的命令。如果将军是反贼,他可能会给每个将军发送不同的命令,而忠臣将发送相同的命令。最后,每个将军都会将他们收到的命令和自己的命令一起计算出一个最终的决策,并将它们合并成一个共同的决策。
在计算决策的过程中,我们使用了一个简单的投票算法。我们将每个将军的决策转换为一个布尔值(attack为true,retreat为false),然后计算出这些布尔值中出现次数最多的值。如果attack出现的次数比retreat多,则我们最终的决策为attack,否则为retreat。
输出之一如下
orders[retreat, retreat, attack, attack, attack, attack]
Final decision: attack
orders[attack, attack, retreat, retreat, attack, attack]
Final decision: attack
orders[attack, attack, attack, retreat, retreat, attack]
Final decision: attack
orders[attack, attack, retreat, attack, retreat, attack]
Final decision: attack
orders[retreat, attack, attack, attack, attack, retreat]
Final decision: attack
可以看到在6个将军2个反贼下是符合 n > 2m + 1的场景,所以大家都是进攻
在n = 3, m = 1时,n > 2m + 1需要替换为 n > 3m
保险起见取 n > 3m即可
在我看来,这个问题是对投票解决问题的有效性和科学性很有力的佐证,比如选举,即使人民中藏了很多间谍或者是愚昧的人,但是只要正常人占了2/3以上,就可以确保这一制度的稳定与务实。

同时,如果诸葛亮使用我的计策,五路取长安,那么完全可以兴复汉室,还于旧都。剩下的只需要解决这一计策上面的两朵小乌云即可
- 如何防止孙权背刺
- 如何策反魏国两个地方的军队
相关文章:

【拜占庭将军问题】这一计谋,可以让诸葛丞相兴复汉室
我们都知道,诸葛亮第一次北伐是最可能成功的,魏国没有防备,还策反了陇西,陇西有大量的马匹可以装备蜀国骑兵,可惜街亭一丢,那边就守不住了 当时我不在,只能作诗一首~ 如果穿越过去,…...
【Linux】 -- make/Makefile
目录 Linux项目自动化构建工具 – make/Makefile 背景 依赖关系和依赖方法 多文件编译 项目清理 make原理 Linux项目自动化构建工具 – make/Makefile 背景 一个工程的源文件不计其数 按照其类型、功能、模块分别放在若干个目录当中 Makefile定义了一系列的规则来指定&…...

Forter 对支付服务商应对欺诈的四个建议和Gartner的两个关键结论
Gartner新版2023年度《线上欺诈检测市场指南》发布恰逢其时-企业正面临来自专业黑产和欺诈者与日俱增的压力。而在2023年,许多商户将调整反欺诈策略,对拒付率和转化率进行更严格的监测,以最大限度减少损失并增加营收。以下是Gartn…...
——ANR监听方案之IdleHandler)
ANR系列(二)——ANR监听方案之IdleHandler
前言 关于IdleHandler,比较多同学错误地认为,这个Handler的作用是主线程空闲状态时才执行它,那么用它做一些耗时操作也没所谓。可是IdleHandler在主线程的MessageQueue中,执行queueIdle()默认当然也是执行在主线程中的࿰…...
)
数学小课堂:数学和自然科学的关系(数学方法,让自然科学变成科学体系。)
文章目录 引言I 数学方法,让自然科学变成科学体系。1.1 天文学1.2 博物学1.3 化学1.4 医药学1.5 物理学II 自然科学的升华过程III 数学方法的意义引言 19世纪初,英国人把采用实验的方法,系统地构造和组织知识,解释和预测自然的学问称为科学。 科学研究的是自然现象和自然…...

[蓝桥杯 2020 省 A1] 分配口罩
思路比较容易想到,因为口罩全部只有15批,因此直接暴力dfs搜索即可 //dfs #include<bits/stdc.h> using namespace std; int ans 9999; int num[] {9090400, 8499400, 5926800, 8547000, 4958200, 4422600, 5751200, 4175600, 6309600, 5865200, …...
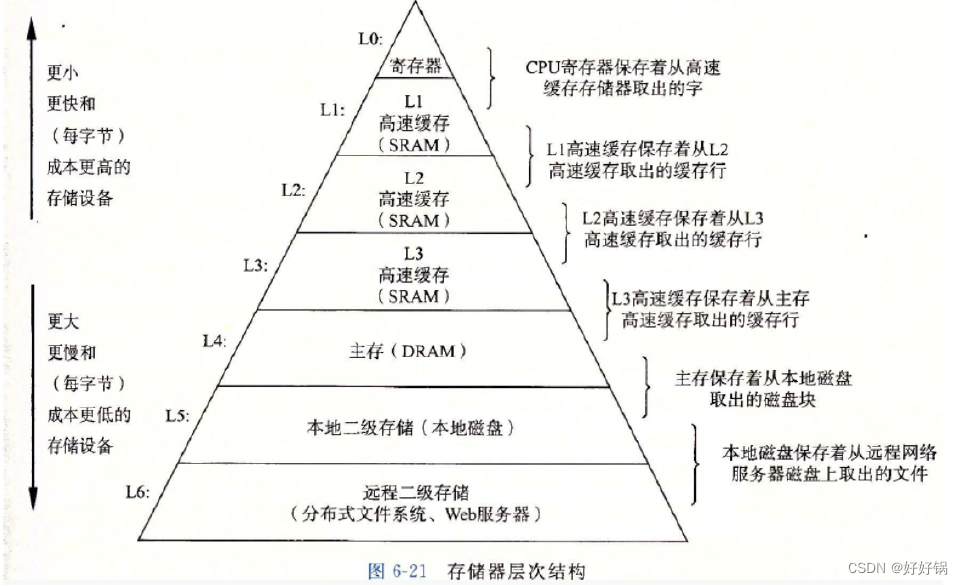
第五章:C语言数据结构与算法之双向带头循环链表
系列文章目录 文章目录系列文章目录前言一、哨兵位的头节点二、双向链表的结点三、接口函数的实现1、创建结点2、初始化3、尾插与尾删4、头插与头删5、打印6、查找7、随机插入与随机删除8、判空、长度与销毁四、顺序表和链表的对比1. 不同点2. 优缺点五、缓存命中1、缓存2、缓存…...
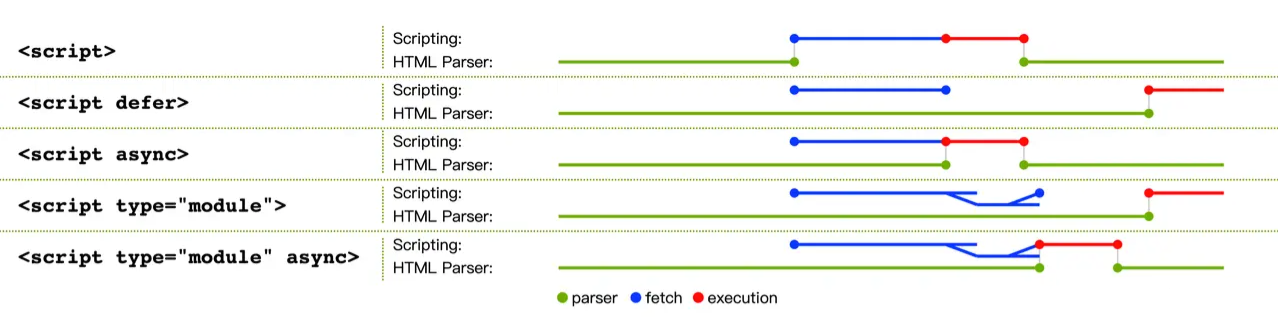
一文带你了解,前端模块化那些事儿
文章目录前端模块化省流:chatGPT 总结一、参考资料二、发展历史1.无模块化引出的问题:横向拓展2.IIFE3.Commonjs(cjs)4.AMD引出的问题:5.CMD6.UMD7.ESM往期精彩文章前端模块化 省流:chatGPT 总结 该文章主要讲述了前端模块化的发展历史和各个…...
大白话设计索引的时候,我们一般要考虑哪些因素呢?(中))
(六十五)大白话设计索引的时候,我们一般要考虑哪些因素呢?(中)
今天我们继续来说一下,在设计索引的时候要考虑哪些因素。之前已经说了,你设计的索引最好是让你的各个where、order by和group by后面跟的字段都是联合索引的最左侧开始的部分字段,这样他们都能用上索引。 但是在设计索引的时候还得考虑其他的…...

Spring事务管理
文章目录1 事务1.1 需求1.2 原因分析1.3 错误解决1.4 yml配置文件中开启事务管理日志1 事务 1.1 需求 当部门解散了不仅需要把部门信息删除了,还需要把该部门下的员工数据也删除了。可当在删除员工数据出现异常时,就不会执行删除员工操作,出…...
数字化工厂装配线生产管理看板系统
电力企业业务复杂,组织结构复杂,不同的业务数据,管理要求也不尽相同。生产管理看板系统针对制造企业的生产应用而开发,能够帮助企业建立一个规范准确即时的生产数据库。企业现状:1、计划不清晰:生产计划不能…...
vxe-grid 全局自定义filter过滤器,支持字典过滤
一、vxe-table的全局筛选器filters的实现 官网例子:https://vxetable.cn/#/table/renderer/filter 进入之后:我们可以参照例子自行实现,也可以下载它的源码,进行调整 下载好后并解压,用vscode将解压后的文件打开。全局…...
ECharts 环形图组件封装
一、ECharts引入1.安装echarts包npm install echarts --save2.引入echarts这里就演示全局引入了,挂载到vue全局,后面使用时,直接使用 $echartsimport * as echarts from echarts Vue.prototype.$echarts echarts二、写echarts组件这里演示环…...

c++ 怎么调用python 提供的函数接口
在 C 中调用 Python 函数有多种方法,以下是其中的两种常见方法:使用 Python/C APIPython 提供了 C/C API,可以通过该 API 在 C 中调用 Python 函数。使用这种方法,需要先将 Python 解释器嵌入到 C 代码中,然后可以通过…...
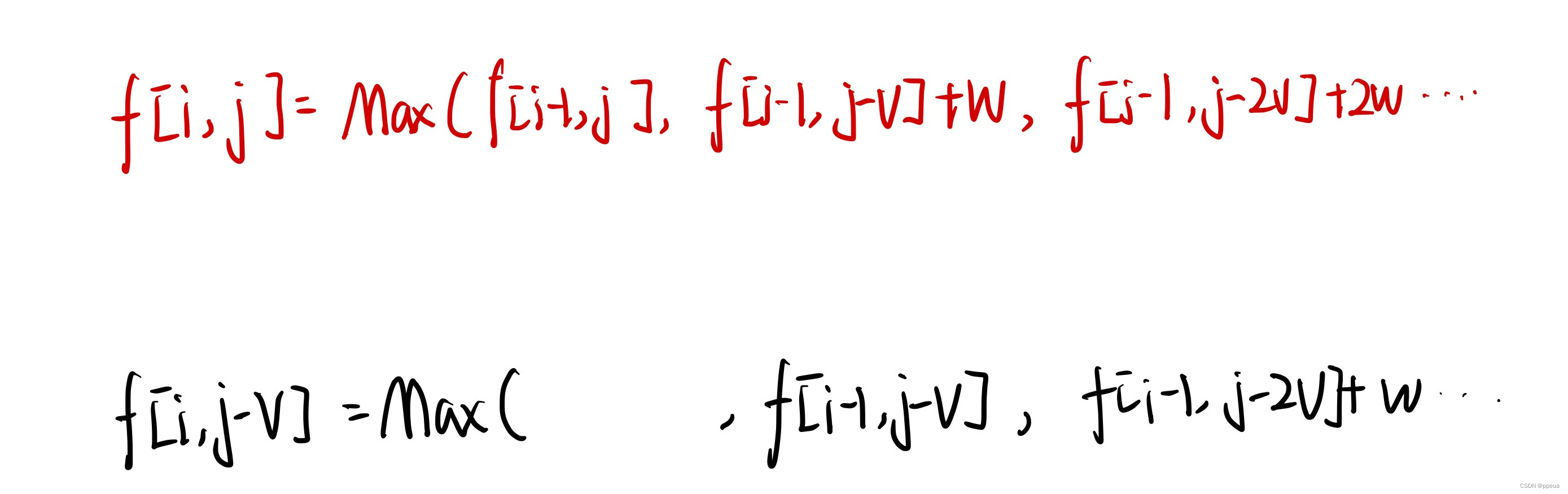
【动态规划】背包问题(01背包,完全背包)
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
记录 UE5 完全重新构建 UE C++项目
不知道搞了什么,C项目的实时代码编译罢工了,搞了半天都修不好,只能又重建了 UE5 版本为 v5.1.1 删除以下文件夹 /Binaries /Intermediate /SavedBinaries 文件夹是编译后的模块 Intermediate 文件夹里是中间层的C代码,完全由ue…...
java版云HIS系统源码 微服务架构支持VUE
云his系统源码 一个好的HIS系统,要具有开放性,便于扩展升级,增加新的功能模块,支撑好医院的业务的拓展,而且可以反过来给医院赋能,最终向更多的患者提供更好地服务。 私信了解更多! 本套基于…...

苹果内购支付检验错误码
21000 The request to the App Store didn’t use the HTTP POST request method. 对App Store的请求没有使用HTTP POST请求方法。 21001 The App Store no longer sends this status code. App Store不再发送此状态代码。 21002 The data in the receipt-data property…...

day27_css
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、CSS 零、 复习昨日 见代码 一 、引言 1.1CSS概念 层叠样式表(英文全称:Cascading Style Sheets)是一种用来表现HTML(标准通…...

智慧赋能,聚力开源——第四届OpenI/O 启智开发者大会开源治理专场顺利举办!
为汇聚国内外知名开源组织共同探讨中国开源生态建设及开源治理相关议题,推进产学研用开源合作,2月24日下午,第四届OpenI/O启智开发者大会在深圳人才研修院智汇中心举办以“构建开源联合体,共建开源生态”为主题的开源治理专场分论…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
