爬山算法教程(个人总结版)
背景与简介
爬山算法(Hill Climbing Algorithm)是一种用于解决优化问题的启发式搜索方法。它是一种局部搜索算法,通过不断尝试从当前解出发,在其邻域内寻找更优的解,直到无法找到更优解为止。该算法得名于其类似于登山的过程:从山脚出发,通过不断向高处前进,最终到达山顶(即局部最优解)。爬山算法在20世纪初被提出,是求解组合优化问题的重要方法,广泛应用于人工智能、运筹学、控制论和经济学等领域。
原理与步骤
原理
爬山算法的核心思想是从一个初始解开始,通过对解进行小幅度的调整,逐步找到一个更好的解,直到无法找到更优的解为止。算法的每一步都会选择邻域中最优的解,逐步提升解的质量。
同类算法对比
线性规划(Linear Programming)
线性规划是一种用于求解线性优化问题的数学方法。与爬山算法不同,线性规划可以保证找到全局最优解,但其应用范围仅限于线性问题。
优点:
- 能保证找到全局最优解。
- 对线性问题有很好的解决效果。
缺点:
- 只适用于线性问题,无法处理非线性问题。
- 复杂度较高,需要专门的数学基础和求解工具。
遗传算法(Genetic Algorithm)
遗传算法是一种基于自然选择和遗传变异的优化方法。与爬山算法相比,遗传算法更适合解决复杂的、多峰优化问题,但计算复杂度较高。
优点:
- 能处理复杂和多峰的优化问题。
- 具有较强的全局搜索能力。
缺点:
- 计算复杂度高,收敛速度慢。
- 参数选择较为复杂。
模拟退火(Simulated Annealing)
模拟退火是一种受物理退火过程启发的优化算法。它在搜索过程中允许接受较差的解,以避免陷入局部最优。与爬山算法相比,模拟退火能更有效地找到全局最优解,但计算时间可能更长。
优点:
- 能有效避免陷入局部最优。
- 适用于各种复杂的优化问题。
缺点:
- 计算时间较长。
- 参数选择和调优较为复杂。
步骤
- 初始解:随机选择或指定一个初始解。
- 评价函数:计算当前解的评价值。
- 邻域搜索:生成当前解的邻域解集(即通过小幅度改变当前解得到的一组新解)。
- 选择最优解:从邻域解集中选择评价值最优的解。
- 更新解:如果邻域解中的最优解比当前解更优,则将其作为新的当前解,并重复步骤2至4;否则,停止搜索。
伪代码
def hill_climbing(problem):current = problem.initial_state()while True:neighbors = problem.neighbors(current)if not neighbors:breakneighbor = max(neighbors, key=problem.value)if problem.value(neighbor) <= problem.value(current):breakcurrent = neighborreturn current
变种
- 随机爬山算法(Stochastic Hill Climbing):在选择邻域解时,随机选择一个比当前解好的解,而不是选择最优解。
- 首次爬山算法(First-Choice Hill Climbing):从邻域解中随机选择一个解,如果该解优于当前解,则立即采用。
- 模拟退火(Simulated Annealing):引入随机因素,允许在一定概率下接受较差的解,以避免陷入局部最优。
优缺点
优点
- 简单易用:算法结构简单,容易实现和理解。
- 高效:在解决一些特定问题时,爬山算法的计算效率很高。
缺点
- 局部最优问题:容易陷入局部最优解,无法保证找到全局最优解。
- 依赖初始解:最终解的质量很大程度上依赖于初始解的选择。
实际应用
函数优化
爬山算法可以用于求解各种函数的最优化问题。例如,在数学和工程中,常需要找到某个函数的最大值或最小值。通过爬山算法,可以逐步调整输入参数,找到使函数值最大的输入。
实例:函数优化 :
![]()
import randomdef objective_function(x):return -x**2 + 4*x + 6def hill_climbing():current_x = random.uniform(-10, 10) # 随机初始解step_size = 0.1 # 步长while True:neighbors = [current_x - step_size, current_x + step_size]next_x = max(neighbors, key=objective_function)if objective_function(next_x) <= objective_function(current_x):breakcurrent_x = next_xreturn current_xoptimal_x = hill_climbing()
print(f'Optimal x: {optimal_x}, Optimal value: {objective_function(optimal_x)}')
路径规划
在机器人和自动驾驶等领域,路径规划是一个重要的问题。爬山算法可以用于寻找从起点到终点的最短路径。
实例:路径规划 在一个网格图中寻找从起点到终点的最短路径。
class GridProblem:def __init__(self, grid, start, goal):self.grid = gridself.start = startself.goal = goaldef initial_state(self):return self.startdef neighbors(self, state):x, y = statepossible_moves = [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]return [move for move in possible_moves if self.is_valid(move)]def is_valid(self, state):x, y = statereturn 0 <= x < len(self.grid) and 0 <= y < len(self.grid[0]) and self.grid[x][y] == 0def value(self, state):return -abs(state[0] - self.goal[0]) - abs(state[1] - self.goal[1])grid = [[0, 0, 1, 0, 0],[0, 0, 1, 0, 0],[0, 0, 0, 0, 0],[0, 1, 1, 1, 0],[0, 0, 0, 0, 0]
]problem = GridProblem(grid, (0, 0), (4, 4))
optimal_state = hill_climbing(problem)
print(f'Optimal state: {optimal_state}')
超参数优化
在机器学习中,模型的性能很大程度上取决于超参数的选择。爬山算法可以用于调整模型的超参数,以提高模型的性能。
排程问题
在制造和生产中,排程问题涉及到资源的优化分配。爬山算法可以用于制定最优的生产计划和资源分配方案。
总结
爬山算法是一种简单且高效的局部搜索算法,适用于解决各种优化问题。尽管容易陷入局部最优,但通过改进和变种,可以在许多实际应用中获得满意的解。相比其他优化算法,爬山算法具有实现简单、高效的优点,但在应对复杂、多峰问题时可能表现不佳。掌握爬山算法及其变种,将为你在优化和搜索领域提供有力的工具。
相关文章:

爬山算法教程(个人总结版)
背景与简介 爬山算法(Hill Climbing Algorithm)是一种用于解决优化问题的启发式搜索方法。它是一种局部搜索算法,通过不断尝试从当前解出发,在其邻域内寻找更优的解,直到无法找到更优解为止。该算法得名于其类似于登山…...

水电表远程抄表:智能化时代的能源管理新方式
1.行业背景与界定 水电表远程抄表,是随着物联网技术发展,完成的一种新型的能源计量管理方式。主要是通过无线传输技术,如GPRS、NB-IoT、LoRa等,将水电表的信息实时传输到云服务器,进而取代了传统人工当场抄水表。这种…...
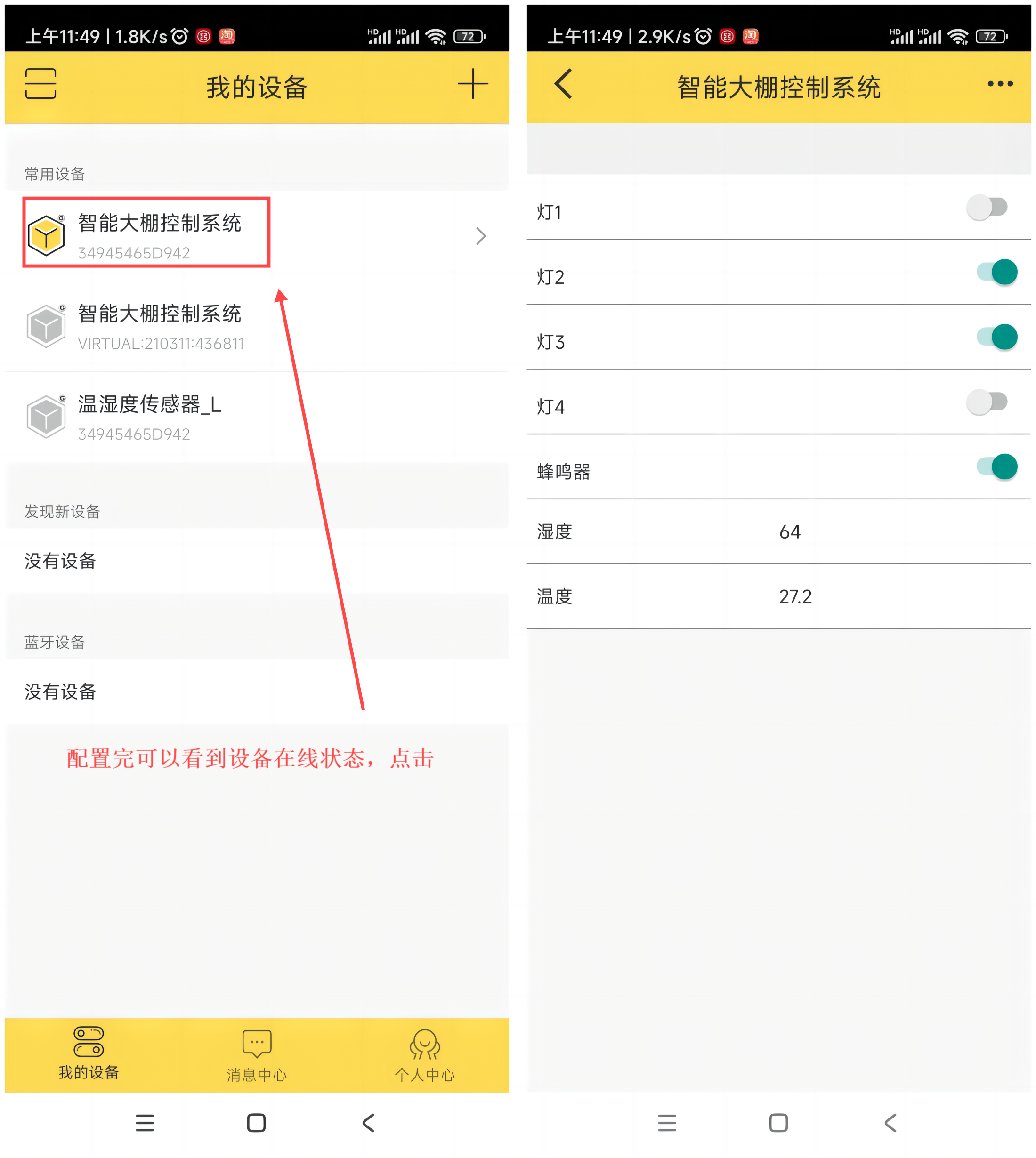
物联网应用开发--STM32与机智云通信(ESP8266 Wi-Fi+手机APP+LED+蜂鸣器+SHT20温湿度传感器)
实现目标 1、熟悉机智云平台,会下载APP 2、熟悉新云平台创建产品,项目虚拟调试 3、掌握云平台生成MCU代码,并移植。机智云透传固件的下载 4、具体目标:(1)注册机智云平台;(2&…...
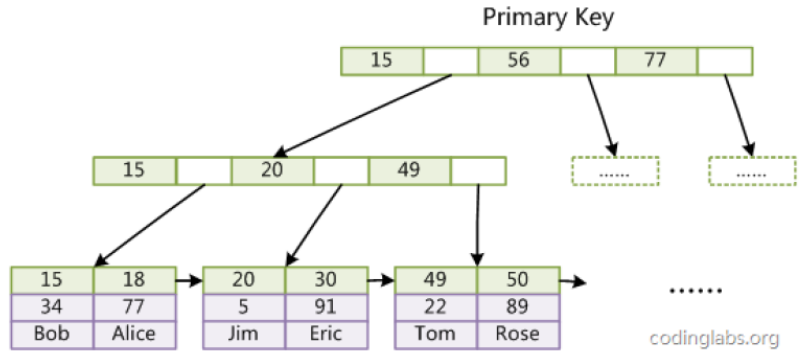
【高阶数据结构(七)】B+树, 索引原理讲解
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:高阶数据结构专栏⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习更多数据结构 🔝🔝 高阶数据结构 1. 前言2. B树讲解…...
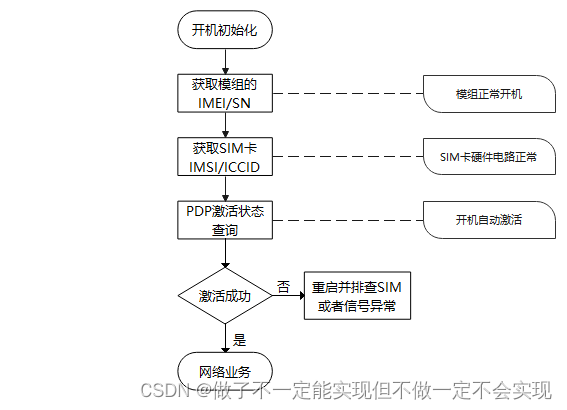
ML307R OpenCPU 网络初始化流程介绍
一、网络初始化流程 二、函数介绍 三、示例代码 四、代码下载地址 一、网络初始化流程 模组的IMEI/SN获取接口可在include\cmiot\cm_sys.h中查看,SIM卡IMSI/ICCID获取接口可以在include\cmiot\cm_sim.h中查看,PDP激活状态查询可以在include\cmiot\cm_modem.h中查看 二、函…...

分享:怎么才能保证大数据查询的准确性?
随着大数据应用到金融风控领域,大数据越来越重要了,很多朋友在查大数据的时候都会遇到一个问题,那就是自己查询的大数据什么信息都没有,要么就是很少,这是什么原因呢?要怎么才能保证大数据查询的准确性呢?下面小编就…...
AI Agent教育行业落地案例
【AI赋能教育】揭秘Duolingo背后的AI Agent,让学习更高效、更有趣! ©作者|Blaze 来源|神州问学 引言 随着科技的迅猛发展,人工智能技术已经逐步渗透到我们生活的各个方面。而随着AI技术的广泛应用,教育培训正引领着一场新的…...

Flutter 中的 LimitedBox 小部件:全面指南
Flutter 中的 LimitedBox 小部件:全面指南 Flutter 是一个功能强大的 UI 框架,它提供了大量的小部件来帮助开发者构建美观且响应式的用户界面。在 Flutter 的布局小部件中,LimitedBox 是一个不太常见但非常有用的组件,它可以用来…...

OrangePi AIpro初体验,码农的第一台个人AI云电脑
介绍 香橙派联合华为精心打造,建设人工智能新生态 官网地址:Orange Pi AIpro Orange Pi官网-香橙派 Orange Pi论坛:Orange Pi论坛 昇腾社区:为开发者免费提供数百个代码参考样例昇腾社区-官网丨昇腾万里 让智能无所不及 学习…...
剪画小程序:”霸屏各大平台“的黏土滤镜是怎么制作的呢?
最近,网上出现大量“黏土”风格的人物照片。尤其是在社交平台,这类型的分享数量急剧上升。 这是马斯克开车的样子 还有这张是周杰伦七里香的专辑图片 一张照片,十几秒钟,就能还原出你在黏土世界的样子。 以上这些照片是用-【剪画…...
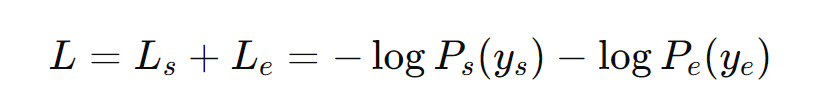
图解 BERT 模型
节前,我们星球组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、参加社招和校招面试的同学. 针对算法岗技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备、面试常考点分享等热门话题进行了深入的讨论。 汇总合集&…...

关于软件设计模式的理解
系列文章 关于时间复杂度o(1), o(n), o(logn), o(nlogn)的理解 关于HashMap的哈希碰撞、拉链法和key的哈希函数设计 关于JVM内存模型和堆内存模型的理解 关于代理模式的理解 关于Mysql基本概念的理解 关于软件设计模式的理解 文章目录 前言一、软件设计模式遵循的六大原则…...

Java开发官方文档
Spring中文网 Spring Cloud中文网 Hutool工具类 Ant Design官方文档 遇见狂神说学习文档 若依后台管理系统测试环境 FineBI官方文档 vscode教程 新一代微服务全家桶AlibabaCloudSpringCloud实战 分布式任务调度平台XXL-JOB...

AI大模型探索之路-实战篇9:探究Agent智能数据分析平台的架构与功能
系列篇章💥 AI大模型探索之路-实战篇4:深入DB-GPT数据应用开发框架调研 AI大模型探索之路-实战篇5:探索Open Interpreter开放代码解释器调研 AI大模型探索之路-实战篇6:掌握Function Calling的详细流程 AI大模型探索之路-实战篇7…...
 集成paimon0.9)
本地spark3.5(不整合hive) 集成paimon0.9
spark官网下载集成hadoop的spark包: spark-3.5.1-bin-hadoop3.... 解压后 环境变量配置 SPARK_HOME spark-defaults.conf 中增加一行配置(避免启动spark-sql报错hive元数据连不上): spark.sql.catalogImplementationhive 打开paimon官网: https://paimon.apache.org/docs/mas…...
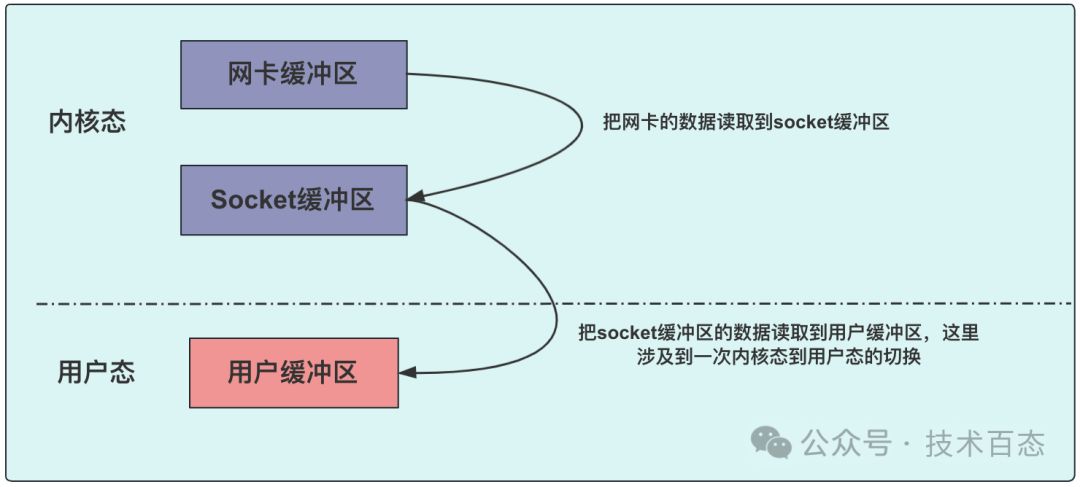
Linux IO模型深度解析与实战应用
linux的5种IO模型 一、这里IO是什么 操作系统设有用户态与内核态,确保系统安全。应用程序默认在用户态运行,而执行如IO操作等底层任务时,需切换至内核态以高效执行。 服务器从网络接收的大致流程如下: 1、数据通过计算机网络来到了网卡 2、把网卡的数据读取到 socket 缓…...

软件系统开发标准流程文档(Word原件)
目的:规范系统开发流程,提高系统开发效率。 立项申请需求分析方案设计方案评审开发调整测试阶段系统培训试运行测试验收投入使用 所有文档过去进主页获取。 软件项目相关全套精华资料包获取方式①:点我获取 获取方式②:本文末个人…...
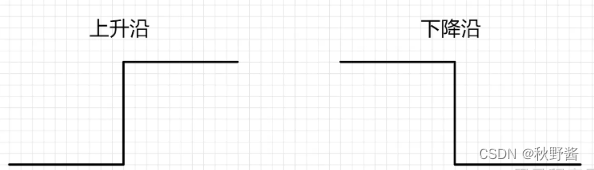
嵌入式进阶——外部中断(EXTI)
🎬 秋野酱:《个人主页》 🔥 个人专栏:《Java专栏》《Python专栏》 ⛺️心若有所向往,何惧道阻且长 文章目录 STC8H中断外部中断外部中断编写配置外部中断调用中断触发函数 外部中断测试测试外部中断0测试外部中断2、3或者4 PCB中断设计 STC8…...
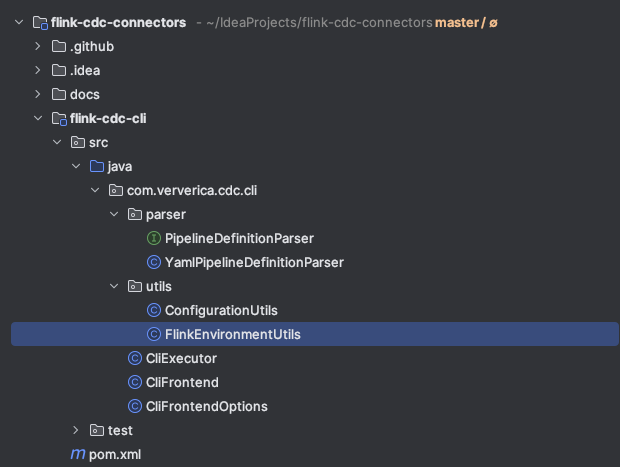
flinkcdc 3.0 源码学习之客户端flink-cdc-cli模块
注意 : 本文章是基于flinkcdc 3.0 版本写的 我们在前面的文章已经提到过,flinkcdc3.0版本分为4层,API接口层,Connect链接层,Composer同步任务构建层,Runtime运行时层,这篇文章会对API接口层进行一个探索.探索一下flink-cdc-cli模块,看看是如何将一个yaml配置文件转换成一个任务…...
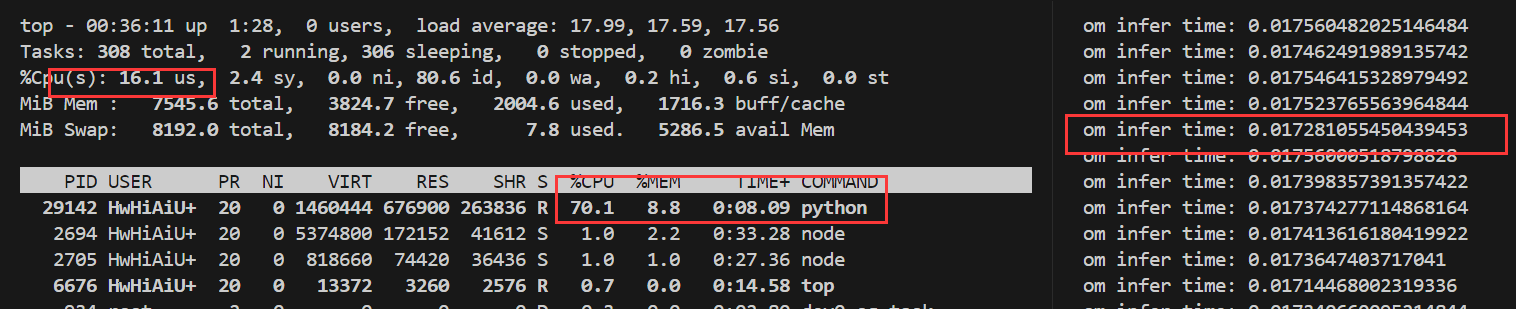
香橙派 AIpro开发体验:使用YOLOV8对USB摄像头画面进行目标检测
香橙派 AIpro开发体验:使用YOLOV8对USB摄像头画面进行目标检测 前言一、香橙派AIpro硬件准备二、连接香橙派AIpro1. 通过网线连接路由器和香橙派AIpro2. 通过wifi连接香橙派AIpro3. 使用vscode 通过ssh连接香橙派AIpro 三、USB摄像头测试1. 配置ipynb远程开发环境1.…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
