Kalman Filter in SLAM (1) ——Data Fusion and Kalman Filter(数据融合和卡尔曼滤波)

文章目录
- 0. 参考资料
- 1. Intro Example 例子引入
- 1.1. 测量硬币直径
- 1.2. 思考
- 2. Data Fusion 数据融合
- 2.1. 数据融合在做什么?
- 2.2. 数据融合的前提——不确定度
- 2.3. 数据融合的结果——统计意义下的最优估计
- 3. State Space Representation 状态空间表达式
- 3.1. 状态方程
- 3.2. 观测方程
- 3.3. 系统状态空间方程举例
- 4. Kalman Filter 卡尔曼滤波
- 4.1. Kalman Filter 在做什么?
- 4.2. Kalman Filter 的思路
- 4.3. Kalman Gain
- 4.4. Kalman Filter 五大公式总结
0. 参考资料
【卡尔曼滤波器】_Kalman Filter_全网最详细数学推导
1. Intro Example 例子引入
1.1. 测量硬币直径
给你如下不同的传感器,如何得到硬币的直径?
- Test 1:只给你一个米尺。
Answer 1:用米尺测两次硬币直径,取平均值。
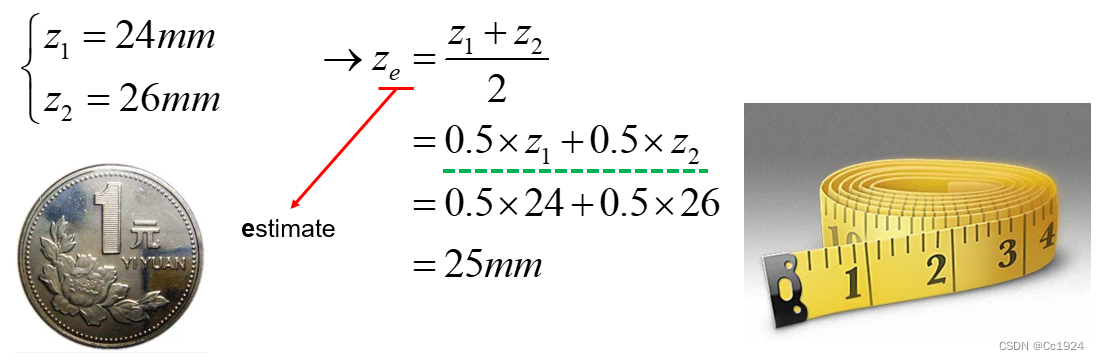
-
Test 2:给你两个刻度分辨率不同的米尺。
Answer 2:分别用两个米尺测量一次,此时还能取平均值吗?

-
Test 3:给你一个米尺和一个千分尺。
Answer 3:分别用米尺和千分尺各测量一次,此时还能取平均值吗?

1.2. 思考
显然随着传感器精度的不同,我们使用不同的传感器测量的结果不能再简单的取平均值了,因为在不考虑系统误差的情况下,千分尺的测量结果显然要比米尺的测量结果更准确。
那么如何从不同传感器的测量结果中,得到我们对硬币直径的最优估计?这就需要后面数据融合的方法!
2. Data Fusion 数据融合
2.1. 数据融合在做什么?
使用不同的传感器,获得对系统状态的最优估计。
比如上述例子中,使用不同的传感器测量硬币直径,最后需要给出对硬币直径的最优估计。

2.2. 数据融合的前提——不确定度
没有完全准确的传感器,也不存在完全准确的测量过程。也就是说,每次测量都是存在不确定度的,只不过是在不考虑系统误差的情况下,传感器精度越高,其测量的不确定度就越小。比如上述例子中,千分尺的测量不确定度就要远小于米尺的测量不确定度。
不确定度在统计学中就是标注差、方差、协方差矩阵的概念。显然在前面的例子中,在对不同传感器测量的结果进行加权平均的时候,我们应该考虑不同传感器的不确定度,也就是不确定度越小的传感器,其测量值所占的权重应该越大,因为它更准确。

2.3. 数据融合的结果——统计意义下的最优估计
每次测量都是有不确定度的,所以从统计意义上讲我们的测量值是一个随机变量,而最终我们对系统状态的估计值也是一个随机变量。那么最优的数据融合结果应该有最小的方差,对于多维随机变量来说就是拥有最小的协方差矩阵的迹。
所以下面我们推导前面的不同传感器测量的结果进行加权平均的时候,目的就是让最后加权平均的结果有最小的方差。

推导结果如上图所示,其中两侧测量是独立的,所以根据方差的性质可以展开成两部分。然后最终的目的是求解kkk让方差最小,所以我们就是对kkk求导,导数为0的点就是极值点。
最终的结果也是容易解释的,分成两种情况:
- σ12\sigma_1^2σ12非常大,kkk趋向1,融合结果趋向z2z_2z2。这个显然是对的,因为测量1的方差很大,也就是它的测量结果更不准确,所以我们倾向于相信测量2的结果。
- σ22\sigma_2^2σ22非常大,kkk趋向0,融合结果趋向z1z_1z1。分析同上。
利用我们上面推导得到的公式,带到前面米尺和千分尺测量硬币直径的例子中,看一下最终融合的结果,可以发现结果非常靠近千分尺的结果,这个也是我们想要的。

3. State Space Representation 状态空间表达式
在机器人状态估计问题中,并不是简单的两个传感器测量状态然后融合结果的过程,而是通常会对系统的运动过程做一个建模,根据这个建模的运动过程我们就可以预测系统的状态。当有新的传感器测量之后,再根据测量结果更新我们对系统状态的预测值,从而达到更优的系统状态估计。
上述过程其实就是系统的状态空间表达式,在Kalman Fiter中分为状态方程和观测方程两个部分:
3.1. 状态方程
对系统的物理模型进行数学建模,比如SLAM中假设机器人在做匀速匀速或者加速运动,那么建立的数学模型就分别是匀速运动模型和加速运动模型。
总而言之,状态方程是我们算出来的,或者推导出来的。知道了系统上一时刻的状态,利用状态方程,我们就可以计算得到当前时刻的系统状态,这就是对系统状态的预测。
另外一个值得注意的问题是,和 数据融合 章节中我们提到的一样,不管是测量值还是我们这里的数学建模,都是有不确定性的,比如这里我们建立的数学模型可能不准确,所以状态方程是有噪声的。在Kalman Filter中,假设噪声符合高斯分布,这是后面推导Kalman Gain的必要前提条件。

3.2. 观测方程
这个和前面测量硬币直径是一样的,就是我们对系统状态进行的观测。但是在SLAM中可能没有前面那么直接,而是有一个观测模型在里面。比如VIO中我们要估计系统的6DOF位姿,但是其实我们从相机中直接拿到的是特征点观测的像素值,而不是直接对系统6DOF的观测值。但是这个观测值和系统的6DOF状态是有关系的,也就是相机的投影模型,在这个投影模型中,就把实际的 观测像素值 和 系统6DOF状态值 关联到一起了,这个关联的关系就是观测模型。
总而言之,观测方程尽管没有直接对要估计的系统状态进行测量,但是它通过观测模型间接对系统状态进行了测量,因此它最终还是对系统状态的测量。
同理,观测也是有噪声的,比如相机观测的特征点的位置可能并不是很准确,相机的投影模型可能也不是很准确,所以这里也要加入高斯噪声,注意这里也必须是高斯噪声,因为这是后面推导Kalman Gain的前提条件。

3.3. 系统状态空间方程举例
假设有个小车,上面有一个单线激光发射器可以测量它离起始点的距离,有一个轮速计可以测量轮子的速度。现在我们的目的就是估计这个小车的状态,那么系统状态空间方程可以建立如下:

注意:上述建立状态空间方程的过程中,把轮速计的测量加到了状态方程中,把激光的测量加到了观测方程中。按理说他俩不都是观测吗?为什么要把轮速计加到状态方程中呢?
其实把轮速计加到观测方程中和加到状态方程中本质是一样的,加到状态方程中我们就把噪声加到了轮速的地方,这个时候它就是作为状态方程的输入量uuu。如果把它加到观测方程中,那么状态方程中uuu就是0了,系统就是靠上次的速度递推这次的状态,然后轮速计在观测方程中对速度进行约束。可以发现其实这两种建模方式都是本质是一样的,只不过是在数学表达上不太一样。
4. Kalman Filter 卡尔曼滤波
4.1. Kalman Filter 在做什么?
Kalman Filter(卡尔曼滤波),名字叫做滤波,但是更准确的说它不是一个滤波器,而是一个状态估计器。
它的目的就是利用系统的状态方程和观测方程,得到对系统状态在统计意义下的最优估计。

注意:Kalman Filter的两大前提:
- 状态方程和观测方程都是线性的,也就是要有系数矩阵AAA和HHH;
- 状态方程和观测方程的噪声都是高斯噪声。
注意这两个条件是卡尔曼滤波应用的前提条件,因为只有在这两个前提条件下,推导得到的 Kalman Gain 才能让融合的结果在统计意义上是最优的。
4.2. Kalman Filter 的思路
既然是用状态方程和观测方程融合,那么就写出来他们对系统状态的估计结果,然后像测量硬币直径一样对两个结果进行数据融合就可以了。如下所示:

注意:
- 用状态方程得到的结果称为预测值,其中在计算的过程中我们把过程噪声www认为是0,因为它是0均值的高斯分布 。这个噪声这次到底是多少我们没办法知道,因为它是随机的高斯噪声。如果知道了我们就不用做Kalman Filter了,直接把噪声的值带入状态空间方程中,就得到系统的真值状态了。正是因为我们不知道每一次噪声到底是多少,才需要用Kalman Filter来估计系统的状态。所以我们在计算的时候,只能把噪声值设置成它的均值,也就是0。当前如果噪声的均值不是0,那么是多少这里带入多少就行了,总之带入的就是噪声www的均值。观测方程中对噪声的处理同理。
- 观测方程中,由于它不是直接对系统状态进行观测,而是有一个观测模型。也就是有一个系数矩阵HHH在系统状态变量和观测变量之间做了映射,因此我们想要从传感器测量中得到直接对状态的观测,需要求伪逆。这个地方只是为了后续推导的理解方便,最终Kalman Filter的结果中是不存在这个求伪逆的过程的。
套用数据融合的思路,我们只需要对状态预测值和状态观测值做加权就可以了,如下所示:

对前面的加权平均的式子进行进一步推导,消掉其中求HHH的伪逆的过程,可以得到如下结果,其中的KKK就是大名鼎鼎的 Kalman Gain:

在套用数据融合中的思路,我们最终的目的就是找到一个合适的权重系数,让最终的加权平均的结果有最小的方差,对于多维随机变量来说就是有最小的协方差矩阵的迹。如下所示:

注意:
- 其中预测状态的协方差P^k\hat{P}_kP^k是通过系统的状态方程计算出来的。而观测方程的协方差因为现在我们没有从观测空间转到状态空间,也就是没有求伪逆,所以直接就是观测的协方差RRR。
4.3. Kalman Gain
这个部分非常复杂,详细的推导过程可以参照B站视频:【卡尔曼滤波器】3_卡尔曼增益超详细数学推导 ~全网最完整

或者我的手写笔记:Kalman Filter in SLAM (1.5) ——Derivation of Kalman Gain and Covariance Matrix (卡尔曼增益和协方差矩阵推导)
这里直接给出结果:

4.4. Kalman Filter 五大公式总结
- 状态方程做预测:根据上一时刻的状态和系统状态空间方程,对当前时刻的状态做预测,同时会更新当前预测的状态的协方差矩阵:

- 观测方程做更新:首先计算 Kalman Gain,然后把它当做权重融合预测状态和观测值,得到系统的最优估计。可以看到,这里预测值是系统状态,观测值是传感器直接的观测量,所以 Kalman Gain 是有量纲的,而且它的量纲和H−1H^{-1}H−1量纲是一样的。

相关文章:
Kalman Filter in SLAM (1) ——Data Fusion and Kalman Filter(数据融合和卡尔曼滤波)
文章目录0. 参考资料1. Intro Example 例子引入1.1. 测量硬币直径1.2. 思考2. Data Fusion 数据融合2.1. 数据融合在做什么?2.2. 数据融合的前提——不确定度2.3. 数据融合的结果——统计意义下的最优估计3. State Space Representation 状态空间表达式3.1. 状态方程…...

黑马程序最后
这里写自定义目录标题内建stl常用算法adjacent_findbinary_searchcountcount if常用排序算法常用拷贝和替换replace常用算术生成算法常用集合算法https://gitee.com/jiangjiandong/Cpp-0-1-Resource/blob/master/%E7%AC%AC5%E9%98%B6%E6%AE%B5-C%E6%8F%90%E9%AB%98%E7%BC%96%E7…...

u盘系统文件删除后的五种恢复方法
U盘是我们日常生活中使用较为普遍的移动存储设备,由于其便携性和易用性广受人们的欢迎。然而,在我们使用U盘的过程中,经常会出现误删文件的情况,例如本来要作为启动盘的u盘,误删里面的系统文件怎么办?当U盘…...

【玩转c++】List讲解和模拟底层实现
本期主题:list的讲解和模拟实现博客主页:小峰同学分享小编的在Linux中学习到的知识和遇到的问题小编的能力有限,出现错误希望大家不吝赐1.list的介绍和使用1.1.list的介绍1.list是可以在常数范围内在任意位置进行插入和删除的序列式容器&…...

【Python】特征编码
特征编码1. 独热编码(离散变量编码) sklearn.preprocessing.OneHotEncoder1.1 原理 & 过程1.2 封装函数2. 连续变量分箱(连续变量编码) sklearn.preprocessing.KBinsDiscretizer2.1 原理2.2 等宽分箱 KBinsDiscretizer(strategyuniform)2.3 等频分箱 KBinsDiscretizer(stra…...
前端开发者必备的Nginx知识
nginx在应用程序中的作用 解决跨域请求过滤配置gzip负载均衡静态资源服务器…nginx是一个高性能的HTTP和反向代理服务器,也是一个通用的TCP/UDP代理服务器,最初由俄罗斯人Igor Sysoev编写。 nginx现在几乎是众多大型网站的必用技术,大多数情…...
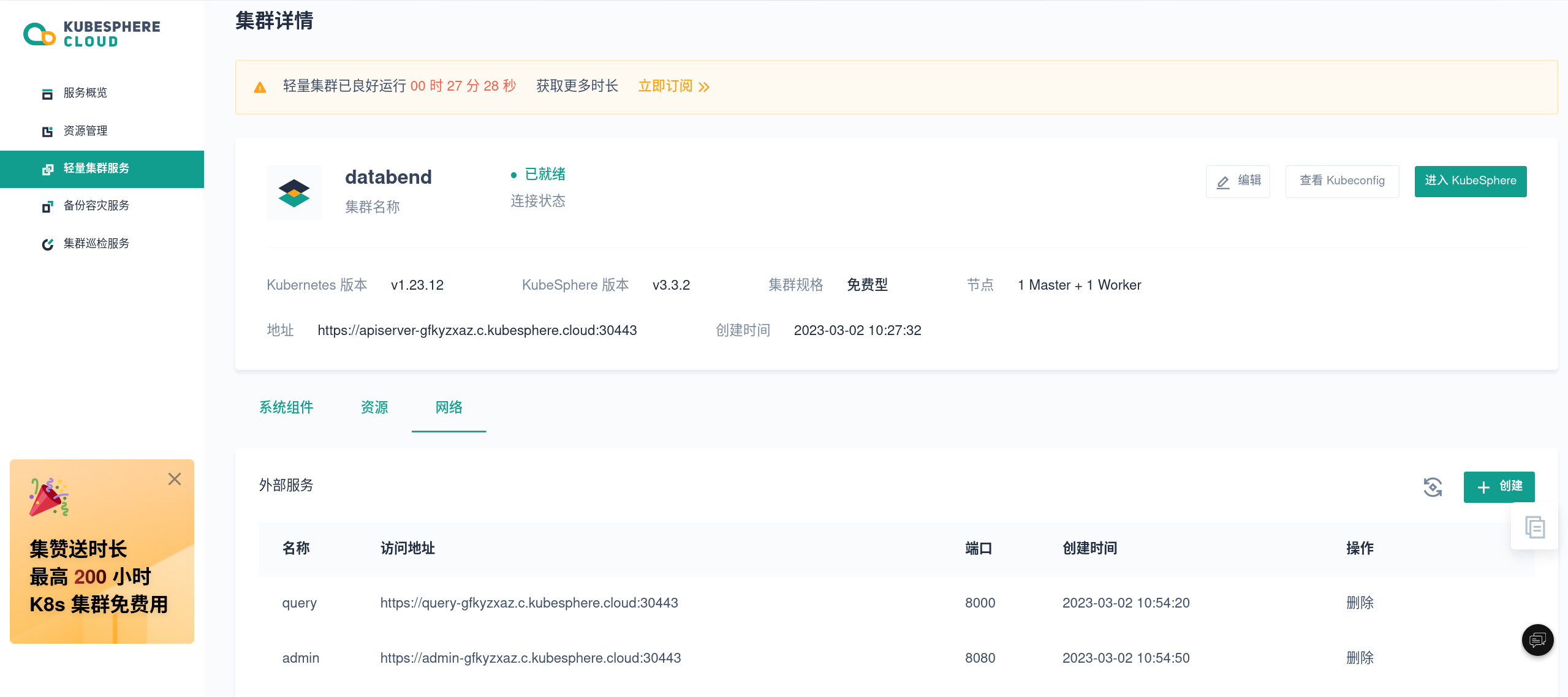
在 KubeSphere 中开启新一代云原生数仓 Databend
作者:尚卓燃(https://github.com/PsiACE),Databend 研发工程师,Apache OpenDAL (Incubating) PPMC。 前言 Databend 是一款完全面向云对象存储的新一代云原生数据仓库,专为弹性和高效设计,为您…...
【独家】)
华为OD机试 - 最优资源分配(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:最优资源…...

求数组的中心索引
给你一个整数数组 nums ,请计算数组的 中心下标 。 数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。 如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点…...
Ubuntu 搭建NextCloud私有云盘【内网穿透远程访问】
文章目录1.前言2.本地软件安装2.1 nextcloud安装2.2 cpolar安装3.本地网页发布3.1 Cpolar云端设置3.2 Cpolar本地设置4.公网访问测试5. 结语1.前言 对于爱好折腾的电脑爱好者来说,Linux是绕不开的、必须认识的系统(大部分服务器都是采用Linux操作系统&a…...
如何使用vue创建一个完整的前端项目
搭建Vue项目的完整流程可以分为以下几个步骤:安装Node.js和npm:Vue.js是基于Node.js开发的,因此在开始搭建Vue项目之前,需要先安装Node.js和npm(Node.js的包管理器)。可以从官网下载Node.js安装包并安装。安…...
http组成及状态及参数传递
http组成及状态及参数传递 早期的网页都是通过后端渲染来完成的:服务器端渲染(SSR,server side render): 客户端发出请求 -> 服务端接收请求并返回相应HTML文档 -> 页面刷新,客户端加载新的HTML文档&…...

USART_GetITStatus与 USART_GetFlagStatus的区别
文章目录共同点不同点USART_GetITStatus函数详解USART_GetFlagStatus函数共同点 都能访问串口的SR寄存器 不同点 USART_GetFlagStatus(USART_TypeDef USARTx, uint16_t USART_FLAG):* 该函数只判断标志位(访问串口的SR寄存器)。在没有使能…...
Java 系列之 Springboot
系列文章目录 文章目录系列文章目录前言一、Springboot 简介?1.1 什么是启动器?1.2 Springboot 优点1.3 Springboot 核心二、搭建方式2.1 搭建方式一2.2 搭建方式二2.3 搭建方式三三、启动原理3.1 初始化SrpingApplication对象3.2 执行run()方法1. 加载监…...

乐山持点科技:抖客推广准入及准出管理规则
抖音小店平台新增《抖客推广准入及准出管理规则》,本次抖音规则具体如下:第一章 概述1.1 目的及依据为维护精选联盟平台经营秩序,保障精选联盟抖客、商家、消费者等各方的合法权益;根据《巨量百应平台服务协议》、《“精选联盟”服务协议(推广…...

Steam流
Steam流 Stream 流是什么,为什么要用它? Stream是 Java8 新引入的一个包( java.util.stream),它让我们能用声明式的方式处理数据(集合、数组等)。Stream流式处理相较于传统方法简洁高效&#…...
Nuxt实战教程基础-Day01
Nuxt实战教程基础-Day01Nuxt是什么?Nuxt.js框架是如何运作的?Nuxt特性流程图服务端渲染(通过 SSR)单页应用程序 (SPA)静态化 (预渲染)Nuxt优缺点优点缺点安装运行项目总结前言:本教程基于Nuxt2,作为教程的第一天,我们先…...
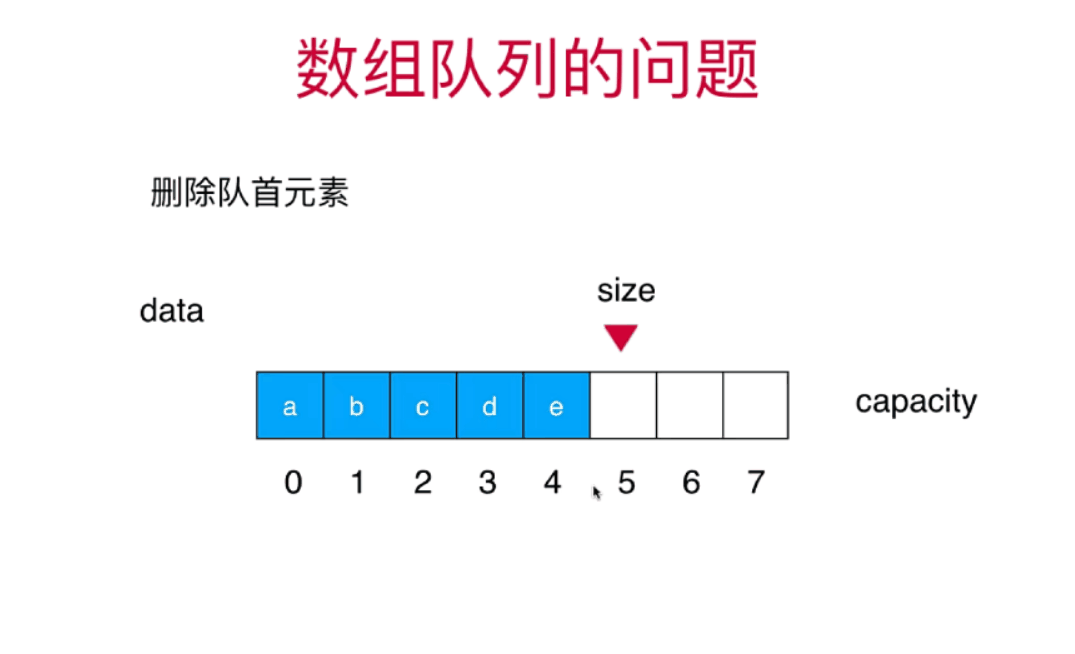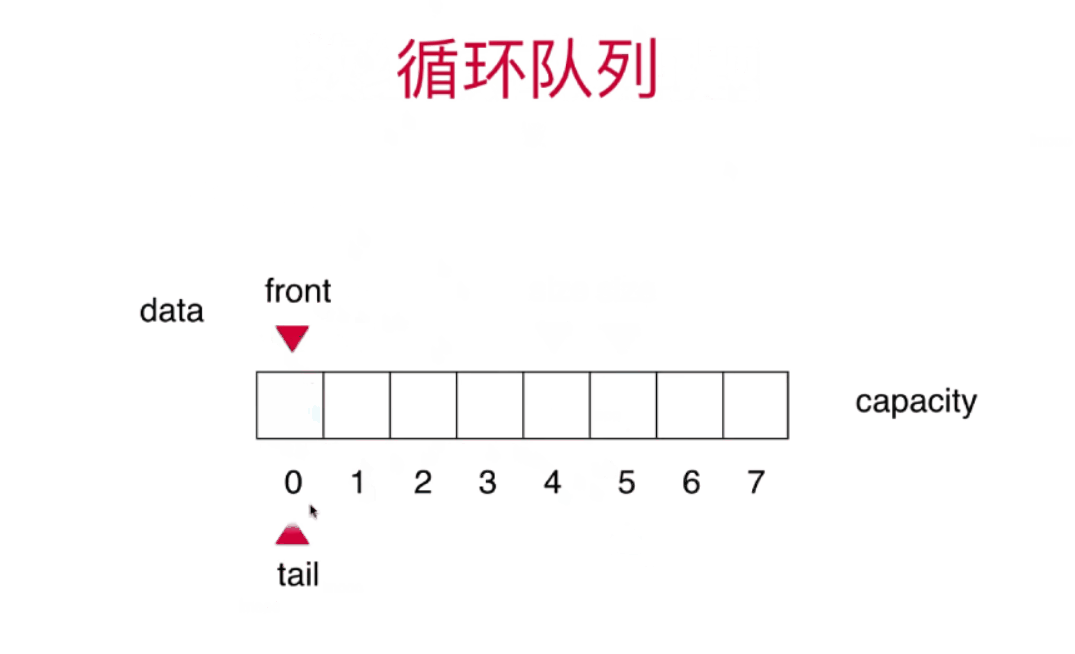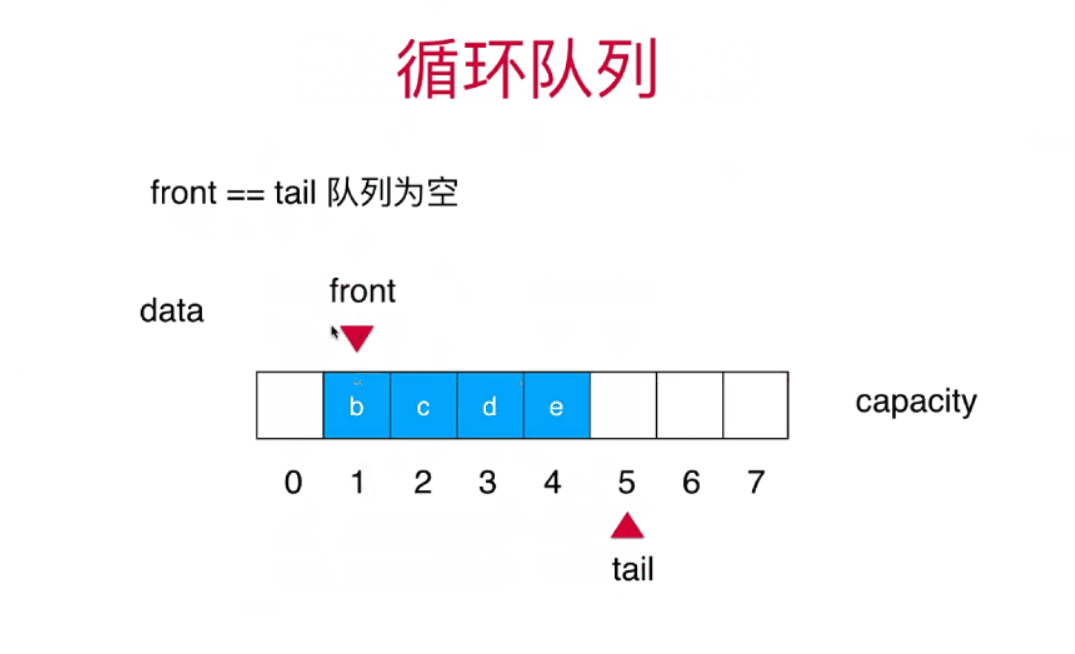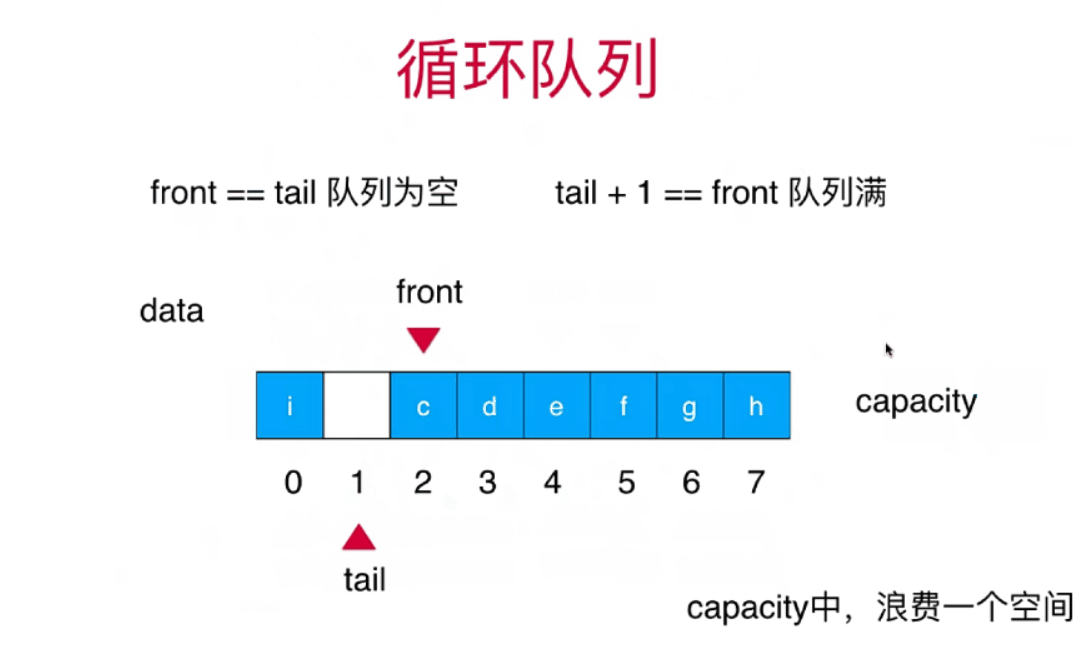
栈和队列详细讲解+算法动画
栈和队列 栈stack 栈也是一种线性结构相比数组,栈对应的操作数数组的子集只能从一端添加元素,也只能从一端取出元素这一端称为栈顶 栈是一种后进先出的数据结构Last in Firt out(LIFO)在计算机的世界里,栈拥有者不可思议的作用 栈的应用 …...
【Unity3D小技巧】Unity3D中判断Animation以及Animator动画播放结束,以及动画播放结束之后执行函数
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址我的个人博客 大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 在日常开发中,可能会遇到要判断Animation或者Anima…...

【1】熟悉刷题平台操作
TestBench使用 与quartus中testbench的写法有些许。或者说这是平台特有的特性!! 1 平台使用谨记 (1)必须删除:若设计为组合逻辑,需将自动生成的clk删除 若不删除,会提示运行超时错误。 &#…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

Android Framework预装traceroute执行文件到system/bin下
文章目录 Android SDK中寻找traceroute代码内置traceroute到SDK中traceroute参数说明-I 参数(使用 ICMP Echo 请求)-T 参数(使用 TCP SYN 包) 相关文章 Android SDK中寻找traceroute代码 设备使用的是Android 11,在/s…...

Gitlab + Jenkins 实现 CICD
CICD 是持续集成(Continuous Integration, CI)和持续交付/部署(Continuous Delivery/Deployment, CD)的缩写,是现代软件开发中的一种自动化流程实践。下面介绍 Web 项目如何在代码提交到 Gitlab 后,自动发布…...

【Ragflow】26.RagflowPlus(v0.4.0):完善解析逻辑/文档撰写模式全新升级
概述 在历经半个月的间歇性开发后,RagflowPlus再次迎来一轮升级,正式发布v0.4.0。 开源地址:https://github.com/zstar1003/ragflow-plus 更新方法 下载仓库最新代码: git clone https://github.com/zstar1003/ragflow-plus.…...

NLP常用工具包
✨做一次按NLP项目常见工具的使用拆解 1. tokenizer from torchtext.data.utils import get_tokenizertokenizer get_tokenizer(basic_english) text_sample "Were going on an adventure! The weather is really nice today." tokens tokenizer(text_sample) p…...
