查找、排序、二叉树的算法,统统记录于此。
文章目录
- 一、查找
- 1. 无序表的顺序查找
- 2. 折半查找
- 3. 分块查找
- 4. 二叉排序树BST
- 5. 哈希表查找
- 二、排序
- 1. 不带哨兵的直接插入排序
- 2. 带哨兵的直接插入排序
- 3. 带哨兵、折半查找的直接插入排序
- 4. 希尔排序
- 5. 冒泡排序
- 6. 快速排序
- 7. 选择排序
- 8. 堆排序
- 9. 归并排序
- 二叉树
- 1. 递归先序遍历
- 2. 非递归先序遍历
- 3. 递归中序遍历
- 4. 非递归中序遍历
- 5. 递归后序遍历
- 6. 非递归后序遍历
- 7. 广度遍历二叉树
- 8. 深度遍历
一、查找
1. 无序表的顺序查找
把待查关键字key存入表头(哨兵),从后向前逐个比较,可免去查找过程中每一步都要检测是否查找完毕,加快速度。
// 下标从1开始,头节点为空
public static int sentrySearch(int[] arr, int target){arr[0] = target;int index = arr.length-1;while(arr[index] != target){--index;}if(index == 0) return -1;return index;
}
- 空间复杂度:O(1)
- 时间复杂度:O(n)
- 平均查找长度:ASL =(n+1)/ 2
2. 折半查找
首先将给定值key与表中中间位置的元素比较,若相等则查找成功,返回该元素的存储位置;若不等则所需查找的元素只能在中间元素以外的前半部分或后半部分。
public static int Sort(int[] nums, int target){int low = 0;int high = nums.length;while(low < high){mid = (low + high) / 2;if(target == nums[mid]) return mid;if(target < nums[mid]) high = mid-1;if(target > nums[mid]) low = mid+1;}return -1
}
- 空间复杂度:O(1)
- 时间复杂度:O(log2log_2log2n)
- 平均查找长度:ASL = log2log_2log2(n+1)
3. 分块查找
分块查找又称索引顺序查找,它是顺序查找的一种改进方法:将n个数据元素“按块有序”划分为m块(m<=n)。每一块中的数据元素不必有序,但块与块之间必须“按块有序”,即第1快中的任一元素的关键字都必须小于第2块中任一元素的关键字;而第2块中任一元素又都小于第3块中的任一元素,……
查找分两部分:先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;然后在已确定的快中用顺序法进行查找。
@AllArgsConstructor
class IndexItem {public int index; //值比较的索引public int start; //开始位置public int length;//块元素长度(非空)
}public int indexSearch(int key){int[] mainList = new int[]{22, 12, 13, 8, 9, 20, 33, 42, 44, 38, 24, 48,60, 58, 74, 49, 86, 53}IndexItem[] indexItemList = new IndexItem[]{new IndexItem(22,1,6),new IndexItem(48,7,6),new IndexItem(86,13,6);}// 第一步,查找在哪一块int index = 0;for(;index < indexItemList.length; index++){if(indexItemList[index].index >= key ) break;} int num = 0;for(int i=0; i<index; i++){num += indexlist[i].length;}for(int i=num; i<num+indexItemList.length; i++){if(MainList[i] == key) return i;}return -1;
}
- 时间复杂度:O(log(m)+n/m),n个数据分成m块
- 平均查找长度:ASL=ASL折半查找+ASL顺序查找=log2log_2log2(m+1) +(n/m+1)/2
4. 二叉排序树BST
private static class BinaryTreeNode {int data;BinaryTree lchild;BinaryTree rchild;}public class BinarySearchTree {public static BinaryTreeNode serachBinaryTree(BinaryTreeNode btn, int key) {if (btn == null) { // 树节点不存在,返回return new BinaryTreeNode();} else if (key == btn.data) { // 查找成功return btn;} else if (key < btn.data) { // 关键字小于根节点查找左子树return serachBinaryTree(btn.lchild, key);} else { // 关键字大于根节点查找右子树return serachBinaryTree(btn.rchild, key);}}
}
- 时间复杂度:O(logn)
- 空间复杂度:O(1)
- 平均查找长度ASL:查找成功的平均查找长度、查找失败的平均查找长度
5. 哈希表查找
常用的哈希函数
- 直接地址法:H(key)=key或H(key)=a*key+b
- 除留余数法:H(key)= key mod p
- 数字分析法:可选取关键字的若干数位组成哈希地址,原则是使得到的哈希地址尽量避免冲突。
- 平方取中法:取关键字平方后的中间几位为哈希地址
常用的处理冲突方法- 开发地址法:有线性探查法和平方探查法
- 链式地址法:把所有的同义词用单链表链接起来的方法,种方哈希表中每个单元中存放的不再是记录本身,而是相应同义词单链表的头指针。
- 时间复杂度:O(1)
- 空间复杂度:O(n)
二、排序
注意:下标都是从1开始的
1. 不带哨兵的直接插入排序
public void InsertSort(int nums[]){int temp;for(int i=2; i<nums.length; i++){temp = nums[i];int j = i;while(nums[j]<nums[j-1] && j > 1){nums[j] = nums[j-1];}nums[j+1] = temp;}
}
- 时间复杂度:最差时间复杂度O(n2)、平均时间复杂度O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定
2. 带哨兵的直接插入排序
public void InsertSort(int nums[]){for(int i=2; i<nums.length; i++){nums[0] = nums[i];int j = i;while(nums[j]<nums[j-1]){nums[j] = nums[j-1];}nums[j+1] = nums[0];}
}
- 时间复杂度:最差时间复杂度O(n2)、平均时间复杂度O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定
3. 带哨兵、折半查找的直接插入排序
折半查找跟顺序查找的效率都是一样的,因为将元素向后退的次数是一样的。
public void InsertSort(int nums[]){int low,high,mid;for(int i=2;i<=n;i++){A[0]=A[i];low=1;high=i-1;while(low<=high){mid=(low+high)/2;if(A[mid]>A[0]) high=mid-1; //可用A[0],也可用A[i]else low=mid+1}for(int j=i-1;j>=high+1;--j) //注意这里只能用high,不能用low,midA[j+1]=A[j];A[high+1]=A[0];}
}
- 时间复杂度:最差时间复杂度O(n2)、平均时间复杂度O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定
4. 希尔排序
先追求表中元素的部分有序,再逐渐逼近全局有序。
public void ShellSort(int arr[], int gap){while(gap>=1){for(int i=0; i<gap; i++){for(int j=i+gapl j<arr.length; j+=gap){int temp = arr[i];for(int k = j-gap; k>=i&&arr[k]>temp; k-=gap){arr[k+gap] = arr[k];}arr[k+gap] = temp;}}}
}
- 时间复杂度:O(n1.3~2)
- 空间复杂度:O(1)
- 稳定性:不稳定
5. 冒泡排序
public static void BubbleSort(int nums[]){for(int i = 1; i< nums.length; i++){boolean flag = true;for(int j = 0; j<nums.length-i; j++){if(arr[j] > arr[j+1]){int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;flag = false;}}if(flag) break;}
}
- 时间复杂度:最坏时间复杂度O(n2)、平均时间复杂度O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定
6. 快速排序
public void quickSort(int[] nums, int left, int right){while(left >= right) return;int pivot = a[left];int i=left;int j=right;while(i < j){while(pivot <= a[j] && i<j) j--;while(pivot >= a[i] && i<j) i++;int temp = a[i];a[i] = a[j];a[j] = temp;}a[left] = a[i];a[i] = pivot;quickSort(a,left,i-1);//对左边的子数组进行快速排序quickSort(a,i+1,right);//对右边的子数组进行快速排序
}
- 时间复杂度:最差时间复杂度O(n2)、平均时间复杂度O(n2)
- 空间复杂度:O(log2n)~O(n)
- 稳定性:不稳定
7. 选择排序
public void SelectSort(int[] nums){for(int i=0; i<nums.length; i++){int temp = i;for(int j=i+1; j<nums.length; j++){if(nums[j] < nums[temp]) temp = j;}int swap = nums[i];nums[i] = nums[temp];nums[temp] = swap;}
}
- 时间复杂度:最差时间复杂度O(n2)、平均时间复杂度O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定
8. 堆排序
堆排序分为两个过程:输出堆顶、调整新堆
void HeadAdjust(int A[],int k,int len){ //调整指定根节点A[k]A[0]=A[k];for(int i=k*2;i<=len;i*=2){if(i<len&&A[i]<A[i+1]) i++; //不管要不要交换,先选出最大的子结点if(A[0]>=A[i]) break; //不用交换,而且后面是一定调整好的了else{A[k]=A[i]k=i; //这里与A[K]=A[0]相呼应,其实也可以选择A[i]=A[0],每次都交换}}A[k]=A[0];
}void BuildMaxHeap(int A[],int len){ //从最后一个子树根节点开始调整,调整全部根节点for(int i=len/2;i>0;--i) HeadAdjust(A,i,len);
}void HeapSort(int A[],int len){BuildMaxHeap(A,len); //堆初始化for(i=len;i>1;i--){ Swap(A[i],A[1]); //将最大值放在最后,然后重新在指定位置调整HeapAdjuest(A,1,i-1) //截断最后一位,并且重新从第一位调整}
}
- 时间复杂度:最差时间复杂度O(nlog2n)、平均时间复杂度O(nlog2n)
- 空间复杂度:O(1)
- 稳定性:不稳定
9. 归并排序
把两个或多个已经有序的序列合并成一个
public static int[] sort(int[] a,int low,int high){int mid = (low+high)/2;if(low<high){sort(a,low,mid);sort(a,mid+1,high);//左右归并merge(a,low,mid,high);}return a;}public static void merge(int[] a, int low, int mid, int high) {int[] temp = new int[high-low+1];int i= low;int j = mid+1;int k=0;// 把较小的数先移到新数组中while(i<=mid && j<=high){if(a[i]<a[j]){temp[k++] = a[i++];}else{temp[k++] = a[j++];}}// 把左边剩余的数移入数组 while(i<=mid){temp[k++] = a[i++];}// 把右边边剩余的数移入数组while(j<=high){temp[k++] = a[j++];}// 把新数组中的数覆盖nums数组for(int x=0;x<temp.length;x++){a[x+low] = temp[x];}}
- 时间复杂度:最差时间复杂度O(nlog2n)、平均时间复杂度O(nlog2n)
- 空间复杂度:O(n)
- 稳定性:稳定
二叉树
1. 递归先序遍历
public static void preOrder(TreeNode root){if(root == null) return;System.out.println(root.value);if(root.left != null) PreOrder(root.left);if(root.right != null) PreOrder(root.right);
}
2. 非递归先序遍历
public static void preOrder(TreeNode root){Stack<TreeNode> stack = new Stack<TreeNode>();while(root != null || !stack.isEmpty()){while(root!=null){ // 1. 下去的时候System.out.println(root.value); // 访问stack.push(root); // 入栈root = root.left // 左孩子}if(!stack.isEmpty()){ // 2. 回来的时候root = stack.pop(); // 出栈root = root.right; // 右孩子}}
}
3. 递归中序遍历
public static void midOrder(TreeNode root){if(root == null) return;if(root.left != null) PreOrder(root.left);System.out.println(root.value);if(root.right != null) PreOrder(root.right);
}
4. 非递归中序遍历
public static void minOrder(TreeNode root){Stack<TreeNode> stack = new Stack<TreeNode>();while(root != null || !stack.isEmpty()){while(root!=null){ // 1. 下去的时候stack.push(root); // 入栈root = root.left // 左孩子}if(!stack.isEmpty()){ // 2. 回来的时候root = stack.pop(); // 出栈System.out.println(root.value); // 访问root = root.right; // 右孩子}}
}
5. 递归后序遍历
public static void postOrder(TreeNode root){if(root == null) return;if(root.left != null) PreOrder(root.left);if(root.right != null) PreOrder(root.right);System.out.println(root.value);
}
6. 非递归后序遍历
public void postorderTraversal(TreeNode root) {Deque<TreeNode> stack = new LinkedList<TreeNode>();TreeNode prev = null; // prev是指上一个遍历到的结点if (root == null) return res;while (root != null || !stack.isEmpty()) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();// 要是没有右孩子,或者右孩子已经看过了,就打印根结点if (root.right == null || root.right == prev) {System.out.println(root.value);prev = root; // 保留最近遍历过的一次结点root = null; //这里设为null,就是好好的把结点输出} // 右孩子不是空的,并且上次prev没有走过的,就push进栈。else{ stack.push(root);root = root.right;}}
}
7. 广度遍历二叉树
public static void bfs(TreeNode root){Queue<TreeNode> queue = new LinkedList<TreeNode>();if(root == null) return;queue.add(root);while(!queue.isEmpty()){TreeNode t = queue.remove();System.out.println(root.value); if(t.left != null) queue.add(t.left);if(t.right != null) queue.add(t.right);}
}
8. 深度遍历
public void dfs(TreeNode root){Stack<TreeNode> stack=new Stack<TreeNode>();if(root==null)return list;//压入根节点stack.push(root);//然后就循环取出和压入节点,直到栈为空,结束循环while (!stack.isEmpty()){TreeNode t=stack.pop();if(t.right!=null)stack.push(t.right);if(t.left!=null)stack.push(t.left);System.out.println(t.value);}
}
相关文章:

查找、排序、二叉树的算法,统统记录于此。
文章目录一、查找1. 无序表的顺序查找2. 折半查找3. 分块查找4. 二叉排序树BST5. 哈希表查找二、排序1. 不带哨兵的直接插入排序2. 带哨兵的直接插入排序3. 带哨兵、折半查找的直接插入排序4. 希尔排序5. 冒泡排序6. 快速排序7. 选择排序8. 堆排序9. 归并排序二叉树1. 递归先序…...

如何用Python实现在网页中嵌入YouTube的视频?
要在网页中嵌入YouTube视频,可以使用HTML代码,在Python中使用字符串拼接的方式生成HTML代码。下面是一个示例代码,可以生成嵌入YouTube视频的HTML代码: def embed_youtube_video(video_id, width560, height315): """ 生成嵌…...
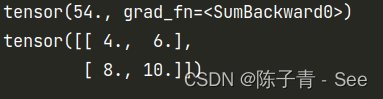
Easy Deep Learning——PyTorch中的自动微分
目录 什么是深度学习?它的实现原理是怎么样的呢? 什么是梯度下降?梯度下降是怎么计算出最优解的? 什么是导数?求导对于深度学习来说有何意义? PyTorch 自动微分(自动求导) 为什么…...

【生物信息】利用ChatGPT解释GO分析中的关于Biological Processes的问题
利用ChatGPT解释GO分析中的一些问题 如何理解GO中的evidence:ISS,这是什么?qualifier:involved_in是什么意思?evidence:TAS是什么?evidence: IBA是什么?evidence: IMP是什么?evidence:IDA是什么?evidence: IEA是什么?GO分析中,evidence: NAS是什么意思?GO分析中…...

2018年MathorCup数学建模C题陆基导弹打击航母的数学建模与算法设计解题全过程文档及程序
2018年第八届MathorCup高校数学建模挑战赛 C题 陆基导弹打击航母的数学建模与算法设计 原题再现: 火箭军是保卫海疆主权的战略力量,导弹是国之利器。保家卫国,匹夫有责。为此,请参赛者认真阅读"陆基反舰导弹打击航母的建模示意图"。(附图 1 )参考图中的…...
打怪升级之CFile类
CFile类 信息源自官方文档:https://learn.microsoft.com/zh-cn/cpp/mfc/reference/cfile-class?viewmsvc-170。 CFile是Microsoft 基础类文件类的基类。它直接提供非缓冲的二进制磁盘输入/输出设备,并直接地通过派生类支持文本文件和内存文件。CFile与…...

[css]通过网站实例学习以最简单的方式构造三元素布局
文章目录二元素布局纵向布局横向布局三元素布局b站直播布局实例左右-下 布局左-上下 布局上下-右 布局方案一方案二后言二元素布局 在学习三元素布局之前,让我们先简单了解一下只有两个元素的布局吧 两个元素的相对关系非常简单,不是上下就是左右 纵向布…...
【冲刺蓝桥杯的最后30天】day6
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始更新备战蓝桥30天系列,一共30天,如果对你有帮助或者正在备…...
ssm框架之spring:浅聊IOC
IOC 前面体验了spring,不过其运用了IOC,至于IOC( Inverse Of Controll—控制反转 ) 看一下百度百科解释: 控制反转(Inversion of Control,缩写为IoC),是面向对象编程中的一种设计原则&#x…...
pytest初识
一、单元测试框架 (1)什么是单元测试框架? 单元测试是指在软件开发中,针对软件的最小单元(函数、方法)进行正确性的检查测试 (2)单元测试框架 java:junit和testng pytho…...
-12)
设计模式~责任链模式(Chain of Responsibility)-12
目录 (1)优点 (2)缺点 (3)使用场景 (4)注意事项: (5)应用实例: (6)经典案例 代码 责任链, …...

【ElasticSearch】(一)—— 初识ES
文章目录1. 了解ES1.1 elasticsearch的作用1.2 ELK技术栈1.3 elasticsearch和lucene1.4 为什么不是其他搜索技术?1.5 总结2. 倒排索引2.1 正向索引2.2 倒排索引2.3 正向和倒排3. ES的一些概念3.1 文档和字段3.2 索引和映射3.3 mysql与elasticsearch1. 了解ES Elasti…...
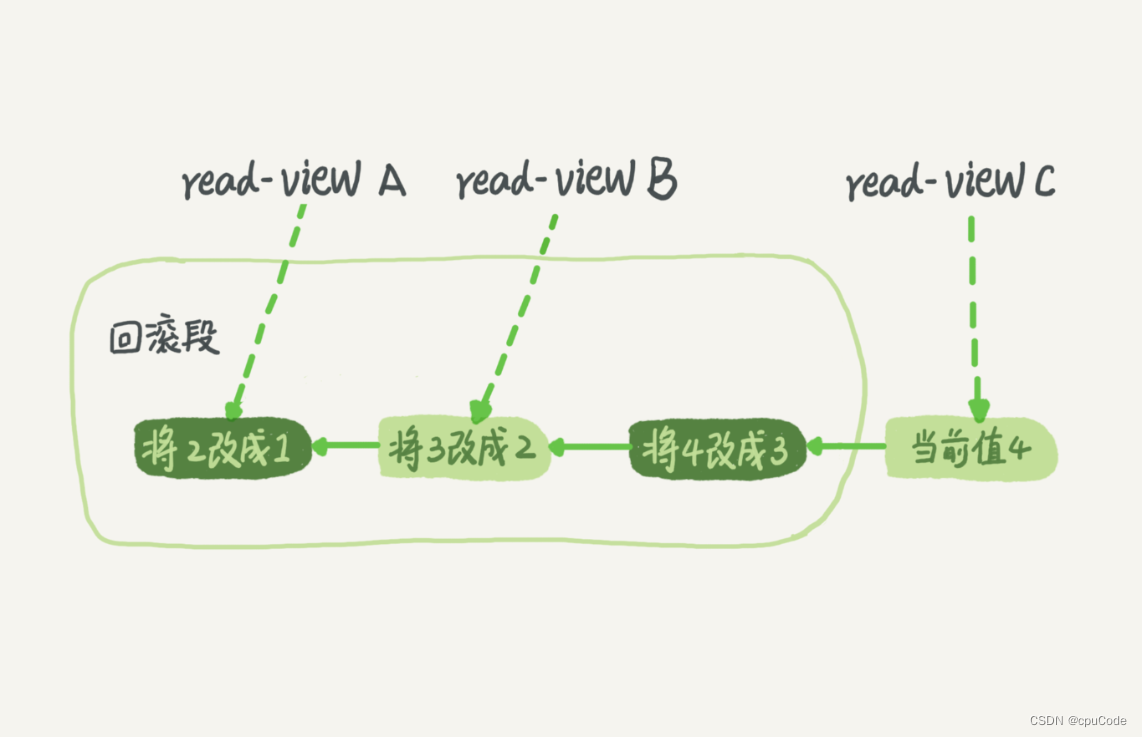
MySQL 事务隔离
MySQL 事务隔离事务隔离实现事务的启动ACID : 原子(Atomicity)、一致(Consistency)、隔离(Isolation)、永久(Durability) 多个事务可能出现问题 : 脏读 (dirty read) , 不可重复读 (non-repeatable read) , 幻读 (phantom read) 事务隔离级别 : 读未提交 (read uncommitted)…...

基础06-JS中for-in和for-of有什么区别
for…in 和 for…of 的区别 题目 for…in 和 for…of 的区别 key 和 value for…in 遍历 key , for…of 遍历 value const arr [10, 20, 30] for (let n of arr) {console.log(n) }const str abc for (let s of str) {console.log(s) }function fn() {for (let argument…...

AI视频智能分析EasyCVR视频融合平台录像计划模块搜索框细节优化
EasyCVR支持海量视频汇聚管理,可提供视频监控直播、云端录像、云存储、录像检索与回看、智能告警、平台级联、智能分析等视频服务。在录像功能上,平台可支持: 根据业务场景自定义录像计划,可支持7*24H不间断录像,支持…...
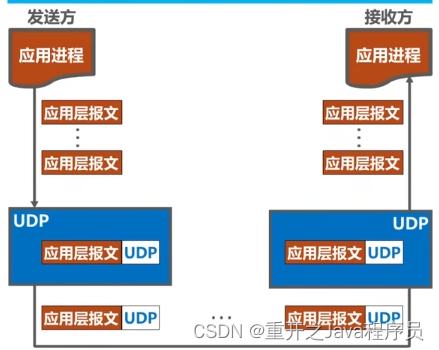
TCP和UDP对比
TCP和UDP对比 UDP(用户数据报协议) 无连接(指的是逻辑连接关系,不是物理上的连接) 支持单播、多播以及广播,也就是UDP支持一对一、一对多、一对全 面向应用报文的,对应用层交付的报文直接打包 无连接不可靠的传输服务(适用于IP电话、视频会议等实时应用),不使用流量控制和…...

CVS Health 西维斯健康EDI需求
CVS Health西维斯健康在特拉华州成立,通过旗下的 CVS Pharmacy 和 Longs Drugs 零售店以及 CVS.com 电商提供处方药、美容产品、化妆品、电影和照片加工服务、季节性商品、贺卡和方便食品。CVS Health通过使高质量的护理变得更经济、更易获得、更简单、更无缝&#…...
Anaconda配置Python科学计算库SciPy的方法
本文介绍在Anaconda环境中,安装Python语言SciPy模块的方法。 SciPy是基于Python的科学计算库,用于解决科学、工程和技术计算中的各种问题。它建立在NumPy库的基础之上,提供了大量高效、易于使用的功能,包括统计分析、信号处理、优…...
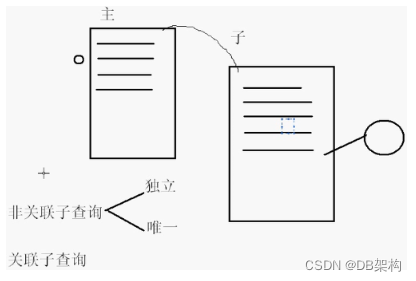
数据库基本功之复杂查询的子查询
子查询返回的值可以被外部查询使用,这样的复合查询等效与执行两个连续的查询. 1. 单行单列子查询 (>,<,,<>,>,<)内部SELECT子句只返回一行结果 2.多行单列子查询 (all, any, in,not in) all (>大于最大的,<小于最小的) SQL> select ename, sal from…...

脑机接口科普0019——大脑的分区及功能
本文禁止转载!!!! 在前文脑机接口科普0018——前额叶切除手术_sgmcy的博客-CSDN博客科普中,有个这样的一张图: 这个图呢,把大脑划分为不同的区域,然后不同的区域代表不同的功能。 …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...