现代信号处理11_Spectral Analysis谱分析(CSDN_20240526)
谱分析与傅里叶变换
对于一个信号,一方面可以从时域上对其进行分析,另一方面也可以从频域上对其进行认识,对信号进行频谱分析能够帮助我们了解能量在频域上的分布。




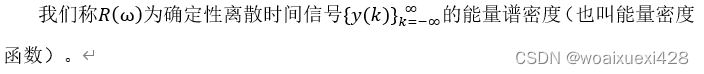


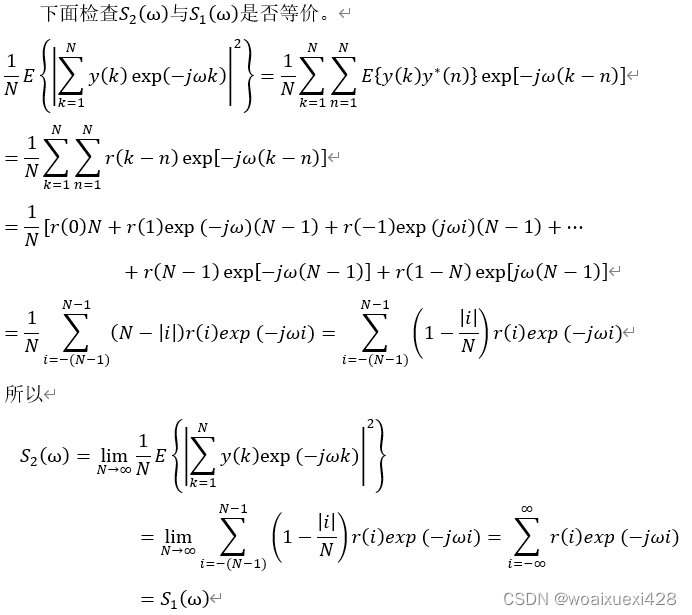
确定性信号的能量通常是有限的,而平稳随机信号的能量通常是无限的,因此对于随机信号而言,我们通常不研究它的能量,而是研究它的功率,只要功率有限,就可以定义功率谱,功率谱的含义是将功率散布在不同的频率上。
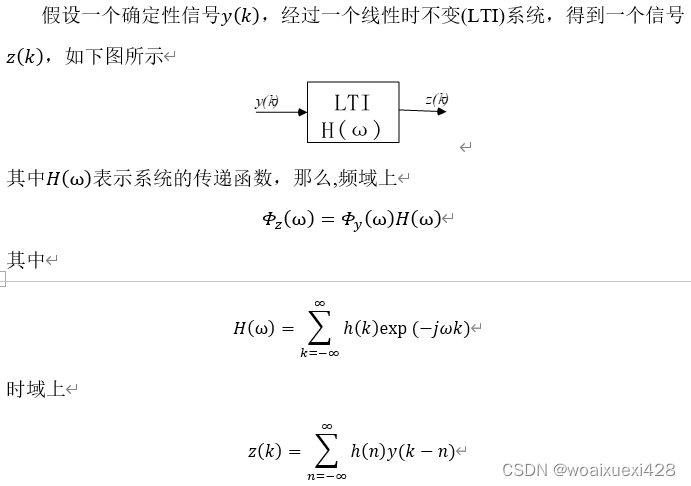

周期图谱估计

- 定义要求使用无限长度的数据得到相关值,然后再求功率谱,然而无限长度的数据是无法获取的。
- 根据定义,相关是在固定时间上做统计平均,然而在现实中不能固定时间。解决这个问题的方法是用时间平均近似统计平均,这种近似的前提是yn 满足各态历经性。另外即使yn
 满足各态历经性,估计精度也受到数据长度有限的约束。
满足各态历经性,估计精度也受到数据长度有限的约束。

周期图估计存在的问题
均值


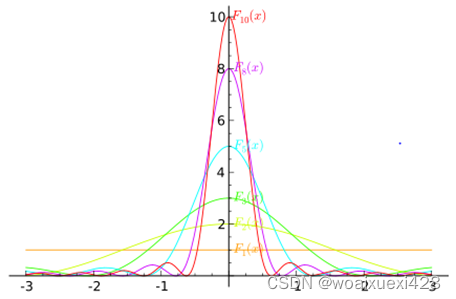
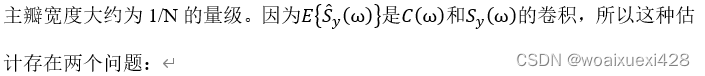
- 分辨率(Resolution)下降
- 频谱泄露(Leakage)
增加数据长度N,上面的两个问题会有所改善。
方差


至此,可以看出,周期图谱法的主要问题存在于方差之上。因为谱估计的均值存在的问题是分辨率降低和频谱泄露,但这两者可以通过增加采样数据可以有效改善。然而估计的方差与采样数据的长度无关,而且我们已经知道问题出现的原因是周期图谱估计中直接放弃了期望,所以为了改善方差,就必须想办法,将求期望再放回估计中。对于有限个数据N,为了模拟没忽略的求期望过程,可以将数据分成若干组,分别对每组数据进行估计,然后再求均值,这样可以明显改善估计的方差,但是由于数据段变短,对加剧估计均值中的分辨率问题和泄露问题,因此这里要根据实际需求,在均值和方差之间做一个合理的tradeoff。
小结
谱分析在信号处理中占有重要地位。对于确定性信号,以傅里叶分析为基础,用傅里叶积分或傅里叶级数表达信号的谱特征。对于随机信号,由于收敛性问题而无法直接对信号作傅里叶积分或傅里叶级数,通常,傅里叶积分或傅里叶级数作用在随机信号的相关函数上。相对于信号本身而言,信号的相关函数不是那么直接,但通过Wienner-Khinchine关系,就可以像处理确定性信号一样处理随机信号。但是对随信号作傅里叶积分或傅里叶级数后,得到的是一个随机变量,这就意味着每次试验的结果都是不一样的,存在较大的起伏和不确定性。那么这个随机变量能够多大程度地近似实际的谱特征呢?实际上,这个近似无论从均值上还是从方差上都存在问题。首先,对于均值,由于数据是有限的,谱估计会存在分辨率下降和频谱泄露的问题,幸运的是,这个问题可以通过增加数据长度得到有效改善。其次,对于方差,增加数据长度并不会减小方差,为了减小方差,我们只能把得到的有限的数据分成若干组进行处理,然后去平均。分的组越多,方差改善越明显,但是分的组越多,每段数据的长度就越短,分辨率和频谱泄露就会被恶化,因此这里我们要根据实际需要,做均值和方差之间的tradeoff。
------------------------------------------------------------------------------------------------
因为文档中公式较多,不方便编辑,所以本文使用截图的方式展现。如需电子版文档,可以通过下面的链接进行下载。
链接![]() http://generatelink.xam.ink/change/makeurl/changeurl/11779
http://generatelink.xam.ink/change/makeurl/changeurl/11779
相关文章:
现代信号处理11_Spectral Analysis谱分析(CSDN_20240526)
谱分析与傅里叶变换 对于一个信号,一方面可以从时域上对其进行分析,另一方面也可以从频域上对其进行认识,对信号进行频谱分析能够帮助我们了解能量在频域上的分布。 确定性信号的能量通常是有限的,而平稳随机信号的能量通常是无限…...
C#开发上位机应用:基础与实践
C#是一种流行的面向对象编程语言,常用于Windows应用程序的开发。上位机应用是一种用于监控和控制设备或系统的应用程序,通常与下位机(如传感器、执行器等)进行通信。在本文中,我们将介绍C#开发上位机应用的基础知识和实…...
话术巧妙分隔沟通效果更佳看看这个小技巧
客服回复客户咨询,如果遇到比较复杂的问题,经常会有大段的文字回复,用聊天宝的分段符功能,在需要分段的地方点击右上角的“插入分隔符”,就可以在指定位置分段,实现多段发送的目的。 前言 客服回复客户咨询…...
)
【Spring】设计模式(GOF)
Spring Framework在其架构和实现中广泛使用了多种GOF(Gang of Four)设计模式。这些设计模式帮助Spring解决了许多常见的软件开发问题,提高了代码的可重用性、可维护性和可扩展性。 1、工厂模式(Factory Pattern) 1.1简…...

php抖音详情和关键词搜索api
抖音详情和关键词搜索的 API 可以通过抖音提供的开放平台来获取。以下是使用 PHP 实现的示例代码: 获取抖音视频详情 API: 获取Key和secret请移步 <?php$accessToken YOUR_ACCESS_TOKEN; // 替换为自己的 access_token $itemId YOUR_ITEM_ID; /…...

SOCKS 代理 和 HTTP 代理
SOCKS 代理 和 HTTP 代理 的区别 SOCKS 代理 和 HTTP 代理 都是代理服务器,它们充当客户端和目标服务器之间的中介,但它们的工作方式和应用场景有所不同。 1. SOCKS 代理: 工作原理: SOCKS 代理是一种更底层的代理,…...
【Linux】自己实现一个bash进程
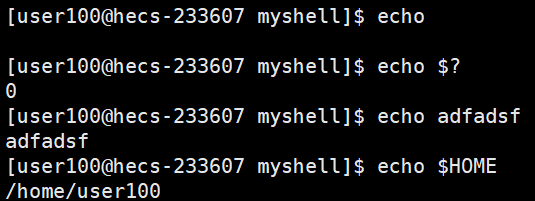
bash就是命令行解释器,就是Linux操作系统让我们看到的,与用户进行交互的一种外壳(shell),当然了bash也是一个进程,它有时候就是通过创建子进程来执行我们输入的命令的。这无疑就离不开我们上篇博客所说的进…...
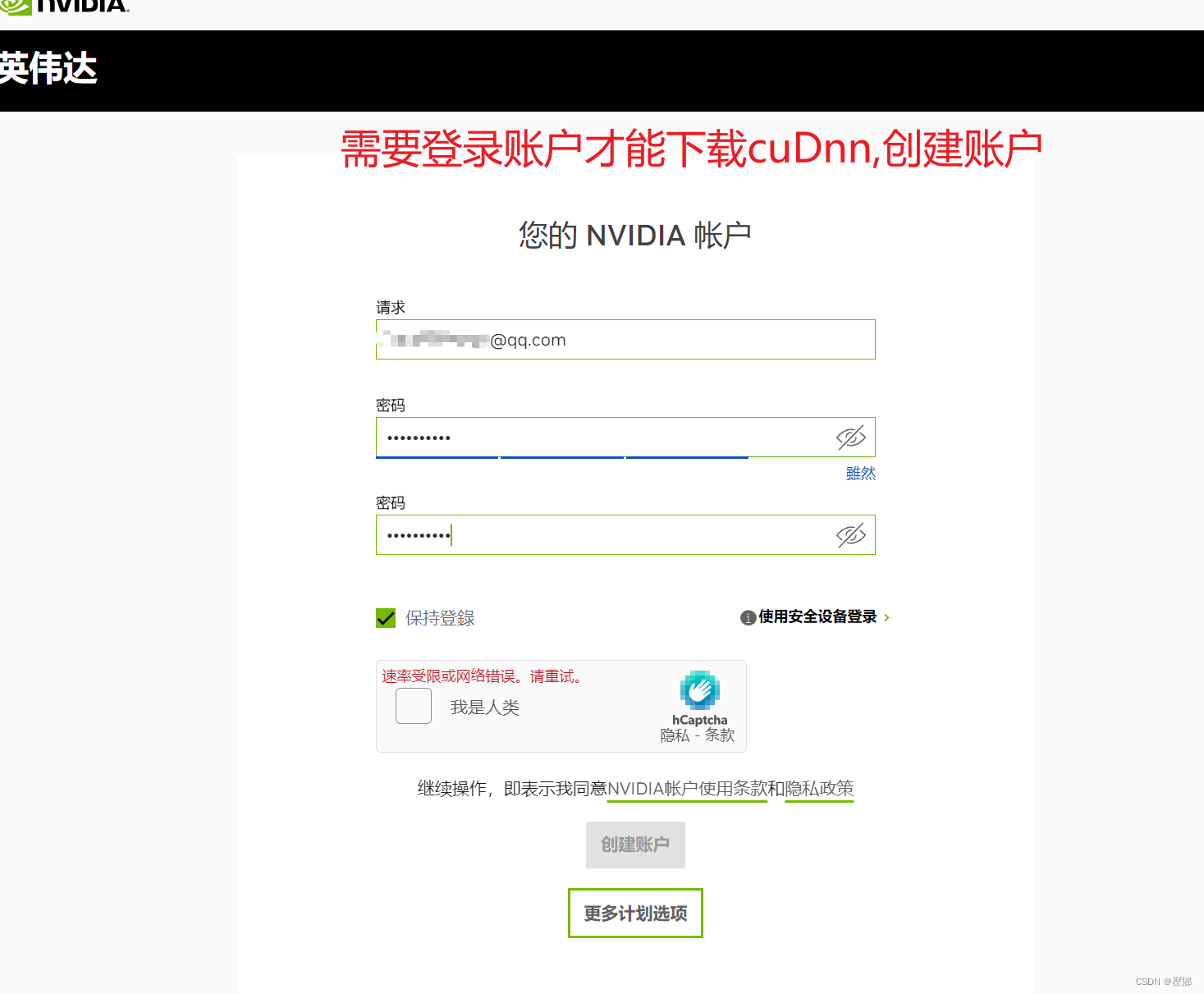
记录深度学习GPU配置,下载CUDA与cuDnn
目标下载: cuda 11.0.1_451.22 win10.exe cudnn-11.0-windows-x64-v8.0.2.39.zip cuda历史版本网址 CUDA Toolkit Archive | NVIDIA Developer 自己下载过11.0.1版本 点击下载local版本,本地安装,有2个多GB,很大,我不喜欢network版本,容易掉线 cuDnn https://developer.nvi…...
Word将表格调成合适的大小
请等待内容完善...

2024HBCPC:C Goose Goose Duck
题目描述 Iris 有 n n n 个喜欢玩鹅鸭杀的朋友,编号为 1 ∼ n 1∼n 1∼n。 假期的时候,大家经常会在群里问有没有人玩鹅鸭杀,并且报出现在已经参与的人数。 但是每个人对于当前是否加入游戏都有自己的想法。 具体的来说,对于第…...

Llama 3 模型家族构建安全可信赖企业级AI应用之使用 Llama Guard 保护大模型对话 (八)
LlaMA 3 系列博客 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (一) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (二) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (三) 基于 LlaMA…...

《一地霜白》读书笔记
1.3.6 街灯明灭,勾缀成行,为了生者与死者 “很多年过去了。回头看,沿着一排暗中的街灯,两三盏灭了,郁闷中有意外的欣喜:街灯明灭,勾缀成行,为了生者与死者。” 童年、青少年在人的…...

在Java中实现多线程之间的通信
一、技术难点 在Java中实现多线程之间的通信是一个复杂但重要的任务,它涉及到线程同步、数据共享和线程间协作等多个方面。以下是实现多线程通信时可能遇到的一些技术难点: 线程同步:多线程环境下,多个线程可能同时访问和修改共享…...

Python中的json.dump与json.dumps对比
Python中的json.dump与json.dumps对比 json.dumps()json.dump() json.dumps() dumps 是 “dump string” 的缩写。它将Python对象转换(序列化)为JSON格式的字符串。数据被转换为一个字符串,并且这个字符串可以直接被写入文件、发送到网络&am…...

【从零开始学习RabbitMQ | 第二篇】如何确保MQ的可靠性和消费者可靠性
目录 前言: MQ可靠性: 数据持久化: Lazy Queue: 消费者可靠性: 消费者确认机制: 消费失败处理: MQ保证幂等性: 方法一: 总结: 前言: …...
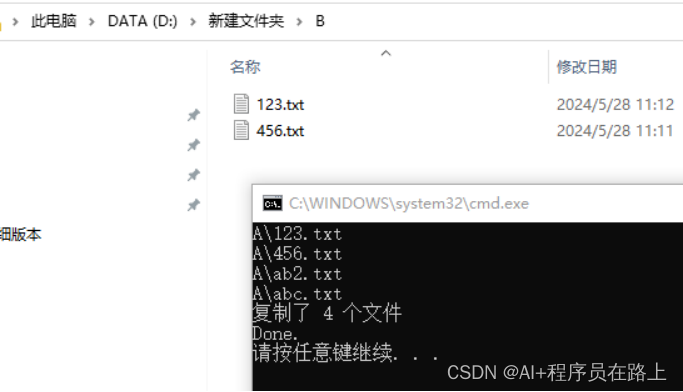
常用批处理命令及批处理文件编写技巧
一常用批处理命令 1.查看命令用法:命令 /? //如:cd /? 2.切换盘符目录:cd /d D:\test 或直接输入 d: //进入上次d盘所在的目录 3.切换目录:cd test 4.清屏:cls 5.“arp -a” //它会列出当前设备缓存中的所有…...

android NetworkMonitor记录
是否能上网的状态 上网url地址的设置: NetworkMonitor.java makeCaptivePortalHttpsUrls config_captive_portal_https_urls DEFAULT_CAPTIVE_PORTAL_HTTPS_URLS http准备监测 isCaptivePortal sendHttpAndHttpsParallelWithFallbackProbes httpsProbe.start();…...

OSPF优化——OSPF减少LSA更新量2
二、特殊区域——优化非骨干区域的LSA数量 不是骨干区域、不能存在虚链路 1、不能存在 ASBR 1)末梢区域 该区域将拒绝 4、5LSA的进人,同时由该区域连接骨干0区域的ABR 向该区域,发布一条3类的缺省路由; 该区域内每台路由器均需配置…...

【AMS】Android 8.0+ 绕开启动后台Service限制
一、背景 应客户要求,需要在开机时,拉起应用A。但因为开机时,同时被拉起的应用过多,导致Launcher在开机那一刻较为卡顿。为解决这一问题,采取了延迟拉起的做法。在开机后,延迟一定时间,由系统服务,拉起应用A。 于是乎,就出现这么个报错: Not allowed to start ser…...
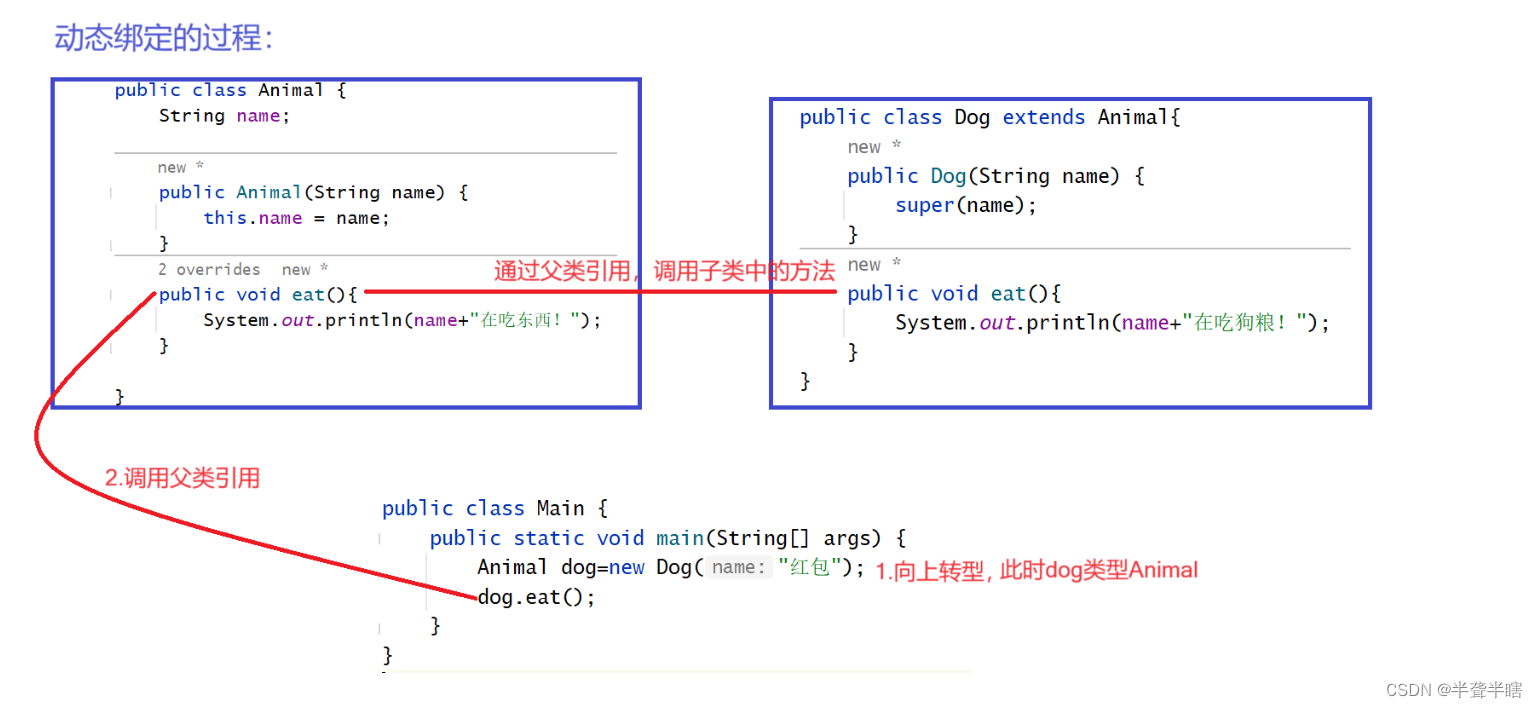
【多态】(超级详细!)
【多态】(超级详细!) 前言一、 多态的概念二、重写1. 方法重写的规则2. 重写和重载的区别 三、多态实现的条件四、 向上转型五、动态绑定 前言 面向对象的三大特征:封装性、继承性、多态性。 extends继承或者implements实现&…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
