浅说线性DP(上)
前言
在说线性dp之前,我们先来聊一聊动态规划是啥?
动态规划到底是啥?
动态规划是普及组内容中最难的一个部分,也是每年几乎必考的内容。它对思维的要求极高,它和图论、数据结构不同的地方在于它没有一个标准的数学表达式和明确清晰的解题方法。
动态规划是对求解最优解的一种途径,而不是一种特殊的算法。由于各种问题的性质不同,确定最优解的条件也互不相同,因而动态规划的设计方法对不同的问题,有各具特色的阶梯方法,而不存在一种万能的动态规划算法。为了方便学习,我们把若干具有代表性的动态规划问题归纳总结成不同的几类,并建立对应的数学模型。
动态规划一般用来求解多阶段决策问题的最优解,可以将过程分成若干个互相联系的阶段,在它的每一阶段都需要做决策,从而使整个过程达到最好的活动效果。各个阶段决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展,当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线。
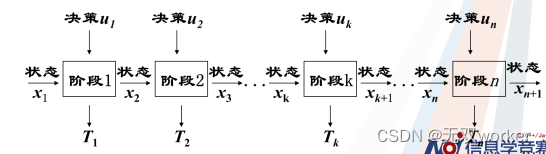
对于动态规划问题,最重要的是分析出:
一、决策对象:我们需要对题目中的哪个变量进行决策。
二、阶段:需要将问题的全过程恰当的分成若干个相互联系的阶段,以便按一定的次序去求解。阶段的划分一般是根据时间(先后顺序) 和 空间(大小关系) 的自然特征来划分。
三、状态:某一阶段的出发位置称为状态,一个阶段可能包含多个状态,状态大多都是用 数组 来表示,即表示我们需要的答案。
四、决策:分析完问题后我们应该怎么解决问题。
五、状态转移方程:描述前一阶段到后一阶段的状态演变规律。
线性动态规划
线性动态规划是动态规划中比较简单的一类问题,他的状态转移是线性的,即状态的转移是固定的,常见的如从前到后,或者从后到前。线性动态规划和递推比较类似,在很多情况下,这两种做法大致是相同的。一般的,递推是当前要求解的答案和前面某个固定答案有关,而线性动态规划是当前答案和前面的某个答案存在关系,这个位置在不同的情况下是不相同的。
最长上升子序列
言归正传,我们继续聊线性dp。
子集和子序列和子串的区别
以 a b f s g e g s a s abfsgegsas abfsgegsas为例, f a g g a s faggas faggas是它的子集,因为子集是不计顺序的, a b g g s s abggss abggss 则是他的子序列,因为子序列是要求有顺序的,而 a b f abf abf则是他的字串
内容分析
决策对象
每个位置上的数。
阶段
共有 n n n 个数,因此有 n n n 个阶段。
状态
因为每个数都有可能是子序列的结尾,所以使用 dp[i] 表示以第 i i i 个数作为结尾的最长上升子序列的长度。
决策
如果以第 i i i 个数作为结尾,那么在这个序列中,上一个数一定要小于 a [ i ] a[i] a[i]。因此,我们需要在前面的数中找到比 a [ i ] a[i] a[i] 小的数,而且我们应该选择以这个数结尾的最长上升子序列中最长的那个,这样接在这个数后面得到的序列也是最长的。
状态转移方程
如果 h [ k ] < h [ i ] h[k]<h[i] h[k]<h[i],则 d p [ i ] = m a x ( d p [ i ] , d p [ k ] + 1 ) dp[i]=max(dp[i],dp[k]+1) dp[i]=max(dp[i],dp[k]+1),其中 k ∈ [ 1 , i − 1 ] k\in[1,i-1] k∈[1,i−1]。
最后,我们找到最大的 d p [ i ] dp[i] dp[i] 就是答案。
#include<bits/stdc++.h>
using namespace std;int a[10010],dp[10010],ans=INT_MIN;
int main(){int n;cin>>n;for (int i=1;i<=n;i++){cin>>a[i];dp[i]=1;} for (int i=1;i<=n;i++){for (int j=1;j<i;j++){if (a[j]<a[i]){dp[i]=max(dp[i],dp[j]+1);}}ans=max(ans,dp[i]);}cout<<ans;return 0;
}
相关文章:

浅说线性DP(上)
前言 在说线性dp之前,我们先来聊一聊动态规划是啥? 动态规划到底是啥? 动态规划是普及组内容中最难的一个部分,也是每年几乎必考的内容。它对思维的要求极高,它和图论、数据结构不同的地方在于它没有一个标准的数学…...

leetcode题目18
四数之和 中等 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复)…...

后端企业级开发之yaml数据序列化格式文件详解2024
yaml格式 数据格式 yaml 是一种数据序列化的格式 容易阅读 容易与脚本语言交互 以数据为核心 重数据轻格式 我们要知道他怎么书写 大小写敏感 属性层级关系使用多行描述 每行结尾使用冒号结束 使用缩进表示层级关系 同层级左侧对其 只运行使用空格 属性前面添加空格 #表…...

智能界面设计:数字孪生与大数据结合的美学典范
智能界面设计:数字孪生与大数据结合的美学典范 引言 在数字化浪潮的推动下,智能界面设计成为了连接用户与技术的重要桥梁。数字孪生技术与大数据的结合,不仅为UI设计带来了前所未有的创新机遇,更成为了美学与功能性融合的典范。…...

听说部门来了个00后测试开发,一顿操作给我整麻了
公司新来了个同事,听说大学是学的广告专业,因为喜欢IT行业就找了个培训班,后来在一家小公司实习半年,现在跳槽来我们公司。来了之后把现有项目的性能优化了一遍,服务器缩减一半,性能反而提升4倍!…...

Linux shell命令
cat 文件名 查看文件内容, tac文件名 倒着显示。 more 文件名 显示内容 less文件名 和more的功能一样,按上下左右键,按Q键结束。 head文件名,只显示前10行内容。 ln是一个默认创建硬链接的命令 ln 文件名 ls -i文件名…...

【Linux】Linux基本指令1
1.软件,OS,驱动 我们看看计算机的结构层次 1.1.操作系统 操作系统是一款做 软硬件管理 的软件 操作系统(计算机管理控制程序)_百度百科 (baidu.com) 操作系统(英语:Operating System,缩写&a…...
重学java 49 增强for
知之俞明,则行之越笃;行之愈笃,则知之愈益; —— 24.5.28 一、基本使用 1.作用: 遍历集合或者数组 2.格式: for(元素类型 变量名:要遍历的集合名或者数组名) 变量名就是代表的每一个元素 3.快捷键: 集合名或者数组名.for package …...

BUUCTF靶场[Web] [极客大挑战 2019]Havefun1、[HCTF 2018]WarmUp1、[ACTF2020 新生赛]Include
[web][极客大挑战 2019]Havefun1 考点:前端、GET传参 点开网址,发现是这个界面 点击界面没有回显,老规矩查看源代码,看到以下代码 代码主要意思为: 用get传参,将所传的参数给cat,如果catdog…...
现代信号处理11_Spectral Analysis谱分析(CSDN_20240526)
谱分析与傅里叶变换 对于一个信号,一方面可以从时域上对其进行分析,另一方面也可以从频域上对其进行认识,对信号进行频谱分析能够帮助我们了解能量在频域上的分布。 确定性信号的能量通常是有限的,而平稳随机信号的能量通常是无限…...
C#开发上位机应用:基础与实践
C#是一种流行的面向对象编程语言,常用于Windows应用程序的开发。上位机应用是一种用于监控和控制设备或系统的应用程序,通常与下位机(如传感器、执行器等)进行通信。在本文中,我们将介绍C#开发上位机应用的基础知识和实…...
话术巧妙分隔沟通效果更佳看看这个小技巧
客服回复客户咨询,如果遇到比较复杂的问题,经常会有大段的文字回复,用聊天宝的分段符功能,在需要分段的地方点击右上角的“插入分隔符”,就可以在指定位置分段,实现多段发送的目的。 前言 客服回复客户咨询…...
)
【Spring】设计模式(GOF)
Spring Framework在其架构和实现中广泛使用了多种GOF(Gang of Four)设计模式。这些设计模式帮助Spring解决了许多常见的软件开发问题,提高了代码的可重用性、可维护性和可扩展性。 1、工厂模式(Factory Pattern) 1.1简…...

php抖音详情和关键词搜索api
抖音详情和关键词搜索的 API 可以通过抖音提供的开放平台来获取。以下是使用 PHP 实现的示例代码: 获取抖音视频详情 API: 获取Key和secret请移步 <?php$accessToken YOUR_ACCESS_TOKEN; // 替换为自己的 access_token $itemId YOUR_ITEM_ID; /…...

SOCKS 代理 和 HTTP 代理
SOCKS 代理 和 HTTP 代理 的区别 SOCKS 代理 和 HTTP 代理 都是代理服务器,它们充当客户端和目标服务器之间的中介,但它们的工作方式和应用场景有所不同。 1. SOCKS 代理: 工作原理: SOCKS 代理是一种更底层的代理,…...
【Linux】自己实现一个bash进程
bash就是命令行解释器,就是Linux操作系统让我们看到的,与用户进行交互的一种外壳(shell),当然了bash也是一个进程,它有时候就是通过创建子进程来执行我们输入的命令的。这无疑就离不开我们上篇博客所说的进…...
记录深度学习GPU配置,下载CUDA与cuDnn
目标下载: cuda 11.0.1_451.22 win10.exe cudnn-11.0-windows-x64-v8.0.2.39.zip cuda历史版本网址 CUDA Toolkit Archive | NVIDIA Developer 自己下载过11.0.1版本 点击下载local版本,本地安装,有2个多GB,很大,我不喜欢network版本,容易掉线 cuDnn https://developer.nvi…...
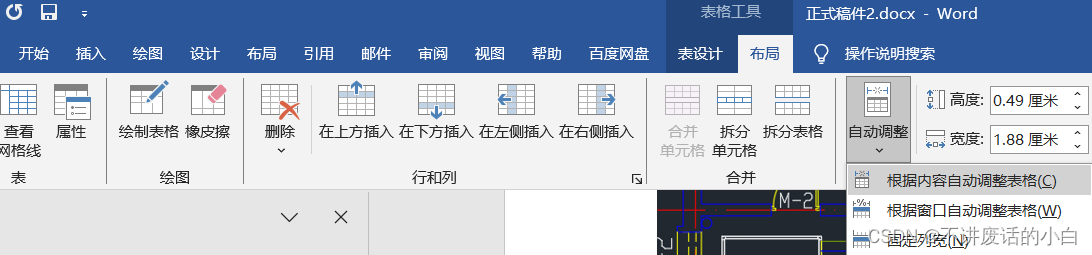
Word将表格调成合适的大小
请等待内容完善...

2024HBCPC:C Goose Goose Duck
题目描述 Iris 有 n n n 个喜欢玩鹅鸭杀的朋友,编号为 1 ∼ n 1∼n 1∼n。 假期的时候,大家经常会在群里问有没有人玩鹅鸭杀,并且报出现在已经参与的人数。 但是每个人对于当前是否加入游戏都有自己的想法。 具体的来说,对于第…...

Llama 3 模型家族构建安全可信赖企业级AI应用之使用 Llama Guard 保护大模型对话 (八)
LlaMA 3 系列博客 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (一) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (二) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (三) 基于 LlaMA…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
