代码随想录算法训练营第二十一天| 530. 二叉搜索树的最小绝对差、501. 二叉搜索树中的众数、236. 二叉树的最近公共祖先
[LeetCode] 530. 二叉搜索树的最小绝对差
[LeetCode] 530. 二叉搜索树的最小绝对差 文章解释
[LeetCode] 530. 二叉搜索树的最小绝对差 视频解释
题目:
给你一个二叉搜索树的根节点
root,返回 树中任意两不同节点值之间的最小差值 。差值是一个正数,其数值等于两值之差的绝对值。
示例 1:
输入:root = [4,2,6,1,3] 输出:1示例 2:
输入:root = [1,0,48,null,null,12,49] 输出:1提示:
- 树中节点的数目范围是
[2, 104]0 <= Node.val <= 10^5
[LeetCode] 530. 二叉搜索树的最小绝对差
自己看到题目的第一想法
先看了一眼文章解释, 被一句话点醒了~
看完代码随想录之后的想法
看到的第一句话就是: 二叉搜索树右子树节点的值都是大于等于左子树节点以及跟节点的值的. 这样的话就会立刻想起来, 一棵二叉搜索树的中序遍历序列是一个非递减的有序序列. 这样只需要在遍历的过程中,记录当前节点和前一个节点的差, 记录下最小的值即可.
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
// 递归法:
// 核心思想: 对于一个二叉搜索树, 中序遍历后, 遍历的序列是递增的.
class Solution {private TreeNode preNode;private int minmumDifference = -1;public int getMinimumDifference(TreeNode root) {if (root == null) {return -1;}int leftTreeMinimumDifference = getMinimumDifference(root.left);if (preNode != null && (minmumDifference == -1 || root.val - preNode.val < minmumDifference)) {minmumDifference = root.val - preNode.val;}preNode = root;int rightTreeMinimumDifference = getMinimumDifference(root.right);if (leftTreeMinimumDifference >= 0) {minmumDifference = Math.min(leftTreeMinimumDifference, minmumDifference);}if (rightTreeMinimumDifference >= 0) {minmumDifference = Math.min(rightTreeMinimumDifference, minmumDifference);}return minmumDifference;}
}/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
// 迭代法: 这里用了前中序遍历统一风格法.
// 核心思想: 对于一个二叉搜索树, 中序遍历后, 遍历的序列是递增的.
class Solution {public int getMinimumDifference(TreeNode root) {Stack<TreeNode> nodes = new Stack<>();TreeNode node = null;int lastNodeVal = -1;int minmumDifference = -1;nodes.push(root);while (!nodes.isEmpty()) {node = nodes.pop();if (node != null) {if (node.right != null) {nodes.push(node.right);}nodes.push(node);nodes.push(null);if (node.left != null) {nodes.push(node.left);}} else {node = nodes.pop();if (lastNodeVal != -1 && (minmumDifference == -1 || node.val - lastNodeVal < minmumDifference)) {minmumDifference = node.val - lastNodeVal;}lastNodeVal = node.val;}}return minmumDifference;}
}自己实现过程中遇到哪些困难
无
[LeetCode] 501. 二叉搜索树中的众数
[LeetCode] 501. 二叉搜索树中的众数 文章解释
[LeetCode] 501. 二叉搜索树中的众数 视频解释
题目:
给你一个含重复值的二叉搜索树(BST)的根节点
root,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
输入:root = [1,null,2,2] 输出:[2]示例 2:
输入:root = [0] 输出:[0]提示:
- 树中节点的数目在范围
[1, 104]内-105 <= Node.val <= 105进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
[LeetCode] 501. 二叉搜索树中的众数
自己看到题目的第一想法
1. 看到二叉搜索树, 第一反应就是中序是递增或者递减的.
2. 既然遍历后的序列是递增的, 那么只要拿 number 记录上一个数字, 拿 count 记录当前数字出现的次数, 同时用 maxCount 表示当前出现次数最大的数字出现的次数. 如果 count 比 maxCount 大则要清空结果列表 List<Integer> 后添加, 如果 count == maxCount, 则直接添加到结果列表 List<Integer> 中.
3. 通过中序遍历数组.
看完代码随想录之后的想法
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {private List<Integer> result = new ArrayList<>();private int maxCount = 0;private int number = 0;private int count = 0;public int[] findMode(TreeNode root) {findModeRecursion(root);int[] resultArray = new int[result.size()];for (int i = 0; i < result.size(); ++i) {resultArray[i] = result.get(i);}return resultArray;}public void findModeRecursion(TreeNode root) {if (root.left != null) {// 最早的时候这里不小心调用 findMode... 导致耗时很长findModeRecursion(root.left);}if (root.val != number) {number = root.val;count = 1;} else {count++;}if (maxCount < count) {result.clear();result.add(number);maxCount = count;} else if (maxCount == count) {result.add(number);}if (root.right != null) {// 最早的时候这里不小心调用 findMode... 导致耗时很长findModeRecursion(root.right);}}
}/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
// 迭代法
class Solution {private List<Integer> result = new ArrayList<>();private int maxCount = 0;private int number = 0;private int count = 0;public int[] findMode(TreeNode root) {if (root == null) {return new int[0];}Stack<TreeNode> nodes = new Stack<>();TreeNode node = root;while (node != null || !nodes.isEmpty()) {if (node != null) {nodes.push(node);node = node.left;} else {node = nodes.pop();if (node.val != number) {count = 1;} else {count++;}if (maxCount == count) {result.add(node.val);} else if (maxCount < count) {maxCount = count;result.clear();result.add(node.val);}number = node.val;node = node.right;}}int[] resultArray = new int[result.size()];for (int i = 0; i < result.size(); ++i) {resultArray[i] = result.get(i);}return resultArray;}
}
自己实现过程中遇到哪些困难
刚开始使用双指针的时候, 是拿当前节点和上一个节点做比较, 如果发现不想等, 才将节点添加到 List<Integer>. 一开始以为只有这样才能知道当前字符出现的次数, 以及该频率的节点是否可以添加到结果中.
这样做有一个问题就是, 如果所有数字都是相等的, 因为没有触发节点不想等的逻辑了.
后来发现不行, 于是就只能在根据当前节点的值更新完 count 后, 去判断当前节点是否要添加到结果集合中. 后来发现, 如果当前 maxCount = n, 而 当前节点的 count = n, 把当前节点添加到结果集后, 尽管下一个节点和当前节点的值是一样的, 这样说明 maxCount 要更新了, 只要清空结果集重新添加一次就可以. 完美解决...
当然, 递归方法1中, 出现了一次愚蠢的错误, 递归调用时, 调错了函数, 导致时间很长. 和随想录还有 leetcode 官方题解对了好几遍, 修改成几乎完全一样还是不对... 后来才发现调用错了函数... 所以日常没有 test case 的时候... 这样的粗心大意可是很危险的.
[LeetCode] 236. 二叉树的最近公共祖先
[LeetCode] 236. 二叉树的最近公共祖先 文章解释
[LeetCode] 236. 二叉树的最近公共祖先 视频解释
题目:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点5和节点4的最近公共祖先是节点5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1提示:
- 树中节点数目在范围
[2, 105]内。-10^9 <= Node.val <= 10^9- 所有
Node.val互不相同。p != qp和q均存在于给定的二叉树中。
[LeetCode] 236. 二叉树的最近公共祖先
自己看到题目的第一想法
第一次:
需要回溯! 回溯的模板我熟悉!
首先向左侧遍历, 当找到p或者q对应的节点后, 继续往下遍历.
于是我迷失在了节点的相互关系中.
第二次:
递归吧, 想不明白的时候递归总是能解救迷茫的算法er.
首先递归求左子树是否存在p或q, 再递归求右子树是否存在p或q.
如果左子树和右子树都返回非空, 则当前节点就是公共节点.
(提交后报错, 虽然左子树和右子树没有同时非空, 但这时候前节点是p或q中的一个, 导致返回了错误的结果)
那再加一个条件, 如果 左子树和右子树 不同时为空, 再加一个当前节点的判断, 如果匹配p或者q中的一个节点, 则返回当前节点.
(提交后报错, 因为这时候, 递归函数返回的节点, 可能只代表p或者q中的一个, 也可能代表p和q两者, 因此当 leftNode 和 rightNode 并非同时非空时, 不知道如何返回了)
那就用一个数字来计数吧, 这样就知道p和q有没有都匹配上了, 但是因为我们最终的出口只有一个节点, 因此需要在主函数中接住这个节点. 同时判断匹配的数量是否为 2. 是则返回该节点, 否则返回 Null.
至此解决问题.
第三次:
在第二次中解决问题时, 遗漏了一个问题. 那就是题目保证了p和q是一定存在的. 这会大大的简化解题的逻辑.
看完代码随想录之后的想法
因为 p 和 q 一定存在于二叉树中, 因此整体分两种情况:
1. p 和 q 分别位于某个节点的左右子树中
2. p 和 q 中有一个是公共节点
因此, 当我们匹配到 p 或者 q 中的一个节点时, 就可以直接返回, 以该节点为根节点的子树可以不用考虑了. 因为如果该节点是公共子节点的孩子节点的话, 那另外一个就在父节点的另外一个子树中, 可以被遍历到. 或者不在该节点的父节点的另一个子树中, 而是在祖先结点的另一个子树中, 因此也可以被遍历到. 如果在其他地方找不到另外一个待匹配的节点的话, 那自然说明该节点的子节点中, 一定右另外一个可以匹配的 p 或者 q 节点.
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
// 自己的解法: 后序遍历, 不需要p和q同时存在(未验证)
class Solution {private TreeNode result = null;private int matchCount = 0;public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {TreeNode node = findNode(root, p, q);if (node != null && matchCount == 2) {return node;}return null;}private TreeNode findNode(TreeNode root, TreeNode p, TreeNode q) {if (root == null) {return null;}TreeNode leftNode = null;TreeNode rightNode = null;leftNode = findNode(root.left, p, q);rightNode = findNode(root.right, p, q);if (leftNode != null && rightNode != null) {return root;} else {if (root.val == q.val || root.val == p.val) {matchCount++;return root;}if (leftNode != null) {return leftNode;} else if (rightNode != null) {return rightNode;}}return null;}
}/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
// 后序遍历: 假设 p 和 q 一定存在
class Solution {private TreeNode result = null;private int matchCount = 0;public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == null) {return null;}TreeNode leftNode = lowestCommonAncestor(root.left, p, q);TreeNode rightNode = lowestCommonAncestor(root.right, p, q);if (leftNode != null && rightNode != null) {return root;}if (root.val == p.val || root.val == q.val) {return root;} else if (leftNode != null) {return leftNode;} else {return rightNode;}}
}自己实现过程中遇到哪些困难
当处理了 p 和 q 分别位于公共节点的左右子树时, p 和 q 同时位于公共节点同一侧子树的情况就无法满足. 虽然看似就那么几个判断条件, 但真正实现起来似乎怎么也绕不出来. 不过最后还是做出来了... 就是耗费的时间也真的很长. 在这一题上稍微有点沮丧.
相关文章:

代码随想录算法训练营第二十一天| 530. 二叉搜索树的最小绝对差、501. 二叉搜索树中的众数、236. 二叉树的最近公共祖先
[LeetCode] 530. 二叉搜索树的最小绝对差 [LeetCode] 530. 二叉搜索树的最小绝对差 文章解释 [LeetCode] 530. 二叉搜索树的最小绝对差 视频解释 题目: 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其…...

【面试】JDK和JVM是什么关系?
目录 1. JDK2. JVM3. 关系 1. JDK 1.Java Development Kit,java开发工具包。2.提供了java应用程序开发所需的所有工具和API。3.JDK包含了JRE(Java Runtime Environment),即Java运行环境,以及编译Java源代码的编译器(j…...
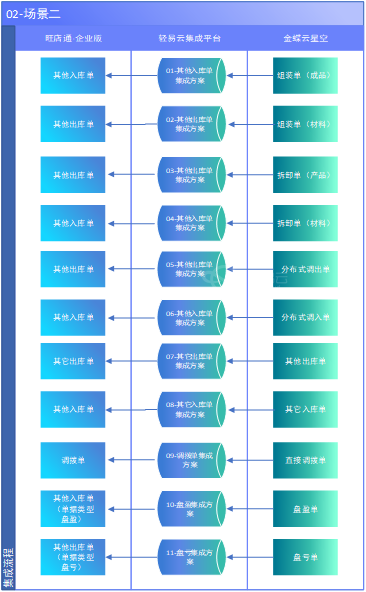
旺店通与金蝶云星空 就应该这样集成打通
在当今数字化商业环境中,企业需要高效、灵活的系统来支持其业务运营。旺店通和金蝶云星空作为两个领先的企业管理解决方案,它们的集成能够为企业带来无缝的业务流程和数据一致性。本文将详细介绍旺店通与金蝶云星空的全场景集成方案,包括主数…...
linux开发之设备树
设备树的基本概念 1.什么是设备树?为什么叫设备树呢? 设备树是描述硬件的文本文件,因为语法结构像树一样。所以叫设备树。 2.基本名词解释 <1>DT:Device Tree //设备树 <2>FDT:Flattened Device Tree //开放设备树,起源于0penFirmware(0F…...

DQL(数据查询)
目录 1. DQL概念 2. DQL - 编写顺序 3. 基础查询 3.1 查询多个字段 3.2 字段设置别名 3.3 去除重复记录 3.4 案例 4. 条件查询 4.1 语法 4.2 条件 4.3 案例: 5. 聚合函数 5.1 常见的聚合函数: 5.2 语法 5.3 案例: 6. 分组查…...
)
LeetCode 2951.找出峰值:模拟(遍历)
【LetMeFly】2951.找出峰值:模拟(遍历) 力扣题目链接:https://leetcode.cn/problems/find-the-peaks/ 给你一个下标从 0 开始的数组 mountain 。你的任务是找出数组 mountain 中的所有 峰值。 以数组形式返回给定数组中 峰值 的…...

软考结束。有什么要说的
1. 竟然是机试,出乎我意料。是 考试机构觉得笔试成本高了么。这次的考试是机试,相比以往有所不一样。感言是不是以后都会在固定地点考试也说不准。 2. 遇到年轻人。 这次旁边的一个女同学第一次参加,还像我询问了一些关于软考的事。我是有…...
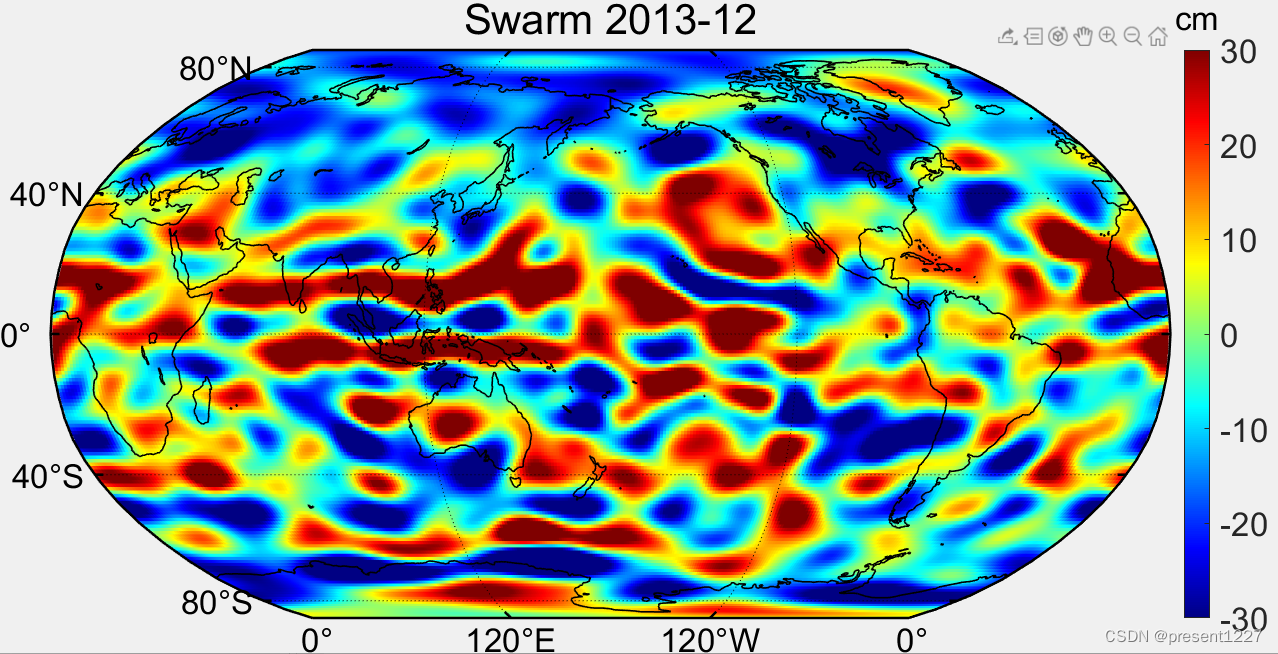
Matlab读取Swarm球谐系数,并绘制EWH全球格网图(存在疑问)
ICGEM官网下载 COST-G发布的4040的球谐系数 close all; clearvars -except; % addpath(E:\Code\Tool\Function\GRACE_functions); dir_degree_1 E:\Code\GRACE_data\Degree_1\deg1_coef.txt; dir_c20 E:\Code\GRACE_data\Degree_2\C20_RL06.txt; myDir_Swarm E:…...

Vue集成Iframe
一、应用场景,为什么要集成Iframe? 1、庞大项目拆分后,便于管理和部署,用集成Iframe的方法合并 2、避免功能重复开发,共用模块可单独开发为一个项目,既可独立部署,也可集成到中台系统 二、集成…...
Android Studio 所有历史版本下载
一、官网链接 https://developer.android.google.cn/studio/archive 操作 二、AndroidDevTools地址 https://www.androiddevtools.cn/ 参考 https://blog.csdn.net/qq_27623455/article/details/103008937...
5.27作业
定义自己的命名空间my_sapce,在my_sapce中定义string类型的变量s1,再定义一个函数完成对字符串的逆置。 #include <iostream> #include <string.h>using namespace std; namespace my_space {string s1;void RevString(string &s1); } v…...

微服务架构下的‘黑带’安全大师:Spring Cloud Security全攻略!
深入探讨了微服务间的安全通信、安全策略设计以及面对经典安全问题的应对策略。无论你是微服务的新手还是资深开发者,都能在本文中找到提升安全功力的秘籍。让我们一起成为微服务架构下的‘黑带’安全大师! 文章目录 1. 引言微服务安全挑战与重要性Sprin…...

Py列表(list)
目录 正向索引: 反向索引: 嵌套列表: 修改列表中的值 列表常用的方法 实例 练习: 正向索引: 从0开始,依次递增。第一个元素的索引为0,第二个元素的索引为1,依此类推。 列表的下标…...
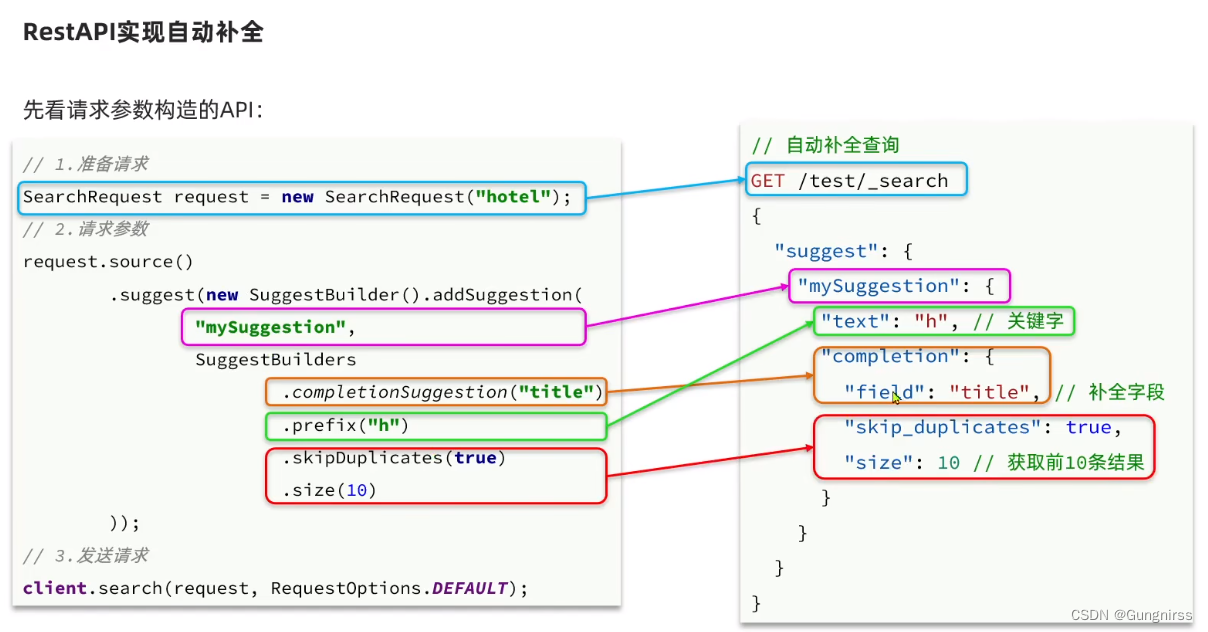
黑马es0-1实现自动补全功能
1、安装分词器 上github上找人做好的分词器,放到es-plugin数据卷里,然后重启es即可 2、自定义分词器 elasticsearch中分词器(analyzer)的组成包含三部分: character filters:在tokenizer之前对文本进行处理。例如删除字符、替换字符 …...

react通过上下文深入传递数据
通常,您将通过 props 将信息从父组件传递到子组件。但是,如果必须将道具传递到中间的许多组件,或者应用中的许多组件需要相同的信息,则传递道具可能会变得冗长且不方便。Context 允许父组件将一些信息提供给其下树中的任何组件&am…...

「代码厨房大揭秘:Python性能优化的烹饪秘籍!」
哈喽,我是阿佑,上篇咱们讲了 Socket 编程 —— 探索Python Socket编程,赋予你的网络应用隐形斗篷般的超能力!从基础到实战,构建安全的聊天室和HTTP服务器,成为网络世界的守护者。加入我们,一起揭…...

【重学C语言】十六、联合、枚举、面向对象编程
【重学C语言】十六、联合、枚举、面向对象编程 联合定义联合体使用联合体注意事项枚举枚举的定义为枚举常量指定整数值枚举的使用枚举的打印枚举的优势注意事项面向对象编程1. 结构体(Structs)2. 封装(Encapsulation)3. 继承(Inheritance)...

Github2024-05-21 Python开源项目日报 Top10
根据Github Trendings的统计,今日(2024-05-21统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目10C项目1TypeScript项目1youtube-dl - 从YouTube和其他网站下载视频的命令行程序 创建周期:4951 天开发语言:Python协议类型:The …...
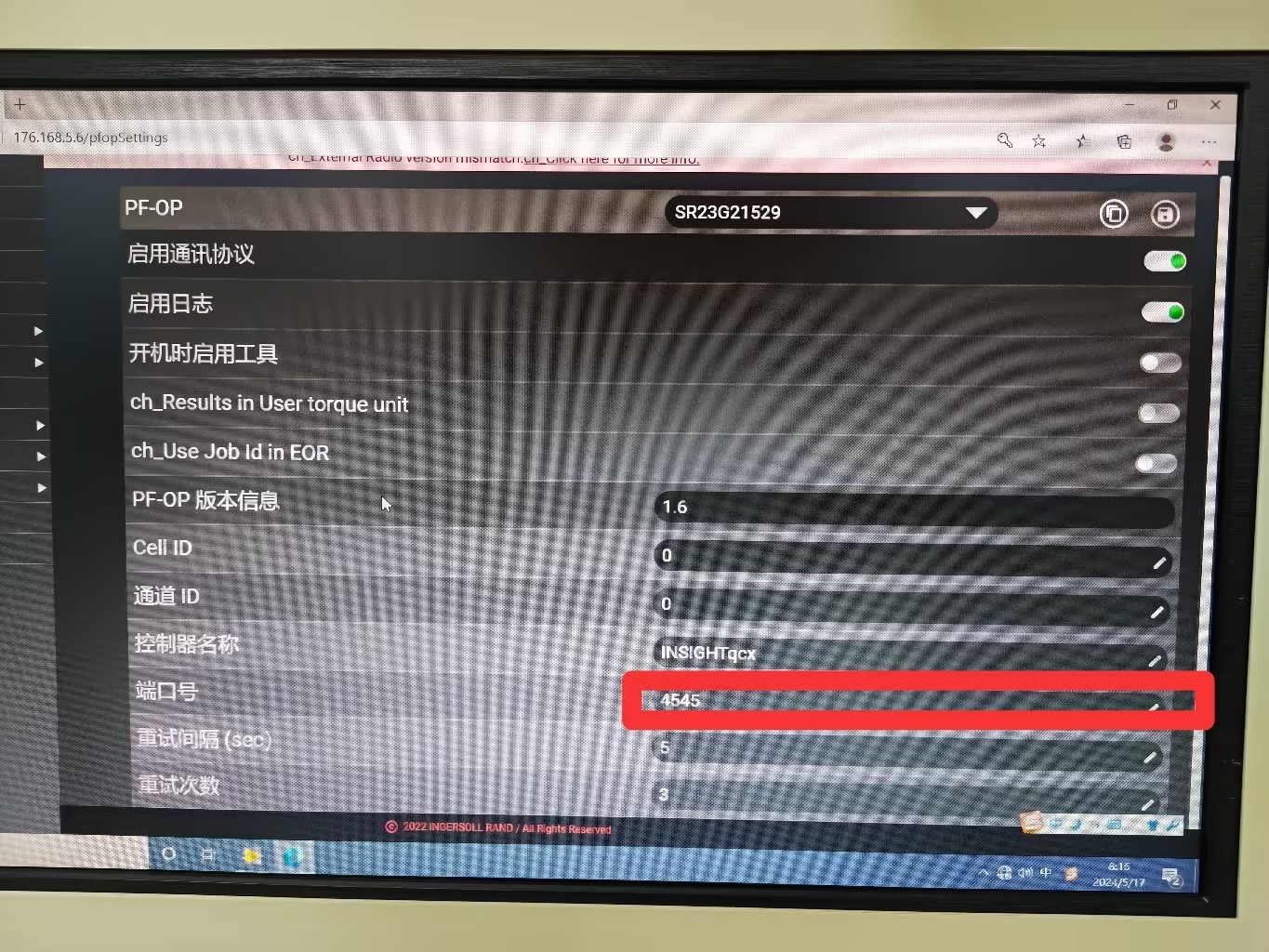
labview_开放协议
一、开放协议 二、硬件设置 英格索兰硬件设置: 三、配套测试软件 四、Labview代码...

AWS安全性身份和合规性之Amazon Macie
Amazon Macie是一项数据安全和数据隐私服务,它利用机器学习(ML)和模式匹配来发现和保护敏感数据。可帮助客户发现、分类和保护其敏感数据,以及监控其数据存储库的安全性。 应用场景: 敏感数据发现 一家金融服务公司…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
