代码随想录算法训练营第四十一天| 509. 斐波那契数 、70. 爬楼梯 、746. 使用最小花费爬楼梯
509. 斐波那契数
题目链接:509. 斐波那契数
文档讲解:代码随想录/斐波那契数
视频讲解:视频讲解-斐波那契数
状态:已完成(1遍)
解题过程
看到题目的第一想法
虽然看了卡哥的动态规划五部曲,但是看到题目之后还是不太会操作索性不要有自己多余的思考了,直接看视频讲解。
看完代码随想录之后的想法
用动态规划五部曲:
- 确定dp数组以及下标的含义:dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 确定递推公式:dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化:dp[0] = 0 、dp[1] = 1;
- 确定遍历顺序:从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的;
- 举例推导dp数组:
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:0 1 1 2 3 5 8 13 21 34 55。
看了讲解手搓代码如下:
/*** @param {number} n* @return {number}*/
var fib = function(n) {let dp = [];dp[0] = 0,dp[1] = 1;for(let i = 2;i<=n;i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];
};总结
这道题作为动态规划之所以简单,是因为递推公式、初始化、遍历顺序都已经由题目确定。
70. 爬楼梯
题目链接:70. 爬楼梯
文档讲解:代码随想录/爬楼梯
视频讲解:视频讲解-爬楼梯
状态:已完成(1遍)
解题过程
看到题目的第一想法
用动态规划五部曲:
- 确定dp数组以及下标的含义:dp[i]的定义为:到第i层阶梯有dp[i]种方式能够来到;
- 确定递推公式:dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化:dp[0] = 1 、dp[1] = 1、dp[2] = 2;
- 确定遍历顺序:从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的;
- 举例推导dp数组:
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,dp数组应该是如下的数列: 1 1 2 3 5 8 13 21 34 55。
手搓代码如下:
/*** @param {number} n* @return {number}*/
var climbStairs = function(n) {let dp = [1,1];for(let i =2;i<=n;i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];
};提交成功!
看完代码随想录之后的想法
严格遵守对dp[i]的描述,直接没有i=0的时候。
讲解代码如下:
/*** @param {number} n* @return {number}*/
var climbStairs = function(n) {// dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶// dp[i] = dp[i - 1] + dp[i - 2]let dp = [1 , 2]for(let i = 2; i < n; i++) {dp[i] = dp[i - 1] + dp[i - 2]}return dp[n - 1]
};总结
一开始我就往动态规划的思路上靠,感觉既然只有两种行走方式,那到dp[i]级阶梯的方式肯定就是他的下一级dp[i-1]和下两级dp[i-2],所以到这级阶梯的方式就是到下两级阶梯方式的和。
746. 使用最小花费爬楼梯
题目链接:746. 使用最小花费爬楼梯
文档讲解:代码随想录/使用最小花费爬楼梯
视频讲解:视频讲解-使用最小花费爬楼梯
状态:已完成(1遍)
解题过程
看到题目的第一想法
用动态规划五部曲:
- 确定dp数组以及下标的含义:dp[i]的定义为:从第i层阶梯出发的最小花费dp[i]元;
- 确定递推公式:dp[i] = dp[i - 1] 和 dp[i - 2] 的最小值 + cost[i];
- dp数组如何初始化:dp[0] = cost[0] 、dp[1] =cost[1] ;
- 确定遍历顺序:从递归公式中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的;
- 举例推导dp数组:
按照这个递推公式我们来推导一下,dp数组应该是如下的数列: 10 15 30 。
手搓代码如下:
/*** @param {number[]} cost* @return {number}*/
var minCostClimbingStairs = function(cost) {let dp = [cost[0],cost[1]];for(let i =2;i<cost.length;i++){dp[i] = Math.min(dp[i - 1],dp[i - 2]) + cost[i];}return Math.min(dp[cost.length-1],dp[cost.length-2]);
};提交成功,没有问题。 我在求最后一级阶梯的时候就不用走for循环里了,直接比较从前两节阶梯哪个出发更便宜。
看完代码随想录之后的想法
卡尔哥用dp[i]表示到达第i节阶梯的最便宜花费,确实省事一点。
讲解代码如下:
/*** @param {number[]} cost* @return {number}*/
var minCostClimbingStairs = function(cost) {const dp = [0, 0]for (let i = 2; i <= cost.length; ++i) {dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])}return dp[cost.length]
};总结
今天的三道题还算简单,希望明后天可以撑住。
相关文章:

代码随想录算法训练营第四十一天| 509. 斐波那契数 、70. 爬楼梯 、746. 使用最小花费爬楼梯
509. 斐波那契数 题目链接:509. 斐波那契数 文档讲解:代码随想录/斐波那契数 视频讲解:视频讲解-斐波那契数 状态:已完成(1遍) 解题过程 看到题目的第一想法 虽然看了卡哥的动态规划五部曲,…...
Ribbon负载均衡(自己总结的)
文章目录 Ribbon负载均衡负载均衡解决的问题不要把Ribbon负载均衡和Eureka-Server服务器集群搞混了Ribbon负载均衡代码怎么写ribbon负载均衡依赖是怎么引入的? Ribbon负载均衡 负载均衡解决的问题 首先Ribbon负载均衡配合Eureka注册中心一块使用。 在SpringCloud…...

Leetcode 力扣92. 反转链表 II (抖音号:708231408)
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出:[1,4,3,2…...

OSI七层模型和TCP/IP四层模型的区别
OSI七层模型 1.物理层(Physical Layer) 实现相邻节点之间比特流的透明传输,尽可能屏蔽传输介质带来的差异。典型设备:集线器(Hub)。 2.数据链路层(Data Link Layer) 将网络层传下来…...

在虚拟机上安装MySQL和Hive
在虚拟机上安装MySQL和Hive的步骤如下。这里将分别针对MySQL和Hive的安装进行说明。 MySQL安装步骤 1. 准备工作 下载MySQL安装包,选择与你虚拟机操作系统版本相匹配的MySQL版本,例如MySQL 8.0.35。 2. 卸载旧版本(如果已安装)…...

Vue 2 和 Vue 3 中同步和异步
Vue 2 和 Vue 3 中同步和异步 Vue 2 同步和异步 同步更新 (Synchronous Updates) Vue 2 在数据更新后会进行同步渲染更新,但为了性能优化,Vue 会在内部队列中异步地进行 DOM 更新。这意味着数据变化会立即被捕捉到,但实际的 DOM 更新会被推迟到下一个事件循环队列中。new V…...
ssm150旅游网站的设计与实现+jsp
旅游网站设计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本旅游网站就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理完毕庞…...

【加密与解密(第四版)】第十四章笔记
第十四章 漏洞分析技术 14.1 软件漏洞原理 缓冲区溢出漏洞:栈溢出 堆溢出、整型溢出(存储溢出、计算溢出、符号问题) UAF(Use-After-Free)漏洞 14.2 ShellCode 功能模块:下载执行、捆绑、反弹shell 14.3 …...
鸿蒙系统和安卓系统通过termux搭建Linux系统—Centos
目录 1. 前言 2. 效果图展示 3. 安装termux 4. 安装Centos系统 4.1 更换源 4.2 拉取镜像 4.3 启动centos 5.结尾 1. 前言 大家好,我是jiaoxingk 今天这篇文章让你能够在手机或者平板上使用Linux-Centos系统 让你随时随地都能操作命令行进行装13 2. 效果图展示…...
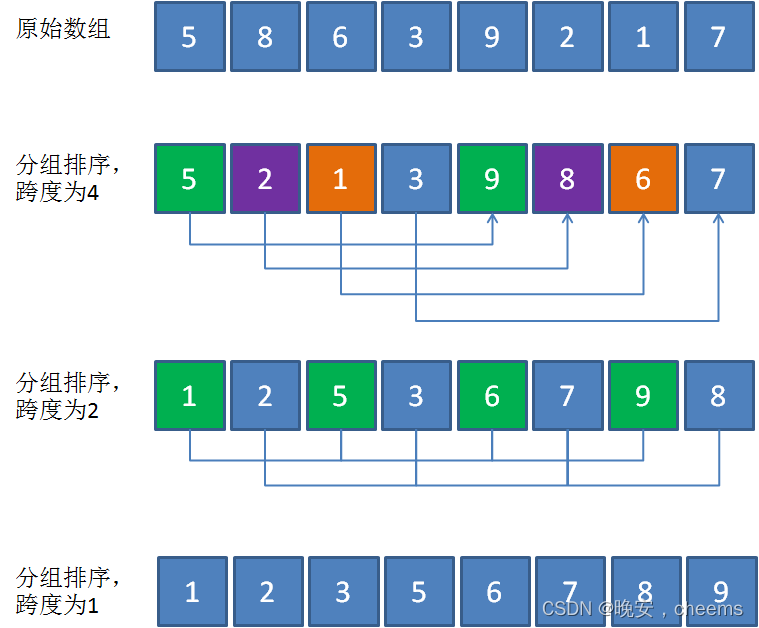
数据结构的希尔排序(c语言版)
一.希尔排序的概念 1.希尔排序的基本思想 希尔排序是一种基于插入排序算法的优化排序方法。它的基本思想如下: 选择一个增量序列 t1,t2,......,tk,其中 ti > tj, 当 i < j,并且 tk 1。 按增量序列个数k&#…...

使用Node.js搭建服务器
使用Node.js搭建服务器 1.安装Node.js和npm 安装教程自行搜索(好多),建议Node.js直接安装在C盘 注意镜像的设置:npm install -g cnpm --registryhttps://registry.npm.taobao.org 注意版本检查: //以下是我使用的版…...

网络编程——多进程的服务器
多进程的网络服务器 多进程的网络服务器是一种使用多个进程来处理并发网络请求的服务器架构。在这种架构中,服务器在接收到客户端连接请求后,会创建一个新的子进程来处理该请求,从而允许服务器同时处理多个客户端连接。多进程服务器通常用于…...

代码随想录算法训练营第二十一天| 530. 二叉搜索树的最小绝对差、501. 二叉搜索树中的众数、236. 二叉树的最近公共祖先
[LeetCode] 530. 二叉搜索树的最小绝对差 [LeetCode] 530. 二叉搜索树的最小绝对差 文章解释 [LeetCode] 530. 二叉搜索树的最小绝对差 视频解释 题目: 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其…...

【面试】JDK和JVM是什么关系?
目录 1. JDK2. JVM3. 关系 1. JDK 1.Java Development Kit,java开发工具包。2.提供了java应用程序开发所需的所有工具和API。3.JDK包含了JRE(Java Runtime Environment),即Java运行环境,以及编译Java源代码的编译器(j…...
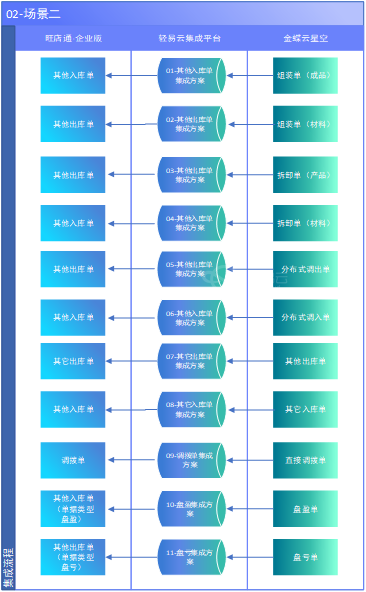
旺店通与金蝶云星空 就应该这样集成打通
在当今数字化商业环境中,企业需要高效、灵活的系统来支持其业务运营。旺店通和金蝶云星空作为两个领先的企业管理解决方案,它们的集成能够为企业带来无缝的业务流程和数据一致性。本文将详细介绍旺店通与金蝶云星空的全场景集成方案,包括主数…...
linux开发之设备树
设备树的基本概念 1.什么是设备树?为什么叫设备树呢? 设备树是描述硬件的文本文件,因为语法结构像树一样。所以叫设备树。 2.基本名词解释 <1>DT:Device Tree //设备树 <2>FDT:Flattened Device Tree //开放设备树,起源于0penFirmware(0F…...

DQL(数据查询)
目录 1. DQL概念 2. DQL - 编写顺序 3. 基础查询 3.1 查询多个字段 3.2 字段设置别名 3.3 去除重复记录 3.4 案例 4. 条件查询 4.1 语法 4.2 条件 4.3 案例: 5. 聚合函数 5.1 常见的聚合函数: 5.2 语法 5.3 案例: 6. 分组查…...
)
LeetCode 2951.找出峰值:模拟(遍历)
【LetMeFly】2951.找出峰值:模拟(遍历) 力扣题目链接:https://leetcode.cn/problems/find-the-peaks/ 给你一个下标从 0 开始的数组 mountain 。你的任务是找出数组 mountain 中的所有 峰值。 以数组形式返回给定数组中 峰值 的…...

软考结束。有什么要说的
1. 竟然是机试,出乎我意料。是 考试机构觉得笔试成本高了么。这次的考试是机试,相比以往有所不一样。感言是不是以后都会在固定地点考试也说不准。 2. 遇到年轻人。 这次旁边的一个女同学第一次参加,还像我询问了一些关于软考的事。我是有…...
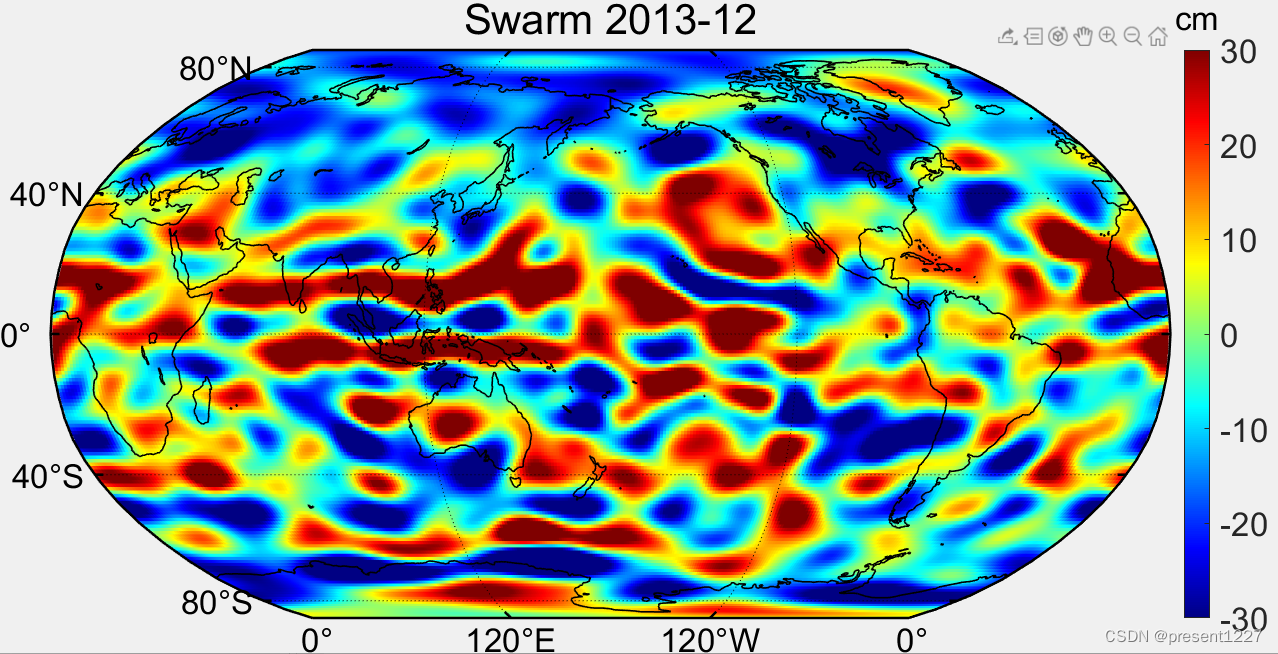
Matlab读取Swarm球谐系数,并绘制EWH全球格网图(存在疑问)
ICGEM官网下载 COST-G发布的4040的球谐系数 close all; clearvars -except; % addpath(E:\Code\Tool\Function\GRACE_functions); dir_degree_1 E:\Code\GRACE_data\Degree_1\deg1_coef.txt; dir_c20 E:\Code\GRACE_data\Degree_2\C20_RL06.txt; myDir_Swarm E:…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
