数据结构的希尔排序(c语言版)
一.希尔排序的概念
1.希尔排序的基本思想
希尔排序是一种基于插入排序算法的优化排序方法。它的基本思想如下:
-
选择一个增量序列 t1,t2,......,tk,其中 ti > tj, 当 i < j,并且 tk = 1。
-
按增量序列个数k,对数组进行k趟排序:
- 第一趟,按 t1 的增量对数组进行插入排序;
- 第二趟,按 t2 的增量对数组进行插入排序;
- ... ...
- 第k趟,按 tk 的增量(此时 tk = 1),也就是对整个数组进行插入排序。
2.希尔排序的优点
-
时间复杂度较低。希尔排序的时间复杂度一般在 O(n^1.25) 和 O(n^1.5) 之间,优于简单的插入排序。
-
在部分有序的数组中效率很高。希尔排序通过分组插入排序来利用数据的局部有序性,可以有效地加快排序速度。
-
空间复杂度低,只需要常量级的额外空间。
-
代码实现相对简单,易于理解和编码。
3.希尔排序的缺点
-
增量序列的选择对排序效率有很大影响。不同的增量序列会导致很大的性能差异。找到最优的增量序列是一个难题。
-
在数据量很大时,性能可能不如其他算法,如快速排序、堆排序等。
-
不稳定。希尔排序是不稳定的排序算法,即相等的元素可能会改变相对次序。
-
理论分析复杂。希尔排序的时间复杂度分析比较困难,没有得到一个统一的结论。
4.希尔排序与快速排序在使用情况时的差异
-
数据量中等且部分有序:
- 希尔排序通过分组排序利用了数据的局部有序性,在部分有序的数组上表现很好。
- 而快速排序在部分有序数组上可能会退化为 O(n^2) 的时间复杂度。
-
内存受限的环境:
- 希尔排序只需要常量级的额外空间,而快速排序需要递归调用栈,在内存受限的环境下可能会有优势。
-
数据分布不均匀:
- 快速排序的性能很容易受到数据分布的影响,而希尔排序相对更加好。
-
预先知道数据大致分布情况:
- 如果对数据的分布有一定了解,可以选择合适的增量序列来优化希尔排序的性能。
-
对稳定性要求不高:
- 快速排序是不稳定的,而希尔排序也是不稳定的。如果稳定性不是关键,希尔排序可能是更好的选择。
二.希尔排序的功能
1.分组插入排序
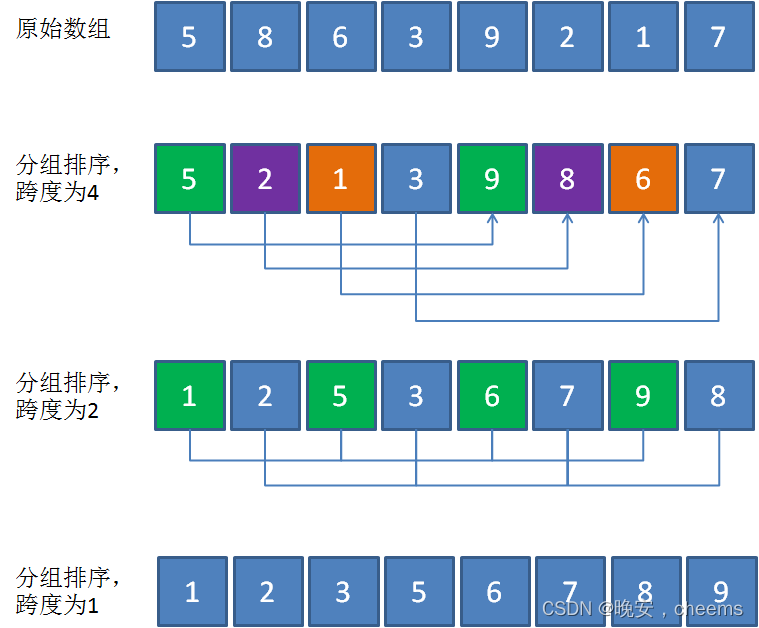
- 希尔排序的核心思想是通过分组插入排序来优化基本的插入排序算法。
- 它首先选择一个增量序列,如
[n/2, n/4, n/8, ...],将原始数组划分为多个子数组。 - 每个子数组的元素索引差为增量值。例如,当增量为 4 时,子数组为
arr[0]、arr[4]、arr[8]...。 - 对这些子数组分别进行插入排序。
- 随着增量序列逐步减小,子数组中的元素越来越集中,最终整个数组被完全排序。
2.利用局部有序性
- 在初始阶段,当增量较大时,子数组中的元素较为分散。
- 随着增量的不断减小,子数组中的元素逐渐趋于有序。
- 这种分组插入排序可以有效利用数据的局部有序性,从而减少插入排序的比较和移动操作次数。
3.时间复杂度优化
- 基本插入排序的时间复杂度为 O(n^2)。
- 而希尔排序通过分组插入排序和利用局部有序性,可以将平均时间复杂度优化到 O(n^1.25) 到 O(n^1.5)。
4.空间复杂度低
- 希尔排序只需要常量级的额外空间来存储一些中间变量,如增量序列等。
- 因此它的空间复杂度很低,仅为 O(1)。
5.代码实现简单
- 与其他高效排序算法相比,如快速排序和归并排序,希尔排序的代码实现较为简单。
- 它只需要一个嵌套循环来完成分组和插入排序即可。
三.希尔排序的代码实现
1.排序的实现
-
定义一个名为
shell_sort的函数,它接受两个参数:arr: 一个整型数组,需要被排序n: 数组的长度
-
shell_sort函数的实现:- 使用一个
for循环来遍历不同的增量值gap。初始的gap为n/2。 - 对于每个
gap值,我们再次使用一个for循环来遍历数组。 - 对于每个元素
arr[i],我们将其暂存到临时变量temp中。 - 然后,我们使用另一个内层
for循环来执行分组插入排序。在这个循环中,我们将arr[j]的值移动到arr[j - gap]的位置,直到找到temp应该插入的位置。 - 最后,我们将
temp赋值给arr[j]。 - 重复上述过程,直到
gap变为 0。
- 使用一个
void shell_sort(int arr[], int n) {for (int gap = n / 2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = arr[i];int j;for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}
}2.main函数
- 定义一个示例数组
arr。 - 计算数组长度
n。 - 打印出未排序的数组。
- 调用
shell_sort函数对数组进行排序。 - 打印出排序后的数组。
int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr) / sizeof(arr[0]);printf("Unsorted array: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");shell_sort(arr, n);printf("Sorted array: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}3.程序的执行流程
- 首先,在
main函数中,我们定义了一个示例数组arr。 - 然后,我们计算数组的长度
n。 - 接下来,我们打印出未排序的数组。
- 调用
shell_sort函数对数组进行排序。 - 在
shell_sort函数内部,我们使用一个for循环来迭代不同的增量值gap。初始的gap为n/2。 - 对于每个
gap值,我们遍历数组,对于每个元素arr[i],我们将其暂存到临时变量temp中。 - 然后,我们使用另一个内层
for循环来执行分组插入排序。在这个循环中,我们将arr[j]的值移动到arr[j - gap]的位置,直到找到temp应该插入的位置。 - 最后,我们将
temp赋值给arr[j]。 - 重复上述过程,直到
gap变为 0。 - 排序完成后,我们在
main函数中打印出排序后的数组。
四.希尔排序的源代码
- 首先,我们定义一个
shell_sort函数,接受一个整型数组arr和数组长度n作为参数。 - 在函数内部,我们使用一个
for循环来迭代不同的增量值gap。初始的gap为n/2。 - 对于每个
gap值,我们遍历数组,对于每个元素arr[i],我们将其暂存到临时变量temp中。 - 然后,我们使用另一个内层
for循环来执行分组插入排序。在这个循环中,我们将arr[j]的值移动到arr[j - gap]的位置,直到找到temp应该插入的位置。 - 最后,我们将
temp赋值给arr[j]。 - 重复上述过程,直到
gap变为 0。
#include <stdio.h>void shell_sort(int arr[], int n) {for (int gap = n / 2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = arr[i];int j;for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}
}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr) / sizeof(arr[0]);printf("Unsorted array: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");shell_sort(arr, n);printf("Sorted array: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}相关文章:

数据结构的希尔排序(c语言版)
一.希尔排序的概念 1.希尔排序的基本思想 希尔排序是一种基于插入排序算法的优化排序方法。它的基本思想如下: 选择一个增量序列 t1,t2,......,tk,其中 ti > tj, 当 i < j,并且 tk 1。 按增量序列个数k&#…...

使用Node.js搭建服务器
使用Node.js搭建服务器 1.安装Node.js和npm 安装教程自行搜索(好多),建议Node.js直接安装在C盘 注意镜像的设置:npm install -g cnpm --registryhttps://registry.npm.taobao.org 注意版本检查: //以下是我使用的版…...

网络编程——多进程的服务器
多进程的网络服务器 多进程的网络服务器是一种使用多个进程来处理并发网络请求的服务器架构。在这种架构中,服务器在接收到客户端连接请求后,会创建一个新的子进程来处理该请求,从而允许服务器同时处理多个客户端连接。多进程服务器通常用于…...

代码随想录算法训练营第二十一天| 530. 二叉搜索树的最小绝对差、501. 二叉搜索树中的众数、236. 二叉树的最近公共祖先
[LeetCode] 530. 二叉搜索树的最小绝对差 [LeetCode] 530. 二叉搜索树的最小绝对差 文章解释 [LeetCode] 530. 二叉搜索树的最小绝对差 视频解释 题目: 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其…...

【面试】JDK和JVM是什么关系?
目录 1. JDK2. JVM3. 关系 1. JDK 1.Java Development Kit,java开发工具包。2.提供了java应用程序开发所需的所有工具和API。3.JDK包含了JRE(Java Runtime Environment),即Java运行环境,以及编译Java源代码的编译器(j…...
旺店通与金蝶云星空 就应该这样集成打通
在当今数字化商业环境中,企业需要高效、灵活的系统来支持其业务运营。旺店通和金蝶云星空作为两个领先的企业管理解决方案,它们的集成能够为企业带来无缝的业务流程和数据一致性。本文将详细介绍旺店通与金蝶云星空的全场景集成方案,包括主数…...
linux开发之设备树
设备树的基本概念 1.什么是设备树?为什么叫设备树呢? 设备树是描述硬件的文本文件,因为语法结构像树一样。所以叫设备树。 2.基本名词解释 <1>DT:Device Tree //设备树 <2>FDT:Flattened Device Tree //开放设备树,起源于0penFirmware(0F…...

DQL(数据查询)
目录 1. DQL概念 2. DQL - 编写顺序 3. 基础查询 3.1 查询多个字段 3.2 字段设置别名 3.3 去除重复记录 3.4 案例 4. 条件查询 4.1 语法 4.2 条件 4.3 案例: 5. 聚合函数 5.1 常见的聚合函数: 5.2 语法 5.3 案例: 6. 分组查…...
)
LeetCode 2951.找出峰值:模拟(遍历)
【LetMeFly】2951.找出峰值:模拟(遍历) 力扣题目链接:https://leetcode.cn/problems/find-the-peaks/ 给你一个下标从 0 开始的数组 mountain 。你的任务是找出数组 mountain 中的所有 峰值。 以数组形式返回给定数组中 峰值 的…...

软考结束。有什么要说的
1. 竟然是机试,出乎我意料。是 考试机构觉得笔试成本高了么。这次的考试是机试,相比以往有所不一样。感言是不是以后都会在固定地点考试也说不准。 2. 遇到年轻人。 这次旁边的一个女同学第一次参加,还像我询问了一些关于软考的事。我是有…...
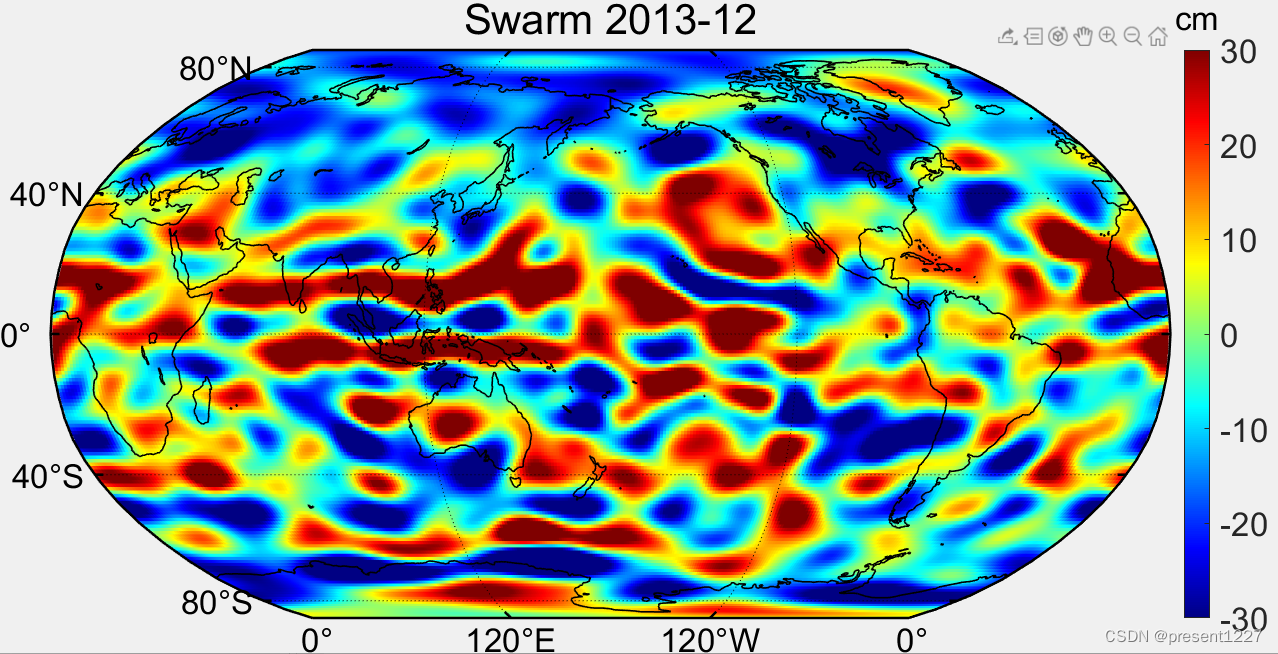
Matlab读取Swarm球谐系数,并绘制EWH全球格网图(存在疑问)
ICGEM官网下载 COST-G发布的4040的球谐系数 close all; clearvars -except; % addpath(E:\Code\Tool\Function\GRACE_functions); dir_degree_1 E:\Code\GRACE_data\Degree_1\deg1_coef.txt; dir_c20 E:\Code\GRACE_data\Degree_2\C20_RL06.txt; myDir_Swarm E:…...

Vue集成Iframe
一、应用场景,为什么要集成Iframe? 1、庞大项目拆分后,便于管理和部署,用集成Iframe的方法合并 2、避免功能重复开发,共用模块可单独开发为一个项目,既可独立部署,也可集成到中台系统 二、集成…...
Android Studio 所有历史版本下载
一、官网链接 https://developer.android.google.cn/studio/archive 操作 二、AndroidDevTools地址 https://www.androiddevtools.cn/ 参考 https://blog.csdn.net/qq_27623455/article/details/103008937...
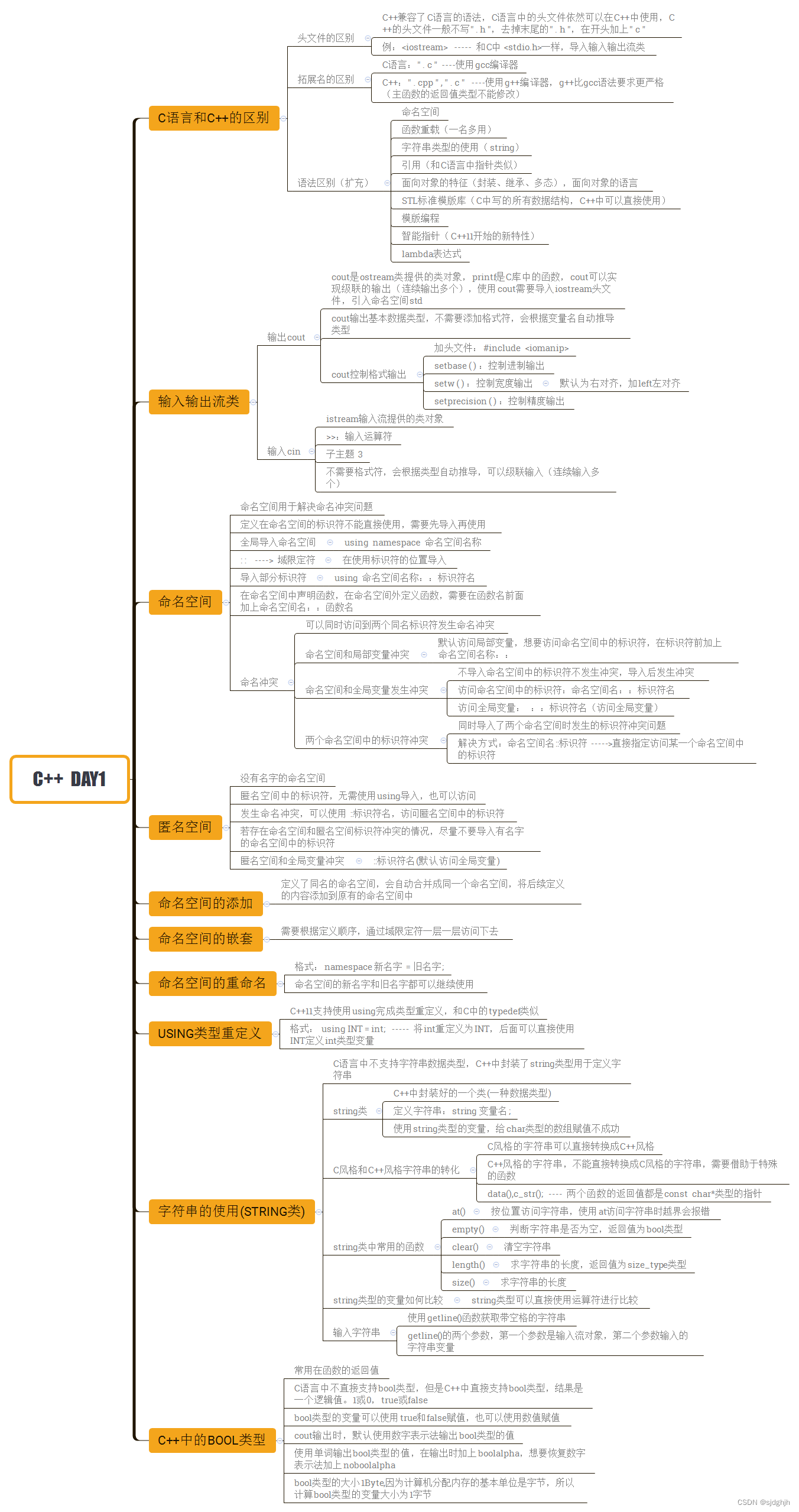
5.27作业
定义自己的命名空间my_sapce,在my_sapce中定义string类型的变量s1,再定义一个函数完成对字符串的逆置。 #include <iostream> #include <string.h>using namespace std; namespace my_space {string s1;void RevString(string &s1); } v…...

微服务架构下的‘黑带’安全大师:Spring Cloud Security全攻略!
深入探讨了微服务间的安全通信、安全策略设计以及面对经典安全问题的应对策略。无论你是微服务的新手还是资深开发者,都能在本文中找到提升安全功力的秘籍。让我们一起成为微服务架构下的‘黑带’安全大师! 文章目录 1. 引言微服务安全挑战与重要性Sprin…...

Py列表(list)
目录 正向索引: 反向索引: 嵌套列表: 修改列表中的值 列表常用的方法 实例 练习: 正向索引: 从0开始,依次递增。第一个元素的索引为0,第二个元素的索引为1,依此类推。 列表的下标…...
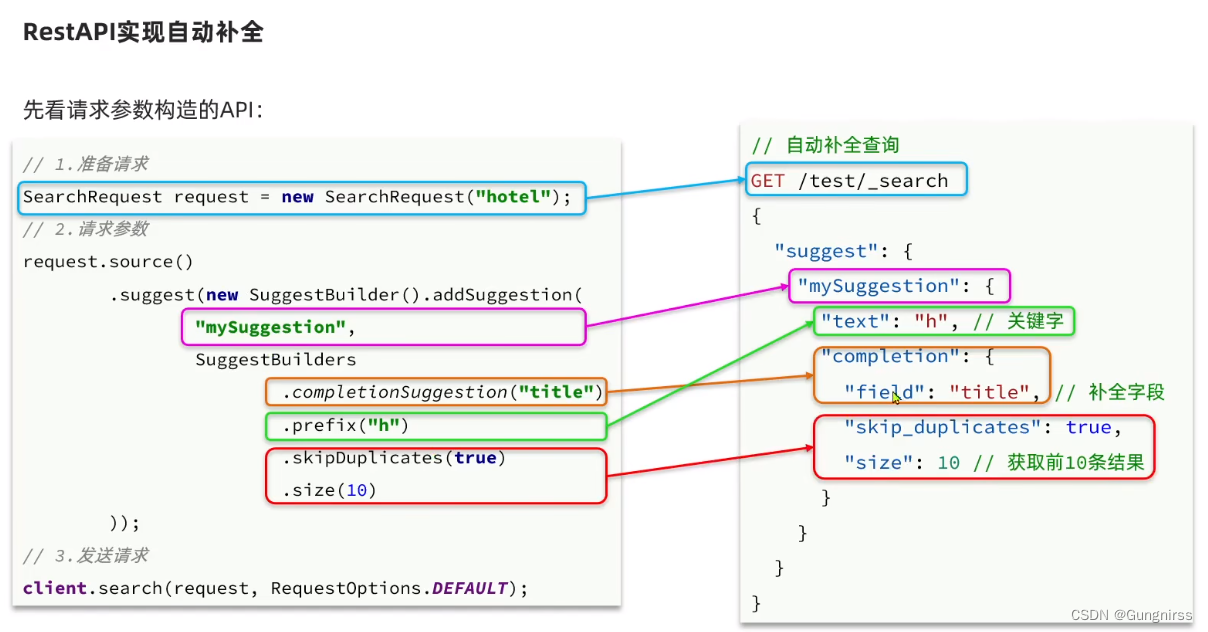
黑马es0-1实现自动补全功能
1、安装分词器 上github上找人做好的分词器,放到es-plugin数据卷里,然后重启es即可 2、自定义分词器 elasticsearch中分词器(analyzer)的组成包含三部分: character filters:在tokenizer之前对文本进行处理。例如删除字符、替换字符 …...

react通过上下文深入传递数据
通常,您将通过 props 将信息从父组件传递到子组件。但是,如果必须将道具传递到中间的许多组件,或者应用中的许多组件需要相同的信息,则传递道具可能会变得冗长且不方便。Context 允许父组件将一些信息提供给其下树中的任何组件&am…...

「代码厨房大揭秘:Python性能优化的烹饪秘籍!」
哈喽,我是阿佑,上篇咱们讲了 Socket 编程 —— 探索Python Socket编程,赋予你的网络应用隐形斗篷般的超能力!从基础到实战,构建安全的聊天室和HTTP服务器,成为网络世界的守护者。加入我们,一起揭…...

【重学C语言】十六、联合、枚举、面向对象编程
【重学C语言】十六、联合、枚举、面向对象编程 联合定义联合体使用联合体注意事项枚举枚举的定义为枚举常量指定整数值枚举的使用枚举的打印枚举的优势注意事项面向对象编程1. 结构体(Structs)2. 封装(Encapsulation)3. 继承(Inheritance)...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
