算法训练 | 二叉树Part1 | 递归遍历、迭代遍历、统一迭代
目录
递归遍历
前序遍历
迭代遍历
前序遍历(迭代法)
中序遍历(迭代法)
后序遍历(迭代法)
统一迭代法
统一迭代
嵌入式学习分享个人主页:Orion嵌入式随想录 - 小红书 (xiaohongshu.com)
递归遍历
-
144.二叉树的前序遍历(opens new window)
-
94.二叉树的中序遍历
-
145.二叉树的后序遍历(opens new window)
-
文章讲解:代码随想录
前序遍历
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
-
解题思路
-
确定递归函数的参数和返回值:因为要打印出前序遍历节点的数值,所以参数里需要传入vector来放节点的数值,除了这一点就不需要再处理什么数据了也不需要有返回值,所以递归函数返回类型就是void,代码如下:
-
void traversal(TreeNode* cur, vector<int>& vec) -
确定终止条件:在递归的过程中,如何算是递归结束了呢,当然是当前遍历的节点是空了,那么本层递归就要结束了,所以如果当前遍历的这个节点是空,就直接return,代码如下:
-
if (cur == NULL) return; -
确定单层递归的逻辑:前序遍历是中左右的循序,所以在单层递归的逻辑,是要先取中节点的数值,代码如下:
-
vec.push_back(cur->val); // 中 traversal(cur->left, vec); // 左 traversal(cur->right, vec); // 右
-
-
代码注意
-
if (cur == NULL) return;终止条件 -
cur->val当前指针cur所指向的对象的val成员变量的值
-
-
代码一:前序遍历
class Solution {
public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val); // 中traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};-
代码二:中序遍历
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左vec.push_back(cur->val); // 中traversal(cur->right, vec); // 右
}-
代码三:后序遍历
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右vec.push_back(cur->val); // 中
}迭代遍历
-
文章讲解:programmercarl.com
前序遍历(迭代法)
-
为什么可以用迭代法(非递归的方式)来实现二叉树的前后中序遍历呢?在栈与队列:匹配问题都是栈的强项 (opens new window)中提到了,递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。
-
解题思路
-
前序遍历是中左右,每次先处理的是中间节点,那么先将根节点放入栈中,然后将右孩子加入栈,再加入左孩子。
-
-
解题步骤
-
定义栈,存放节点
-
定义数组,存放结构
-
确定终止条件,根节点入栈
-
循环处理栈,栈不为空则,获取栈并弹出,获取不为空则按中左右顺序将值加入数组
-
-
代码一:前序遍历(迭代法)
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); // 中st.pop();result.push_back(node->val);if (node->right) st.push(node->right); // 右(空节点不入栈)if (node->left) st.push(node->left); // 左(空节点不入栈)}return result;}
};中序遍历(迭代法)
-
在迭代的过程中,有两个操作:
-
处理:将元素放进result数组中
-
访问:遍历节点
-
-
解题思路
-
前序遍历的顺序是中左右,先访问的元素是中间节点,要处理的元素也是中间节点,所以刚刚才能写出相对简洁的代码,因为要访问的元素和要处理的元素顺序是一致的,都是中间节点。
-
中序遍历是左中右,先访问的是二叉树顶部的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点(也就是在把节点的数值放进result数组中),这就造成了处理顺序和访问顺序是不一致的。
-
在使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。
-
-
解题步骤
-
定义栈,存放节点
-
定义数组,存放结构
-
定义指针,用于遍历
-
循环处理栈,指针、栈不为空则,存入栈并向左走,为空则弹出处理存入数组,再向右走
-
-
代码二:中序遍历(迭代法)
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点,访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left; // 左} else {cur = st.top(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)st.pop();result.push_back(cur->val); // 中cur = cur->right; // 右}}return result;}
};后序遍历(迭代法)
-
解题思路
-
先序遍历是中左右,后续遍历是左右中,只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中。
-
-
解题步骤
-
定义栈,存放节点
-
定义数组,存放结构
-
确定终止条件,根节点入栈
-
循环处理栈,栈不为空则,获取栈并弹出,获取不为空则按中右左顺序将值加入数组
-
反转数组为左右中顺序
-
-
代码三:后序遍历(迭代法)
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)if (node->right) st.push(node->right); // 空节点不入栈}reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了return result;}
};
统一迭代法
-
文章讲解:代码随想录
统一迭代
迭代法实现的先中后序,其实风格也不是那么统一,除了先序和后序,有关联,中序完全就是另一个风格了,一会用栈遍历,一会又用指针来遍历。
针对三种遍历方式,使用迭代法是可以写出统一风格的代码,将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
-
解题思路
-
将访问的节点直接加入到栈中,但如果是处理的节点则后面放入一个空节点, 这样只有空节点弹出的时候,才将下一个节点放进结果集。
-
-
代码一:中序遍历
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)st.push(node); // 添加中节点st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)} else { // 只有遇到空节点的时候,才将下一个节点放进结果集st.pop(); // 将空节点弹出node = st.top(); // 重新取出栈中元素st.pop();result.push_back(node->val); // 加入到结果集}}return result;}
};-
代码二:前序遍历
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();if (node->right) st.push(node->right); // 右if (node->left) st.push(node->left); // 左st.push(node); // 中st.push(NULL);} else {st.pop();node = st.top();st.pop();result.push_back(node->val);}}return result;}
};-
代码三:后序遍历
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();st.push(node); // 中st.push(NULL);if (node->right) st.push(node->right); // 右if (node->left) st.push(node->left); // 左} else {st.pop();node = st.top();st.pop();result.push_back(node->val);}}return result;}
};(说明:基于代码随想录课程学习,部分内容引用代码随想录文章)
相关文章:

算法训练 | 二叉树Part1 | 递归遍历、迭代遍历、统一迭代
目录 递归遍历 前序遍历 迭代遍历 前序遍历(迭代法) 中序遍历(迭代法) 后序遍历(迭代法) 统一迭代法 统一迭代 嵌入式学习分享个人主页:Orion嵌入式随想录 - 小红书 (xiaohongshu.com) …...
AcWing 2568:树链剖分 ← 线段树+DFS
【题目来源】https://www.acwing.com/problem/content/2570/【题目描述】 给定一棵树,树中包含 n 个节点(编号 1∼n),其中第 i 个节点的权值为 ai。 初始时,1 号节点为树的根节点。 现在要对该树进行 m 次操作…...
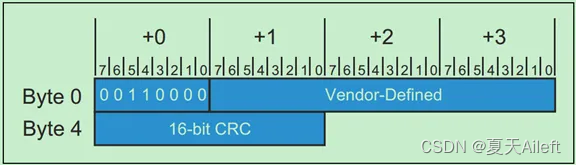
PCIe协议之-DLLP详解
✨前言: 🌟数据链路层的功能 数据链路层将从物理层中获得报文, 并将其传递给事务层; 同时接收事务层的报文, 并将其转发到物理层; 核心的功能有以下三点 1.保证TLP在 PCIe 链路中的正确传递; 2.数据链路层使用了容错…...
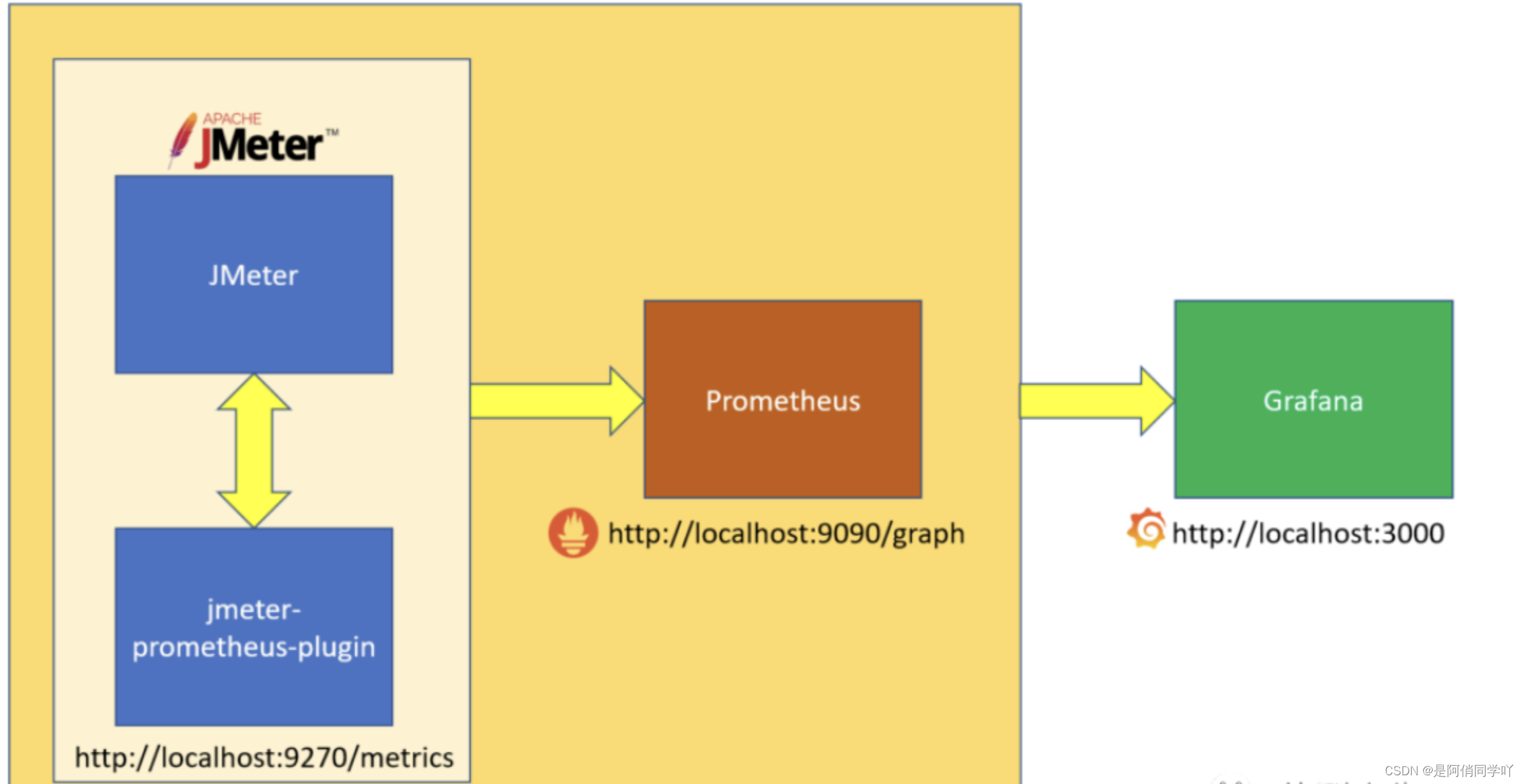
Jmeter+prometheus+grafana性能测试
文章目录 Jmeterprometheusgrafana性能测试背景目标设计思路原理案例启发 Jmeterprometheusgrafana性能测试 背景 在现代社会中,人们对于应用程序的响应速度和性能体验提出了越来越高的要求。无论是电子商务网站、社交媒体平台还是企业级软件系统,都…...
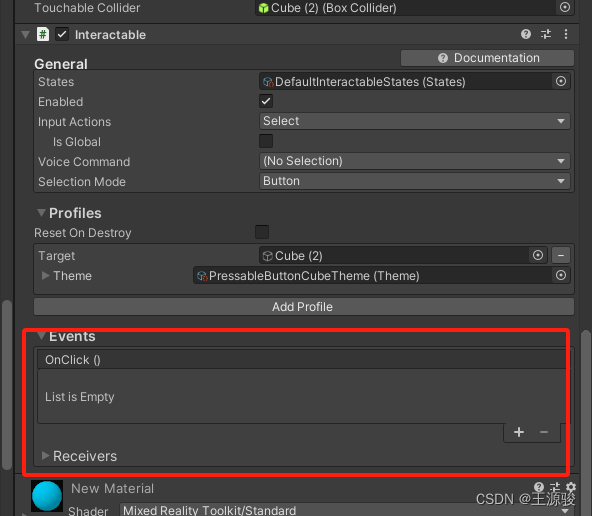
Hololens 2 新建自定义按钮
官方链接地址 1、创建Cube 2、添加PressableButton脚本,并点击AddNearin… 3、把Cube拖入到MovingButtonVisuals变量中 4、点击NearInteractionTouchable组件(这个组件是添加和上一个脚本绑定的,自动添加上来的)上的Fix… 5、…...

景源畅信:抖音小店新手小白如何做好运营?
在数字时代的浪潮中,抖音小店成为了众多创业者和商家的新宠。但面对激烈的市场竞争和不断变化的平台规则,新手小白如何才能在抖音小店的海洋里稳健航行,捕捉到属于自己的商机呢?接下来的内容将为你揭晓答案。 一、精准定位,明确目…...

力扣 42. 接雨水 python AC
双指针 class Solution:def trap(self, heights):l, r 0, len(heights) - 1maxl, maxr 0, 0ans 0while l < r:maxl, maxr max(maxl, heights[l]), max(maxr, heights[r])if maxl < maxr:ans maxl - heights[l]l 1else:ans maxr - heights[r]r - 1return ans单调栈…...

The 2022 ICPC Asia Nanjing Regional Contest - External D
G题 赛题补充 D题的题目来源 https://codeforces.com/gym/104128/problem/D 文章目录 题意思路代码 题意 给一个长度为n的数组,问对一段区间添加等差数列后的最大的第 k 大是多少 思路 通过观察题目可以发现答案的范围符合单调性,因此我们可以考虑二分…...

2024年蓝桥杯B组C++——复盘
1、握手问题 知识点:模拟 这道题很简单。但是不知道考试的时候有没有写错。一开始的43个人握手,仅需要两两握手,也就是从42个握手开始,而非43.很可惜。这道题没有拿稳这5分。也很有可能是这5分导致没有进决赛。 总结:…...
微调Llama3实现在线搜索引擎和RAG检索增强生成功能
视频中所出现的代码 Tavily SearchRAG 微调Llama3实现在线搜索引擎和RAG检索增强生成功能!打造自己的perplexity和GPTs!用PDF实现本地知识库_哔哩哔哩_bilibili 一.准备工作 1.安装环境 conda create --name unsloth_env python3.10 conda activate …...
【软件工程】【23.04】p1
关键字: 软件模型、提炼、加工表达工具、通信内聚、访问依赖、边界类交互分析、RUP核心工作流、首先测试数据流、软件验证过程、CMMI过程域分类工程类; 软件工程目的、功能需求是需求的主体、结构化方法、耦合、详细设计工具、类、类图、RUP采用用例技…...

Flutter 中的 ColoredBox 小部件:全面指南
Flutter 中的 ColoredBox 小部件:全面指南 在 Flutter 的世界中,ColoredBox 是一个用于填充颜色的简单而强大的小部件。它是一个不透明的矩形,可以用来创建颜色块,作为布局的占位符,或者简单地改变某个区域的背景色。…...

【LeetCode 随笔】面试经典 150 题【中等+困难】持续更新中。。。
文章目录 12.【中等】整数转罗马数字151.【中等】反转字符串中的单词6.【中等】Z 字形变换68.【困难】文本左右对齐167.【中等】两数之和 II - 输入有序数组 🌈你好呀!我是 山顶风景独好 💝欢迎来到我的博客,很高兴能够在这里和您…...

SwiftUI中AppStorage的介绍使用
在Swift中,AppStorage是SwiftUI中引入的一个属性包装器,在这之前我们要存储一些轻量级的数据采用UserDefaults进行存取。而AppStorage用于从UserDefaults中读取值,当值改变时,它会自动重新调用视图的body属性。也就是说࿰…...
iCloud 照片到 Android 指南:帮助您快速将照片从 iCloud 传输到安卓手机
概括 iOS 和 Android 之间的传输是一个复杂的老问题。将 iCloud 照片传输到 Android 似乎是不可能的。放心。现在的高科技已经解决了这个问题。尽管 Apple 和 Android 不提供传输工具,但您仍然有其他有用的选项。这篇文章与您分享了 5 个技巧。因此,…...

知识点总结
1、Uboot的流程调用: 1.1、cmd_process函数是怎么被调用到的: cmd_process在common/command.c 1.2、uboot阶段断电,后续起不来,可能要换线去使用,也许和电源线有关 2、git 相关使用 2.1 .gitignore相关的使用 1、…...

Python并发与异步编程
Python的并发与异步编程是两个不同的概念,但它们经常一起使用,以提高程序的性能和响应能力。以下是对这两个概念的详细讲解: 并发编程 (Concurrency) 并发编程是指在程序中同时执行多个任务的能力。Python提供了几种实现并发的机制ÿ…...
动态内存管理—C语言通讯录
目录 一,动态内存函数的介绍 1.1 malloc和free 1.2 calloc 1.3 realloc 1.4C/C程序的内存开辟 二,通讯录管理系统 动态内存函数的介绍 malloc free calloc realloc 一,动态内存函数的介绍 1.1 malloc和free void* malloc (…...
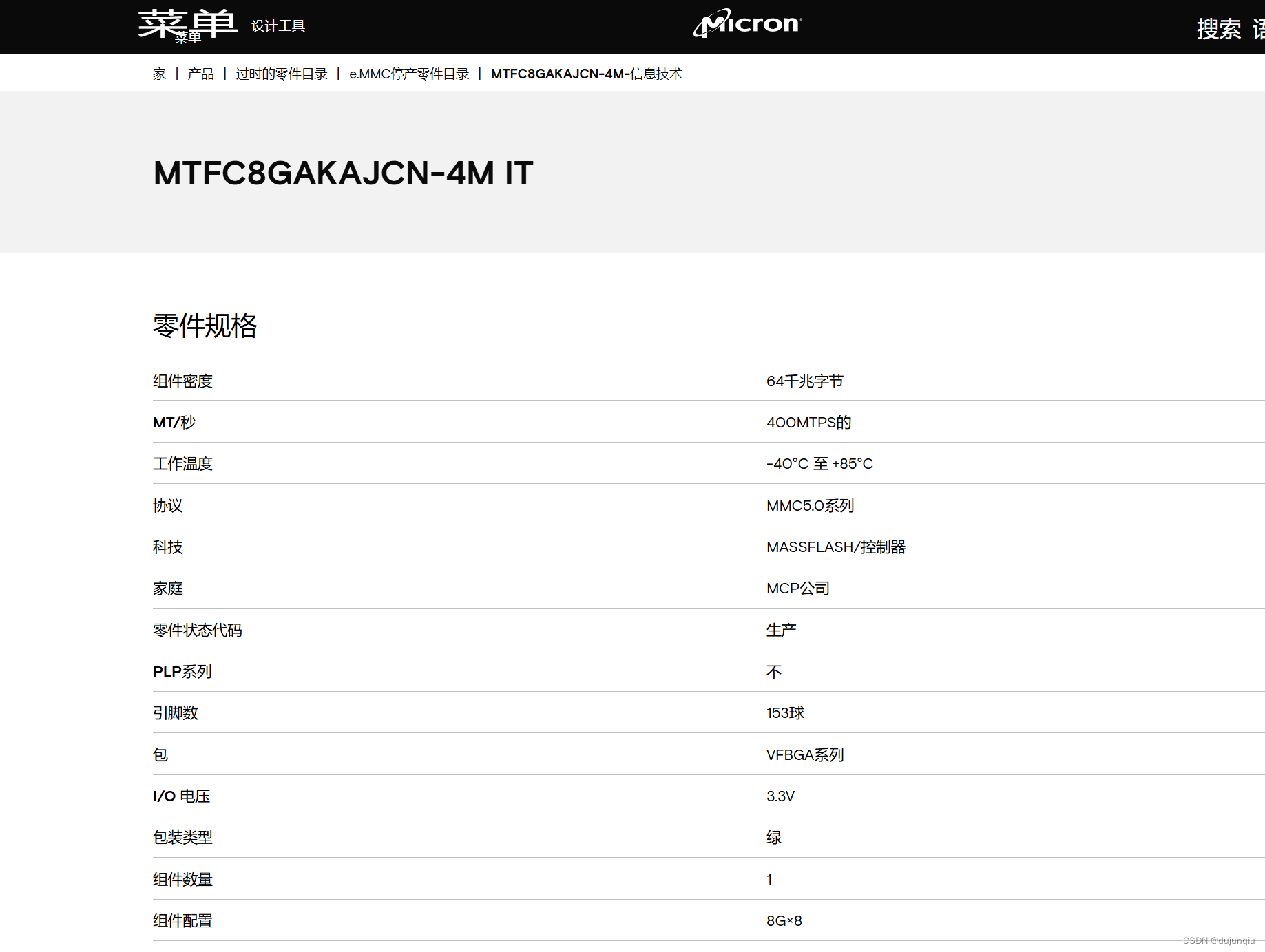
美光EMMC芯片丝印型号查询 8LK17/D9PSK, OXA17/JY997
问题说明 最近在使用美光EMMC的时候,发现通过芯片丝印查询不到 芯片的规格说明书; 经过查阅资料,发现美光的EMMC芯片 “由于空间限制,FBGA 封装组件具有与部件号不同的缩写部件标记”,需要通过官网查询丝印的FBGA cod…...

win32-鼠标消息、键盘消息、计时器消息、菜单资源
承接前文: win32窗口编程windows 开发基础win32-注册窗口类、创建窗口win32-显示窗口、消息循环、消息队列 本文目录 键盘消息键盘消息的分类WM_CHAR 字符消息 鼠标消息鼠标消息附带信息 定时器消息 WM_TIMER创建销毁定时器 菜单资源资源相关菜单资源使用命令消息的…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...
