赢球票问题
题目描述
某机构举办球票大奖赛。获奖选手有机会赢得若干张球票。
主持人拿出 N 张卡片(上面写着 1⋯N 的数字),打乱顺序,排成一个圆圈。
你可以从任意一张卡片开始顺时针数数: 1,2,3 ⋯⋯
如果数到的数字刚好和卡片上的数字相同,则把该卡片收入囊中,从下一个卡片重新数数。
直到再无法收获任何卡片,游戏结束。囊中卡片数字的和就是赢得球票的张数。
比如:
卡片排列是:1 2 3
我们从 1 号卡开始数,就把 1 号卡拿走。再从 2 号卡开始,但数的数字无法与卡片对上,很快数字越来越大,不可能再拿走卡片了。因此这次我们只赢得了 1 张球票。
还不算太坏!如果我们开始就傻傻地从 2 或 3 号卡片数起,那就一张卡片都拿不到了。
如果运气好,卡片排列是 2 1 3,那我们可以顺利拿到所有的卡片!
本题的目标:已知顺时针卡片序列,随便你从哪里开始数,求最多能赢多少张球票(就是收入囊中的卡片数字之和)
输入描述
第一行一个整数 N (≤100N≤100),表示卡片数目。
第二行 N 个整数,表示顺时针排列的卡片。
输出描述
输出一行,一个整数,表示最好情况下能赢得多少张球票。
输入输出样例
示例
输入
3
1 2 3
输出
1
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
#include<bits/stdc++.h>using namespace std;const int N = 1e2 + 10;int a[N],backup[N];int n = 0;int get(int k){int sum = 0, cnt = 1;//复制backup到a中 memcpy(a,backup,sizeof a);while(true){while(a[k]==0){//类似于循环队列 k = (k + 1) % n;}if(a[k]==cnt){sum+=a[k];a[k]=0;//重置判断数 cnt = 1;}else cnt+=1;k = (k + 1) % n;//第一种退出情况 if(cnt>n) return sum;//第二种退出情况: a[n]全为0 //if(*max_element(a,a+n)==0) return sum;int ss = 0;for(int i = 0;i < n ; i++){if(a[i]==0) ss++;}if(ss==n) return sum;}return -1;}int main(){cin>>n;for(int i = 0; i < n; i++){//backup备份数组 cin>>backup[i];}int ans = 0;//枚举所有开始位置 for(int i = 0; i <= n; i++){ans = max(ans,get(i));}cout<<ans<<endl;return 0;}
相关文章:

赢球票问题
题目描述 某机构举办球票大奖赛。获奖选手有机会赢得若干张球票。 主持人拿出 N 张卡片(上面写着 1⋯N 的数字),打乱顺序,排成一个圆圈。 你可以从任意一张卡片开始顺时针数数: 1,2,3 ⋯⋯ 如果数到的数字刚好和卡片上的数字相…...

Go语言基础之Error接口
Go语言基础之Error接口1.Error 接口2.创建错误3.fmt.Errorf1.Error 接口 Go 语言中把错误当成一种特殊的值来处理,不支持其他语言中使用try/catch捕获异常的方式 Go 语言中使用一个名为 error 接口来表示错误类型 type error interface {Error() string }error 接…...
Sqoop详解
目录 一、sqoop基本原理 1.1、何为Sqoop? 1.2、为什么需要用Sqoop? 1.3、关系图 1.4、架构图 二、Sqoop可用命令 2.1、公用参数:数据库连接 2.2、公用参数:import 2.3、公用参数:export 2.4、公用参数ÿ…...

C++ 之指针
文章目录参考描述指针运算符地址运算符奇偶分体指针的创建间接寻址运算符句点运算符运算符优先级问题箭头运算符运算符优先级指针野指针空指针通用指针解引用分析指针的算术运算加减运算自增运算与自减运算比较运算指针与常量指针常量常量指针指向常量的指针常量指针与数组数组…...

数据结构与算法---JS与栈
前言js里,是没有栈这种原生的数据结构。但是我们可以通过自定义创建栈类,来实现对添加/删除元素时更多的控制。创建栈类// 初始化一个基于数组的栈类 class Stack {constructor() {this.items [];} }为什么我们要选择数组作为栈类的存储数据类型&#x…...
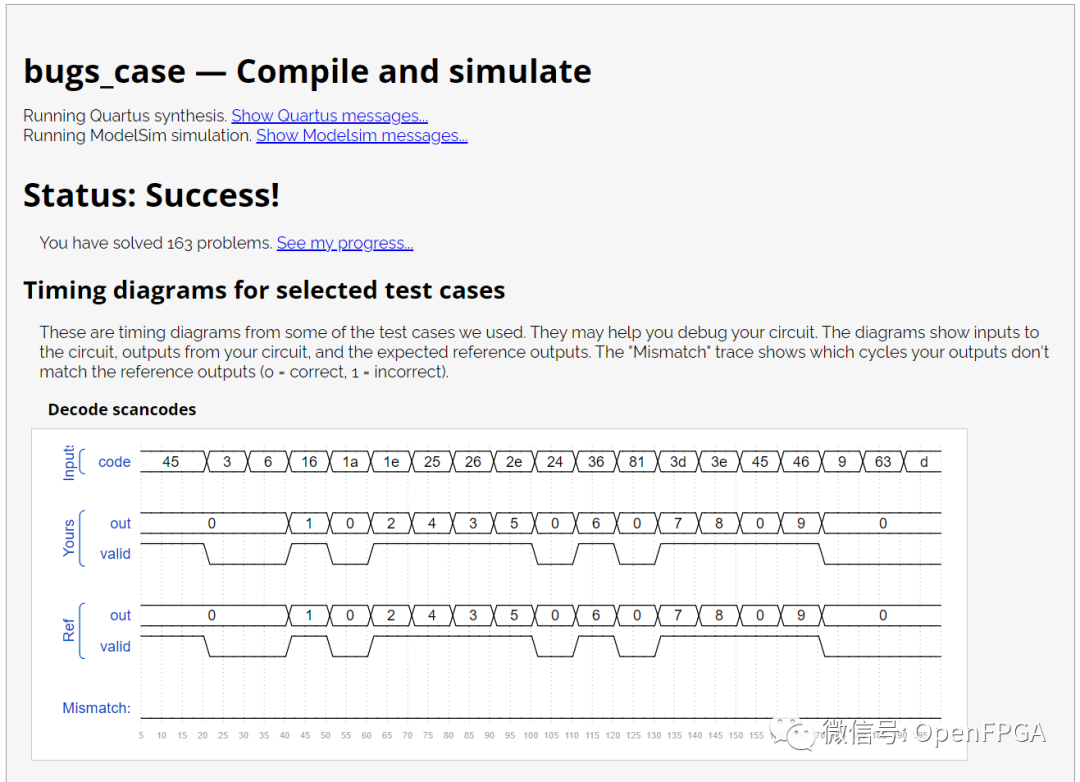
HDLBits: 在线学习 SystemVerilog(二十三)-Problem 158-162(找BUG)
HDLBits: 在线学习 SystemVerilog(二十三)-Problem 158-162(找BUG)HDLBits 是一组小型电路设计习题集,使用 Verilog/SystemVerilog 硬件描述语言 (HDL) 练习数字硬件设计~网址如下:https://hdlbits.01xz.ne…...

国外SEO升级攻略:如何应对搜索引擎算法变化?
搜索引擎优化(SEO)是一个动态的领域,搜索引擎的算法经常会发生变化,这意味着SEO专业人员需要保持更新的技术知识和策略, 以适应变化并提高网站的排名。 以下是一些应对搜索引擎算法变化的升级攻略: 创造…...

X.509证书
证书格式ASN.1是一种抽象的数据结构,描述了复杂的对象,以及对象之间的关系。证书本质上是一个文件,需要一种专门的格式,才能在互联网中传输,证书需要通过一个规则将ASN.1转换为二进制文件,这就需要对证书以…...

高等数学——微分方程
文章目录概念一阶微分方程可降阶的微分方程高阶线性微分方程线性微分方程解的结构常系数齐次线性微分方程常系数非齐次线性微分方程概念 微分方程:含有未知函数的导数或微分的方程称为微分方程。微分方程的阶:微分方程中所出现的未知函数最高阶导数的阶…...

JAVA小记-生成PDF文件
项目场景: 例如:项目中需要生成PDF文件 项目使用情况 1、引入pom.xml <!--pdf相关依赖--> <dependency><groupId>com.itextpdf</groupId><artifactId>itextpdf</artifactId><version>5.5.13</version> </dependency>…...
Noah-MP陆面过程模型建模方法与站点、区域模拟
陆表过程的主要研究内容以及陆面模型在生态水文研究中的地位和作用 熟悉模型的发展历程,常见模型及各自特点; Noah-MP模型的原理 Noah-MP模型所需的系统环境与编译环境的搭建方法您都了解吗?? linux系统操作环境您熟悉吗&…...

全国青少年软件编程(Scratch)等级考试一级真题——2019.9
青少年软件编程(Scratch)等级考试试卷(一级)分数:100 题数:37一、单选题(共25题,每题2分,共50分)1.小明在做一个采访的小动画,想让主持人角色说“大家好!”3秒…...
第十四届蓝桥杯三月真题刷题训练——第 6 天
目录 第 1 题:星期计算 问题描述 运行限制 代码: 第 2 题:考勤刷卡 问题描述 输入格式 输出格式 样例输入 样例输出 评测用例规模与约定 运行限制 代码: 第 3 题:卡片 问题描述 输入格式 输出格式 样…...

安装MySQL数据库8.0服务实例
前言 之前尝试去安装了MySQL5.7的社区版本,今天来安装MySQL8.0的版本,并且以两种方式进行安装,一个是通过RPM包的安装,另一个则是编译的方式。 一. 前期准备 查看服务器IP [rootlocalhost ~]# hostname -I 192.168.161.166 19…...
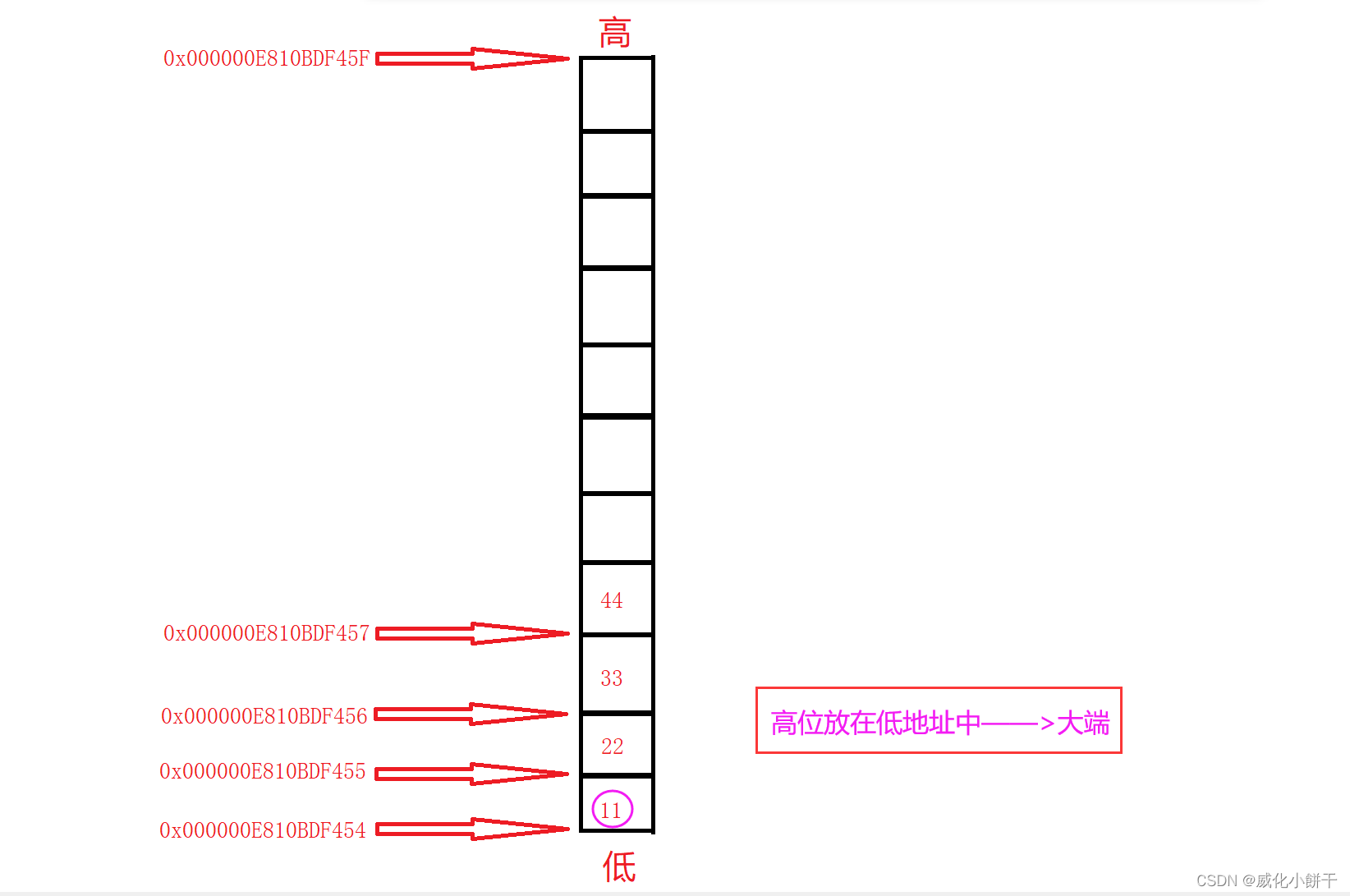
数据的存储--->【大小端字节序】(Big Endian)(Little Endian)
⛩️博主主页:威化小餅干📝系列专栏:【C语言】藏宝图🎏 ✨绳锯⽊断,⽔滴⽯穿!一个编程爱好者的学习记录!✨前言计算机硬件有两种存储数据的方式:大端字节序——Big Endian小端字节序——Little …...

软件测试备战近三银四--面试心得
自信即巅峰,对待面试官就像和儿子一样,耐心!耐心!耐心!...
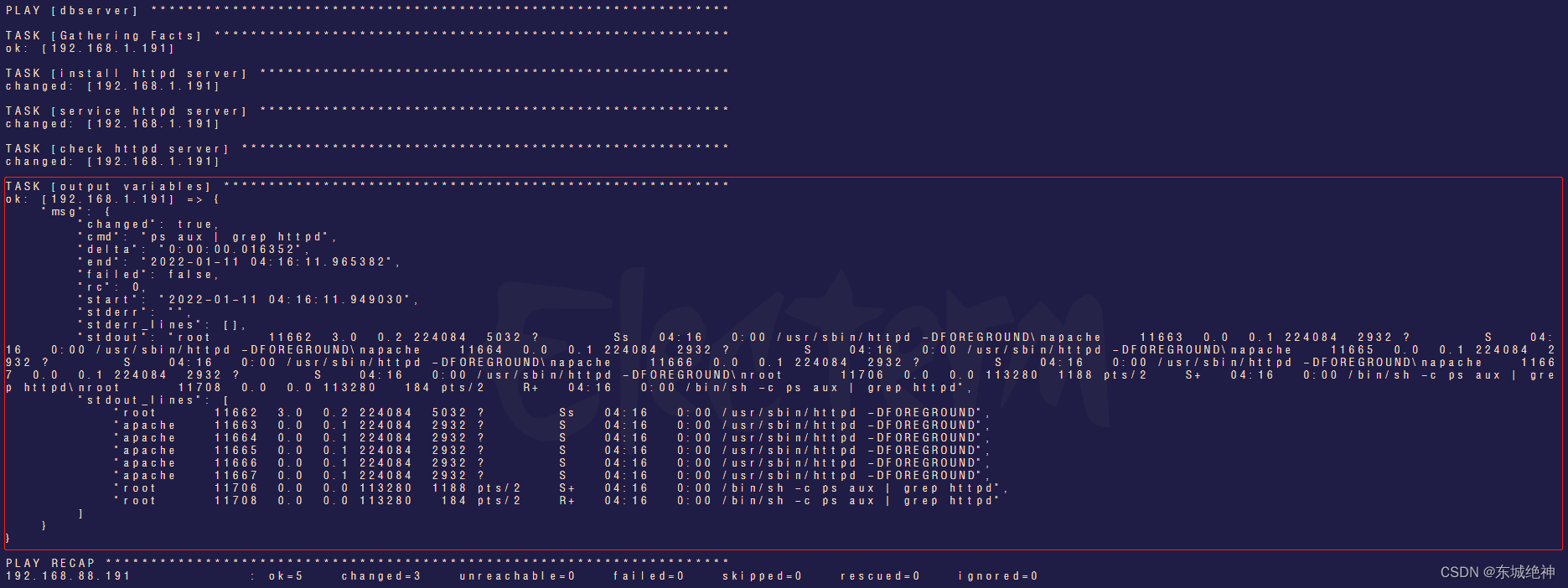
《Linux运维实战:ansible中的变量定义及以及变量的优先级》
一、配置文件优先级 Ansible配置以ini格式存储配置数据,在Ansible中⼏乎所有配置都可以通过Ansible的Playbook或环境变量来重新赋值。在运⾏Ansible命令时,命令将会按照以下顺序查找配置⽂件。 # ⾸先,Ansible命令会检查环境变量,…...
 监听 Form表单变化)
useEffect 通过 form.getFieldValue(‘xxx‘) 监听 Form表单变化
场景 子组件中,某一个表格的数据需要依赖于上级组件的某一个表单元素值进行计算。 毫无疑问,首先想到的肯定是监听 form 表单中元素的值,使用 useEffect 监听表单的变化,当值发生变化时,重新计算渲染。 首先说下我的…...
【晓龙oba出品 - 黑科技解题系列】- 最小操作次数使数组元素相等
思路 算法归根到底就是找规律的游戏,我们首先来看一个现象: 以数组nums [1,2,3,4,5]为例 当我们将数组排序后,可以知道最小值为1,最大值为5,此时我们需要四次运算可以使最小值与最大值相等: 第一次:2,3,4,…...
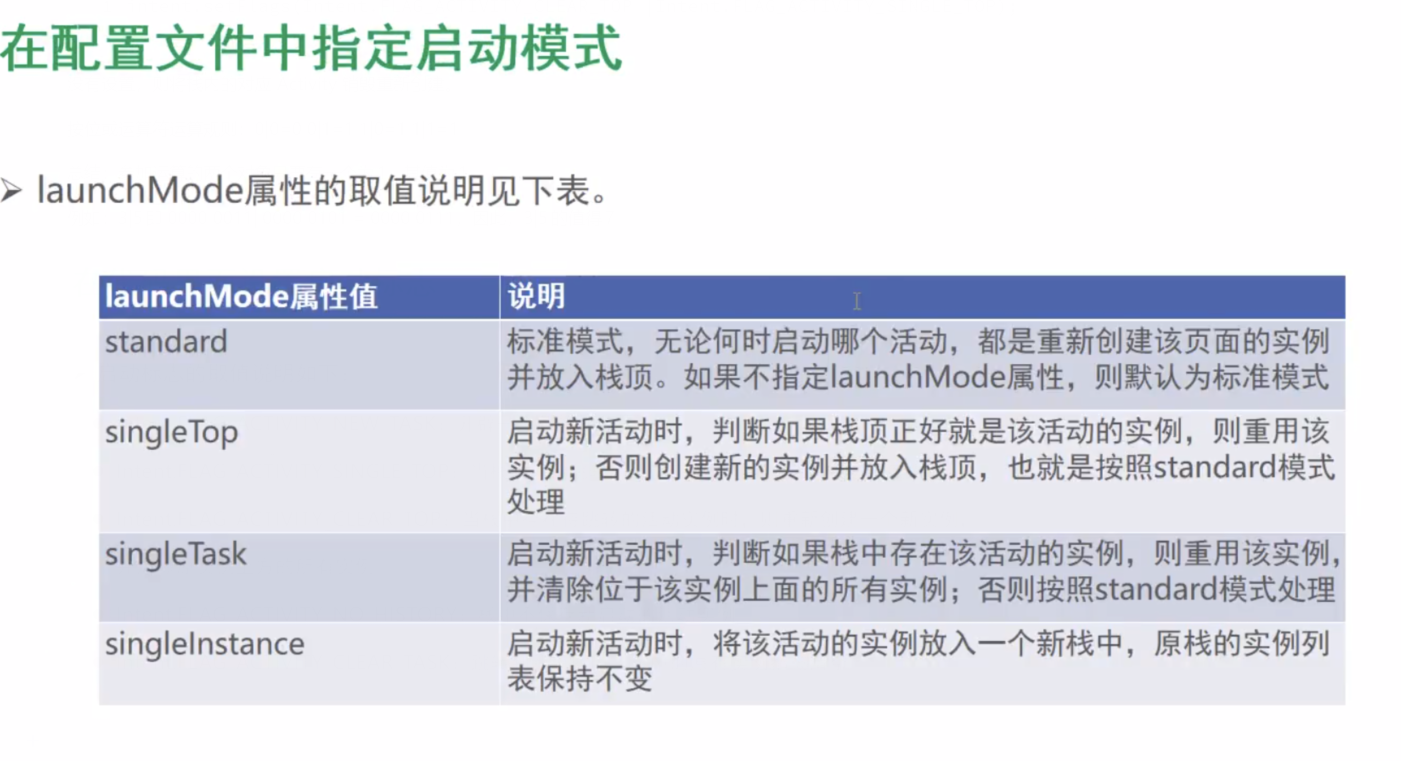
Activity的启动和结束
onCreate:创建活动。此时会把页面布局加载进内存,进入了初始状态。onStart:开启活动。此时会把活动页面显示在屏幕上,进入了就绪状态。onResume:恢复活动。此时活动页面进入活跃状态,能够与用户正常交互&am…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
