数据结构与算法---JS与栈
前言
js里,是没有栈这种原生的数据结构。但是我们可以通过自定义创建栈类,来实现对添加/删除元素时更多的控制。
创建栈类
// 初始化一个基于数组的栈类
class Stack {constructor() {this.items = [];}
}为什么我们要选择数组作为栈类的存储数据类型?
因为栈是一种遵从后进先出(LIFO)原则的有序集合。新添加或待删除的元素都保存在栈的同一端,称为栈顶,另外一端为栈底。在栈里,新元素越靠近栈顶,旧元素越靠近栈底。
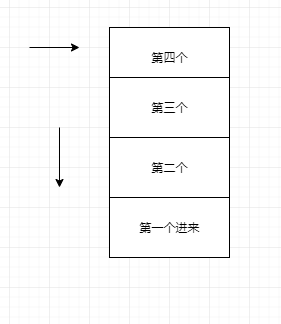
栈的用途很广。被用于编程语言的编译器和内存中保存变量、方法调用等。也用于浏览器历史记录(浏览器的前进后退)
对栈的设想
由于栈遵循LIFO原则,不像数组可以随意对数组内的元素进行操作。所以需要对元素的插入和删除等功能做限制。接下来,我们为栈类设想一些方法。
添加一个(或几个)新元素到栈顶
push(ele) {this.items.push(ele)
}移除栈顶的元素,同时返回被移除的元素
pop() {return this.items.pop();
}返回栈顶的元素,不对栈做任何修改
peek() {return this.items[this.items.length-1]
}如果栈为空则返回true 否则返回false
isEmpty() {return this.items.length === 0;
}移除栈内所有元素
clear() {this.items = [];
}返回栈里的元素个数
size() {return this.items.length
}实例化Stack类:
const stack = new Stack();
stack.isEmpty(); // true
stack.push(5);
stack.push(6);
stack.peek(); // 6创建一个基于JS对象的Stack类
作用
我们上面创建的Stack类,是使用一个数组来存储数据。那么我们现在为什么要用JS对象来替换Stack类的存储方式?
因为在使用数组时,大部分方法的时间复杂度为O(n)。n代表数组长度。即在最坏的情况下,我们需要迭代整个数组直到找到我们要找的那个元素。
另外数组是元素的一个有序集合,为了保证元素排列有序,它需要占用更多的内存空间。
在大多数编程语言里,能够直接获取元素,占用较少的内存空间的存储方式,无非是键值表了。
所以我们要使用一个JS对象来存储所有的栈元素,并保证他们的顺序并且遵循LFO原则。
声明一个Stack类
class Stack {constructor() {// count是预先索引,可以代表长度,但是不存在索引为count的元素this.count = 0;this.items = {};}
}为什么要定义count属性?为了记录栈的大小,并帮助我们添加或删除元素。
向栈中插入元素
要向栈中添加元素,我们将使用count变量作为items对象的键名,插入的元素则是它的值。在往栈插入元素后,我们递增count变量。
push(ele) {this.items[this.count] = ele;this.count ++;
}实例化栈
const stack = new Stack();
stack.push(5)
stack.push(8)
stack; // {count: 2,items:{0:5,1:8} }判断是否空栈和它的大小
size() {return this.count}
isEmpty() {return this.count === 0}从栈中弹出元素(从弹夹弹出最顶上的一颗子弹)
pop() {// 空栈,弹出undefinedif (this.isEmpty()) {return undefined;}this.count --;const result = this.items[this.count]delete this.items[this.count]return result
}查看栈顶的值
peek(){if (this.isEmpty()) {return undefined}return this.items[this.count - 1]
}清空栈
方法①一键还原
clear() {this.count = 0;this.items = {};
}方法②LIFO原则,循环出栈
clear() {while (!this.isEmpty()) {this.pop();}
}toString
当我们使用数组作为数据结构的时候,不需要关心toString的实现、而对象需要我们自己去定义。
var a =['a','b',5]
a.toString() // 'a,b,5'toString() {if (this.isEmpty()) {return ''};let objString = '';for (let i =0;i<this.count;i++) {objString+=(`[键名:${i}键值:${this.items[i]}]`)}return objString
}时间复杂度
除了toString方法,我们创建的其他方法的复杂度均为O(1);代表我们可以直接找到目标元素并对其操作.
保护JS栈类内部的数据结构
在栈设计中,我们希望保护内部的元素。只有我们暴露出的方法才能修改内部结构。
比如在栈中,我们要确保元素只能被添加到栈顶。而不是任意位置。
也就是说,我们需要保护Stack类中声明的items和count属性。
上面的例子中,无论是以数组或者对象作为存储的数据类型。items和count都是Stack类暴露出来的公开属性。
破坏Stack类
为了方便理解,我们以数组作为Stack类的存储数据类型。
const stack = new Stack();
stack.push(5);
console.log(Object.getOwnPropertyNames(stack)); // ['items']
// 或者
console.log(Object.keys(stack)) // ['items']
// 直接破坏数据属性
stack['items'] = [1,2,3];我们上面创建栈类是使用了ES6语法,是基于原型的类创建。这样做的好处在于能够节省内存空间并在扩展方面优于基于函数的类。但是这种方式不能声明私有属性的方法(直到ES11!)
保护内部属性-下划线命名约定
一部分开发者喜欢在js中使用下划线命名来约定这个属性为私有属性
class Stack {constructor() {this._items = {};this._count = 0;}
}
但这只是为了规范开发时对类属性的保护,实际上并没有用处。
保护内部属性 - ES6的限定作用域Symbol
出发的思路点就是为了躲避Object.getOwnPropertyNames和Object.keys对stack实例的属性扫描。
Symbol是ES6新增的一种基本数据类型。它是不可变的。可以用作对象属性。
const _ItemKey = Symbol('dataStack')
class Stack {constructor() {this[_ItemKey] = []}
}
var stack1 = new Stack()
Object.keys(stack1) // []
Object.getOwnPropertyNames(stack1) // []是不是找不到内部的_ItemKey属性了?
当你以为这样就可以成功躲避对象的属性扫描,那你就too young to simple啦
ES6新增的Object.getOwnProperty-Symbols方法能够拿到类里面声明的所有Symbols属性
Object.getOwnPropertySymbols(stack1) // [Symbol(stack01_item)]
stack1[Object.getOwnPropertySymbols(stack1)[0]] = [1,2,3]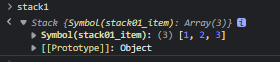
保护内部属性 - ES6的WeakMap
有一种数据类型可以确保属性是私有的,这就是WeakMap。WeakMap以键值对存储数据。
const db = new WeakMap()
class Stack {constructor() {db.set(this,[])}push(t) {const items = db.get(this);items.push(t)}pop() {const items = db.get(this);return items.pop()}
}
const stack2 = new Stack()
stack2.push(5)
stack2.push(10)
stack2 // {}
stack2.pop() // 10
Object.keys(stack2) // []
Object.getOwnPropertyNames(stack2) // []this是吧Stack类自己的引用作为键,存入WeakMap数据表里。
这样子确实是无懈可击了,Stack类里终于有了自己的私有属性。但是采用这种方法,会让代码变得难以理解,并且在继承扩展类时无法继承私有属性!
所以不推荐!
保护内部属性 - ES11的#变量
ES11(ES2020)在类中新增私有变量控制符#,在内部变量或者函数前添加一个hash符号#,可以将它们设置为私有属性,只能在类的内部可以使用。
class Stack {#items = {};#count = 0push(t) {this.#items[this.#count] = tthis.#count ++;}
}
const stack3 = new Stack()
stack3.push('ddd')
stack3.items; // undefined
stack3.#items // Uncaught SyntaxError: Private field '#items' must be declared in an enclosing class
Object.keys(stack3) // []用栈解决问题
栈可以解决很多计算机科学问题。
从十进制到二进制
在日常生活中,我们主要使用十进制,在计算机科学中,二进制非常重要。因为计算机的所有内容都是用二进制数字表示的(0和1)
我们要利用栈来强化JS把十进制转换成二进制的能力。
规则:
要把十进制转成二进制。我们可以用十进制数除以2(二进制是满二进一)并对商取整。直到结果是0为止。
我们现在把10转成二进制数字:

const decimalToBinary = (decNumber) => {const remStack = new Stack();let binaryString = '';// 避免方法改变传入的十进制值let cloneDecNumber = decNumber;while (cloneDecNumber > 0) {// 把余数存进去remStack.push(cloneDecNumber % 2);cloneDecNumber= Math.floor(cloneDecNumber /2);}// 取值while (!remStack.isEmpty()) {binaryString += remStack.pop().toString();}return binaryString
}decimalToBinary(233) // '11101001'
decimalToBinary(10) // '1010'
decimalToBinary(1000) // '1111101000'
decimalToBinary(100) // '1100100'进制转换算法
我们修改之前的算法。使它能够把十进制转换成基数为2-6的任意进制。
const baseConverter = (decNumber,base) => {const remStack = new Stack();let number = decNumber;let rem;let baseString = '';if (base <2 || base>36) {return ''}while (number > 0) {remStack.push(Math.floor(number % base))number = Math.floor(number / base)}// digits是参照表const digits = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'while (!remStack.isEmpty()) {baseString += digits[remStack.pop()];}return baseString
}
十进制转二进制,余数是0或1
十进制转为八进制,余数是0-7
十进制转十六进制时,余数是0-15(16-1),但是计算机语言里没有所谓的15,而是用A、B、C、D、E、F分别对应10、11、12、13、14、15
因此我们需要对栈中的数字做转化
从十一进制起,字母表中的每个字母代表对应的基数。
baseConverter (100345,2)
//'11000011111111001'
baseConverter (100345,8)
//'303771'
baseConverter (100345,35)
//'2BW0'
baseConverter (100345,16)
//'187F9'相关文章:

数据结构与算法---JS与栈
前言js里,是没有栈这种原生的数据结构。但是我们可以通过自定义创建栈类,来实现对添加/删除元素时更多的控制。创建栈类// 初始化一个基于数组的栈类 class Stack {constructor() {this.items [];} }为什么我们要选择数组作为栈类的存储数据类型&#x…...
HDLBits: 在线学习 SystemVerilog(二十三)-Problem 158-162(找BUG)
HDLBits: 在线学习 SystemVerilog(二十三)-Problem 158-162(找BUG)HDLBits 是一组小型电路设计习题集,使用 Verilog/SystemVerilog 硬件描述语言 (HDL) 练习数字硬件设计~网址如下:https://hdlbits.01xz.ne…...

国外SEO升级攻略:如何应对搜索引擎算法变化?
搜索引擎优化(SEO)是一个动态的领域,搜索引擎的算法经常会发生变化,这意味着SEO专业人员需要保持更新的技术知识和策略, 以适应变化并提高网站的排名。 以下是一些应对搜索引擎算法变化的升级攻略: 创造…...

X.509证书
证书格式ASN.1是一种抽象的数据结构,描述了复杂的对象,以及对象之间的关系。证书本质上是一个文件,需要一种专门的格式,才能在互联网中传输,证书需要通过一个规则将ASN.1转换为二进制文件,这就需要对证书以…...

高等数学——微分方程
文章目录概念一阶微分方程可降阶的微分方程高阶线性微分方程线性微分方程解的结构常系数齐次线性微分方程常系数非齐次线性微分方程概念 微分方程:含有未知函数的导数或微分的方程称为微分方程。微分方程的阶:微分方程中所出现的未知函数最高阶导数的阶…...

JAVA小记-生成PDF文件
项目场景: 例如:项目中需要生成PDF文件 项目使用情况 1、引入pom.xml <!--pdf相关依赖--> <dependency><groupId>com.itextpdf</groupId><artifactId>itextpdf</artifactId><version>5.5.13</version> </dependency>…...
Noah-MP陆面过程模型建模方法与站点、区域模拟
陆表过程的主要研究内容以及陆面模型在生态水文研究中的地位和作用 熟悉模型的发展历程,常见模型及各自特点; Noah-MP模型的原理 Noah-MP模型所需的系统环境与编译环境的搭建方法您都了解吗?? linux系统操作环境您熟悉吗&…...

全国青少年软件编程(Scratch)等级考试一级真题——2019.9
青少年软件编程(Scratch)等级考试试卷(一级)分数:100 题数:37一、单选题(共25题,每题2分,共50分)1.小明在做一个采访的小动画,想让主持人角色说“大家好!”3秒…...
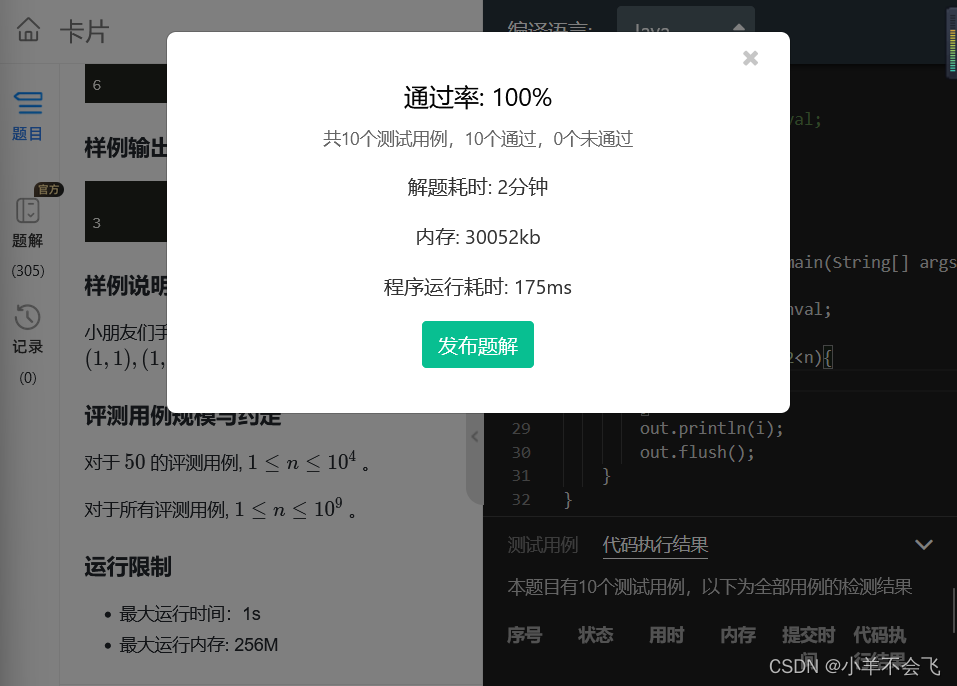
第十四届蓝桥杯三月真题刷题训练——第 6 天
目录 第 1 题:星期计算 问题描述 运行限制 代码: 第 2 题:考勤刷卡 问题描述 输入格式 输出格式 样例输入 样例输出 评测用例规模与约定 运行限制 代码: 第 3 题:卡片 问题描述 输入格式 输出格式 样…...

安装MySQL数据库8.0服务实例
前言 之前尝试去安装了MySQL5.7的社区版本,今天来安装MySQL8.0的版本,并且以两种方式进行安装,一个是通过RPM包的安装,另一个则是编译的方式。 一. 前期准备 查看服务器IP [rootlocalhost ~]# hostname -I 192.168.161.166 19…...
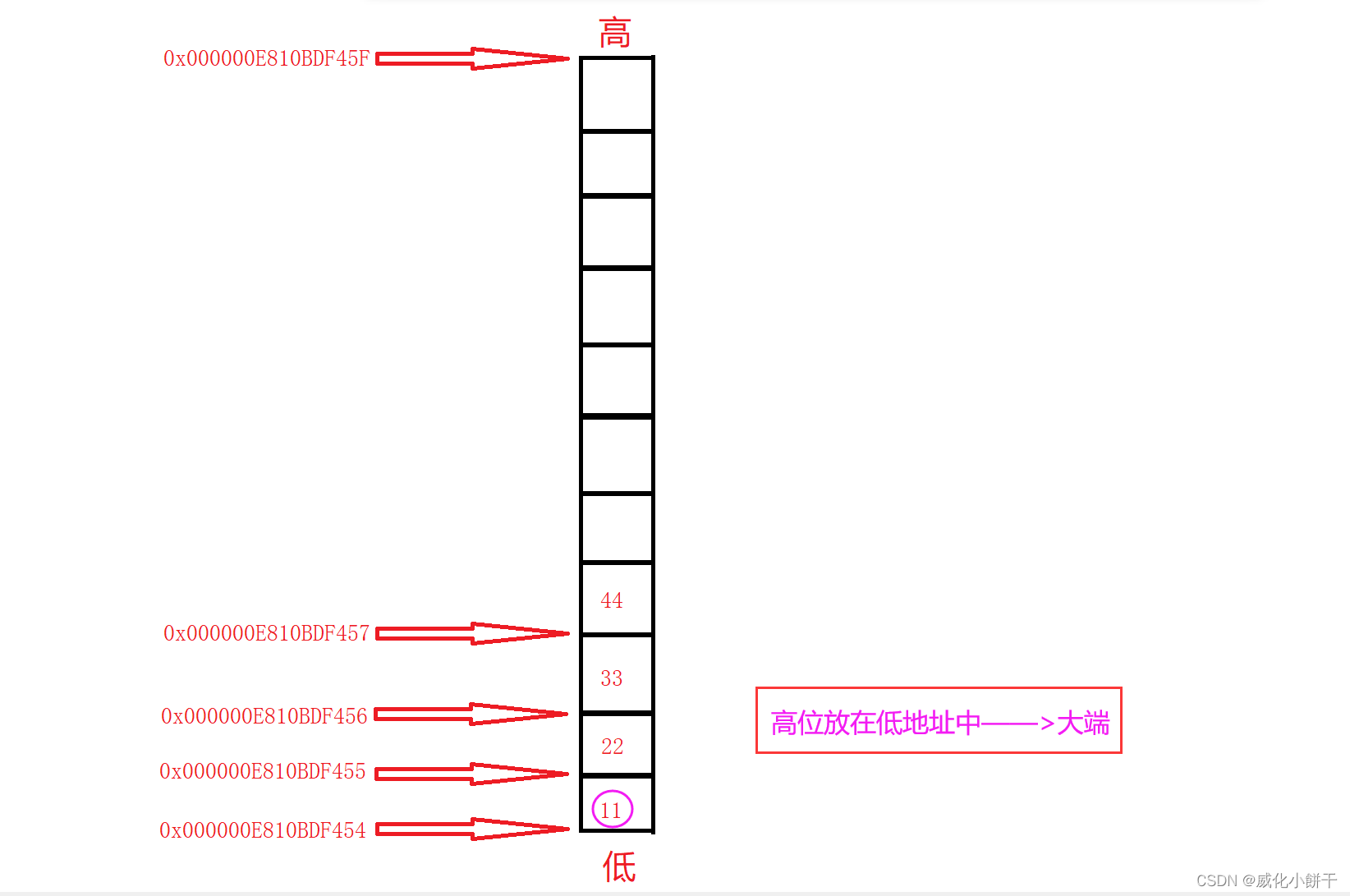
数据的存储--->【大小端字节序】(Big Endian)(Little Endian)
⛩️博主主页:威化小餅干📝系列专栏:【C语言】藏宝图🎏 ✨绳锯⽊断,⽔滴⽯穿!一个编程爱好者的学习记录!✨前言计算机硬件有两种存储数据的方式:大端字节序——Big Endian小端字节序——Little …...

软件测试备战近三银四--面试心得
自信即巅峰,对待面试官就像和儿子一样,耐心!耐心!耐心!...
《Linux运维实战:ansible中的变量定义及以及变量的优先级》
一、配置文件优先级 Ansible配置以ini格式存储配置数据,在Ansible中⼏乎所有配置都可以通过Ansible的Playbook或环境变量来重新赋值。在运⾏Ansible命令时,命令将会按照以下顺序查找配置⽂件。 # ⾸先,Ansible命令会检查环境变量,…...
 监听 Form表单变化)
useEffect 通过 form.getFieldValue(‘xxx‘) 监听 Form表单变化
场景 子组件中,某一个表格的数据需要依赖于上级组件的某一个表单元素值进行计算。 毫无疑问,首先想到的肯定是监听 form 表单中元素的值,使用 useEffect 监听表单的变化,当值发生变化时,重新计算渲染。 首先说下我的…...
【晓龙oba出品 - 黑科技解题系列】- 最小操作次数使数组元素相等
思路 算法归根到底就是找规律的游戏,我们首先来看一个现象: 以数组nums [1,2,3,4,5]为例 当我们将数组排序后,可以知道最小值为1,最大值为5,此时我们需要四次运算可以使最小值与最大值相等: 第一次:2,3,4,…...
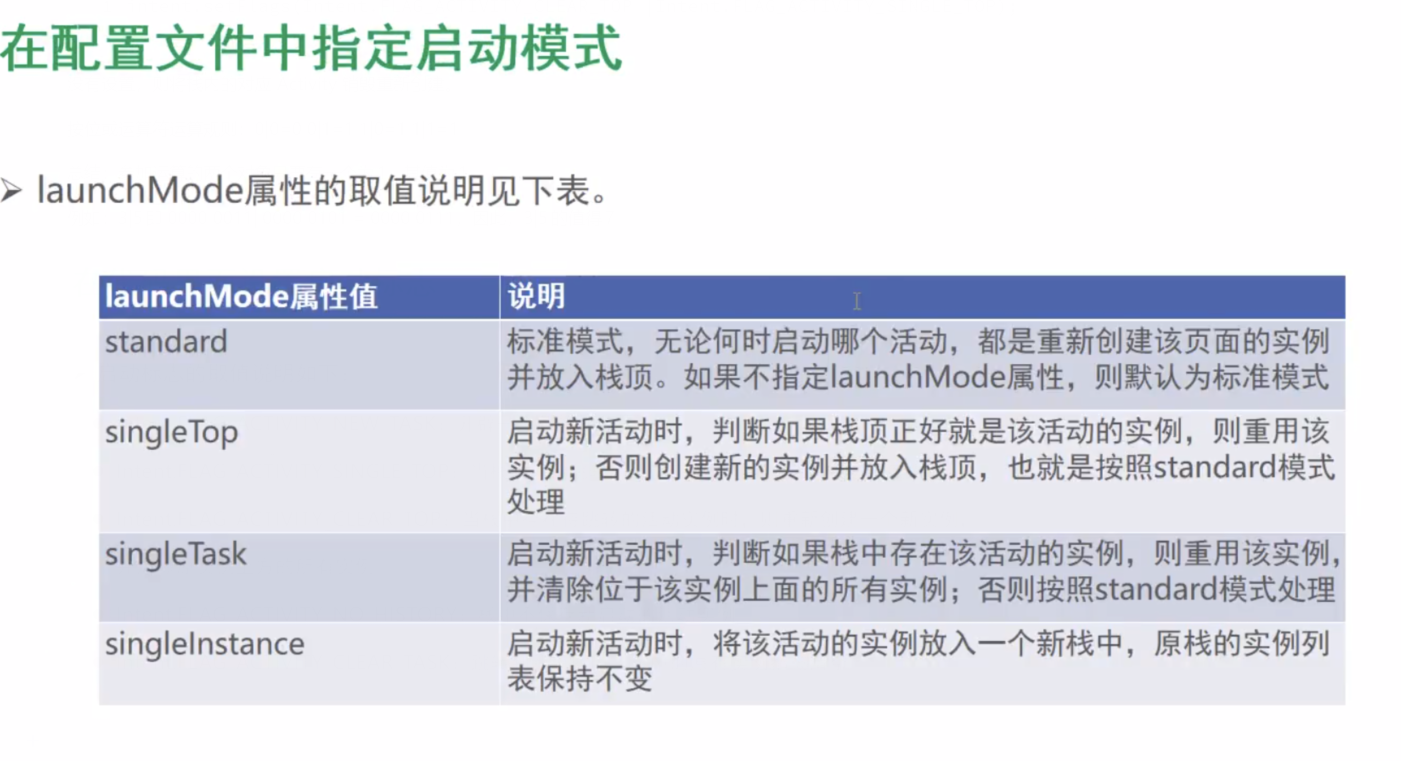
Activity的启动和结束
onCreate:创建活动。此时会把页面布局加载进内存,进入了初始状态。onStart:开启活动。此时会把活动页面显示在屏幕上,进入了就绪状态。onResume:恢复活动。此时活动页面进入活跃状态,能够与用户正常交互&am…...

利用业务逻辑+OB分布式特性优化SQL
最近某人社局核心数据库上了OB,经常出现性能问题 某人社与我司合作多年,非常信任我司在数据库的专业能力,邀请我司过去看看能否提供帮助 与OB驻场工程师合作,抓取了一天的TOP SQL,跑得慢的SQL有几十条(注意只是某一天的…...

哈希表
文章目录什么是哈希问题引入哈希函数直接定址法除留余数法 (常用、重点)哈希冲突哈希冲突的解决方法闭散列开散列unordered_map && unordered_set 封装实现哈希的应用位图布隆过滤器哈希经典面试题哈希切分位图应用布隆过滤器什么是哈希 在上一…...
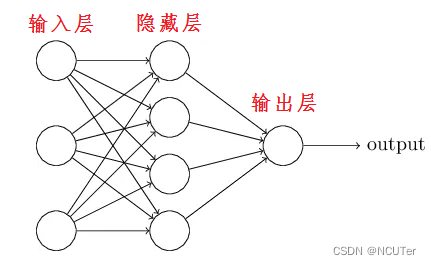
基于Halcon的MLP(多层感知神经网络)分类器分类操作实例
一、介绍 人工神经网络(Artificial Neural Network,ANN)简称神经网络(Neural Network,NN)或类神经网络,是一种模仿生物神经网络的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。 MLP神经网络是一种基于神经网络、动态的分类器。MLP分类器使用神经…...
VR全景博物馆,打造7*24小时的线上参访体验
导语:博物馆作为人们了解历史、文化和艺术的重要场所,现在可以通过VR全景技术来进行展览,让参观者身临其境地感受历史文化的魅力。本文将介绍博物馆VR全景的特点、优势,以及如何使用VR全景技术来丰富博物馆的展览和教育活动。什么…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
