AI学习指南数学工具篇-Python中的凸优化库
AI学习指南数学工具篇-Python中的凸优化库
在人工智能和机器学习领域,凸优化是一个非常重要的数学工具。它可以帮助我们解决各种问题,包括线性规划、二次规划、半定规划等。而在Python中,有一个非常优秀的凸优化库,即CVXPY。本文将为大家介绍CVXPY库的基本使用方法,并提供一些示例代码,帮助大家更好地理解和运用这一强大的数学工具。
CVXPY简介
CVXPY是一个用于凸优化建模和求解的Python库,它提供了简洁易用的API,可以帮助用户快速构建凸优化问题,并通过内置的优化器进行求解。CVXPY的设计理念是将凸优化问题的建模和求解过程分离,使用户能够专注于问题的建模,而不用过多关注求解的细节。
CVXPY的特点包括:
- 简洁的构建方式:通过Python的符号计算功能,用户可以使用直观的数学表达式来描述凸优化问题,而无需编写繁琐的求解算法。
- 多种内置优化器:CVXPY集成了多种常见的凸优化器,包括ECOS、SCS、OSQP等,可以满足不同问题的求解需求。
- 广泛的应用领域:CVXPY适用于各种凸优化问题,包括线性规划、二次规划、半定规划等,可以应用于机器学习、信号处理、控制系统等多个领域。
安装CVXPY
要使用CVXPY,首先需要安装该库。可以通过pip包管理器来进行安装:
pip install cvxpy
安装完成后,即可开始使用CVXPY进行凸优化建模和求解。
CVXPY的基本使用方法
CVXPY的使用方式非常简单,以下是一个简单的例子,演示了如何使用CVXPY来解决一个线性规划问题:
import cvxpy as cp# 定义问题的变量
x = cp.Variable()
y = cp.Variable()# 定义问题的约束条件
constraints = [x + y == 1, x >= 0, y >= 0]# 定义问题的目标函数
objective = cp.Minimize(x**2 + y**2)# 构建凸优化问题
problem = cp.Problem(objective, constraints)# 求解凸优化问题
problem.solve()# 打印结果
print("最优值:", problem.value)
print("最优解x:", x.value)
print("最优解y:", y.value)
在上面的例子中,我们首先定义了两个变量x和y,然后定义了约束条件和目标函数。接着,我们使用这些定义好的变量和函数来构建一个凸优化问题,并通过problem.solve()方法来求解该问题。最后,我们打印出了问题的最优值和最优解。
CVXPY示例:使用二次规划解决支持向量机问题
除了线性规划,CVXPY还可以用来解决其他类型的凸优化问题。下面我们将演示如何使用CVXPY来解决一个二次规划问题,以支持向量机(SVM)为例。
假设我们有一些训练数据 ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) (x_1, y_1), (x_2, y_2), ..., (x_n, y_n) (x1,y1),(x2,y2),...,(xn,yn),其中 x i x_i xi是输入数据, y i ∈ { − 1 , 1 } y_i \in \{-1, 1\} yi∈{−1,1}是对应的类别标签。我们的目标是找到一个最优的超平面,使得它能够最大化训练数据与超平面之间的间隔,并且保证所有数据点被正确分类。这个问题可以用二次规划的形式来描述:
min w , b , ξ 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i , i = 1 , 2 , . . . , n ξ i ≥ 0 , i = 1 , 2 , . . . , n \begin{equation} \begin{aligned} \min_{w, b, \xi} & \quad \frac{1}{2}||w||^2 + C\sum_{i=1}^{n}\xi_i \\ s.t. & \quad y_i(w^Tx_i + b) \geq 1 - \xi_i, \quad i = 1, 2, ..., n \\ & \quad \xi_i \geq 0, \quad i = 1, 2, ..., n \end{aligned} \end{equation} w,b,ξmins.t.21∣∣w∣∣2+Ci=1∑nξiyi(wTxi+b)≥1−ξi,i=1,2,...,nξi≥0,i=1,2,...,n
其中 w w w是超平面的法向量, b b b是偏置项, ξ i \xi_i ξi是松弛变量, C C C是正则化参数。
下面是使用CVXPY解决SVM问题的示例代码:
import numpy as np
import cvxpy as cp# 生成一些示例数据
np.random.seed(0)
X = np.random.randn(20, 2)
Y = np.sign(np.random.randn(20))
Y[Y==0]=-1# 定义问题的变量
w = cp.Variable(2)
b = cp.Variable()
xi = cp.Variable(20)# 定义问题的约束条件
constraints = [cp.multiply(Y, X@w+b) >= 1-xi, xi >= 0]# 定义问题的目标函数
C = 1
objective = cp.Minimize(0.5*cp.square(cp.norm(w)) + C * cp.sum(xi))# 构建凸优化问题
problem = cp.Problem(objective, constraints)# 求解凸优化问题
problem.solve()# 打印结果
print("最优超平面法向量w:", w.value)
print("最优偏置项b:", b.value)
在上面的代码中,我们首先生成了一些示例数据,然后定义了问题的变量、约束条件和目标函数。接着,我们使用这些定义好的变量和函数来构建一个凸优化问题,并通过problem.solve()方法来求解该问题。最后,我们打印出了问题的最优解,即最优的超平面法向量 w w w和偏置项 b b b。
结语
本文介绍了Python中的凸优化库CVXPY的基本使用方法,并通过实际的示例代码演示了如何使用CVXPY来解决线性规划和二次规划问题。希望本文能够帮助读者更好地理解CVXPY的功能和用法,从而更好地应用凸优化技术解决实际的问题。CVXPY作为一个强大而简洁的凸优化库,可以帮助我们更轻松地应对各种复杂的凸优化问题,是机器学习和人工智能领域不可或缺的重要工具。
相关文章:

AI学习指南数学工具篇-Python中的凸优化库
AI学习指南数学工具篇-Python中的凸优化库 在人工智能和机器学习领域,凸优化是一个非常重要的数学工具。它可以帮助我们解决各种问题,包括线性规划、二次规划、半定规划等。而在Python中,有一个非常优秀的凸优化库,即CVXPY。本文…...

数据库mysql
一、mysql常用语句 登录MySQLmysql -u root -p列出所有数据库SHOW DATABASES;创建一个新数据库CREATE DATABASE test;删除一个数据库DROP DATABASE test;对一个数据库进行操作时USE test;列出当前数据库的所有表SHOW TABLES;要查看一个表的结构DESC students;创建表CREATE TAB…...

AWS联网和内容分发之Transit Gateway
将Amazon VPC、AWS账户和本地网络连接到一个网关中。AWS Transit Gateway通过中央枢纽连接Amazon虚拟私有云(VPC)和本地网络。此连接简化了您的网络,并且结束了复杂的对等关系。Transit Gateway充当高度可扩展的云路由器,每个新的…...

牛客NC236 最大差值【simple 动态规划 Java/Go/PHP】
题目 题目链接: https://www.nowcoder.com/practice/a01abbdc52ba4d5f8777fb5dae91b204 思路 不难看出该题可以使用动态规划的方式解题。 在循环数组的过程中,记录截止到当前位置-1的最小值, 然后用当前的值去计算最大的差值。Java代码 im…...

ORACLE 6节点组成的ACFS文件系统异常的分析思路
近期遇到多次6节点集群的ACFS文件系统环境异常问题;如24日中午12点附近出现ACFS文件系统访问异常,通过查看集群ALERT日志、CSSD进程日志及OSW监控软件的日志,可以发现OSW监控软件在11:55-12:40分时没有收集到虚拟机LINUX主机的监控数据&#…...

vscode当前分支有未提交的修改,但是暂时不想提交,想要切换到另一个分支该怎么办
当前分支有未提交的修改,但是暂时不想提交,想要切换到另一个分支该怎么办? 首先,可以将当前修改暂存起来,以便之后恢复 git stash 然后切换到目标分支,例如需求A所在分支 git checkout feat-a-jie 修改完A需求后,需要先切换回之前的分支,例如需求B所在分支 git checkout feat…...

前端API: IntersectionObserver的那一二三件事
IntersectionObserver 基础 IntersectionObserver 可以监听一个元素和可视区域相交部分的比例,然后在可视比例达到某个阈值的时候触发回调。比如可以用来处理图片的懒加载等等 首先我们来看下基本的格式: const observer new IntersectionObserver(c…...

C++迈向精通:vector复现与sort复现
vector复现 思考过程 对于vector考虑如下几点: 底层数据结构算法实现方式对外表现形式 这里底层的数据结构采用了顺序表,当然,原版STL中的vector也是采用的顺序表。 算法实现的方式放在代码中去设计 对外表现形式是数组,因此需…...

【头歌】计算机网络DHCP服务器配置第二关access口配置答案
头歌计算机网络DHCP服务器配置第二关access口配置操作步骤 任务描述 本关任务:创建 vlan ,并且将与 pc 机相连接口划分 vlan 。 操作要求 在第一关的拓扑图的基础上,配置交换机,具体要求如下: 1、在特权模式下进入 vla…...
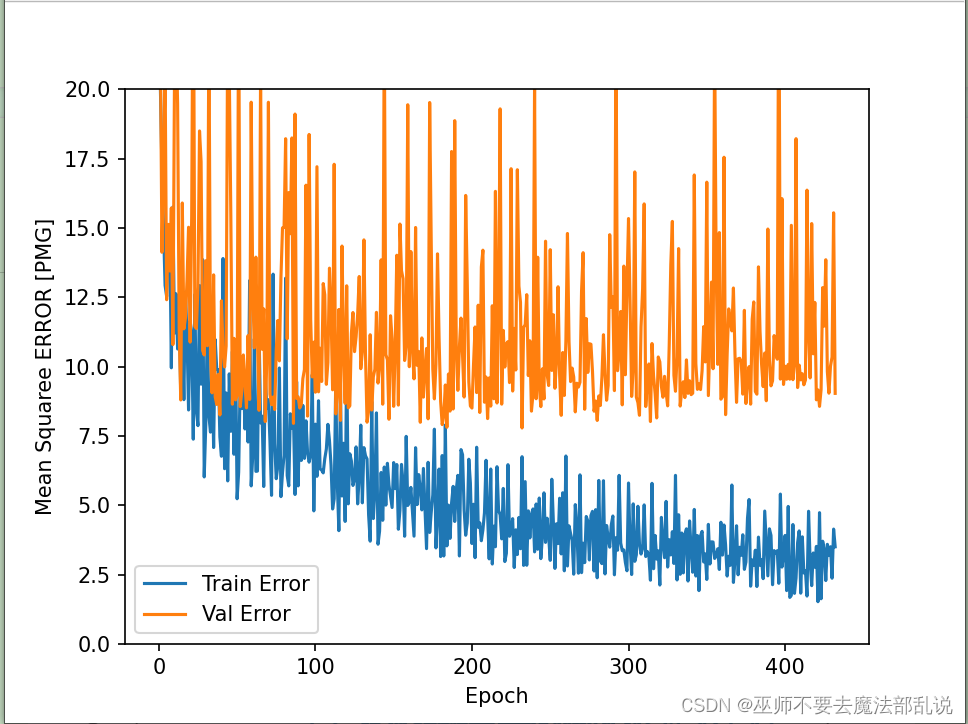
Python机器学习 Tensorflow + keras 实现CNN
一、实验目的 1. 了解SkLearn Tensorlow使用方法 2. 了解SkLearn keras使用方法 二、实验工具: 1. SkLearn 三、实验内容 (贴上源码及结果) 使用Tensorflow对半环形数据集分 #encoding:utf-8import numpy as npfrom sklearn.datasets i…...

基于事件的架构工作机制和相关产品
基于事件的架构 基于事件的架构可否这样理解,每个事件相当于传统API的一次函数调用请求,比如Add(123,456)。区别在于,基于事件的架构只是把这个请求发出,并不急于得到结果,而是等合适的子系统处理完这个请求ÿ…...
OSINT 与心理学:通过开源情报进行剖析和行为分析
在不断发展的心理学领域,人们越来越认识到通过应用开源情报 (OSINT) 方法取得进步的潜力。OSINT 主要以其在安全和情报领域的应用而闻名,并且越来越多地展示其在心理分析和行为分析方面的潜力。本文探讨了 OSINT 和心理学的迷人交叉点,研究如…...

yarn 设置淘宝镜像配置
为了提升在中国大陆地区的下载速度,你可以将Yarn的包仓库配置为淘宝镜像。最新的推荐做法是使用npmmirror.com作为镜像源,替代旧的npm.taobao.org。以下是设置Yarn使用淘宝镜像(npmmirror.com)的步骤: 查询当前镜像配置…...

debian 常用命令
Debian 是一个广泛使用的 Linux 发行版,这里列出了一些常用的 Debian 命令,适用于系统管理和日常使用: ### 文件与目录操作 1. **ls** - 列出目录内容: bash ls ls -l # 长格式显示 ls -a # 显示所有文件ÿ…...
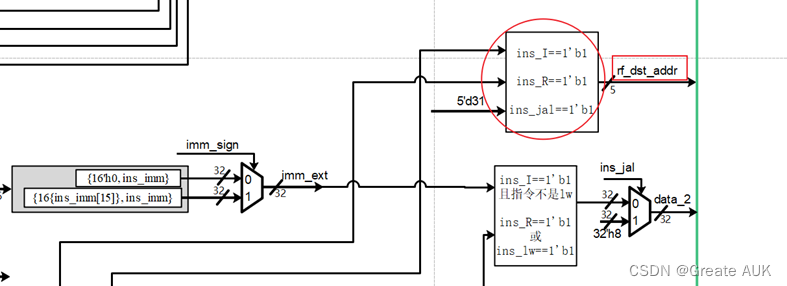
流水账(CPU设计实战)——lab3
Lab3 Rewrite V1.0 版本控制 版本描述V0V1.0相对V0变化: 修改了文件名,各阶段以_stage结尾(因为if是关键词,所以module名不能叫if,遂改为if_stage,为了统一命名,将所有module后缀加上_stage&a…...

k8s集群配置普通用户权限
集群管理员:负责管理 Kubernetes 集群的用户,拥有最高权限,可以对集群中的资源进行任何操作。 开发者:在 Kubernetes 集群中部署和管理自己的应用,可能有限制的权限,仅能管理特定的命名空间或资源。 第三…...

clickhouse——clickhouse单节点部署及基础命令介绍
clickhouse支持运行在主流的64位CPU架构的linux操作系统之上,可以通过源码编译,预编译压缩包,docker镜像和rpm等多种方式进行安装。 一、单节点部署 1、安装curl工具 yum install -y curl 2、添加clickhouse的yum镜像 curl -s https://pack…...
)
MATLAB基础应用精讲-【数模应用】价格敏感度PSM分析(附python代码实现)
目录 前言 算法原理 什么是价格敏感度分析? 原理 示例 PSM用途...

数据驱动的UI艺术:智能设计的视觉盛宴
数据驱动的UI艺术:智能设计的视觉盛宴 引言 在当今这个数据泛滥的时代,大数据不仅仅是一种技术手段,它更是一种艺术形式。当大数据遇上UI设计,两者的结合便催生了一种全新的艺术形式——数据驱动的UI艺术。本文将探讨如何将数据…...

栈的特性及代码实现(C语言)
目录 栈的定义 栈的结构选取 链式储存结构和顺序栈储存结构的差异 栈的代码实现 "stack.h" "stack.c" 总结 栈的定义 栈:栈是限定仅在表尾进行插入和删除操作的线性表。 我们把运行插入的和删除的一段叫做栈顶(TOPÿ…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
